图像相似度计算算法分析

王朝卿 沈小林 李磊

摘  要： 针对灰度直方图提取算法在计算图像相似度时，受颜色分布等外界因素干扰较大的问题，提出基于特征点匹配的SIFT算法。其可通过构建尺度空间提取特征关键点，求解匹配度来弥补传统算法在计算图像相似度时的局限性。实验结果表明，相比于传统算法，SIFT算法能够通过匹配更多的特征点，从而更好地计算图像的相似度;对于一组相似图片，通过SIFT算法能提取出308个特征点，图片相似度可达63%。

关键词： 图像识别; 图像相似度; 灰度直方图; 特征点匹配; 关键点; 尺度空间

中图分类号： TN911.73?34; TP391.4                  文献标识码： A                 文章编号： 1004?373X（2019）09?0031?04

Analysis on image similarity calculation algorithm

WANG Chaoqing1， SHEN Xiaolin1， LI Lei2

（1. School of Electrical and Control Engineering， North University of China， Taiyuan 030051， China;

2. School of Software Engineering， University of Science and Technology of China， Hefei 230000， China）

Abstract： A SIFT algorithm based on feature point matching is proposed to solve the problem that the gray histogram extraction algorithm is heavily disturbed by external factors such as color distribution while calculating image similarity. It can make up for the limitation of traditional algorithm in calculating image similarity by constructing scale space， extracting feature key points and solving matching degree. The experimental results show that， in comparison with the traditional algorithm， the SIFT algorithm can accurately calculate the image similarity by means of matching more feature points; can extract 308 feature points for a group of similar images， and the image similarity can reach up to 63%.

Keywords： image identification; image similarity; gray histogram; feature point matching; key point; scale space

0  引  言

隨着计算机技术的不断进步，图像识别技术也得到飞速发展，并广泛应用于国防科技、交通等领域中[1?3]。而图像相似度的计算是图像识别中的重要组成部分。

传统相似度计算方法根据图像生成的灰度直方图判断是否相似[4]，但存在受颜色分布等因素干扰明显的问题。本文采用特征点匹配算法[5]解决上述问题。因其实际应用广泛，诸多学者在相关理论研究中投入大量精力，并获得巨大成果。代表性的有Harris算法[6]、GLOH算法[7]和SIFT算法[8]等。通过实验采用传统算法与基于SIFT算法计算图像相似度并进行比较，分析两者优劣。

1  基于灰度直方图的图像相似度计算

基于灰度直方图的图像相似度计算过程简洁、执行效率高且不需对图像进行过多的预处理，已广泛应用于图像识别等领域。

1.1  灰度直方图

灰度直方图[9]反映出图像中出现不同灰度级像素的个数。若将图像总像素亮度（灰度级别）视为随机变量，则其分布情况就表示图像的统计特性。

假设任一图像中变量[r]为灰度级，对其作归一化处理后，[r∈[0，1]]且为随机变量。若[r]是连续的，则可用概率分布函数[P（r）]表示原始图像的灰度分布，直方图与[P（r）]相对应，概率密度函数[p（r）]则为直方图的累积和，也就是[p（r）]的积分，其公式分别如下：

1.2  余弦相似度

根据图像的灰度直方图，将图像转换为向量形式，通过两向量之间的余弦值计算图像的相似度[10]：

1.3  算法描述

具体算法过程如下：

1） 将两张图像大小调整为同样大小;

2） 获得两张图像的灰度直方图;

3） 将图像每4个灰度级划分成一个区，共64个区;

4） 对每个区的4个值进行求和运算，得到64个值，以此作为该图像的向量[11];

5） 計算两个向量的余弦相似度;

6） 判断图像的相似性。

2  基于特征点描述的图像相似度计算

2.1  SIFT算法

SIFT（Scale Invariant Feature Transform，尺度不变特征转换）用于描述影像中的局部特征。该算法可有效查找关键特征点，避免图形变换、光照和遮挡等因素影响。

SIFT图像匹配算法通过构建尺度空间，在该空间内检测局部极值点，消除偏移量过大的极值点及边缘响应，获得关键点，以此确定主方向，生成关键点描述子，并依据特征描述符向量进行匹配[5?12]。

2.2  算法描述

基于特征点匹配的SIFT算法步骤如下：

1） 构建尺度空间

① 构建高斯金字塔

高斯卷积核是实现尺度变换[13]的唯一线性核，一幅图像的尺度空间被定义为对其做可变尺度的高斯卷积：

对于灰度图像，利用不同大小的[σ]做高斯平滑。同时，将采样图像划分为不同组，每组有若干图像。一般情况下，上一组图像的长宽取下一组的2倍。

② 构建高斯差分金字塔

③ 极值点检测

将待检测图像与前后两张图像共26个邻域像素点的灰度值逐一比较，检测极值。

2） 关键点定位

离散空间的极值点并非真正的极值点，为提高关键点的稳定性，需拟合尺度空间函数。利用Taylor展开式求得极值偏移量。当任一维度的偏移量大于0.5时，改变当前关键点的位置，并在新的位置反复拟合直至收敛。若超出设定迭代次数或偏移量绝对值过小，存在不稳定点，可将该点视为非极值点。

此外，高斯差分函数的边缘效应[14]使特征点在某方向上有较大的曲率，而在垂直方向的主曲率很小，可将该点删除。

3） 方向分配

根据高斯差分金字塔中关键点的局部特性计算结果，可为每一点指定方向，使其具备旋转不变性。梯度模型和方向如下：

式中：[x，y]的正方向分别为右和上;[L]为关键点映射在尺度空间的灰度值;[m（x，y）]为梯度幅值;[θ（x，y）]为关键点所处梯度方向的弧度。按逆时针方向将360°依次划分为36个区域，获取不同方向的直方图。可按照[σ=1.5_octv]的高斯分布和[3σ]原则将[m（x，y）]加成，邻域窗口半径为3×1.5[σ][_]octv。

为增强算法鲁棒性，只保留峰值大于主方向峰值80%的方向为关键点的辅方向。完成上述过程，即获得SIFT特征点。

4） 关键点特征描述

在关键点尺度空间内4×4窗口中计算8个方向的梯度信息，共128维向量表征，即为关键点的描述子。具体步骤如下：

① 因划分的16个区域均为[3σ_octv]像素，则其半边长为[2×3σ_octv]，根据线性插值法，将半边长设为（4+1）×[3σ_octv2]。考虑到旋转因素，实际计算区域半径为：

② 坐标轴旋转至关键点方向[15]。

③ 计算三维坐标与邻域空间的距离，按距离的倒数求权重，并将梯度幅值按权重分配到邻域空间中。

④ 将128维向量归一化。同时，描述子按对应的高斯金字塔尺度大小排序。

5） 特征向量匹配

本文采用最近邻距离法匹配特征向量[16]。根据采样点与两个邻域点的特征向量，计算两者的欧氏距离之比，并同设定的阈值0.6进行比较。若比值小于该阈值，则认定特征向量匹配成功。

6） 相似度计算

计算匹配成功的特征点个数占图像中总特征点个数的百分比，即为图像的相似度。

3  实验结果分析

为验证两种算法计算图像相似度的效果，本文在PC机上编写Matlab程序，对两组图像进行相似度分析，如图1所示。其中图1a）和图1b）为相似图像，图1c）和图1d）为不同图像。

图1  实验图像

3.1  实验一

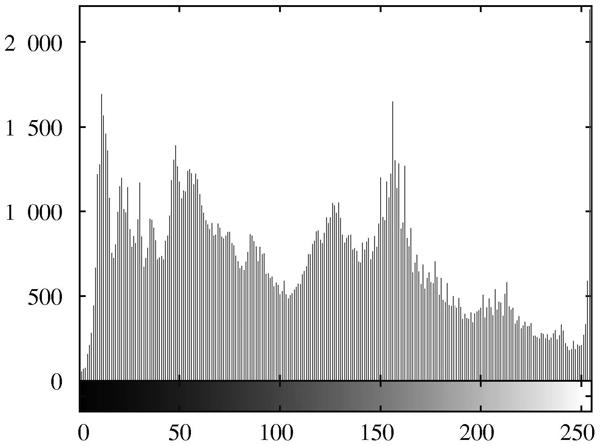
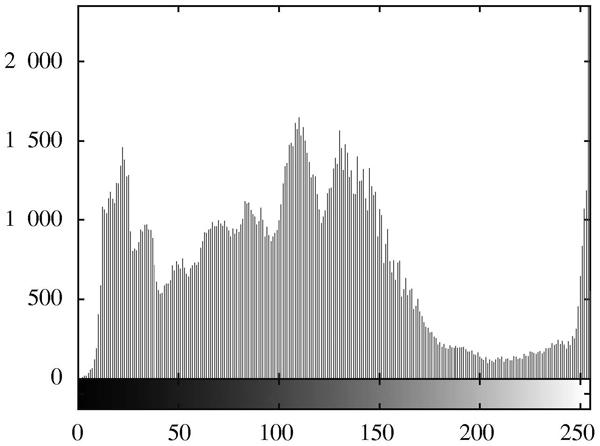
计算两组图像的灰度直方图如图2～图5所示。

通过灰度直方图可知，灰度值集中于前半部分，不难发现四张图像主要为暗色调，与肉眼观察一致。实验一的结果如表1所示。

实验结果表明，当颜色分布相差不大时，图像的灰度直方图较为接近。因此，利用该方法对颜色分布相近的不同图像进行相似度判断时存在误判。

图2  图1a）的灰度直方图

图3  图1b）的灰度直方图

图4  图1c）的灰度直方图