基于GA-BP神经网络的空气质量指数预测研究

吴慧静, 赫晓慧

(1.河南省农业科学院 经济作物研究所,河南 郑州 450002;2.郑州大学 智慧城市研究院,河南 郑州 450052)

近年来，随着城市的不断扩展，经济的快速发展以及人口的不断增长，城市环境问题越来越突出，也越来越受到广泛的关注。空气质量预报的发布能够为环保部门及时了解城市空气质量未来变化趋势提供科学依据[1]，对严重污染日及时作出预警，对大气污染采取限制措施，减轻对市民健康的危害，因此，建立空气质量预测模型对城市环境治理工作非常必要[2]。

目前，传统的空气质量预测方法包括数理统计、多元线性回归模型、时间序列、灰色系统等预测方法[3]。空气质量受天气因素、大气污染物的影响较大，具有明显的非线性、不确定特征，传统的预测方法很难得到有效的预测结果。神经网络可以建立复杂的非线性模型，从而能够更好的实现对空气质量的预测，是目前公认的最准确有效的监测方法之一。但是单一BP神经网络在搜索较大的解空间时，容易陷入局部最优，影响预测结果[4]。基于遗传算法改进的BP神经网络能够很好的解决此问题，预测结果具有更高的准确度和精度。

近年来，许昌市建成区面积不断扩大，市区人口不断增加，工业迅速发展，机动车数量快速增长，污染物排放量不断增大[5]，空气质量问题越来越突出。研究许昌市空气质量状况，建立许昌市空气质量预警预测模型，对许昌市污染防治工作具有重大的意义[6]。本文利用改进的神经网络，对许昌市空气质量指数AQI及空气质量等级进行预测，为城市环境综合治理和规划提供参考。

1 研究区概况

1.1 研究区概况

许昌市位于河南省中部，北距郑州80公里。东邻周口市，西交平顶山市，南界漯河市。介于东经113°03′～114°190′、北纬33°16′～34°24′之间。属暖温带季风区，气候温和，春季干旱多风沙，夏季炎热雨集中，秋季晴和日照长，冬季寒冷少雨雪，历年平均气温在14.3～14.6℃，平均降雨量在67.1～736.0mm。全境总面积4996平方公里，许昌市区建成区面积45.8平方公里，市区人口48万人。

2 数据来源与研究方法

2.2 空气质量分级标准

2012年上半年，国家出台《环境空气质量指数(AQI)技术规定(试行)》规定，将用空气质量指数(AQI)替代原有的空气污染指数(API)。AQI共分六级，从一级优，二级良，三级轻度污染，四级中度污染，直至五级重度污染，六级严重污染[7]。具体见表1。

2.1 数据来源

本文中研究数据来源于许昌市环境保护局，包括空气质量指数AQI日均值数据和天气数据。时间周期从2015年1月到2017年4月。天气数据包括天气状况、最低温度、最高温度、风速和风向日均值数据。经过剔除缺值日和无效数据，共计730d的日平均数据。

表1 空气质量指数级别和类别

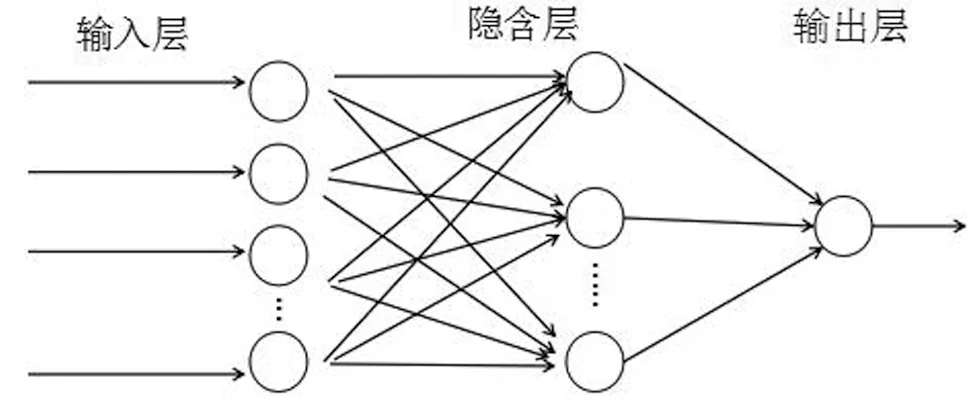
图1 三层BP神经网络模型Fig.1 The model of three layer BP neural network

2.3 神经网络

BP神经网络是基于BP算法的多层前馈网络，具有非线性动力学的特点。BP算法通过输入、输出数据样本集，根据误差反向传递的原理，对网络进行训练，其学习过程包括信息的正向传播过程以及误差的反向传播这两个过程，对其反复训练，连续不断地相对误差函数梯度下降的方向上，对网络权值和偏差的变化进行计算，逐渐逼近目标。典型的BP神经网络由一个输入层(多个输入值)、至少一个隐含层和一个输出层(多个输出值)组成。结构如图1所示。

需要说明的是激活函数包括S型函数和双曲正切函数两种，它们都是连续、单调递增的数值函数，只是值域的不同，前者的值域为(0，1)，后者的值域为(-1,1)。具体采用哪个函数需要根据输入/输出关系来确定。S型函数值域为(0，1)，适应于输出结果不含有负值的情况。本文研究的输出结果AQI不含有负值，所以可直接采用S型函数。基于此出发点，BP网络模型的主要算法简单描述如下：

(1)神经元采用激活函数

(1)

其中：x为函数输入。激活函数适用隐含层、输出层神经元。

计算模型隐含层连接权值的调整

(2)

由于

(3)

所以有

Δckl=Δdkjdkj(1-OMk)OIl

(4)

输出神经元阈值的调整可以表示为

(5)

其中：(0<β<1)令β=0.5。

计算阈值调整量：

(6)

2.4 遗传算法

遗传算法[8]起源于20世纪60年代,是模仿生物学和自然选择机理来建立的具有强大功能的算法，它是人工智能领域的一个重要分支，是通过构造优化搜索算法，来进行数学仿真，通常将它们运用到复杂的优化问题上，步骤如下[9]:(1)依据实际解空间的编码方式对初始群体进行编码；(2)计算出群体每个个体的适应值，并选择出适应度函数值大的个体进入下一代；(3)根据交叉率执行交叉操作；(4)根据变异率执行变异操作；(5)如果没有达到终止的条件，选择出适应度函数数值最大的个体作为问题的最优解。(6)进化完毕后，选择出适应度函数数值最大的个体作为问题的最优解。

2.5 遗传算法改进BP神经网络

BP神经网络算法容易陷入误差函数局部极小值，且收敛速度较慢，遗传算法具有全局搜索的功能[10]，因此，我们可以利用遗传算法优化BP神经网络的权值和阈值，将优化后的权值和阈值赋值给BP神经网络，训练BP神经网络预测模型获得最优解，发挥BP神经网络的局部搜索能力和全局搜索能力的优势。

3 预测仿真

3.1 数据预处理

本文采用的数据包括2015年1月—2017年4月的空气质量指数AQI日平均数据和同期气象数据，剔除缺值、无效值共有730天的数据。

同期的气象数据包括天气状况、温度、风力、风向等因子。部分原始气象数据见表2。

其中天气状况一共分为14种，包括晴、多云、阴、雾、小雨等。首先对气象原始数据中的天气状况进行数据数值化。天气状况数值化是从天气条件对AQI影响的角度考虑的，举例来说，在本研究中将“中雨/中雪/雨夹雪”对于AQI的影响视为等同，所以都数值化为4，其它数值化原理相同，具体设置见表3。

表2 部分原始气象数据

气象数据中的风向一共有九种，包括无持续风向、东风、西风、南风、北风等。对风向的数值化设置具体见表4。

表3 天气状况数值化

Table 3 Numerical simulation of weather conditions

数值天气状况1晴/多云2阴/雾3小雨/小雪4中雨/中雪/雨夹雪5阵雨/雷阵雨/大雨/暴雨/暴雪

气象数据中的风力根据等级大小，我们分为4类。风力较小时，对空气质量状况影响较小，因此，小于3级为一个等级。对于风力在5级以上的情况下，考虑两点，一是在许昌地区出现风力大于5级的情况在历史天气数据中并不多见，二是风力达到5级以上时，AQI均表现为优良天气，可以将风力对AQI的贡献视为等同。风力的具体数值化设置见表5。

表4 风向数值化

表5 风力数值化

对于数值化之后的气象数据，进行归一化处理，归一化后的数据分布在[-1,1]区间内。归一化后的部分数据见表6。

3.2 模型建立

空气污染物的积累和扩散受天气条件的影响，在污染源排放量无明显变化时，温度、气压、风速、降水等气象条件对城市空气质量有着重要的影响[11]。预测模型将污染物的排放量视为不变，考虑天气条件的变化对污染物的稀释扩散作用，根据当天天气预报的数据和前一天的空气质量数据，对当天的空气质量进行预测。

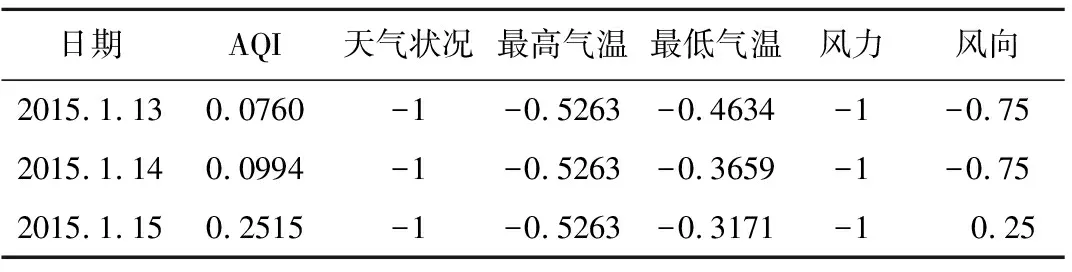
表6 数据归一化结果

本模型为预测当天的空气质量指数，利用前一天空气质量指数及当天天气状况(最低温度、最高温度、风向、风速和天气状况)建立模型。将前一天的空气质量指数和当天的天气预报数据作为神经网络的输入，将当天的空气质量指数作为神经网络的输出，用该模型对空气质量指数及空气质量等级进行预测。

预测模型的输入层设置为6维，分别为前一天AQI的值、当天天气状况、当天最高温度、当天最低温度、当天风速和当天风向。输出为1维，为当天AQI的值。隐含层的层数通过经验公式(见公式(7))和试错法确定，最终确定隐含层节点为4时，相对误差最小。经验公式如下：

(7)

其中，n为输入层节点数，m为输出层节点数，a为1～10之间的常数。最终确定的网络结构为6-4-1(见表7)。

根据确定的网络结构和初始权值和阈值进行实数编码，遗传算法的种群个体包含BP神经网络的权值和阈值，由前面确定的输入层R=6，S1=4，S2=1，根据公式：

S=R*S1+S1*S2+S1+S2

(8)

表7 BP神经网络网络结构

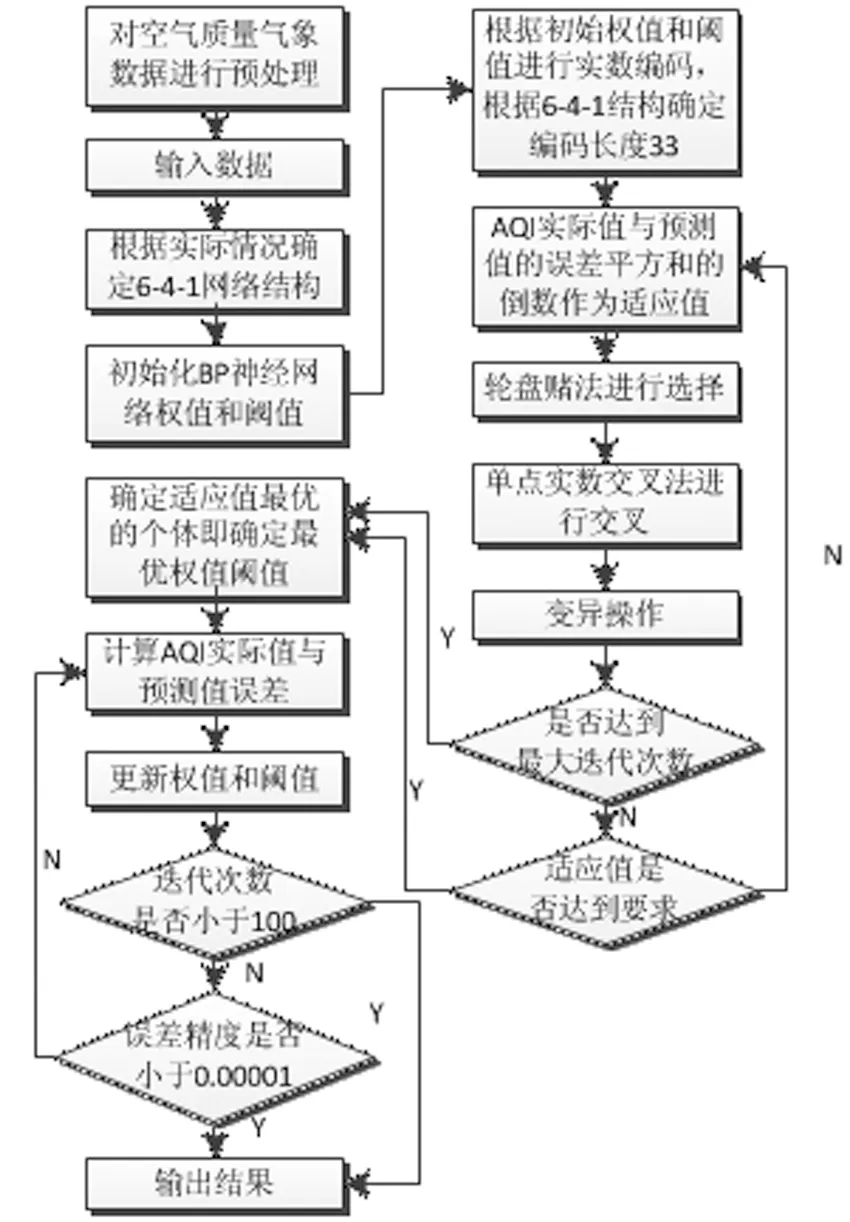
图2 GA-BP神经网络预测模型Fig.2 GA-BP neural network prediction model

计算出遗传算法的编码长度为33。将AQI实际值与预测值的误差平方和的倒数作为适应值，通过轮盘赌法进行选择，单点实数交叉法进行交叉，最后确定适应值最优的个体，即确定最优权值和阈值，计算出AQI实际值与预测值的误差。遗传算法的种群规模设置为100，进化次数设置为30次。变异概率为0.1，交叉概率为0.2。优化过程如图2所示。

3.3 结果分析

3.3.1 空气质量指数预测 首先通过rand()函数对730天的数据进行随机排序，随机选取650天的数据作训练样本，80天的数据作测试样本。在MATLAB 2014r进行预测仿真。结果见图3、图4。

从图3、图4可以看出，预测输出与期望输出的大致走势一致，但是存在一定的误差，为了更精确的评价预测结果，我们利用平均相对误差和准确率对预测结果进行评价，其中准确率的计算公式为

(9)

其中，Q为准确率，y1为预测输出，y2为期望输出。

空气质量指数预测结果对比分析见表8。

通过对比统计分析发现，在空气质量指数预测方面，BP神经网络平均相对误差为0.2452，GA-BP神经网络平均相对误差为0.2263，改进的BP神经网络平均相对误差低于单一的BP神经网络。改进的BP神经网络准确率为80.44%，相对于单一的BP神经网络，提高了4%。改进的BP神经网络在准确度方面优于单一的BP神经网络。

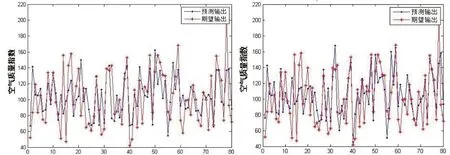
图3 优化前的输出 图4 优化后的输出 Fig.3 Output of before optimization Fig.4 Output of after optimization

为了更好地得知预测结果，根据预测结果，分别作出BP神经网络和优化后的BP神经网络的预测输出与期望输出的回归曲线，见图5、图6。这里需要说明的是，在训练数据不足或者维度特征过于复杂的情况下，会出现过拟合现象及欠拟合现象。本文的研究中，实验数据周期历时两年，有足够的训练数据，而且天气现象的属性维度只有最低温度、最高温度、风向、风速和天气状况等5个维度，训练过程和实验过程可以得到很好执行，所以不存在过拟合和欠拟合现象。

由表9可以看出，改进后的BP神经网络模型的预测输出与期望输出的相关度R为0.750，相对单一的神经网络具有更高的相关度，能够更好的预测空气质量指数的值，预测相对更准确。

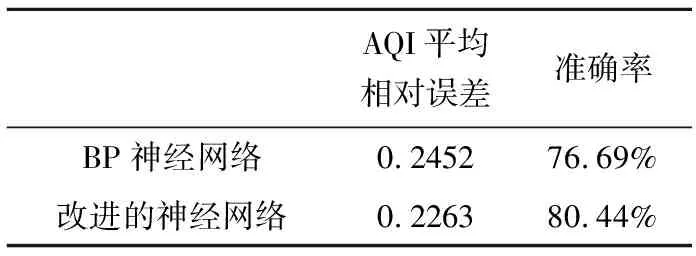
表8 空气质量指数预测结果对比分析

图5 BP神经网络拟合曲线 图6 GA-BP神经网络拟合曲线Fig.5 Fitting curve of BP neural network Fig.6 Fitting curve of BP neural network

3.3.2 空气质量等级预测 根据国家《环境空气质量指数(AQI)技术规定(试行)》，空气质量指数对应的级别标准参见表1。根据预测出的空气质量指数的值，可得相对应的预测出的空气质量等级。

根据已知的空气质量等级以及预测出的空气质量等级，作出空气质量等级期望输出和预测输出的曲线，见图7、图8、图9。由图7、图8和图9可见，改进的BP神经网络预测输出更接近于期望输出，BP神经网络预测输出相对误差较大，为了更好的了解预测结果，我们通过准确率来评价

预测结果。对空气质量等级预测结果进行计算和统计，BP神经网络在空气质量等级方面的预测准确率在78.75%，改进的BP神经网络预测值在82.5%，改进神经网络的预测结果与实际值的变化趋势大致相同，预测效果较好。

表9 拟合结果对比分析

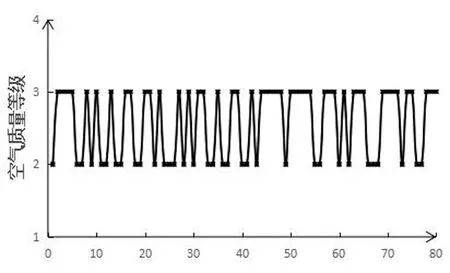
图7 空气质量等级期望输出

Fig.7 The desired output of air quality grade

图8 BP神经网络预测输出

Fig.8 The prediction output of BP neural network

图9 改进的BP神经网络预测输出

Fig.9 The prediction output of GA-BP neural network

4 结论与讨论

本文运用BP神经网络许昌市AQI的值进行了预测，通过输入当天的气象状况和前天的AQI的值，能够预测当天的AQI的值。单一的BP神经网络算法容易陷入误差函数局部极小值，利用遗传算法改进BP神经网络，能够解决单一BP神经网络的不足。结果表明，改进的BP神经网络预测模型对空气质量指数的预测准确度为80.44%，平均相对误差为0.2263，空气质量等级预测的准确率82.5%，均优于单一的BP神经网络的预测结果。

目前，国内外一些学者对空气质量预测作出研究[2,12-19]，例如，刘闵等人[2]通过逐步回归方法建立空气质量统计预报模型的空气质量级别准确率79.1%；江淑芳等人[12]建立的天气形势预测法，对深圳市空气质量进行预报，主要污染物的平均相对误差为20%-43%。本模型选择5个气象因子和1个基值作为输入，空气质量级别准确率80.44%，空气质量级别准确率82.5%。许杨等人[13]采用逐步线性回归法建立的预报模型对武汉市空气质量进行预测，预报准确率为78.1%。其他学者也对空气质量的预测作了一定的研究[14-19]。本文建立的空气质量指数预测模型，具有一定的参考价值和实用价值，可以将该模型应用到许昌市空气质量污染防治中，能够为许昌市空气质量的预报预警提供参考作用。

改进的BP神经网络在准确度方面相对于单一BP神经网络有所提高，但是AQI浓度的变化受多种因素的影响，本文建立的预测模型只考虑到气象因素对空气质量的影响作用，为了更加准确地对空气质量状况进行预测，还应该多考虑其他方面的因素，比如污染源排放，人类活动等因素。本文建立的预测模型有一定的参考意义，但预测的准确度有待进一步的研究和提高。