一类带积分边值条件的分数阶微分方程多个正解的存在性
2019-09-02周文学
孙 芮, 周文学
(兰州交通大学 数理学院,甘肃 兰州 730070)
分数阶微分方程起初是在1695年由Hospital和Leibniz提出的,近年来分数阶微积分受到了很多学者的广泛应用[1-6]。文献[5]在Riemann-Liouville导数的定义下利用Guo-Krasnosellskill不动点定理研究了分数阶微分方程边值问题
正解及其多个正解的存在性。其中f:[0,1]×R→R是一个非负连续函数。函数g:[0,1]→[0,),g∈L[0,1],存在W>0,W≠1使得g(s)sδ-1ds>W。且u(δ)(t)为一致分数阶导数,其定义由下文给出。
1 预备知识
记C([0,1],R)为定义在[0,1]→R上的连续实值函数构成的Banach空间,其范数为‖u‖=sup{|u(t)‖t∈[0,1]}。设Ck([0,1],R)为[0,1]→R上k次可微实值函数构成的Banach空间,其范数为‖u‖Ck=max{‖u‖,…,‖u(k)‖}。本文中Cδ([0,1],R)为定义在[0,1]→R上直到分数δ次连续可微实值函数构成的Banach空间,δ∈(2,3],其范数为‖u‖Cδ=max{‖u‖,…,‖u(δ)‖}。设LP([0,1],R)为定义在[0,1]→R上满足可测函数构成的Banach空间,其范数
定义1[3]设δ∈(n,n+1]且f:[0,]→R。f的一致分数阶导数可定义为
(1.1)
常用f(δ)表示,其中[δ]表示大于等于δ的最小整数。
定义2[3]设δ∈(n,n+1]且f:[0,]→R。f的一致分数δ次积分可定义为
(1.2)
特别地,在本文中δ∈(2,3],则
(1.3)
引理1[3]对任意的f∈C([0,1],R)。带积分边值条件的分数阶微分方程边值问题
(1.4)
有唯一解

(1.5)
其中
(1.6)
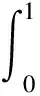
引理2由(1.6)式定义的Green函数G(t,s)具有以下性质
(1)对任意t,s∈(0,1),G(t,s)≥0;
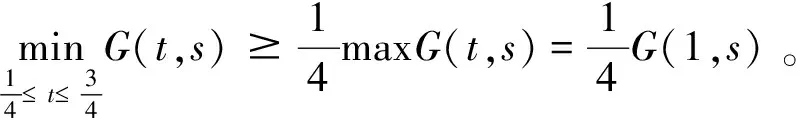
证明:(1)显然成立;下面证明(2),

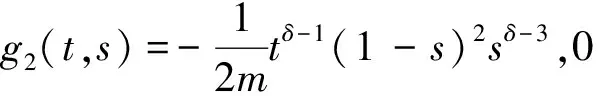
因为δ∈(2,3],0st1,显然G(t,s)≥0即g1(t,s)>0,g2(t,s)>0。

所以G(t,s)关于t是单调递增的。
注意到
下面我们证明:
(i)当0 显然, 引理3[7]若函数f∈C([0,1]×[0,),[0,)),则(1.4)式的唯一解u满足 证明:由(1.4)-(1.6)式知u可表示为 (1.7) 从而,我们有 结合引理1有 为方便起见,我们引入以下记号 则P是X上的锥。定义算子T:P→P: 由引理1,边值问题(1.4)-(1.6)有解u=u(t)当且仅当u是算子方程u=Tu的解。 (1)‖Tx‖‖x‖,x∈P∩∂Ω1,并且‖Tx‖≥‖x‖,x∈P∩∂Ω2; (2)‖Tx‖≥‖x‖,x∈P∩∂Ω1,并且‖Tx‖‖x‖,x∈P∩∂Ω2。 定理1假设函数f:[0,1]×[0,)→[0,)连续,存在正常数a,b,a≠b,使得: (H2)f(t,u)当(t,u)∈[0,1]×[0,b]时。 则边值问题至少存在一个正解u′使得min{a,b}‖u′‖max{a,b}。 证明:首先证明T:P→P全连续。 事实上,如果u∈P,根据G(t,s)与f(t,u)的非负性,当u∈P时,则有 (Tu)(t)≥0,0t1。 另一方面 根据引理1知: 因此,T:P→P。 又根据G(t,s)与f(t,u)的连续性,由Arzela-Ascoli定理,可知T是全连续的。设 Ω1={u∈X|‖u‖ 则Ω1,Ω2是X上的有界开集。 当u∈P∩∂Ω1时,由P的定义知 由(H1)我们得到, 因而u∈P∩∂Ω1时‖Tu‖≥‖u‖。 当u∈P∩∂Ω2时,由(H2)我们得到: 因而‖Tu‖‖u‖时,u∈P∩∂Ω2。 min{a,b}‖u′‖max{a,b}。 定理2假设函数f:[0,1]×[0,)→[0,)连续,满足下列之一: f(t,u) f(t,u) 则边值问题(1.4)-(1.6)至少有两个解。 f(t,u) 其中N>0,令Ωr={u∈C[0,1]|‖u‖ (Tu)|G(t,s)f(s,u(s))ds| =l=‖u‖。 因此,对任意的u∈P∩Ωr,‖Tu‖<‖u‖。 令Ωq={u∈C[0,1]|(t,u)∈[0,1]×[0,l]},对u∈p∩∂Ωq,我们有 因此,对任意的u∈P∩∂Ωq,‖Tu‖≥‖u‖。 0‖u1‖ 又由引理3知, 因此u∈P∩∂Ωr时有‖Tu‖‖u‖。 l‖u2‖。 0‖u1‖l‖u2‖。 且满足, 所以问题(1.4)-(1.6)至少有两个正解。 例1考虑分数阶微分边值问题 (3.1) (3.2) 其中0 又由于 f(t,u) 因此定理2结论成立。即边值问题(3.1)-(3.2)至少有两个正解u1,u2。 文章在阅读大量相关书籍和文献的基础上,探究一类具有积分边值问题的分数阶微分方程多个正解的存在性,获得了正解存在性定理和多个正解存在的判断依据,最后通过具体的例子验证了结论的适用性。








2 主要结果
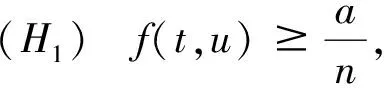

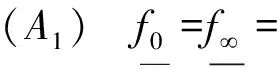

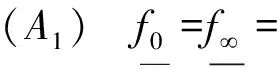





3 举 例

4 小 结
