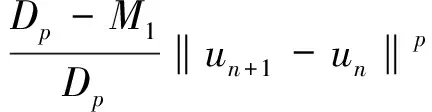一类拟线性椭圆方程解的存在性
2019-09-02高芳,陈林
高 芳, 陈 林
(伊犁师范学院 数学与统计分院,新疆 伊宁 835000)
1 引言及主要结果
近年来,许多学者研究了依赖于解的梯度项的拟线性椭圆问题
(1)
(2)
正解的存在性。其中1 由于我们寻求的是问题(2)正解的存在性,为研究问题的方便,我们作如下假设: (A1)对于所有的t<0和ζ∈N,有f(t,|ζ|p-2ζ)=0成立。 (A2)对于所有ζ∈N,有成立。 (A3)存在q∈(p,p*),使得对于所有ζ∈N,有成立,其中 (A4)[4]假定函数f满足Ambrosetti-Rabinowitz超线性条件,即存在θ>p,使得对于所有t>0和ζ∈N,有 成立。 (A5)存在m,n>0,使得对于所有s>0和ζ∈N,有F(s,|ζ|p-2ζ)≥msθ-n成立。 (A6)对于任意的ζ∈N,函数关于t>0是单调递增函数。 (A7)存在常数ρ1,ρ2>0,对于任意的ζ∈N,t1,t2∈[0,ρ1]及|ζ|ρ2,有 |f(t1,|ζ|p-2ζ)-f(t2,|ζ|p-2ζ)|M1|t1-t2|p-1 成立。 (A8)存在常数ρ1,ρ2>0,对于任意的ζ∈N,t∈[0,ρ1]和|ζ1|,|ζ2|ρ2,有 |f(t,|ζ1|p-2ζ1)-f(t,|ζ2|p-2ζ2)|M2|ζ1-ζ2|p-1 成立。 下列不等式在证明结论过程中起着重要作用 (3) 其中,Dp是一个实数,〈·,·〉是N中的内积。 (4) 显然问题(4)具有变分结构,因此问题(4)弱解的存在性问题可转化为它的能量泛函的极值问题。定义问题(4)的能量泛函为 首先,我们证明能量泛函Jτ满足山路定理的几何条件。 引理2.1[5]假定Ω是具有C1边界的N(N≥3)中的有界开区域且0∈Ω。设- 证明:由条件(A2),(A3)和(A4)知,存在δ>0及D>0成立 |F(t,|ζ|p-2ζ)| 根据引理2.1,我们做以下估计: 证明:由条件(A5)和引理2.1知 (5) 由于θ>p,从而当s足够大时(5)式右端小于等于零。引理2.3证毕。□ 下面我们证明问题(4)正解的存在性。 证明:由引理2.2和2.3知,泛函Jτ(u)满足山路定理的几何条件。由没有(PS)条件的山路定理(参见文献[4])可知,存在一个序列{un}⊂W1,p(N),使得Jτ(un)→dτ和成立, 其中 dτ=infγ∈Γmaxt∈[0,1]Jτ(γ(t))>0 而 Γ={γ∈C([0,1],W1,p(N)):γ(0)=0,γ(1)=Iv0}, 且v0和I的定义与引理2.3中的一致。 由条件(A4)知 因此,存在一个正常数D4成立 D4‖un‖pdτ+‖un‖。 由于{un}在W1,p(N)中有界,从而存在一个子序列(仍然用{un}表示)和uτ∈W1,p(N),使得当ptp*时,{un}在W1,p(N)中弱收敛于uτ,{un}在N)中强收敛于uτ及un(x)在N中几乎处处收敛于uτ(x)。由文献[6]知,在N中几乎处处收敛于此外,在文献[7]中,对于所有的ψ∈W1,p(N),当n→时成立 再根据勒贝格控制收敛定理(参见文献[8]),对于所有的ψ∈W1,p(N),当n→时成立 因此,对于所有的ψ∈W1,p(N),有成立。 若uτ≡0,我们证明存在一个序列{yn}⊂N和σ,R>0,使得 (6) 定义vn(x)=un(x+yn),我们利用N中的平移不变性可以得到,Jτ(vn)→dτ和并且,vn在W1,p(N)中弱收敛于vτ,vn在Lp(BR(0))中强收敛于vτ,其中vτ是能量泛函Jτ的一个临界点。由(6)知,vτ是非空的。引理2.4证毕。□ 证明:由于uτ不恒等于0,由条件(A2)和(A3)知 故 (1-D5δ)‖uτ‖pD6D‖uτ‖q。 引理2.5证毕。□ 证明:由条件(A6)知 取函数v0(同引理2.3),由条件(A5)知 dτ 故 ‖uτ‖ 引理2.6证毕。□ -div(|x|-ap|un|p-2un)+V(x)|un|p-2un=f(un,|un-1|p-2un-1) (Pn) 利用(Pn+1)和(Pn),可得 因此 ‖un+1-un‖pun|p-2un)-f(un,|un|p-2un)](un+1-un)dx 利用条件(A7)和(A8)可以做以下估计: 利用Hölder不等式得 ‖un+1-un‖ 由于系数h小于1,且序列{un}在W1,p(N)中强收敛于u,从而,{un}在W1,p(N)中是一个柯西序列,并且对于所有的n∈N+,有‖un‖≥R1成立,故在N中u>0。定理1.1证毕。□

2 不依赖于解的梯度项问题











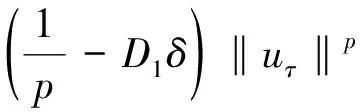



3 定理1.1的证明