基于PSO-SVM的手势识别方法研究

2019-09-02胡命嘉宫玉琳王锋

长春理工大学学报（自然科学版） 2019年4期

胡命嘉，宫玉琳，王锋

（长春理工大学电子信息工程学院，长春 130022）

手势动作识别即是通过传感器采集手势动作所产生的相关信息，来识别手势动作的一种方法，sEMG蕴含着丰富的肌肉动作信息，能反映肌肉的运动状态，通过分析不同类型动作的sEMG差异，即可区分出不同的动作模式［1］，且信号的强弱取决于肌肉的活动量大小［2］，因而sEMG在人机交互、康复医学以及体育科学等领域具有较高的实用价值。

随着对sEMG的不断深入研究，国内外现已取得了一定的成果。文献［3］从前臂的4块肌肉上采集4路sEMG，再提取5个特征，通过BP神经网络对sEMG进行分类识别，取得了较高的识别准确率；文献［4］通过将信号的5种特征参数相融合，利用LDA分类器进行分类识别，验证了在不同特征组合和维数下，都能取得较好的成果；文献［5］设计一套基于肌电控制的辅助型机器人外骨骼，通过基于贝叶斯决策的线性判别分析方法判别运动类别，对于5类动作的平均在线识别率达到了95%以上。但科研人员不仅要考虑识别的准确率问题，还要考虑实时性、差异性等问题，要进行更深入的研究。

本文通过MYO臂环采集上肢动作时产生的肌电信号，通过经PSO优化的SVM分类器对4种手势动作进行识别，取得了较好的分类效果。

1 手势识别方法

经MYO臂环采集的信号数据，由蓝牙传至电脑后，对数据进行处理与识别，手势识别方法如图1所示，主要包括起始点检测、特征提取和模式识别三个部分。

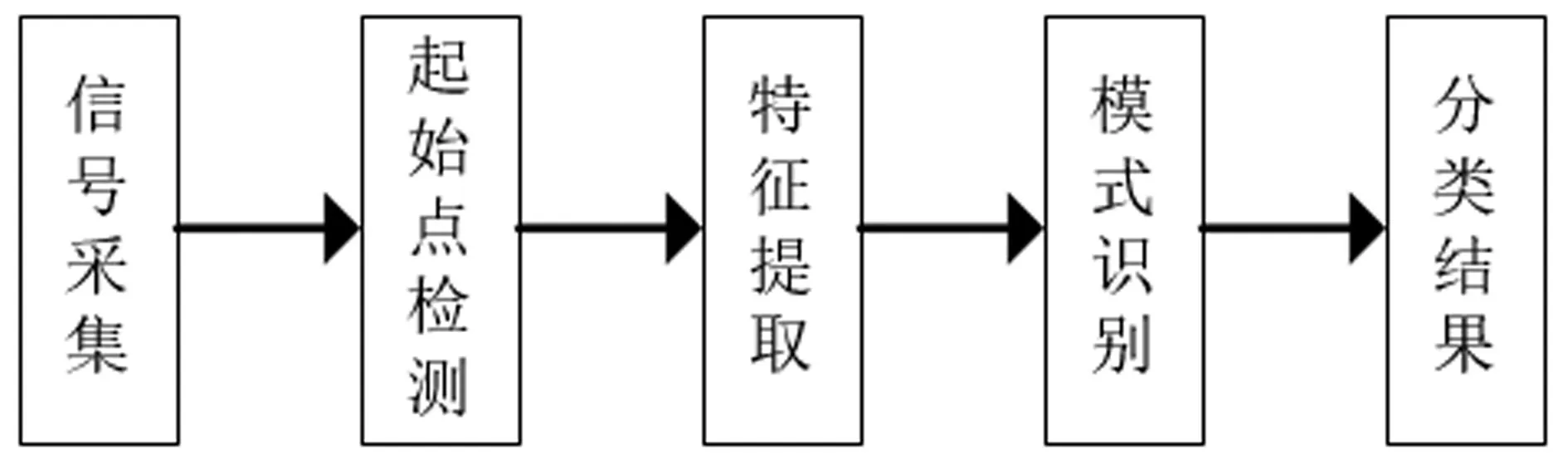
图1 手势识别方法

1.1 信号采集

为获得表面肌电信号，需要将人体产生的生物电信号转换为电路中的电压信号，在实际运用中，常通过肌电信号釆集设备获取人体肌电信号［6］。目前国内外研制了各种各样的肌电信号采集设备用于采集表面肌电信号，例如Delsys公司研制的Trigno16通道肌电信号无线釆集系统，能够接收40米内的肌电信号传感器信号；美国的ATHOS公司研制了一套肌电信号采集衣，将肌电信号传感器内嵌在训练衣上用于采集和分析人体运动时的肌电信号；加拿大Thalmic Labs公司所研发的MYO臂环，由弹簧扣将8个传感器等距离的排列在一起，可以佩戴在手臂上的任意位置，用来检测肢体动作时所产生的肌电信号，再用蓝牙将采集到的信号数据传输到计算机中。

考虑到实验操作的可行性和便捷性，本文通过MYO臂环采集手掌外张、手掌内张、握拳、张手四种手势动作所产生的表面肌电信号作为试验数据，进行研究。四种手势动作如图2所示，图2（a）为放松状态，图2（b）-图2（e）为四种手势动作，在数据采集过程中，规定放松-动作-放松为一次完整的动作，每种动作完整重复48次。

图2 四种手势动作示意图

1.2 动作起始点检测

动作起止点的检测方法有阈值法、标准差检测法、移动平均法等，本文选择将阈值法与移动平均法相结合作为判断动作起始点的方法，步骤如下：

（1）先对每种动作的8个通道的原始sEMG数据进行绝对值处理再滑动求和，记为sum_emgI，滑动长度L=50：

式中，N为采样点的长度，I为通道个数，xk为采样点。

（2）再求单个 sum_emgI的平均值，记为emg_MAVI(L)：

（3）再将I个通道的emg_MAVI()I信号相加，根据设定的阈值寻找动作起止点，找出有效的数据段：

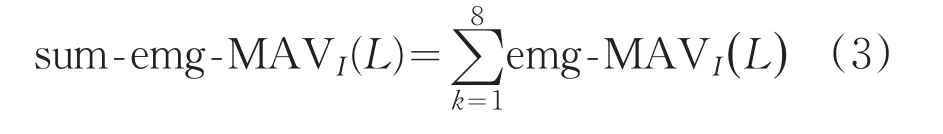
1.3 特征提取

特征选择是动作模式识别的关键。sEMG携带有不同手势动作的信息［7］，特征提取的目的是将不同手势动作尽可能区分，通过sEMG的某一特征数据来表示。目前在肌电信号分类方面主要的特征提取方法有时域特征、频域特征、时频特征。因时域特征也能获得较好的分类特性，且具有计算量少、获取迅速等优点，本文选取时域特征作为分类标准，为平均绝对值（MAV）、过零点数（ZC）、波形长度（WL）。

平均绝对值如（4）式所示：

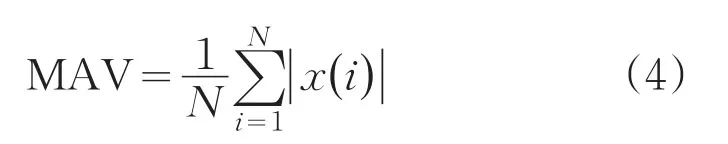
过零点数如（5）式所示：

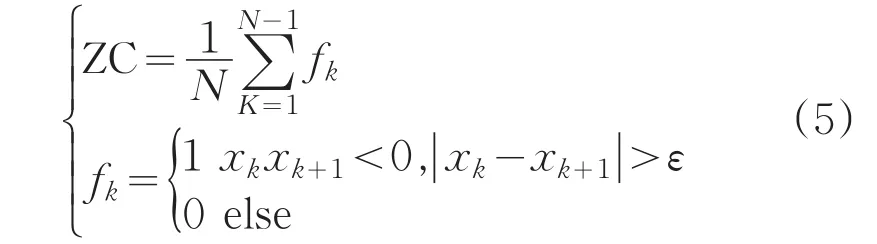
波形长度如（6）式所示：

在实验过程中，提取一次动作的24维特征样本数据（即MYO臂环的每个通道提取3个时域特征）。

1.4 SVM分类器

模式分类是指通过分类器对输入的特征向量进行归类的过程，分类器是一种数学模型，根据一定的数学算法，对输入的特征向量进行辨识，并将这些特征向量所属的类型输出。本文选择的分类器为支持向量机（SVM）。SVM是1995年由Vapnik提出的一种监督式机器学习方法，用于解决小样本、非线性、高维特征的分类问题，其基本原理为：将二分类问题中的非线性特征映射到高维空间，使得非线性特征在高维空间线性可分，再在高维空间构建超平面实现对样本的分类［8］。图3（a）为SVM原理示意图，现有两种不同类的样本，存在多条直线可以将两类坐标分开，但是否存在最优方案？SVM分类器即定义如下规则：若一条分割的直线离坐标点太近，则会受到噪声的影响，则不是最佳的。因此，目标是找到一条分割线，要求离所有的样本点都尽可能的远，即最优超平面，如图3（b）所示。

图3 SVM说明

现假设超平面为f(x)，其表达式如式（7）所示：

δi定义为特征向量xi到超平面的几何距离，如式（8）所示：

式中，m为训练样本数量。

引入拉格朗日乘子后，优化函数转变为：

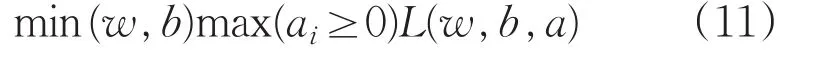
此优化函数满足KKT（Karush Kuhn Tucher）条件，则通过拉格朗日对偶将优化问题转化为等价的对偶问题来求解。根据KKT条件中的对偶互补，有：

若ai＞0，则有yi(w*x+b)=1，即点在支持向量上，否则如果ai=0，则有yi(w*x+b)≥1，即样本已经被准确分类或在支持向量上。

虽然SVM分类器具有适应性和泛化能力强，有效解决非线性、样本量少等优点，但是分类效果会受到数据模式的限制，且受惩罚参数C、核半径参数g的影响较大。

2 PSO-SVM分类器设计

考虑到SVM分类器受惩罚参数C、核半径参数g的影响较大，且人为难以找出合适的参数，现引入粒子群优化算法（PSO）对SVM分类器进行优化，寻找合适的参数。

2.1 粒子群优化算法

PSO算法最早是由Kennedy等人于1995年提出的，源于对人工生命和鸟群捕食行为的研究，其基本核心是利用群体中的个体对信息的共享从而使得整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得问题的最优解。

算法中粒子速度与位置通过迭代进行更新，迭代公式为：

2.2 PSO-SVM分类器

PSO对SVM的优化是为了得到一组误差最小的惩罚函数与核函数，使得优化后的分类器能够取得更好的分类效果，其基本思想如下：

（1）初始化粒子群。设所求问题的自变量有M维，种群大小为N，则初始化粒子的位置信息表示如下：

式中，ω为惯性权重保持原来速度的系数，本文中设定为0.6；k为当前迭代次数；c1，c2是学习因子，分别是粒子跟踪自身历史最优解的权重系数和粒子跟踪群体最优解的权重系数，分别取值为1.6与1.9；μ和ρ是均匀分布于［0，1］区间的随机数。

反复执行（2）与（4），直到达到最大进化代数，或达到所要求的收敛精度。

算法整体过程如图4所示。

图4 PSO优化SVM参数的算法流程图

3 实验结果分析

3.1 起始点检测实验结果

为寻找合适的动作起始点，如（3）式所示，将各个通道信号的平均绝对值（MAV）相加，选取0为判断动作起始点的阈值，0以上的信号为实验所需部分。图5为8个通道原始数据的波形图，图6为将取各通道的平均绝对值后的波形图，其中有用部分的数据段分别为89-192，462-625，937-1102，1409-1549，1892-1999。

图5 八个通道原始数据波形图

图6 八个通道MAV叠加波形图

3.2 动作分类实验结果

将处理后的信号数据代入到分类器中，对比SVM分类器和PSO-SVM分类器。在SVM分类器在训练数据数量为5时，其准确率只有74%，如图7所示，而PSO-SVM分类器在测试集数据数量为5时，其分类的准确可达到94%，如图8所示。定义类别标签1为手掌外张，标签2为手掌外张，标签3为握拳，标签4为张手。粒子群优化算法的迭代过程如图9所示，随着迭代次数的增加准确率逐渐趋近于最佳参数的适应度。

图7 测试集数据为5的SVM分类结果

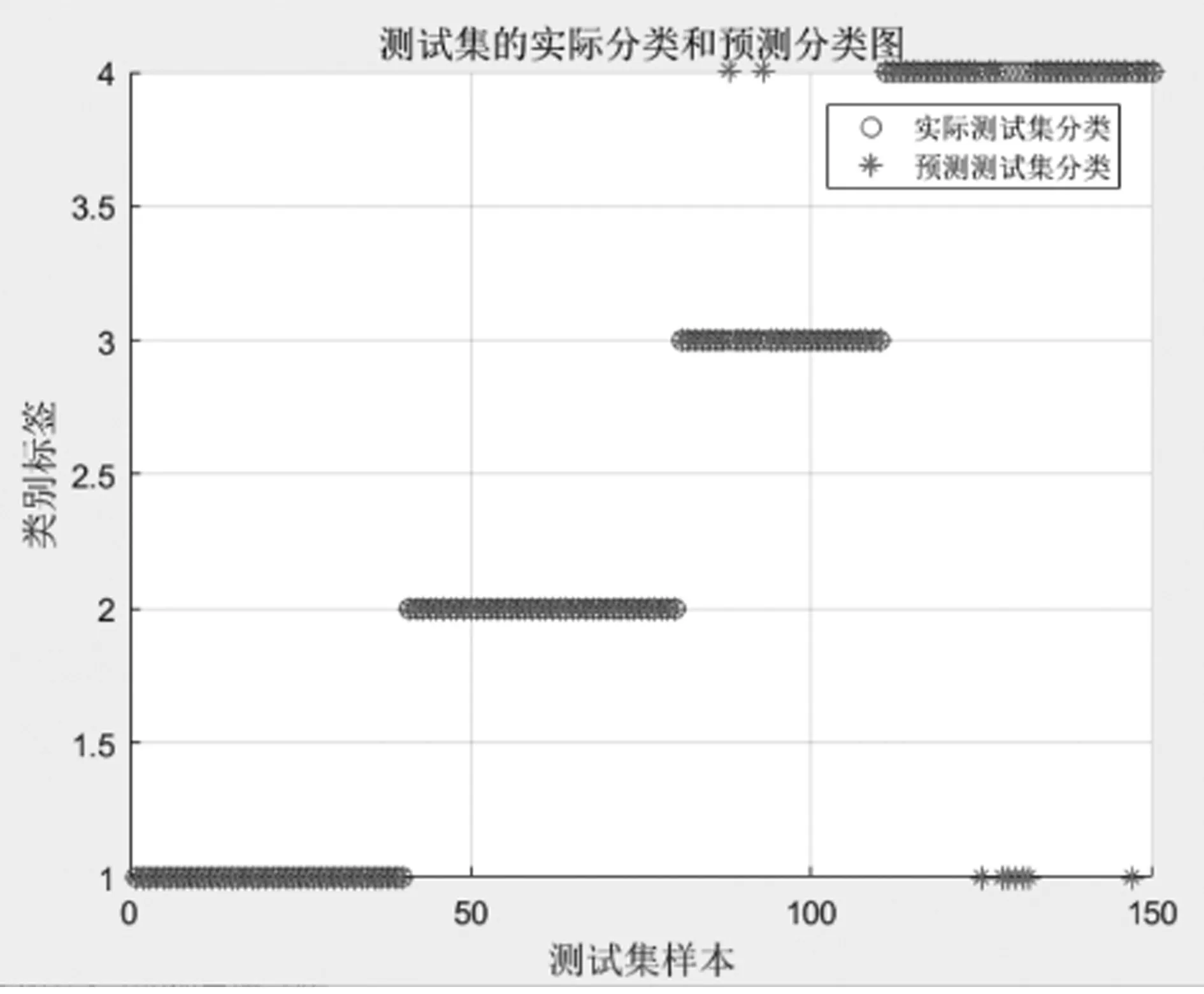
图8 测试集数据为5的PSO-SVM分类结果

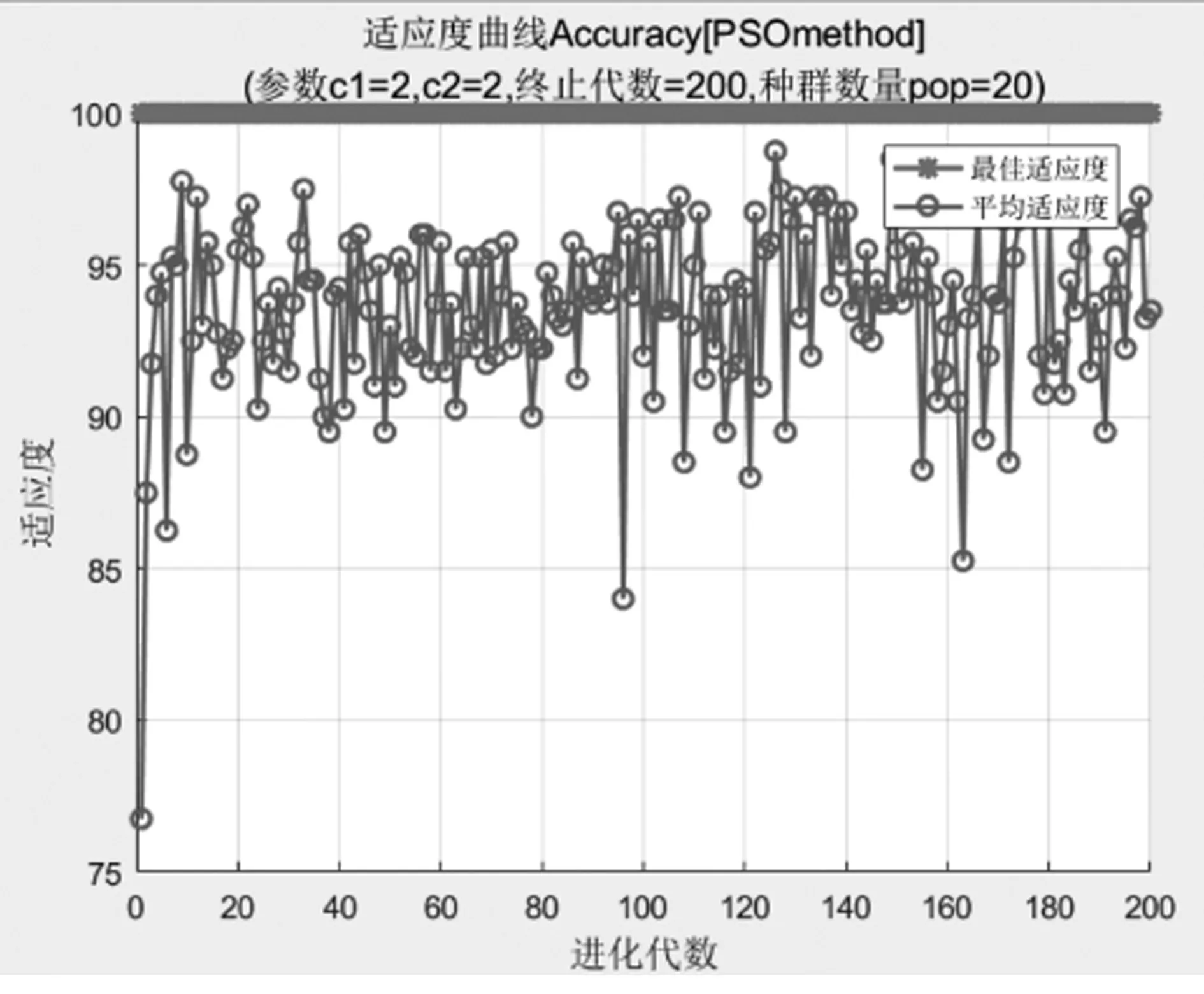
图9 PSO寻找最佳参数准确率曲线图

当训练数据数量都为8时，经实验结果证明：SVM分类器的分类准确率为79.3%，PSO-SVM分类准确率为97.6%，分别如图10、11所示，PSO的迭代过程如图12所示。

图10 测试集数据为8的SVM分类结果

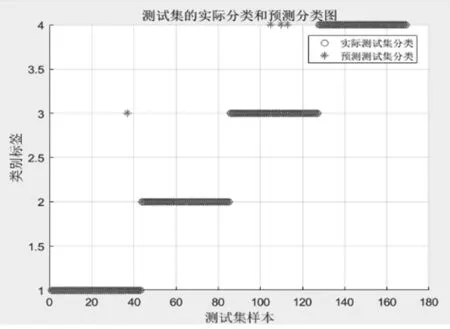
图11 测试集数据为8的PSO-SVM分类结果

图12 PSO寻找最佳参数准确率曲线图

再将测试集数据数量依次改为10、15，两者的分类效果如图13所示，其中横坐标处的5、8、10、15分别表示训练集的数据数量为5、8、10、15。

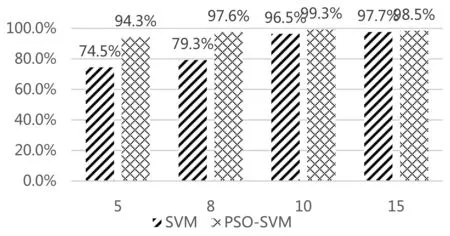
图13 SVM与PSO-SVM的准确率对比

由图13可知：SVM分类器的平均识别率为86.8%，而PSO-SVM的平均识别率为97.4%，当训练集的数据较少的情况下，PSO-SVM的分类效果较SVM分类效果明显提高很多；在分类器的训练数据较充充足的情况，由于分类器内部训练较成熟，两者差异较小，但PSO-SVM的分类效果依然比SVM要好，由此可见PSO对SVM分类器有了较好的优化。