基于蝙蝠算法的无线传感器网络定位研究

李鹏，陈桂芬，刘欢

（长春理工大学 电子信息工程学院，长春 130022）

无线传感器网络WSNs（Wireless Sensor Networks）是当前信息科学技术领域研究的热点之一，可实现特殊情况下信号的收集、处理和发送。由于其独特的学科交叉性，成为了二十一世纪极具发展潜力的关键技术。无线传感器网络是仅次于互联网的第二大网络，具有低成本、体积小、传输距离远等优势，广泛应用于军事、医疗环境监测等方面［1］。无线传感器网络是物联网最基本的组成部分，它对于实现各种类型数据融合和远程控制功能起到了不可替代的重要作用。定位是无线传感器网络重要的支撑技术。

DV-Hop算法是目前应用最广的一种无需测距的定位算法。但是已知节点与未知节点的距离计算存在误差，导致DV-Hop算法定位精度不高。多年来国内外学者针对传统DV-Hop提出了多种改进算法，文献［2］在DV-Hop算法中引入介质访问机制来调节距离误差；文献［3］将RSSI策略引入到DV-Hop算法节点距离计算中，减小节点间误差，提高定位精度；文献［4］提出单纯形法与遗传算法相结合的混合算法用于计算未知节点坐标，以提高定位精度；文献［5］提出了遗传粒子群优化的DV-Hop的定位算法，有效解决了局部搜索的定位精度问题；文献［6］提出了加权DV-Hop定位算法和Min-Max修正算法，达到提高定位精度的目的；文献［7］针对信标节点密度提出基于DV-Hop的修改算法，从源头上减小误差；文献［8］将模拟退火算法应用于基于测距修正的DV-Hop算法；文献［9］提出基于跳数修正和改进粒子群优化DV-Hop定位算法，进一步优化定位精度。近几年蝙蝠算法是一种群智能优化算法，在准确性和有效性方面相较其他算法有很大优势，且没有许多参数要调整，为DV-Hop算法误差校正提供了一种新的研究思路［10］。

综合考虑以上算法的优缺点，提出了一种将改进后的蝙蝠算法应用到DV-Hop算法的新算法，首先对频率公式中的参数β进行改进，在此基础上在蝙蝠算法中引入自学习算法，在提高节点距离计算精度的同时，避免算法陷入局部最优。仿真结果表明，与DV-Hop算法和BADV-Hop算法相比，SLBA-DV-Hop算法在不同实际情况下均能有效提高节点的定位精度。

1 DV-Hop算法及误差分析

1.1 DV-Hop算法

DV-Hop算法是根据矢量路由的原理提出的一种无需测距的定位算法，该定位算法的过程可以分为3步。

第一步：WSN中的参考节点首先利用洪泛算法将自身位置信息向全网广播，网络中的参考节点通过典型的距离矢量交换协议广播自身位置分组，使得网络中的所有节点获得距离参考节点最小的跳数信息。

第二步：.每个参考节点利用其它参考节点的位置信息和相隔最小跳数计算平均每跳距离，并将其作为一个校正值广播到网络中。网络中未知节点接收到该信息后，将其与到各锚节点的跳数的乘积作为未知节点到各锚节点距离的估算量。然后通过锚节点计算HopSize，并广播到整个网络。

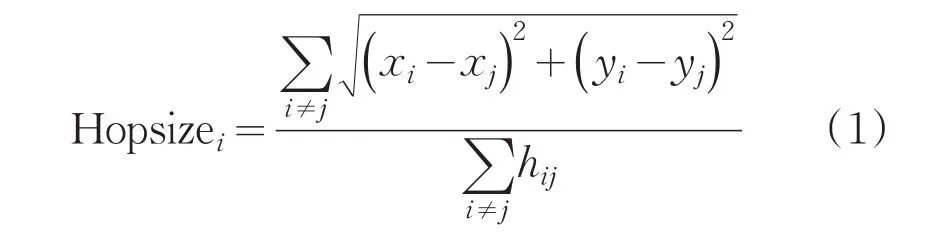
式中，Hopsizei表示参考节点i的平均跳距，坐标（xi,yi），（xj,yj）分别表示参考节点i与参考节点j的坐标。hij为节点i与节点j之间的最小跳数。再由下式计算参考节点与未知节点距离。

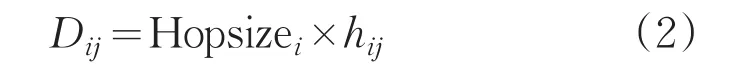
第三步：当知道未知节点与两个以上参考节点的距离时，使用三边测距法或极大似然估计法，计算未知节点坐标。

1.2 DV-Hop算法误差分析

（1）跳距误差：节点大部分是随机抛洒在想要监测的各个区域，很容易产生参考节点分布不均的情况。这种情况下，节点间的跳距会有较大差距，这种情况下只是利用平均跳距乘以最小跳数来计算就会带来很大误差。

（2）锚节点密度：综合考虑参考节点成本和能量消耗的情况下，参考节点数量不会很多，在需要大范围的监控区域只有十几个甚至几个参考节点时，其定位精度会受到很大影响，无法满足高定位精度的实际需求。

（3）算法本身的计算误差：三边测距法计算方法虽然简单精炼，但一旦未知节点与参考节点距离存在较大误差，就会随着每步的进行逐渐放大误差，极大似然估计法计算方法较复杂一些，对较大误差的估计距离无过滤作用。

2 SLBADV-Hop算法的节点定位

2.1 蝙蝠算法的步骤

蝙蝠算法是受自然界中的蝙蝠依靠回声定位方法避开障碍以及搜寻食物行为的启发，并将遗传进化机制与多智能体系相结合发展而来的一种新型群体智能启发式算法。当蝙蝠出发时，响度最大而脉冲发射率最小，蝙蝠探测到猎物之后，在飞向猎物的过程中，响度逐渐减小而脉冲发射率不断增大。蝙蝠正是通过这种回声定位方式进行精确定位以确定飞行方向和搜寻猎物的。将蝙蝠算法视为函数minf(x)求目标变量为X=(x1,x2,…,xd)T的优化问题，具体步骤如下：

第一步：蝙蝠种群初始化，蝙蝠在N维空间随机飞行看做即函数在某一区域的初始解。蝙蝠飞行产生的搜索声波频率范围为［fmin,fmax］、最大脉冲响度A0、最大脉冲发射率R0。脉冲响度衰减系数α，脉冲发射率增加系数γ，搜索精度ε或最大迭代次数iter_max。

第二步：随机初始化蝙蝠的位置xi，并根据适应度值的优劣情况寻找当前的最优解x∗，即初始种群的最优位置，然后调节此时的脉冲频率，更新蝙蝠个体i在t时刻的位置和速度，具体公式如下所示。

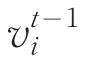
第三步：蝙蝠通过迭代缩小搜索范围后，会进入局部搜索阶段。蝙蝠会在它附近按公式（6）随机运动并产生一个新解xnew，而xold为当前时刻选出的最佳解。At表示t时刻蝙蝠响度平均值。θ是一个随机数，在0～1之间均匀分布。

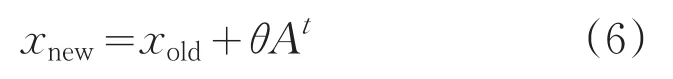
At表示t时刻蝙蝠响度平均值。θ为0～1之间服从均匀分布的随机数。

第四步：蝙蝠种群个体在不断更新。当蝙蝠个体在t时刻接近猎物时，声波响度逐渐降低，同时脉冲速率逐渐增高，直到蝙蝠个体i搜索到猎物时Ai=0，此时声波停止。更新公式如下：

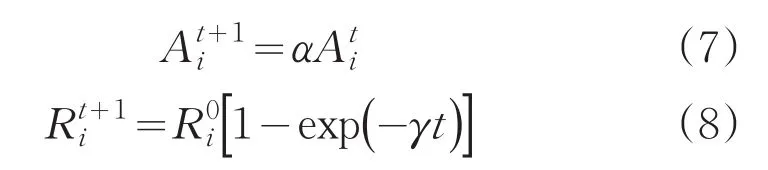
第五步：在所有蝙蝠的适应度值中找出当前最优解，重复第二、三、四步，找到最优解时或满足最大迭代次数后结束循环，最后通过最优解输出全局最优值。

2.2 蝙蝠算法适应值函数的设计

蝙蝠算法每次迭代结束后，蝙蝠所处位置的优劣都要通过适应值来判断。将蝙蝠种群中的每一个蝙蝠看做未知节点的一个随机解。适应值函数计算公式为：

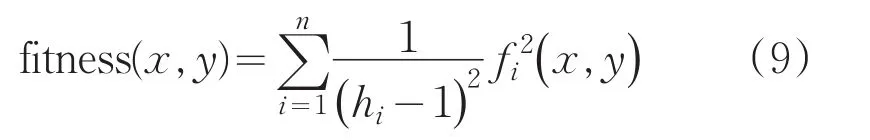
式中，n为参考节点的个数，hi为未知节点到参考节点的跳数。hi通过DV-Hop算法的第一阶段得到，而未知节点的估计距离是通过最小化适应度函数的目标值确定的。

2.3 蝙蝠算法的改进

2.3.1 改变参数β

蝙蝠在搜索定位过程中通过调整fi获得新的位置。在公式（3）中，β作为0～1之间均匀分布的随机因子，实质是蝙蝠个体的变异因子。该值越大，对fi的解作用越大，反之越小。因此合理改变β的值可以提高种群多样性，避免早熟。进而提高蝙蝠种群的寻优精度。

在基本的蝙蝠算法中，β是一个常数，并不随着蝙蝠搜索时间的变化而变化。现对β做如下定义：

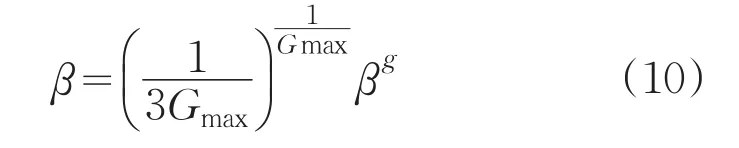
Gmax为最大迭代次数，g为蝙蝠当前迭代次数。迭代过程中，该算法通过改变β值，优化频率公式，改进后的频率更新公式如下：

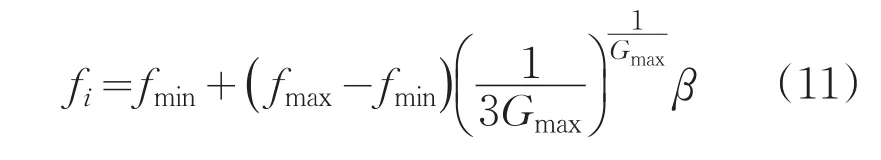
2.3.2 改进速度和位置更新公式

根据蝙蝠算法的原理和公式可知，蝙蝠算法的蝙蝠种群多样性很差，优化过程中极易陷入局部最优值。现对其加以改进，并将改进后的算法用于解决无线传感器网络定位问题，提高节点定位精度。假设蝙蝠个体拥有本身速度决定飞行方向和距离。他们可以自行判断t时刻本体的位置以及t时刻发现的最优位置。甚至可以发现该时刻其它蝙蝠个体发现的最优位置，蝙蝠综合这三点因素，“自行学习”最佳的飞行位置。

在标准蝙蝠算法中，蝙蝠速度只是当前位置的函数，提出的自学习算法中蝙蝠个体的飞行速度会随着蝙蝠位置的变化而变化。通过此自学习策略，蝙蝠个体通过迭代，逐步寻找当前最优蝙蝠的位置。假设蝙蝠i在n维空间的速度和位置分别为vi=(vi,1vi,2vi,d）以及xi=(xi,1,xi,2,xi,d），每进行一次搜索，蝙蝠通过跟踪两个最优解改变自己位置。第一个是蝙蝠个体本身找到的最佳解，记为a。第二个是整个种群该时刻找到的最优解，记为b。蝙蝠个体会根据这两个最优值更新自己的速度和方位，具体公式如下：

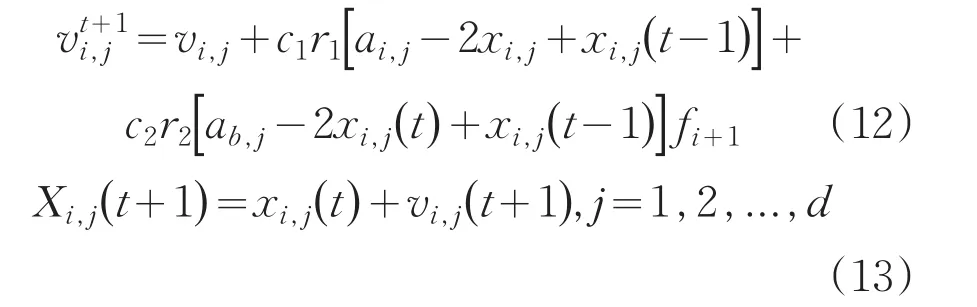
c1，c2为蝙蝠算法的自学习参数，是蝙蝠个体自学习和学习种群最佳个体的关键，这样才能保证个体对整体最优位置的搜寻。为保证算法整体性能，这里取c1=c2=2。

r1，r2是0～1之间均匀分布的随机数。

2.4 SLBADV-Hop算法定位步骤

（1）首先在待检测区域随机抛洒节点，进行经典DV-Hop算法前两步骤，获得所有节点与参考节点间的最小跳数信息以及每个节点与参考节点间距离。第三步应用改进后的自学习蝙蝠算法实现。

（2）设置如下参数：蝙蝠数量n，蝙蝠个体i，搜素空间d维，声波频率fi，脉冲发射率R(i)，响度A(i)。初始化蝙蝠种群中每个个体的速度和位置。采用自学习算法修改原蝙蝠算法中蝙蝠个体i在t时刻的位置。a，b分别为蝙蝠本身及种群找到的最优解，c1，c2为自学习参数。由公式（3）、（11）、（12）对蝙蝠个体的速度和位置进行优化更新。

（3）每次搜索完成后，如果蝙蝠i的位置好于上次迭代最佳蝙蝠的位置，则用公式（7）、（8）更新脉冲发射率和响度。

（4）找出当前具有最优蝙蝠个体的适应值函数以及当前速度和具体位置。

（5）重复步骤（2），（3），直到达到预先设定好的迭代次数。搜索结束后，处于最佳位置的蝙蝠就是未定位节点的最优位置近似值。

3 算法仿真

为了准确了解定位精度问题，用Matlab软件对改进后的算法进行仿真。假设理想条件下，在边长100m的正方形网络中，随机分布100个传感器节点，节点通信半径为40m。分别讨论不同参考节点数量，总节点数量以及探测区域面积对传统DV-Hop算法、BADV-Hop算法、SLBADV-Hop算法定位精度的影响。每种实验进行一百次，为减小定位误差，取一百次的平均值。节点定位误差用如下公式表示。

式中（xk,yk）是节点k的估计坐标，（x，y）为未知节点k定位后的坐标，节点k通信半径为R。

（1）参考节点比例对平均定位精度影响

边长为100m的正方形区域中，通信半径固定为40m。随机分布100个节点。参考节点比例分别为5%、10%、15%、20%、25%、30%。改变参考节点比例观测平均定位精度的变化情况。同时对三种算法进行仿真，仿真结果如下图。

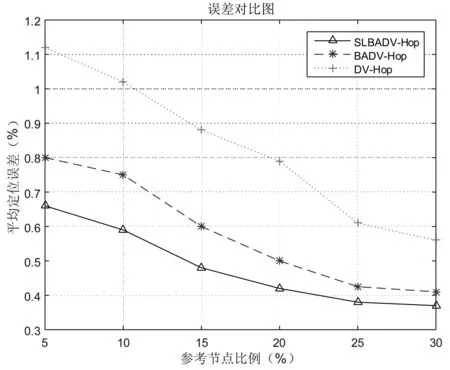
图1 节点总数不变参考节点比例改变的定位误差比较

从图中可以看出随着参考节点比例的提高，三种算法平均定位误差都在下降，但SLBADV-Hop算法定位误差明显小于前两个算法。当参考节点比例增大到15%以上时，定位精度误差有大幅度提高。但是当参考节点比例增加到一定程度时，三种算法的误差差距逐渐减小。

（2）网络节点总数对平均定位精度的影响

在边长为100m的正方形区域中，分别随机分布100、150、200、250、300个节点，通信半径固定为40m。参考节点比例15%。改变网络节点总数观测平均定位精度变化情况。同时对三种算法进行仿真，仿真结果如下图。

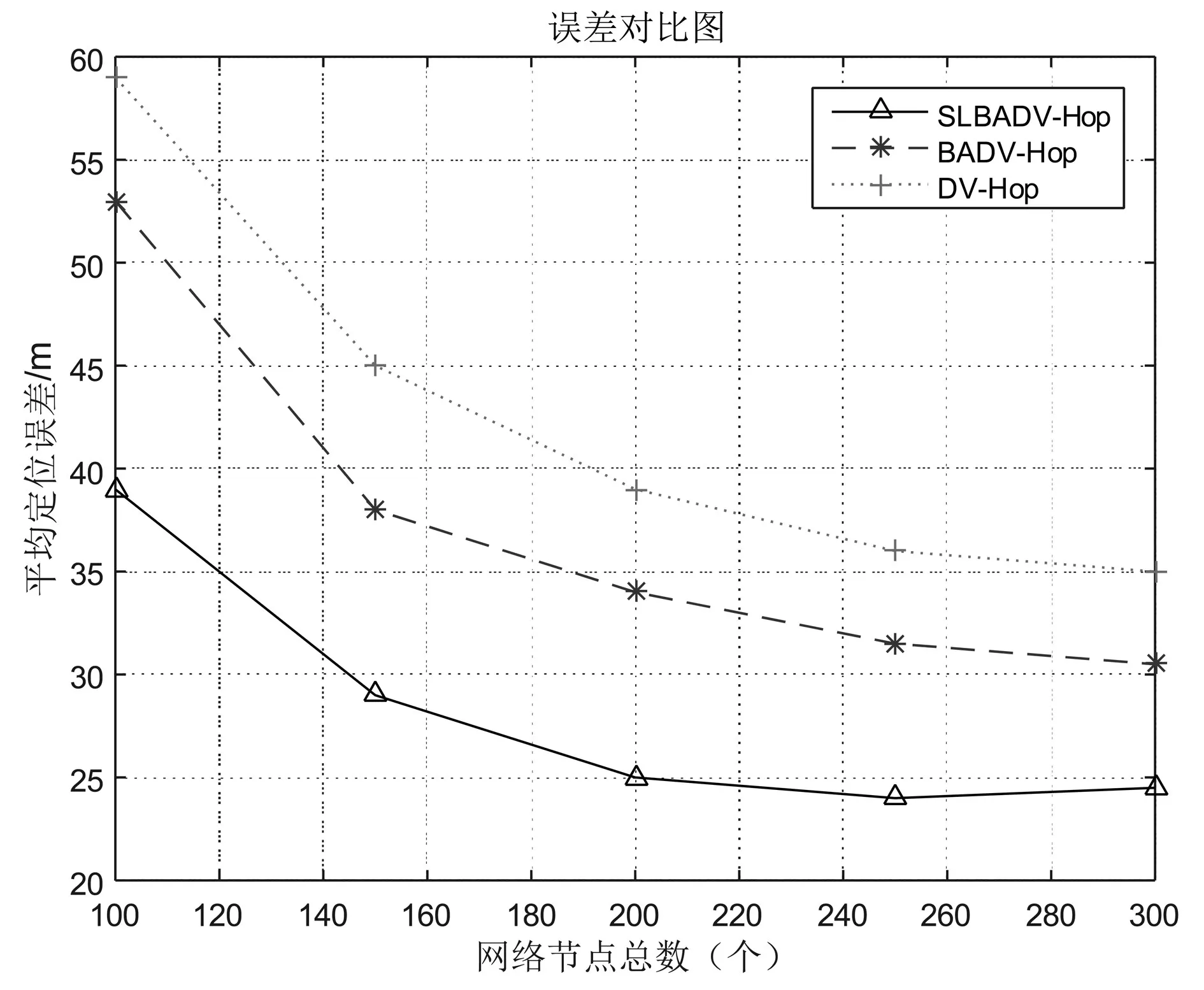
图2 参考节点比例不变节点总数改变的定位误差比较

从图中可以看出随着参考节点比例的提高，三种算法平均定位误差都在下降，其中SLBADV-Hop误差率是最低的。当总节点数介于100和150之间时误差下降最为明显，定位精度提高了20%左右。但是可以明显看出，当节点总数增大到一定数目时节点密度并没有大幅度提升，节点密度过大，节点间通信浪费了更多能耗，还增加了不必要的成本。所以应根据实际情况合理选择节点数量。

（3）定位区域面积对平均定位精度的影响

在边长依次为100、150、200、250、300m的正方形区域中，通信半径固定为40m，随机分布100个节点，参考节点比例15%。改变如上的定位区域面积观测定位精度变化情况。同时对三种情况进行仿真，仿真结果如下图。

图3 节点总数和参考节点总数不变定位区域面积改变的定位误差比较

从图中可以看出随着参考节点比例的提高，三种算法定位误差均有不同程度的提高，但SLBADV-Hop算法误差比前两者低很多。由于节点总数不变，定位区域增大，导致节点密度相对稀疏，降低定位精度。当边长超过260m时，误差增大的情况愈发明显。这种情况下，SLBADV-Hop算法依然保持了较低的误差。比应用于DV-Hop的蝙蝠算法平均提高了9.1%的定位精度。

4 结论

针对无线传感器网络定位误差较大的问题，提出了一种将DV-Hop算法与改进蝙蝠算法相结合的算法。改进了影响蝙蝠收敛性的参数β，又在蝙蝠速度和位置更新公式中引入学习因子，解决局部最优问题。仿真结果表明，本文提出的算法有效提高了节点的定位精度，且该算法迭代次数少，收敛性好，易于实现。由于本算法没有考虑障碍物密集度较高的情况，下一步工作中将随机设置一定数量的障碍物，使该算法应用范围更广。