基于相似分析和人工神经网络的管柱式气液旋流分离器压降预测模型

2019-09-02

中国海洋平台 2019年4期

(中国石油大学(北京) 过程流体过滤与分离技术北京市重点实验室，北京102249)

0 引言

深水油气是重要的能源资源。当前，国际海洋油气正迈向深水、超深水领域，管柱式气液旋流分离器(Gas Liquid Cylindrical Cyclone separator， GLCC)则是深水油气开发中的重要设备[1]。GLCC结构紧凑，既无内构件，也无运动件，且成本低[2]，对实现油气高效分离并保障管线输送安全起到至关重要的作用。GLCC结构如图1所示，其工作原理为：气、液两相流经与竖直筒体相切的倾斜入口管，经渐缩喷嘴加速后在竖直筒体上、下部分别形成气相、液相两股旋流。在离心力与重力的作用下，液相被甩到边壁，并形成向下的液相旋流，最后从下部液相出口排出，气相则边旋转边向上形成气相旋流，再从竖直筒体上部气相出口排出，由此实现气、液两相的分离。GLCC虽结构简易、作用原理简单，但分离器内部流体力学行为却极其复杂，其结构参数、操作参数、物料特性等因素均影响分离器的分离性能，截至目前，还未形成切实可行的性能预测方法，难以有效指导工业生产。

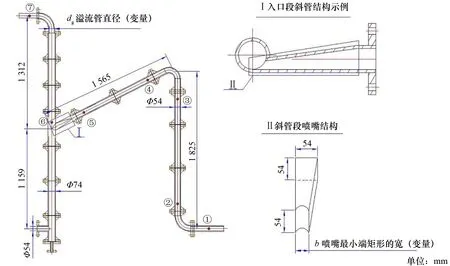
图1 GLCC结构与尺寸

相似理论用量纲分析或方程分析等方法导出相似准数，再依据相似原理建立试验模型(或试验台)，通过试验得出相似准数间的定量关系，以揭示物理现象的本质规律。运用相似理论进行模型试验经济性佳、针对性强且数据准确[3]。相似分析法已在各个研究领域得到了广泛应用：孙雪锋[4]基于几何相似原理对水力旋流器进行研究；罗晓兰等[5]以切流反转式水下油气分离器为对象，采用相似分析得到影响分离器性能的关键无因次参数，并对这些参数进行优化匹配，设计出满足工程要求的深海油气分离器。运用相似理论对GLCC进行研究具有一定的可行性。

人工神经网络是一种基于模仿生物大脑的结构和功能，采用数学和物理方法进行研究而构成的信息处理系统[6]。一般而言，先假定网络的结构已经确定，即已知计算单元的层数、每层的神经元数以及各层间神经元的关联，当输入与输出之间是非线性关系且训练数据库足够庞大时，人工神经网络可以出色地完成不同领域的问题[7]。褚良银等[8]以人工神经网络为手段，建立油-水分离旋流器的3层BP神经网络模型，该模型可根据物性参数、性能要求设计旋流器结构和操作参数；冯建成等[9]采用BP神经网络算法，建立的固-液水力旋流器模型，既可用于设备选型，又可用于优化旋流器参数。GLCC的性能指标与影响因素之间属于典型的多维非线性关系，采用传统的数学建模或理论分析方法很难对其精确描述，且一些理论函数关系往往是基于一定的假设基础获得的，相比而言，通过人工神经网络方法的非线性映射能力获得的预测模型更接近实际[10]。

然而，一直以来，影响神经网络的泛化能力，或者说外推能力的因素，除其自身内在算法外，一部分取决于被训练参数的影响，一部分取决于目标值与影响参数之间是否有很强的对应关系。一方面，被训练参数的水平值越多，隐含在参数之间的规律越能被挖掘出来；另一方面，若目标值与影响参数之间的关系较为简单，则通过一定的训练也能得到满意的结果。但是，往往由于某些客观原因，在目标值与影响值之间的关系较为复杂且被训练参数的水平值较少时，人们想获取未训练参数所对应的响应值，采用传统训练单因素法的人工神经网络所获得的结果是不理想的，它有其内在局限性。根据相似理论的特点，无量纲数可将多个因素进行关联，将其运用到神经网络学习中时：一方面，减少影响参数的个数，使原本被训练的参数变得不再独立，加强了影响参数之间的内在联系；另一方面，倘若通过该种方式获得的结果误差在合理的范围内(即便用传统训练单因素的方法也获得了理想的结果)，那么该结果更具有理论意义。因此，本文试图采用将相似理论与人工神经网络相结合的方式，以期建立对GLCC分离压降性能的预测。

1 BP神经网络基本原理及GLCC相似模化

1.1 BP神经网络

图2 BP神经网络结构图

BP神经网络，即基于误差反向传播(Error Back Propagation， EBP)的学习算法，是一种具有无反馈的、层内无互联多层结构的神经网络，由斯坦福大学的RUMELHART于1985年提出。BP神经网络由输入层、隐含层、输出层组成，信号经输入层逐层传递至输出层，属于前馈网络模型[11]。BP神经网络的学习过程包括正向传播和逆向传播两种。在正向传播的过程中，输入信号逐层传递至输出层：若输出值等于期望值，或二者差值在可接受的误差范围内，则学习过程结束；若输出层得不到期望值，则误差(二者之差)将按连接通路反向传播，并调整隐含层各节点的权值，使误差减小[12]。其结构如图2所示。

1.2 相似模化

影响压降的因素很多，本研究的液气体积比小于5%，故本文关注气相溢流压降。对于GLCC而言：影响压降Δp的几何参数有入口管直径d和长度L，管壁粗糙度ε，主筒体直径D和高度H，渐缩喷嘴小端的面积a×b，以及溢流管直径dg(见图1)；操作参数有气液相入口表观速度vsg、vsl，重力加速度g；物性参数有气液相密度ρg、ρl，气、液相动力黏度μg、μl，以及气液相界面张力σ。16个参数的量纲如表1所示。

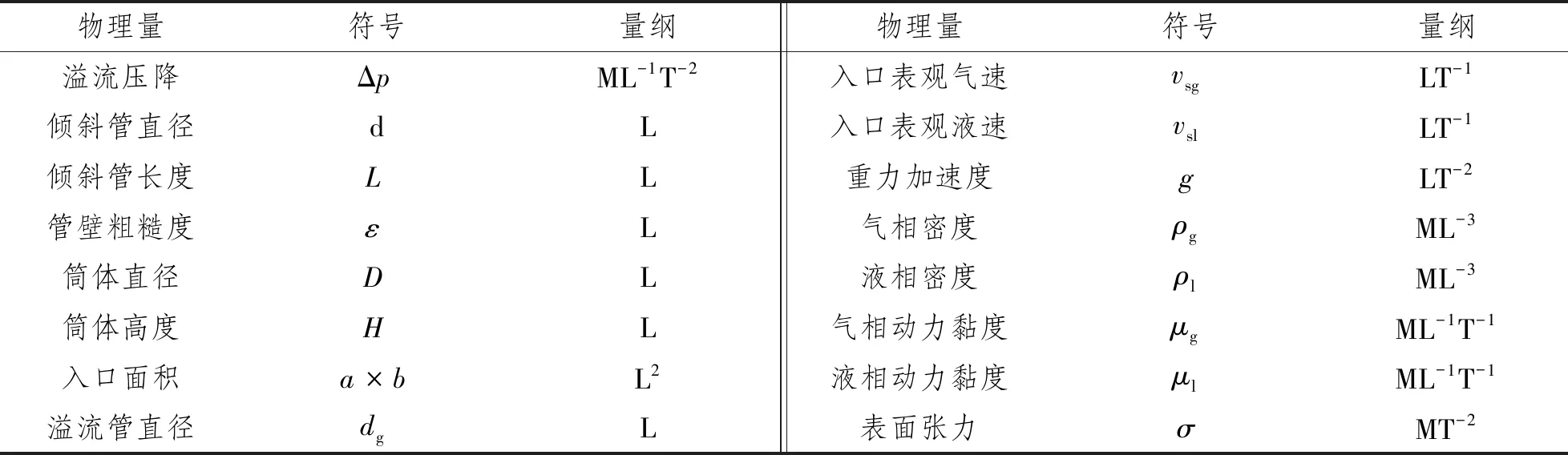
表1 各物理量量纲

本文所使用的GLCC模型的材料、高度、直径，以及倾斜入管的长度均未改变，在此前提下，依据伯金汉π定理，选取d、vsg和μg为基本物理量，将余下的物理量分别与3个基本物理量组合可获得表2的无量纲数群。

表2 无量纲数群

表2一共有10个无量纲数，再对其进行合理的幂乘组合，可得到7个相似准则数，如表3所示。

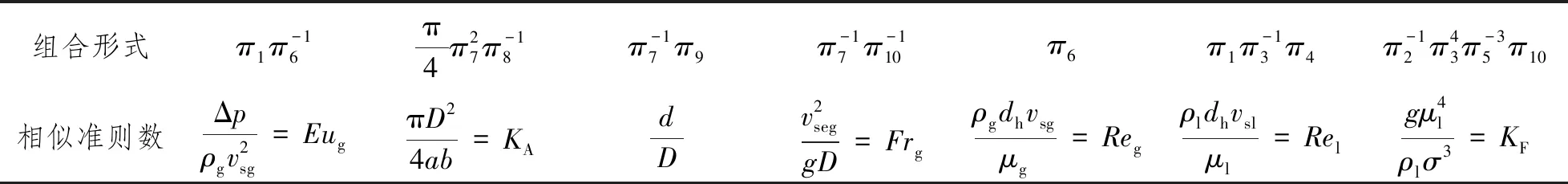
表3 相似准则数

表3中：KA为形状因数；KF为液膜表面波动数[13]。对于气相欧拉数Eug，本文考虑气液两相综合动能的影响，对其进行修正，表达式为

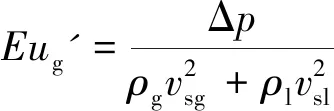
(1)

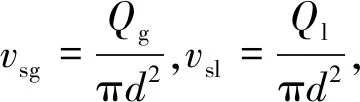
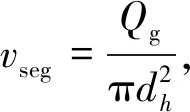
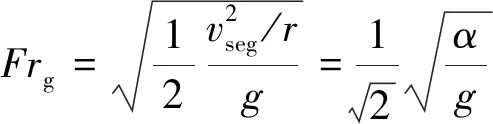
(2)

式中：r为GLCC竖直筒体旋转半径，m；α为离心加速度，m/s2。

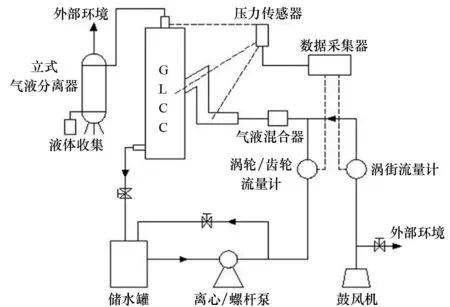
图3 GLCC试验装置示例

2 试验流程及参数范围

2.1 试验流程

试验装置及流程如图3所示。空气由型号为GHBH 7D536 2R7的高压风机鼓出，经型号为LUGB-80的涡街流量计测得体积流量Qg；液相由泵增压后经涡轮流量计测得体积流量Ql。气液两相经混合器充分混合后，一起进入GLCC进行分离：分离后的气相从GLCC上部气相排气口排出，再经立式丝网气液分离器后，最终排入环境中；分离后的液相从GLCC下部液相排液口返回至水箱以循环利用。在试验过程中，利用调节阀将平衡液位控制在竖直筒体轴向高度约900 mm[14]处，并利用RS 485数据采集系统对气液两相流量及压差信号进行实时在线采集(图1中①～⑦点为压力采集点)，通过在储水罐中放置通自来水的冷却盘管，将试验温度控制在25 ℃。需要指出的是，根据液相介质的不同，所使用的泵和流量计有所不同：对于水溶液，采用型号为40-200A的离心泵和型号为LD-25的涡轮流量计；对于油溶液，采用型号为G30-1的单螺杆泵和型号为LWGC-25的涡轮流量计。

2.2 影响参数范围

GLCC的结构参数、物性参数和气液处理量的改变均会导致Δp的改变。在本试验中：GLCC竖直筒体直径D=74 mm，倾斜管直径d=54 mm；3个矩形渐缩喷嘴最小端面积a×b分别为0.054 m×0.040 m、0.054 m×0.029 m、0.054 m×0.017 m，分别称作1#、2#、3#喷嘴；溢流管直径分别为30 mm、40 mm、54 mm，分别记作dg30、dg40、dg54；气相为空气(25 ℃时，其密度ρg=1.185 kg/m3，动力黏度μg=0.183 μPa·s)，液相为水、甘油(不同质量分数)，液相物性如表4所示；气相流量为80～220 m3/h，液相流量为0.3～3.3 m3/h。

表4 液相物性一览表

其中，液体密度ρl用50 mL密度瓶以及JA5003电子天平测得，动力黏度μl由NDJ-8S旋转黏度计测得，表面张力σ用Theta光学接触角测量仪测得，测量原理为悬滴法。被测液体温度由CH1006N恒温水箱控制。

3 人工神经网络的建模与分析

3.1 BP神经网络建模

在搭建的试验平台上，共获得数据650组。为了体现神经网络的预测能力，将影响参数划定范围，其中用于神经网络训练的数据范围如表5所示，共计217组。相应地，用于神经网络训练和预测的无量纲数的范围即被划定。

表5 作为训练数据的参数范围

基于MATLAB的BP神经网络共3层：输入层、隐含层和输出层。输入参数为：形状因数KA、相似单纯数dg/D、气相弗劳德数Frg、气相雷诺数Reg、液相雷诺数Rel和液膜表面波动数KF(在训练中发现，将液膜表面波动数取对数lgKF后预测模型的准确度更高，这可能是由数据归一化后3个KF之间的量级相差过大导致的，因此此处取lgKF)共6维。输出参数为：溢流阻力系数ζ(ζ=2Eug')共1维。隐含层节点数的选择关乎预测模型的精度[15]：节点数若选择过少，BP神经网络将不能建立复杂的映射关系，容错性差；节点数若选择过多，BP神经网络学习时间增多，且精度不一定很高。然而，截至目前，关于节点数的选择，尚无完整的理论指导，常采用以下经验公式确定：

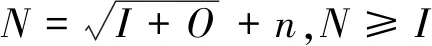
(3)

式中：N为隐含层节点个数；I为输入层节点数；O为输出层节点数；n为0～10之间的整数。对于本文而言，I=6，O=1，即N的取值范围为3～13，经过多次试验后确定隐含层节点数N=7。至此，建立了结构为6-7-1的3层BP神经网络模型。

为使BP神经网络收敛效果明显，利用mapminmax函数对数据进行归一化处理，使数据分布于[-1,1]之间。根据BP神经网络的原理，需使目标值与期望值之间的差值最小，这是一个快速并准确寻找最小值的优化问题。在解决多维最优化问题的方法中，常采用的算法有梯度(最速下降)法、牛顿法、Levenberg Marquardt (LM)[16]算法等。其中，LM算法是改进版的牛顿法，本质上属于最小二乘算法，该算法通过增加矩阵对角元个数使函数陷入局部极小值的机会大幅度减小，是处理多维非线性优化问题使用最广泛的一类算法。本文学习算法选用LM算法。隐含层与输出层传递函数的选择同样至关重要，选择不同的函数对预测结果会产生很大的影响。事实上，传递函数的选择在很大程度上依赖于所训练的样本，目前对于传递函数的选定仍没有准确的理论指导，多取决于人们的经验和数次的尝试。本文隐含层采用logsig激活函数，输出层采用purelin激活函数，训练的收敛误差平方和设置为0.001，训练的最大次数设置为1 000，网络的学习率设置为0.05。图4的结果依次是训练样本、验证样本、测试样本和全部样本的回归系数R值，其值越接近1，表明训练结果越好。

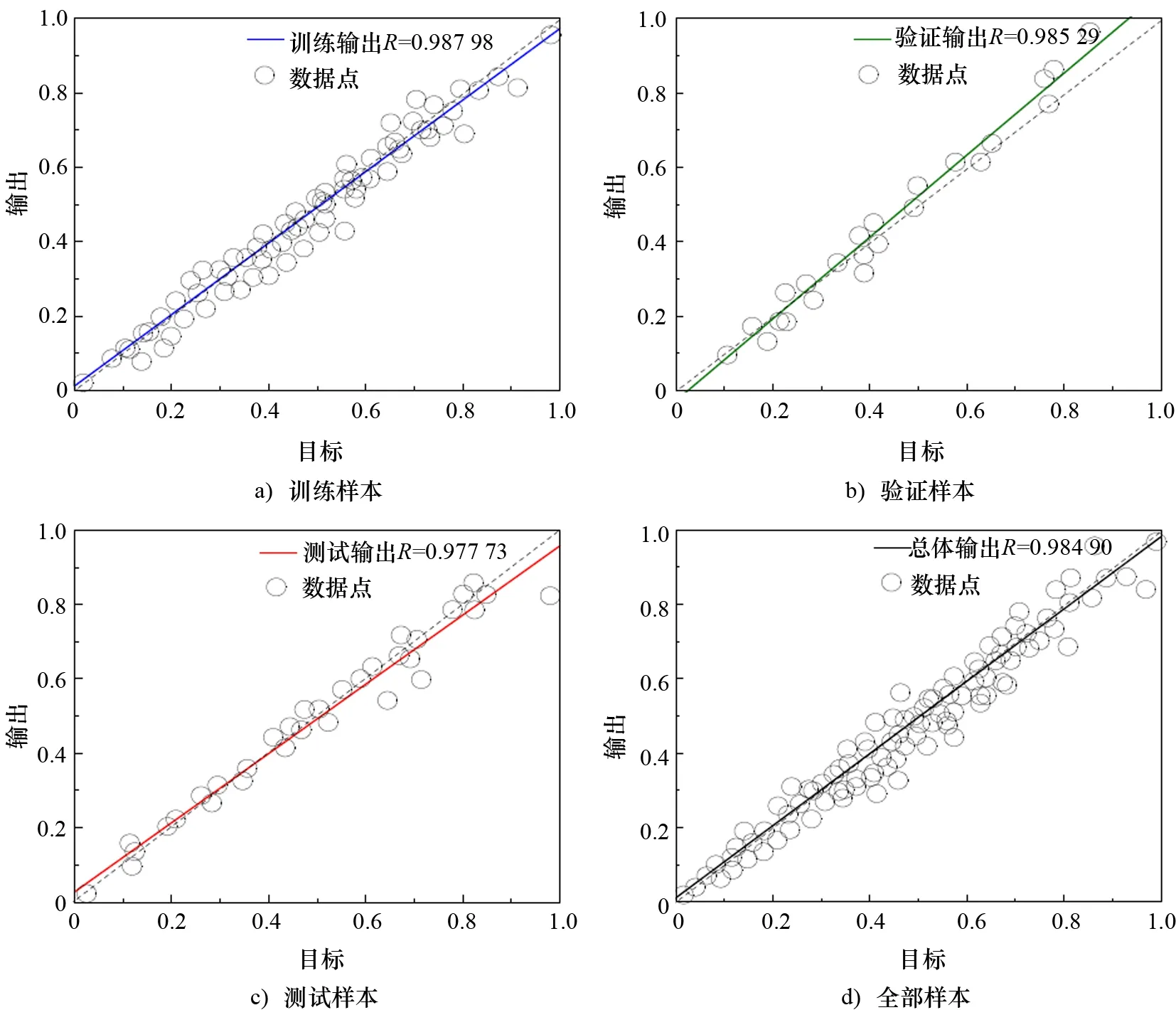
图4 网络训练结果

3.2 预测值与试验值对比

本文从结构参数、操作参数和液相物性等3个角度分别预测其对GLCC溢流阻力系数的影响。图5a)预测2#和3#喷嘴对溢流压降的影响。可以看出：对于已经参与训练的2#喷嘴而言，预测值与试验值几乎吻合，相对误差(Relative Error，RE)小于5%；对于3#喷嘴而言，在小气量下，预测值略高于试验值，在大气量下，预测值略低于试验值，但整体趋势一致，图中最大相对误差(Maximum Relative Error，RE.Max)为10.52%。此外，在其他条件一致的前提下，3#喷嘴的溢流压降大于2#喷嘴，这是因为：喷嘴截面积的减小导致进入GLCC筒体的气液相旋流切向流速增大，静压能可转化的动压能增大[17]；流体进入筒体后剧烈撞击筒体壁面，造成局部湍动程度增强，相应地，在气液分离过程中，气液旋流损失也增强，可造成压力损失。图5b)预测了溢流管直径dg=30 mm和dg=54 mm对溢流压降的影响。可以看出，溢流管直径对溢流压降的影响有很好的规律性：对于已经参与训练的dg30而言，模型依然可较准确地实现预测；对于dg54而言，在小气量下，预测值略低于试验值，当气量超过140 m3/h后，预测值略高于试验值，但整体趋势一致，图中RE.Max为9.31%。在相同的操作条件下，随着溢流管直径的减小，ζ值明显增大，说明在一定范围内溢流压降随溢流管直径的减小而增大。这是因为：筒体与溢流管连接处的过流面积突然减小产生的涡旋引起能量损失；此外，速度场突变引起旋流强度变化，并造成附加摩阻损失也致使GLCC溢流压降发生变化。图5对于2#喷嘴和dg30的预测结果也说明：利用神经网络将无量纲数作为影响参数进行训练，对已经参与训练的样本(或训练范围之内的样本)而言，几乎可以实现结果的重现，这与传统地将单因素作为影响参数进行训练以预测训练范围之内的样本的效果是一致的。

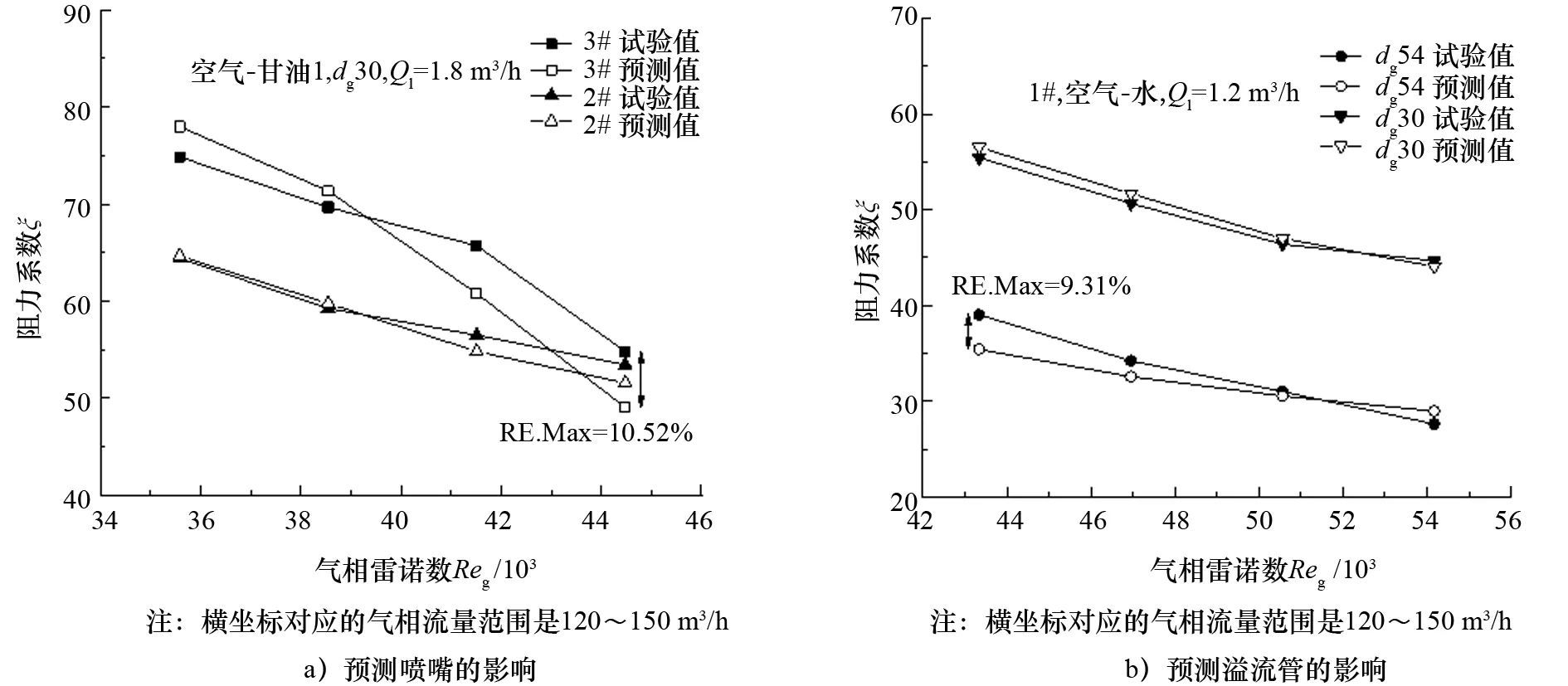
图5 预测结构参数对GLCC溢流压降的影响

图6所示的是预测操作参数对GLCC溢流压降的影响，可以看出：阻力系数ζ随Reg和Rel的变化均显示出很好的规律性。如图6a)所示：当液量一定时，阻力系数ζ随Reg的增大而减小；当液量增大时，阻力系数ζ也相应增大。当Ql=2.7 m3/h时，预测值小于试验值；当Ql=3.0 m3/h时则相反。图6b)表明阻力系数ζ随Rel的增大而增大，当气量增大时，阻力系数ζ也相应增大，整体上预测值偏小。事实上，气液量的增大使流体速度增加，导致流体内部各层间的速度差变大，流体运动需要克服更多的流动阻力，故使得压降增大。从图6也可以发现RE.Max随着气液量的增大而变大，这意味着预测模型可能是在一定的范围内保证精度。

图6 预测操作参数对GLCC溢流压降的影响

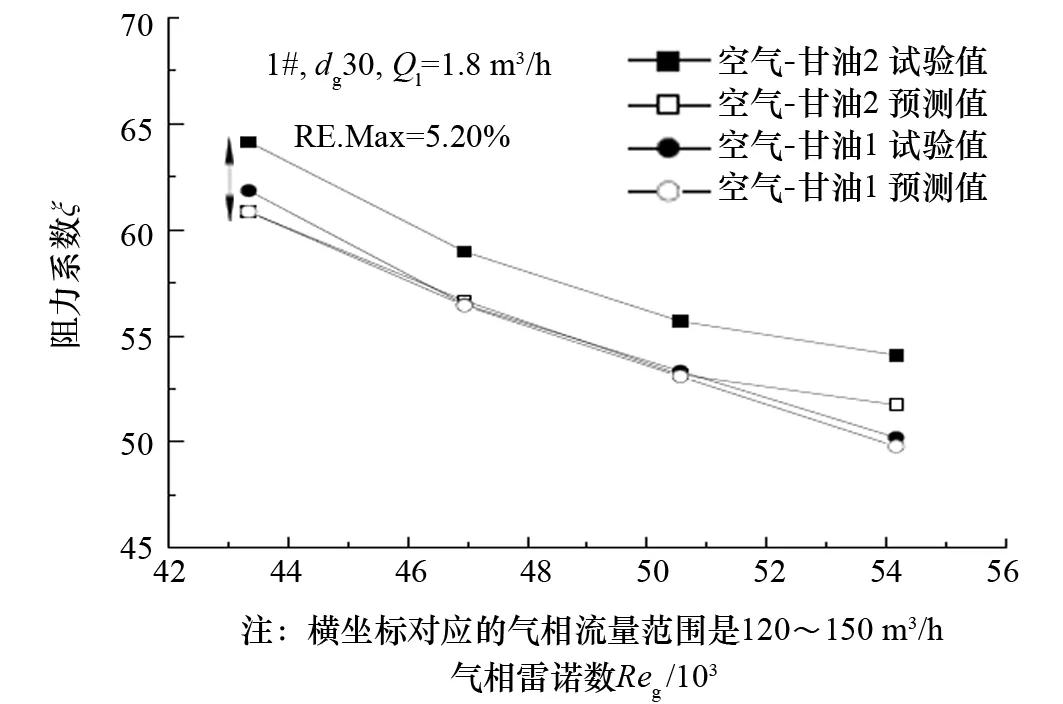
图7 预测液相物性对GLCC溢流压降的影响

一直以来，人们还未完全理解流体物性对溢流压降的影响机制，这是由于流体物性包含密度、黏度、表面张力等参数，这些参数之间的交互作用以及各相之间参数的交互影响错综复杂，从理论上综合考虑这些参数对影响性能的作用机制不是一件易事。本文尝试利用液膜表面波动数KF表征液体物性对GLCC溢流压降的影响，KF综合了惯性力、黏性力、表面张力以及重力的影响。如图7所示：当预测空气和39%甘油溶液时，平均相对误差小于3%；当预测空气和47%甘油溶液时，预测值与试验值趋势一致，且最大相对误差为5.20%。另外，由图7可知：在相同的条件下，液相介质为47%的甘油溶液比液相介质为39%的甘油溶液阻力系数更大，这是因为流体黏性的增加致使气液间拖曳力增大；气液界面的波动情况也不容忽视，表面张力越小，液膜表面波更易发展，造成溢流压降增大。

在样本数据范围一致的前提下，本文也利用BP神经网络模型对传统的单因素对GLCC溢流阻力系数的影响进行训练和预测，结果表明，在训练结果理想的前提下，预测效果并不令人满意，很难同时实现不同参数对性能值较为准确的响应(相对误差小于15%)。这也说明在不考虑其他影响的前提下，将相似理论与人工神经网络结合是一种有利无弊的思想与方法。