海洋平台圆管构件抗撞性能数值分析
2019-09-02秦晓宇1袁奎霖
秦晓宇1, 袁奎霖, 钱 缘
(1.中船第九设计研究院工程有限公司, 上海200063; 2.大连理工大学 船舶工程学院 工业装备结构分析国家重点实验室, 辽宁 大连 116024)
0 引 言
随着深海油气勘探开发需求扩大,海洋平台得到了广泛的应用。然而,平台在进行钻井和采油作业时,守护船因操作不当而撞击平台立柱结构的事故时有发生。通常,圆管构件抵抗冲击的能力有限,在撞击导致局部结构损伤严重时极有可能造成平台整体坍塌,危及人员生命和财产安全。因此,开展海洋平台碰撞性能研究,揭示圆管结构在碰撞过程中的损伤变形机理,成为平台结构抗撞设计的重要课题。
早期学者对于圆管构件在受撞击场景下的动力响应研究大多基于圆管变形机理假设,总结碰撞力或能量耗散的经验公式。THOMAS等[1]较早地根据刚性撞头冲压圆管试验,总结出两端简支圆管在横向载荷作用下的3种变形模式;WIERZBICKI等[2]提出了横向载荷、轴向载荷及弯矩联合作用下的变形理论,指出圆管的局部凹陷与边界条件密切相关;KHEDMATI等[3]研究发现轴向预紧力的大小直接影响圆杆抵御横向载荷的能力。上述研究都基于准静态载荷的假设条件,但碰撞问题是强非线性瞬态冲击问题,早期的准静态模型已经不能满足更为准确的动力响应分析要求。
随着有限元方法的发展,数值模拟成为国内外学者研究碰撞问题的重要手段。VILLAVICENCIO等[4]利用弹塑性模型模拟方形压头侧向撞击夹持梁,并研究夹持宽度对动力响应的影响;甘进等[5]运用ANSYS/LS-DYNA软件模拟船中部位侧向撞击导管架平台的场景,认为将杆件的边界条件简化为两端刚性固定是合理的;包杰[6]使用ABAQUS软件分析三角楔形头侧向撞击典型T、K管点的动力响应,所得结果与试验数据吻合度较高;TRAVANCA等[7]基于LS-DYNA软件分析平台与船舶碰撞的能量耗散问题;杨亮[8]和金梦菊[9]分别利用流固耦合方法对导管架平台遭受带有球鼻艏的商船正向碰撞问题进行分析,并得到最大碰撞力的估算公式。不过,在以上研究中被撞杆件的几何尺寸均较为单一。
为模拟海洋平台桩腿遭受船头撞击的场景,本文对碰撞系统进行简化,以刚性楔形撞头撞击圆管构件场景为研究对象,运用LS-DYNA软件分析撞击过程中碰撞力、能量和塑性变形等动态响应特征,并与试验结果对比,验证了数值模拟方法的有效性。在此基础上,研究圆管无因次化几何尺寸参数的改变对碰撞损伤变形的影响,研究结果对海洋平台圆管构件的防撞性能设计具有指导意义。
1 碰撞试验数值模拟与验证
本文采用动态显式弹塑性有限元方法,对单根圆管试件受楔形头自由下落撞击试验[10]进行数值仿真。试验分别测量3种不同冲击高度(1.0 m、2.0 m和3.6 m)条件下测点处的碰撞力-时间曲线和塑性变形。
为了模拟试验过程, 根据真实试件的几何尺寸和质量[10],利用MSC.Patran软件建立有限元模型。 如图1所示,圆管长L为1 600 mm,直径d为102 mm,壁厚t为16 mm,圆管两端连接在150 mm×150 mm 的正方形端板上,将端板上的8个螺栓孔处设置为刚性固定边界条件。
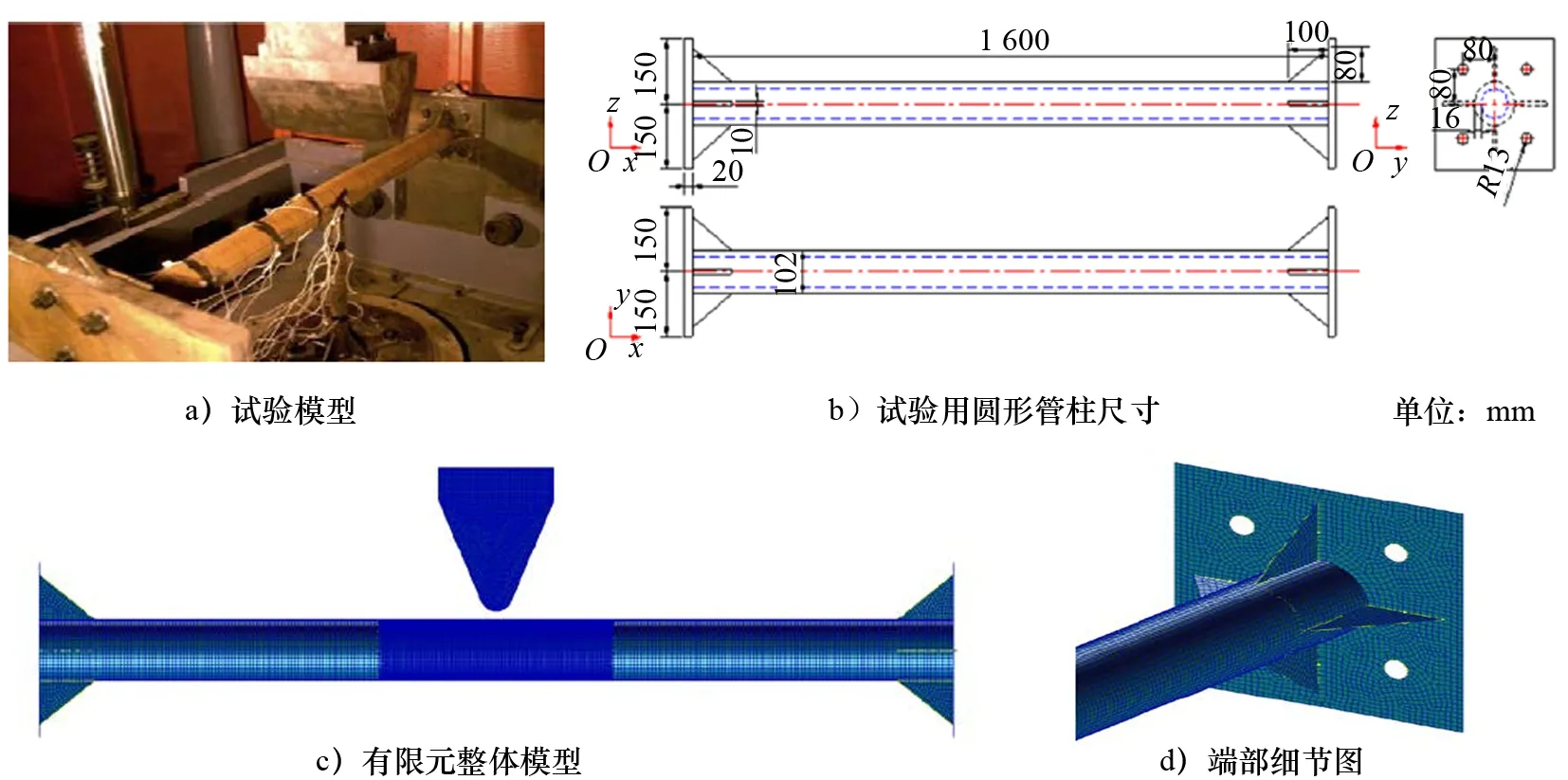
图1 楔形头撞击圆管试验与数值仿真
圆管材料为Q235钢,根据真实应力-应变数据(见图2),采用MAT24_PIECEWISE_LINEAR_PLASTICITY弹塑性材料模型。 此外,为考虑冲击过程中的应变率效应,采用Cowper-Symonds强化模型,即
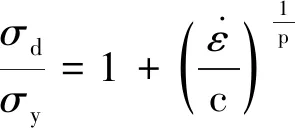
(1)
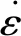
撞头设置为刚体,其质量与初始速度条件如表1所示。上述模型采用LS-DYNA软件进行计算,并与试验结果进行对比,验证模型的有效性,如图3所示。
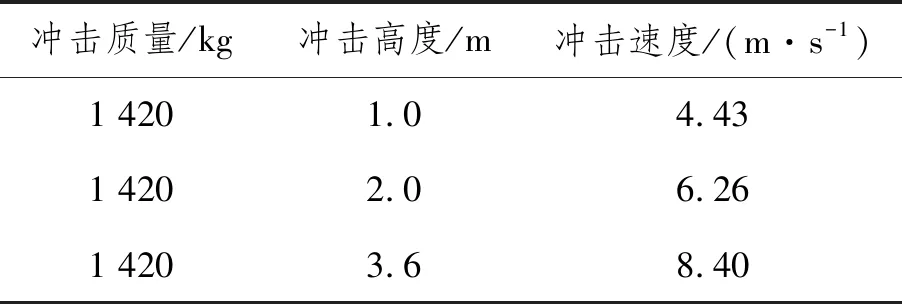
表1 模拟工况
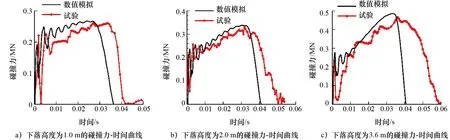
图3 不同冲击高度下碰撞力-时间曲线的数值模拟与试验对比
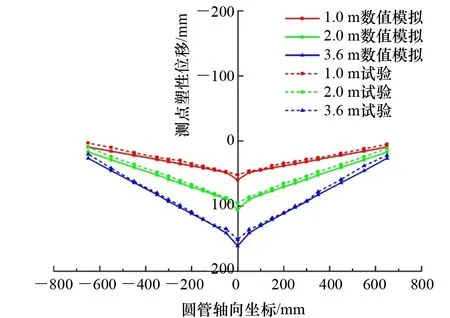
图4 测点变形测量与数值预测对比
由图3可知,在3种不同冲击高度工况下碰撞力-时间曲线的变化趋势基本一致,都经历了振荡、稳定加载和卸载等3个阶段。在振荡和稳定加载阶段,数值模拟与试验结果吻合较好,但二者的卸载时间存在一定差异。由于结构冲击损伤变形主要取决于加载阶段撞击力的最大幅值,因此认为卸载阶段的差异并不影响最终结果的有效性。
圆管上表面由于冲击产生的整体变形和局部凹陷(即撞深)是表征结构损伤程度的主要参数。试验通过激光测距仪测量21个测点处的位移变化,从而确定管件的整体变形,而数值模拟则提取卸载后对应测点处节点的位移差值。如图4所示,二者吻合较好。此外,由于试验中较难直接测得撞击点处附近的局部凹陷变形,通过与DNV[11]、AMDAHL[12]和WIERZBICKI 等[2]的碰撞力-撞深公式进行对比(见图5),验证了圆管结构撞击仿真技术的准确性和可靠性。
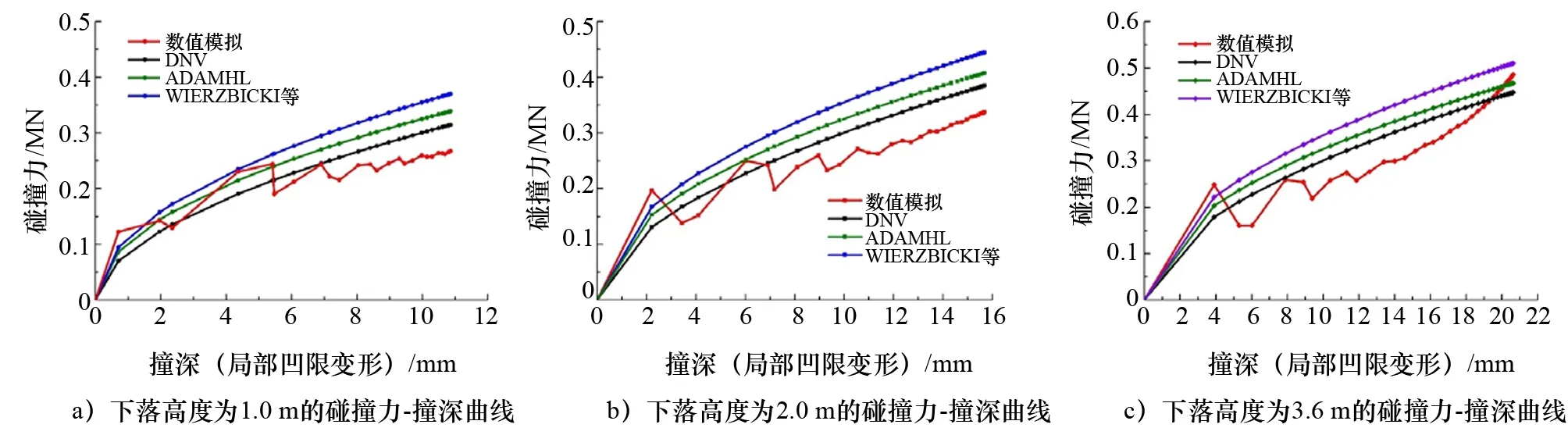
图5 不同冲击高度下碰撞力-撞深曲线的数值模拟与理论公式对比
2 几何尺寸参数对抗撞性能的影响
由于试验研究费事费力且受到许多条件的限制,采用不同几何尺寸的圆管结构进行大量试验存在困难,因此本文在上述模型基础上,通过数值模拟研究无因次尺寸参数L/d、d/t的变化对圆管结构抗撞性能的影响,包括碰撞力、圆柱杆件变形,以及结构遭受撞击载荷过程中的能量耗散情况。
2.1 L/d的影响
保持圆管直径d与壁厚t不变,建立3种不同长度L的圆管碰撞模型进行计算,得到相应的碰撞响应过程。具体尺寸如表2所示。

表2 壁厚不变下圆管构件尺寸汇总
(1) 碰撞力。无因次尺寸参数L/d反映了圆管结构的柔度。如图6所示,在相同的冲击速度条件下:L/d越小,则碰撞力越大,且碰撞力随撞深的变化速率也加剧;相反, 随着L/d增大,加载过程中结构的弹性振动变得更明显,碰撞力的波动也随之增大。
(2) 整体变形与局部凹陷。由于撞头撞击圆管跨中位置,整体变形关于中点是对称的。由图7可知,L/d越大,碰撞后圆管整体变形也越大。相反,由图8可知,撞击区域的局部凹陷变形随L/d增大而变小,与碰撞力呈相同趋势。
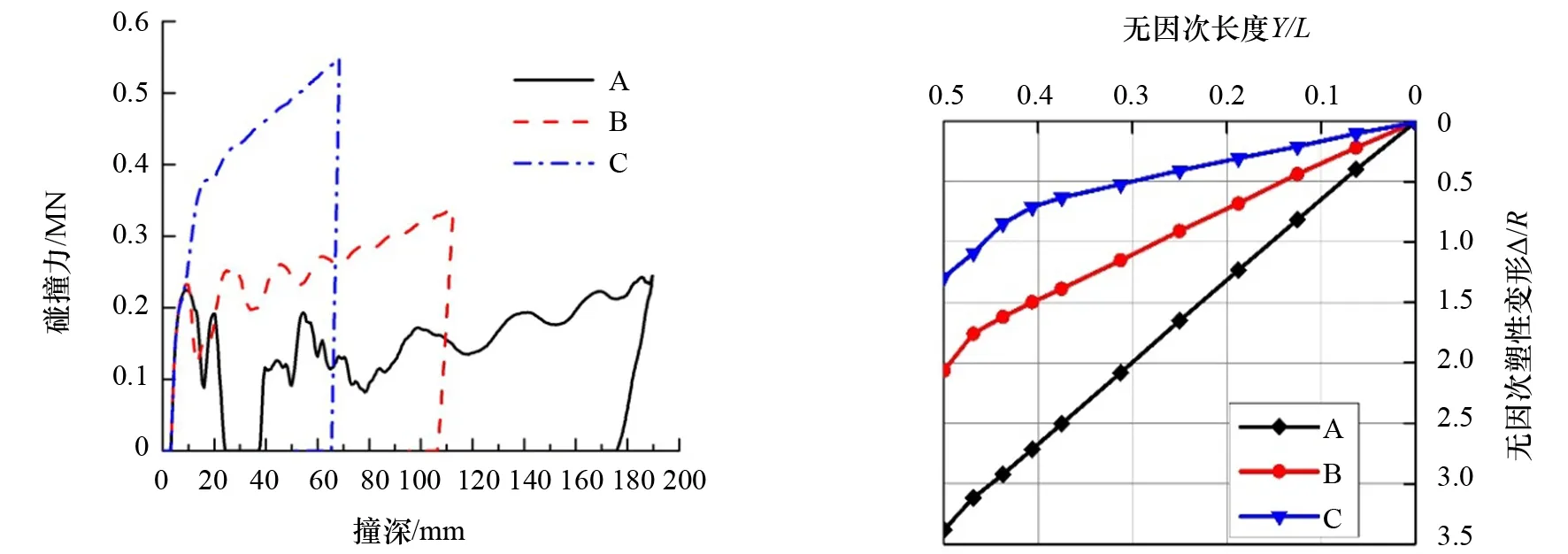
图6 不同L/d下的碰撞力-撞深曲线 图7 不同L/d下的整体变形
(3) 能量耗散。本文定义碰撞过程中圆管吸收的能量占总能量的比重为能量吸收率Ein。不同L/d条件下圆管构件的能量吸收率如图9所示。从图9可知,能量吸收率Ein随L/d增大而降低, 这是因为L/d即柔度较大时的圆管构件在撞击作用下产生的局部塑性凹陷变形较小。
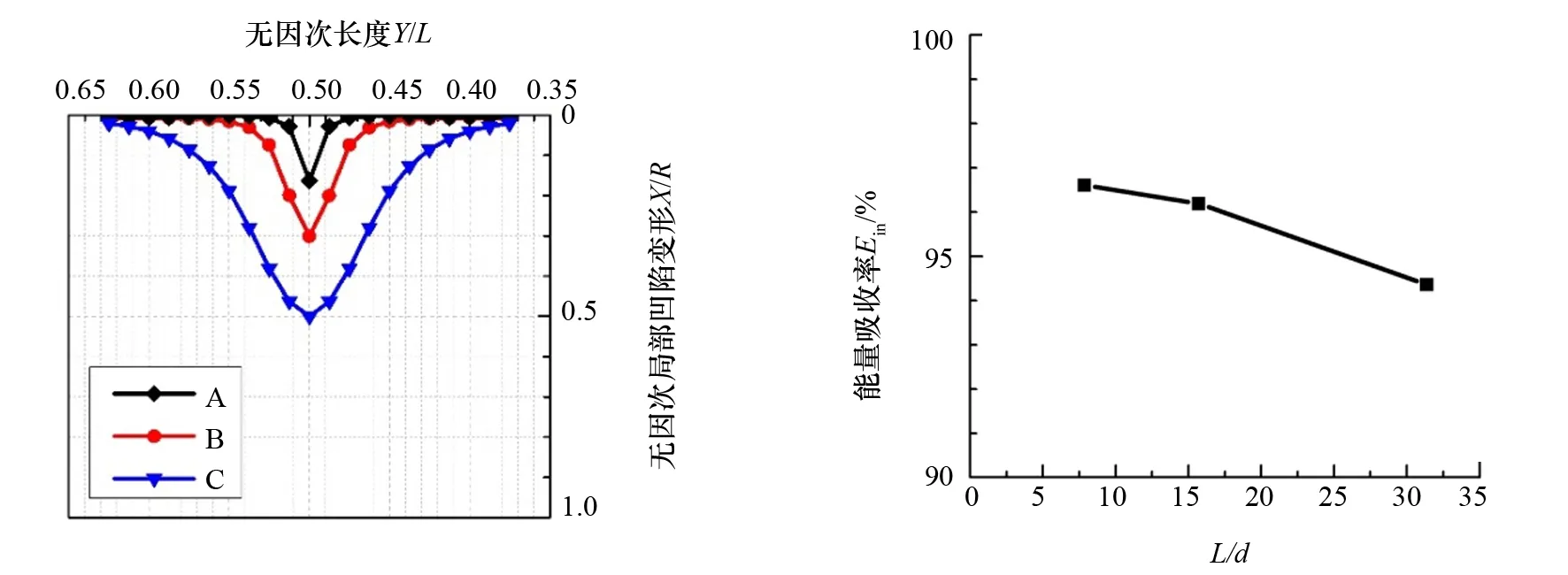
图8 不同L/d下的局部凹陷变形 图9 能量吸收率E in与L/d关系曲线
2.2 d/t的影响
采用与2.1节相同的方法,保持圆管长度L和直径d不变,建立3种不同壁厚t的圆管碰撞模型进行计算,得到相应的碰撞响应过程,具体尺寸如表3所示。

表3 长度和直径不变下圆管构件尺寸汇总
(1) 碰撞力。无因次尺寸参数d/t反映了圆管的径向刚度。由图10可知,在相同的冲击速度条件下,d/t越小,碰撞力越大,撞深则变小。另外,d/t越小,加载阶段弹性振动越明显,碰撞力的波动也越大。
(2) 整体变形与局部凹陷。由图11和图12可知,d/t越大,圆管的径向刚度越小,碰撞后圆管整体变形和局部凹陷变形同时增大。
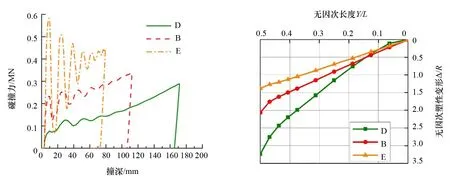
图10 不同d/t下的碰撞力-撞深曲线 图11 不同d/t下的整体变形
(3) 能量吸收情况。由图13可知,在同样的初始动能条件下,能量吸收率Ein随d/t增大而增大,与撞深的变化趋势一致,因此,局部凹陷变形可表征碰撞能量吸收的程度。
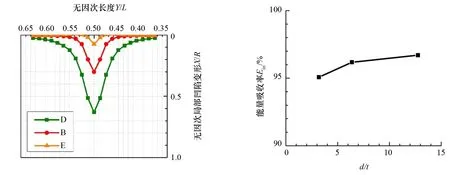
图12 不同d/t下的局部凹陷变形 图13 能量吸收率E in与d/t关系曲线
3 结 语
本文利用LS-DYNA软件对圆管构件受撞击场景进行数值仿真,与模型试验进行对比,验证了模型的有效性,并在此基础上研究圆管几何尺寸参数的改变对圆管结构抗撞性能的影响,得到以下结论:
(1) 圆杆无因次几何尺寸L/d越大或d/t越大,撞击时碰撞反力越小,冲击越缓和。
(2) 碰撞后局部凹陷变形是衡量圆管结构碰撞能量吸收程度的重要指标。
由此可见,基于弹塑性有限元方法的数值仿真技术可为海洋平台圆管构件结构设计与抗撞性能优化提供一种可靠的技术手段。
