创新教育应注重学生思维的引导和开发

朱增成

中图分类号：G622文献标识码：A文章编号：1003-9082（2019）08-0-01

创新教育就是根据创新意识，创新思维、创新能力为主要目标的教育理论，数学课堂教学的创新研究，也逐渐成为许多数学教师关注的话题。由于数学具有应用的广泛性、理论的抽象性和逻辑的严谨性等特点，决定了数学教学不仅是基础教育的组成部分，也是实施创新教育的主阵地。学生在初中階段存在的主要问题是理解难、应用难。这也是各在课教师颇感头疼的问题。究其原因是学生思维的深度和广度不够，所以教师应在学生思维引导和开展上寻找突破口。

一、注重定义、定理的理解、夯实学生思维开发的基础

1.“趣”得定理

由于定理理论的抽象性、推理的独特性， 学生理解较为困难。所以对定理的得到要尽量寻找学生易于观察、易于发现的方法。

例如，在讲授多边形内角和定理时，由四边形内角和定理研究方法：过四边形个顶点作对角线， 可以把四角形分成两个三角形，

可得：四边形内角和=2×180 =（4-2）×1800 =3600

引导：五边形内角和=3×180 =（5-2）×1800 =5400

六边形内角和=4×180 =（6-2）×1800=7200

开发：n边形内角和=（n-2）× 1800

2.“活”解定义

学生在许多题目的解答应用时出错的原因是对定义理解不透好和不灵话而导致，所以看似简单的定义教学也应突出学生题维引导和开发。

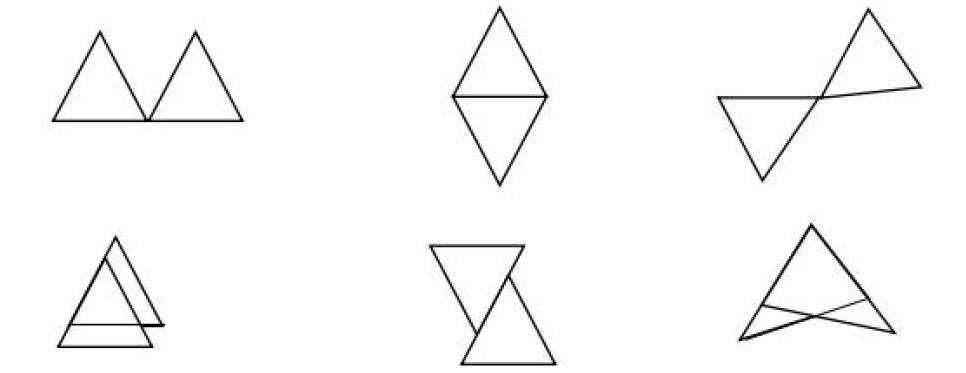
例如：在讲授“全等三角形”定义时，可剪下两个全等三角形，通过如图那样变换两个三角形位置。

进一步抽象成几何图形，让学生找出对应顶点、对应角、对应边，这样可以使学生灵活的掌握全等三角形的全等变换形式，加深学生对全等三角形定义的理解，有助于学生在复杂图形中观察，寻找出全等三角形。

二、注重例题的变形，引导和开发学生思维的深度

教材例题是几何定理的初步应用，学生容易理解，但许多题目木身只是例题的简单变动，学生往往感到束手无策。这说明学生对定理的深度把握不够，所以以例题为切入点， 变换条件和结论，有助于学生思维深度的开发。

三、注重综合，拔高训练，刺激学生思维活力，引导和开发学生思维广度。

几何中的综合拔高训练题是基础知识和基本技能的综合训练，也是学生学习中最困难的地方，但也是具体体现学生思维闪光点和指导开发学生思维的突破口。

例如：已知： AD是△ABC的中线，E是AD的中点，F是BE的延长线与AC的交点。

求证： AF=FC

分析：此题要证AF=FC，但AF与FC

在同一直线上，所以需构造x=FC，再证x=AF即可。

综合分析：平行线等分线段定理推论，可证x=y。

所以方法1：利用平行线等分线段定理推论2构造x =FC。

方法2：利用三角形中位线构造x=FC

此题方法：主要应用等量代换

模式：欲证： AF=FC

需寻找x=FC

x=AF

此题属于由结论证明模式寻找证明方法的题型。

学生感觉综合题、拔高题、应用题等题型困难的主要原因是方法欠缺，以致思维堵塞。所以这类题型应注重方法指导和点拔，由方法找思路，引导和开发学生思维的广度和深度，进而培养学生的创新思维能力。

以上三个方面，遵循了学生由易到难，由简单到复杂，循序渐进的认知规律，突出双基联系，更主要培养了学生思维的灵活性，思维的深度和广度，有力地促进了学生创新思维和创新意识的形成。