培养四种能力,提高复习质量
——关于能力培养的初三数学总复习思考探析
2019-08-31内蒙古北方重工业集团有限公司第一中学王立杰
内蒙古北方重工业集团有限公司第一中学 王立杰
总复习是中考前的特别训练,是学生在学习完初中所有的数学知识后系统地建构自己数学知识框架体系的重要阶段,使学生融会贯通的思维能力达到中考所要求的程度。本文从初三数学知识入手,研究学生在复习中数学技能的培养训练。
一、知识梳理能力
中考总复习首先要做的就是对数学基础概念知识进行一个完整系统的梳理,使学生的脑中能够构建出一个丰满的体系,对知识进行分类归纳,使知识的脉络更加清晰。基础性测试题在中考试卷中占的比重超过60%,这一部分是对学生基础能力的考查。其中的内容包括:数与式、方程与方程式、不等式与不等式组、函数及其图像、统计初步、线与角、三角形、四边形、相似形、解直角三角形、圆。初三这个阶段正是学生查缺补漏的阶段,以往模糊的概念、难以理解的公式经过第一轮的复习应已经一并理清。学生更要清楚每个知识点在试题中所占的比重,要抓住重点,不放过难点,清楚各个知识点之间的联系,提升复习的效率。
二、审题能力
很多学生由于对题目审读不清楚,导致出现一些常见的错误。教师要根据学生出错的点,对学生的错误进行总结归纳。
1.概念不清,审题马虎
一些学生拿到题目便急于套公式,未能将题目的要求以及附加条件或隐藏的条件读出来便立刻上手作答,导致运算思路南辕北辙,答案自然也是错误的。因此,教师在训练的过程中要时时刻刻提醒学生注意审题,不要着急作答。
2.思维固化、漏解
数学公式的运用应是不断变通的,学生看到一道题目应学会用不同的角度思考。
如题:已知A(1,1),B(3,9)是抛物线y=x2上的两点,在y轴上有一动点P,当三角形PAB的周长最小时,P点的坐标是?
解答过程如下:点A(1,1)关于y轴的对称点是C(-1,1),连接BC与y轴的交点就是所求的点P。直线BC的解析式是:y=2x+3,以x=0 代入,得y=3,即所求点P的坐标是P(0,3)。
在这道题目中,一些学生一见到“动点”就不知道该如何下手了,这就要求教师在平常的学习中要培养学生灵活运用公式,读懂出题者的意图,发散思维思考问题,不要僵化教条。
三、数学思维能力
数学思维和数学能力是相辅相成的,数学思维的培养影响着数学能力的提高。因此在研究数学问题时,应注意以下几点:
1.从问题浅显处入手
学生在复习了整个初中阶段所学过的知识后,对解题的模式也不应该只是一问一答,注重思维能力的培养就是在解答后对题目进行进一步的思考,寻求更简单便捷的方法。从概念法则的探究到深入地挖掘规律和本质,数学思维才能逐渐形成,并得到有效的锻炼。
2.从问题发散处入手
数学思维训练的综合性表现在不同的程度和层面上,学生在学习的过程中不要死板地记忆公式,不但要亲自动手推理,还要有举一反三的创新能力。初中数学里有很多公式法则会考验学生的逆向推理,因此教师在日常教学活动中也要注重引导学生进行逆向推理的实践,培养学生从多角度看问题,使其思维空间得到有效的发散。
例如,把抛物线y=ax2+bx+c向左平移2 个单位长度,同时向下平移1 个单位长度后,恰好与抛物线y=2x2+4x+1 重合。求出a、b、c的值,并画出函数的示意图。
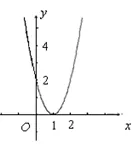
解答过程如下:将y=2x2+4x+1 整理,得y=2(x+1)2-1。
∵抛物线y=ax2+bx+c向左平移2 个单位长度,再向下平移1 个单位长度,得y=2x2+4x+1=2(x+1)2-1,
∴将y=2x2+4x+1=2(x+1)2-1 向右平移2 个单位长度,再向上平移1 个单位长度,即得y=ax2+bx+c,故有:
y=ax2+bx+c=2(x+1-2)2-1+1
=2(x-1)2
=2x2-4x+2,
∴a=2,b=-4,c=2。
本题考查的就是二次函数与几何变换,以上解答过程是将原图像作为出发点。虽然也得出了正确答案,但教师若引导学生逆向探究,会得出新的思路和方法。
四、归纳探究能力
初三的复习不仅是教师在课堂上的一一梳理,学生也应该学会自主地对学过的知识进行归纳整理,在整合的过程中发现共性和规律,以便更好地解答数学题。另外,不要放过综合性强的题目,通过这些题目的锻炼,正是对学生复习结果的一个考验。
如题:在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转。旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图)。
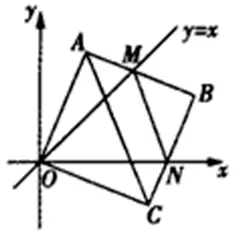
(1)求边OA在旋转过程中所扫过的面积;
(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
(3)设△MBN的周长为p,在正方形OABC旋转的过程中,p值是否有变化?请证明你的结论。
这一类型的题对学生的空间想象、推理以及创新能力都是一种考察,将实践操作与理性思考相结合。图形变化中变与不变是学生思考的关键点,学生在一步步的思考中,不但能在脑中将已学过的知识进行汇总和联系,还能逐步地锻炼探究能力。
通过发展以上所述的四种能力,有助于培养学生的思考探究能力,形成良好的思维体系,对他们未来的中考甚至高中阶段的学习都有莫大的帮助。
