挖掘教学资源,提升初中数学复习课效率
2019-08-31上海民办华东师大二附中紫竹双语学校夏红波
上海民办华东师大二附中紫竹双语学校 夏红波
上好一堂复习课绝非易事,需要做很多的课前准备设计工作,教师要带着思考,结合知识,融入方法,选择适合学生并能更好地调动学生自主学习的教学方法,认真准备编辑复习课内容,不断提高复习课的教学质量,以达到最佳的复习效果。
一、开放资源,点燃学生热情
复习课要通过充分设计让学生积极参与和思考,而问题的开放性能较好地充当复习课的润滑剂,能让学生的主体地位得以充分体现,点燃学生热情。如《锐角三角比》的复习课可以开放设问,教师的情景引入如下:
1.在Rt △ABC中,∠C=90°,sinA=,BC=8,你可以获得哪些结论,依据分别是什么?
2.在△ABC中,sinA=,AC=6,BC=8,你可以获得哪些结论,依据分别是什么?
3.在△ABC中,AB=AC=13,BC=10,你可以获得哪些结论,依据分别是什么?
4.在△ABC中,∠A=60°,∠B=45°,AB=8.你可以获得哪些结论,依据分别是什么?
该片段通过开放设问方式,让不同层次的学生思维都活跃起来,积极参与,主动探究、回忆、归纳。以上四个开放性问题的编排潜藏了思想和方法,学生在主动探究的过程中获得了能力。
二、整合资源,促进学生思维
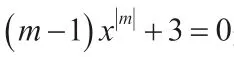
三、变式资源,锻炼学生能力
在复习阶段如果仅仅是简单的知识梳理,然后就进行大量的习题练习,这样易让学生心烦,学习效率低下,能力得不到发展。依据教材和概念的核心进行资源变式,可以增强学生的思辨力,进而在复习课中使能力得到锤炼与提升。
例1:如图1,在等边三角形ABC的边BC上任取一点D,以CD为边向外作等边三角形CDE,连接AD、BE,试说明BE=AD的理由。
变式1:如图2,已知点B、C、E在一条直线上,△ABC、△DCE都是等边三角形,连接AE、BD,试说明△AEC、△BCD全等的理由.
变式2:如图3,已知点B、C、E不在一条直线上,△ABC、△DCE都是等边三角形,连接AE、BD,试说明BD=AE。
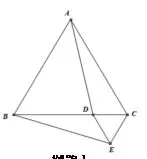
图1
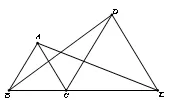
图2
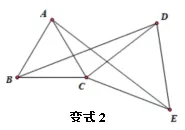
图3
通过几道类似题目的设计,帮助所有学生体会感悟,在精讲和精练中学生都有所收获,形成初步的解题方法和技巧。在初中数学复习课中,教师要做的不是一题题的呈现和众多练习题的堆砌,而是结合学生情况挑选教学资源进行有效变式,提炼问题的精华,这样学生的理解能力和感悟能力得到锻炼,复习效果事半功倍。
四、化归资源,提高学生素养
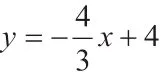
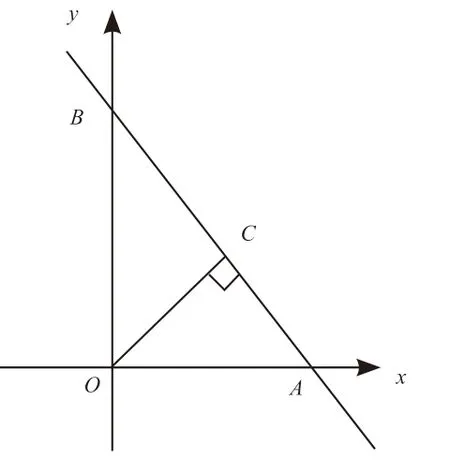
分析:该习题是一道典型的点坐标的求法问题,通过知识的转化方向不同,就会出现不同的解题方法,解法如下:
1.运用两点间的距离公式求
若将垂直转化为三角形的高,则可以用等面积法算出OC长来进行解答:
2.运用函数交点求
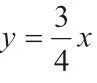
3.运用点坐标定义求
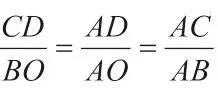
此类问题都是化归思想的运用,化归资源将“未知”转化为“已知”,其核心就是将有待解决的问题转化为已有明确解决程序的问题,以便利用已有的理论、技术来加以处理,从而培养学生用联系、发展、运动变化的观点观察事物,认识问题。有了这些,学生才能真正做到聪明学习,减负增效。
