一种提高数模混合仿真系统稳定性的算法研究
2019-08-30赵艳军安然然张远
赵艳军,安然然,张远
(广东省智能电网新技术企业重点实验室(广东电网有限责任公司电力科学研究院),广东 广州 510080)
电力系统仿真包括全数字仿真、物理仿真和数字物理混合仿真(数模混合仿真)。数模混合仿真需要通过功率型数模连接装置进行数字侧和物理侧的无缝对接,而采用不同的接口算法所开发的连接装置适用范围、稳定性和可行性不同[1-8]。国内外现有的数模混合仿真接口装置均处于研究阶段[9-11],没有统一标准,研究中常用的算法主要有理想变压器法[12]、输电线路模型(transmission line model,TLM)法[13]、电路分割法[14]、时变一阶近似法[15]和阻尼阻抗法[16],有学者对比分析了不同算法的准确性和稳定性[17]。
对比发现,基于理想变压器模型算法的功率连接装置易于开发实现;但通过算法稳定性分析发现,该算法具有一定的适用要求,即数字侧等值阻抗恒定小于(或者大于)物理侧等值阻抗。而数字侧和物理侧模型由于故障或网络拓扑结构变换导致等值阻抗改变时,系统稳定条件将被破坏,针对该问题尚无文献提出解决措施。对此,本文研究了一种基于阻抗补偿的数模混合仿真接口算法,提出在仿真过程中可能存在稳定条件破坏的情况下,通过在物理侧和数字侧分别进行阻抗补偿,从而保持数模混合仿真系统稳定运行。
1 数模混合仿真接口模型及稳定性分析
1.1 理想变压器模型
在任一具有唯一解的电路中,若支路k的电压和电流分别为Uk和Ik,且支路k与电路的其他部分之间无耦合联系,则可以用一个电压等于Uk的电压源或电流等于Ik的电流源来替代该支路。
在数模混合仿真系统中,通常情况下所选择的数模接口处支路与其他电路之间不存在耦合关系。根据上述替代定理,为实现数字系统和物理系统的柔性连接,可采用以下2种方式:一是理想变压器模型1,以理想电压源模型替代数字接口处的电压作为物理侧接口支路,同时以理想电流源模型替代物理接口处的电流作为数字侧接口支路,原理如图1所示;二是理想变压器模型2,以理想电流源模型替代数字接口处的电流作为物理侧接口支路,同时以理想电压源模型替代物理接口处的电压作为数字侧接口支路,原理如图2所示。

图1 理想变压器模型1
图1中,E1为数字仿真系统的等值电势,Z1为数字系统等值阻抗,E2为物理仿真系统的等值电势,Z2为物理系统等值阻抗,U1为数字系统接口电压,U2为物理系统接口电压,i1为数字系统接口支路电流,i2为物理系统接口支路电流。U2受U1控制,i1受i2控制。

图2 理想变压器模型2
图2中,U1受U2控制,i2受i1控制。
1.2 数模混合仿真的物理实现
理想变压器模型算法简单,容易实现,因而该模型在国内外数模连接接口实验研究中经常使用。如图3所示,通过D/A转换和数模连接器(该装置为四象限功率放大元件)可将数字侧接口支路的实时离散数字信号反映到物理侧,通过A/D转换则可将物理侧接口支路的实时连续模拟信号反映到数字侧,最终实现数字、物理混合仿真。
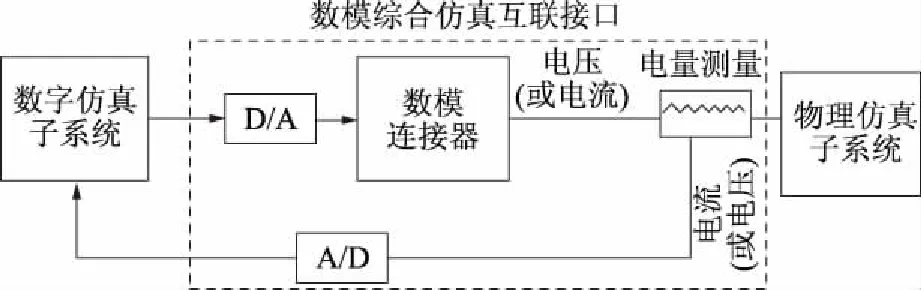
图3 数模混合仿真互联接口示意图
从数学角度而言,物理仿真和数字仿真是完全统一的,它们都是使本身的系统和模拟的系统之间在数学上满足相同的微分-代数方程组。但二者的具体实现方式不同,物理仿真采用物理元件模拟真实系统,以元件运行特性为基础,持续运行于自然物理状态,属于连续域;而数字仿真则是通过数字离散化实时求解微分-代数方程,属于时间离散域。
以理想变压器模型1为例,按照时间顺序,数模混合仿真的动态交互过程包括以下几个步骤:
a)以数字仿真第m个周期运行完毕为起始时刻算起,假设此时时间为tm,数字接口支路电压为u1(tm)。
b)采集tm时刻数字接口支路电压u1(tm),该信号经A/D转换和信号传输传递给数模连接装置,经功率放大后作用于物理系统;假设该阶段所用时间为Δt1,忽略数模连接装置及信号传递过程中引入的误差,则此刻物理系统接口支路电压被受控电压源控制为u2(tm+Δt1)=u1(tm)。
c)假设从tm+Δt1至采集物理系统接口支路电流的时间间隔为Δt2,此刻物理系统接口支路电流为i2(tm+Δt1+Δt2)。
d)物理系统接口支路电流采集值将通过A/D转换上传至实时数字仿真仪(real time digital simulator,RTDS),假设所用时间为Δt3,忽略信号采集及传递过程中引入的误差,则此刻物理系统接口支路电流被受控电流源控制为i1(tm+Δt1+Δt2+Δt3)=i2(tm+Δt1+Δt2)。
e)在(m+1)T(T为数字仿真部分的计算步长)时刻时,数字仿真系统在物理侧返回的受控电流源i1(tm+Δt1+Δt2+Δt3)的作用下,进行迭代计算,从而完成1次数模混合迭代计算,并进入下个周期的循环。
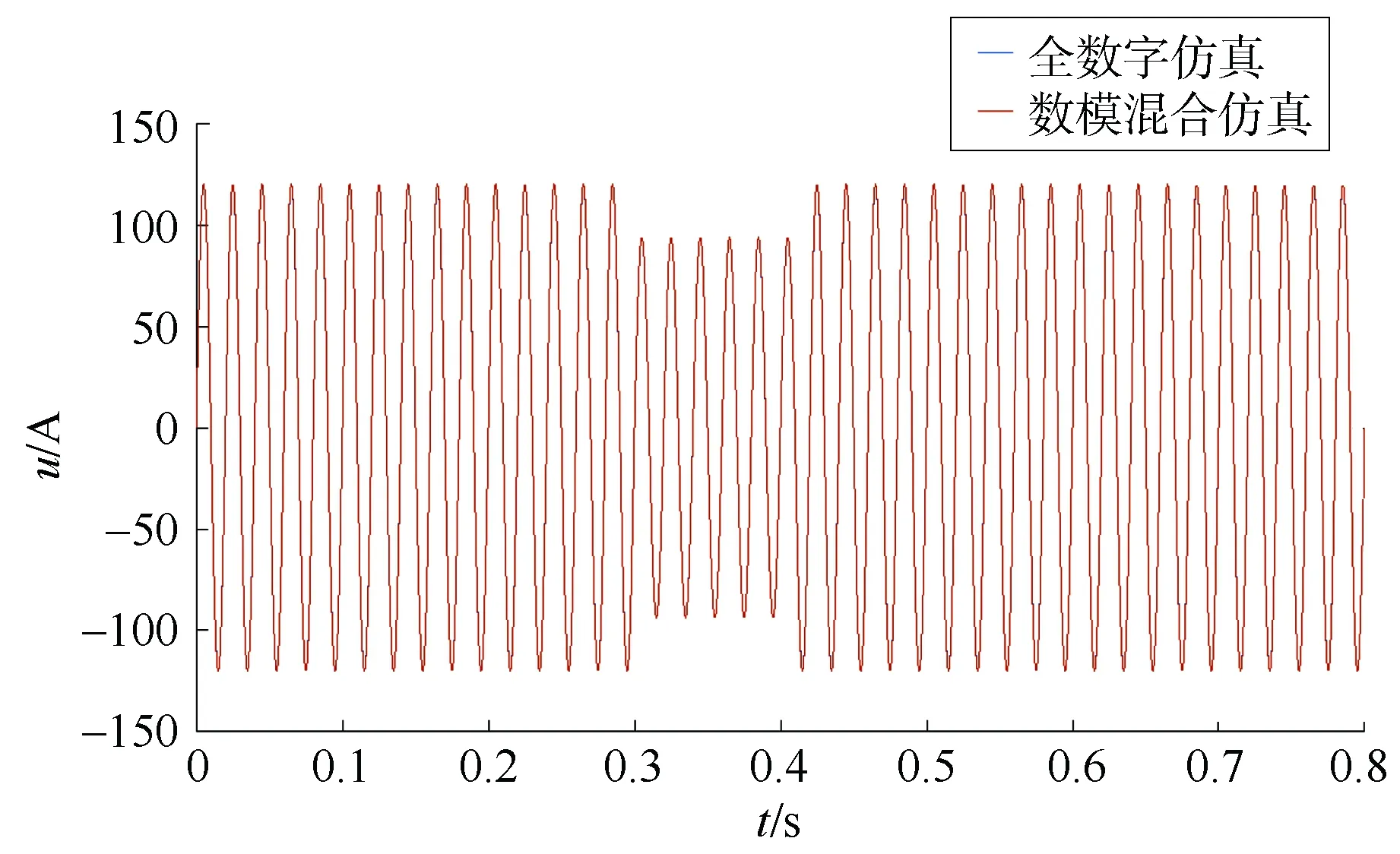
上述过程中,Δt1、Δt2、Δt3为固有时间,与数模混合仿真不同环节的物理装置响应时间常数相关。为了减少误差,通常情况下在开发数模混合仿真接口装置时要求Δt1+Δt2+Δt3 由分析可知,物理系统接口电压滞后数字系统接口电压时间为Δt1,数字系统接口电流滞后物理系统接口电流时间为T-(Δt1+Δt2),且T>Δt1+Δt2。 数模混合仿真系统框图如图4所示,其中τ1=Δt1,τ2=T-(Δt1+Δt2),s为频域算子。 图4 数模混合仿真系统框图 数模连接器接口算法的选择直接影响数字、物理系统是否稳定运行,因而系统稳定性是评估数模连接装置可行与否的首要指标。以理想变压器模型1为例,分析该系统的稳定性及适用情况。 假设所研究的原系统本身稳定(如图4所示),若数模混合仿真系统稳定,则要求系统闭环特征方程的所有根实部均为负值。该系统的开环传递函数 根据乃奎斯特稳定判据,当开环传递函数右半平面没有极点时,系统闭环稳定的充要条件是开环幅相频率特性曲线不包围临界点(-1,j0)。GOL在右半平面上没有极点,且是以原点为圆心,以Z1为半径的圆,若要求系统闭环稳定,则需 由上述分析可知,采用理想变压器模型1时,系统闭环稳定的条件是Z1 由第1.3节分析可知,数字系统和物理系统等值阻抗变化时,需采用不同的理想变压器模型,才能保证系统稳定。原则上数字侧搭建的系统规模远大于物理侧搭建的系统模型,满足数字侧等值阻抗小于物理侧等值阻抗的条件,因此在一般情况下采用理想变压器模型1。但在某些特殊的情形下,比如物理侧接近数模混合仿真接口装置出口处短路,若仍然采用理想变压器模型1,系统不能稳定运行,需要采用切换接口算法的方法切换到理想变压器模型2。切换方案虽然可行,但在数模混合仿真接口实现起来较复杂,本文考虑了方法实现的可行性,提出基于阻抗补偿的数模混合仿真算法。 阻抗补偿算法的基本思路是:在采用理想变压器模型1作为接口模型的条件下,当数字侧阻抗大于物理侧阻抗时,在数字侧添加负阻抗,在物理侧添加等值的正阻抗,补偿阻抗值大小需保证数字侧整体等效阻抗小于物理侧整体等效阻抗,此时理想变压器模型1仍满足稳定条件。基本原理图如图5所示,其中ΔR为补偿的正电阻、ΔL为补偿的正电感、-ΔR为补偿的负电阻、-ΔL为补偿的负电感、Δu为补偿阻抗之后的电压。 图5 阻抗补偿算法基本原理 然而,在稳定条件破坏的情况下,采集运行数据、判断是否投入补偿阻抗、执行阻抗补偿均需要一定的时间,在未投入补偿阻抗之前,系统电磁暂态仿真可能已经发散,这对阻抗补偿的快速性要求非常高。在实际仿真中,仿真之前系统等值参数、故障集均已知;因而考虑方案的可行性,针对部分故障可能导致系统稳定条件破坏的情况,可提前计算补偿阻抗的大小,且在开始仿真前投入补偿阻抗,保证故障前、后均满足稳定条件,且故障后不用再进行即时阻抗补偿。 针对提出的阻抗补偿算法,利用MATLAB进行仿真验证。在MATLAB中搭建数模混合仿真系统的数字仿真子系统、物理仿真子系统以及接口装置,用延时环节来模拟实际混合仿真系统由于数模接口算法所导致的延时,本文采用纯电阻电路。 首先搭建如图6所示仿真电路,(a)为全数字仿真电路,作为对比;(b)为数模混合仿真系统,左侧为数字侧系统,右侧为物理侧系统,接口采用理想变压器模型1。其中,数字侧电阻R1>物理侧电阻R2,但是在添加了补偿电阻R后,保证了数字侧总体等值电阻(R1-R)小于物理侧总体等值电阻(R2+R)。 图6 简单电路示意图 考虑一定的采样保持和接口延时,图7、图8给出了相应的物理侧电流、电压波形,并与全数字仿真进行对比。 图7 全数字和数模混合仿真中,物理侧电流波形对比 图8 全数字和数模混合仿真中,物理侧电压波形对比 由图7和图8可见,加入补偿电阻的系统可以保持稳定,并且仿真得到的电压、电流波形与没有互联接口的全数字仿真波形基本重合。互联接口延时环节的加入,导致电压、电流波形有一定的相位差。接下来验证暂态过程中采用补偿阻抗算法的可行性,拟采用如下方案。 搭建图9所示的电路图,其中(a)为全数字仿真,(b)为采用阻抗补偿算法的数模混合仿真系统,左侧为数字子系统,右侧为物理子系统。图9(a)中,R1=5 Ω,R2=3 Ω,R3=7 Ω,其中A点为暂态过程中的短路接地点,B点为数字仿真系统和物理仿真系统的连接点,故障设置形式为0.3 s时A点接地,0.4 s时故障切除。 图9(b)中,R1=5 Ω,R2=-2 Ω,R3=2 Ω,R4=3 Ω,R5=7 Ω,故障设置形式与图9(a)相同。图9(b)中,若没有采用阻抗补偿,数字侧等值阻抗为5 Ω,物理侧等值阻抗为10 Ω,稳态运行时满足稳定运行条件;故障期间,数字侧等值阻抗仍为5 Ω,物理侧等值阻抗变为3 Ω,系统将失去稳定。故在仿真前在数字侧补偿-2 Ω、物理侧补偿2 Ω,使得正常运行和故障期间,数模混合仿真系统总能满足稳定运行条件。 图9 动态过程简单电路图 图10和图11给出了全数字仿真和数模混合仿真的电流、电压对比波形。 图10 全数字仿真和数模混合仿真的电流波形 图11 全数字仿真和数模混合仿真的电压波形 由仿真结果可知,暂态故障前后,系统均能保持稳定运行,全数字仿真与数模混合仿真结果基本吻合。 综上所述,阻抗补偿算法可行。同理,若数模混合仿真接口采用理想变压器模型2,当仿真中存在稳定条件破坏的情况,采用本文提出的阻抗补偿算法时,需要在数字侧补偿正阻抗,在物理侧补偿等值的负阻抗,才能满足稳定运行条件。考虑到物理侧补偿负阻抗,通常需要通过电力电子装置实现,实现过程复杂。本文建议在这种情况下,调整接口位置,在初始状态时接口就选择理想变压器模型1,并进一步在数字侧补偿负阻抗、在物理侧补偿正阻抗,可保证故障前后系统均能保持稳定。 数模混合仿真系统中,接口模型采用理想变压器模型1时,需满足数字系统等值阻抗小于物理系统等值阻抗,才能保证系统稳定运行。但当数字系统等值阻抗大于物理系统等值阻抗时,本文提出一种阻抗补偿算法,在数字系统补偿负阻抗,在物理系统补偿等值的正阻抗。仿真结果表明,在稳态和暂态情况下,该补偿算法均有效可行。
1.3 稳定性分析

2 阻抗补偿算法

3 仿真验证





4 结束语
