一种新型剁式悬臂挡土墙特征分析

2019-08-30邵先锋杨泰朋朱克亮

土木工程与管理学报 2019年4期

邵先锋，杨泰朋，朱克亮

(1.国网安徽省电力有限公司建设分公司，安徽合肥 230022；2.安徽送变电工程有限公司，安徽合肥 230022)

在山区的公路、铁路及其它工程建设中，往往需要使用挡土墙来支承路基填土或山坡土体，防止填土或坡体发生过大的变形或失稳。常见的挡土墙为单级挡土墙[1～5]，即挡土墙从墙顶到墙脚为连续分布的整体结构。

在某些特殊情况下，也可采用二级甚至多级垛式挡土墙。刘文治等[6]对高填土边坡多级挡土墙土压力进行了观测试验研究，结果表明多级挡土墙墙后水平土压力随着上部填土高度沿着墙高呈非线性分布,不能把单级挡土墙的设计理论简单地应用于多级挡土墙；范瑛[7]针对在湖北段某高速公路的实际多级挡土墙工程情况，釆用现场原型试验、室内试验、理论分析、数值模拟相结合的手段对该多级挡土墙进行土压力及变形研究；王景环等[8]基于土的塑性极限分析理论，研究了二级新型悬臂式挡土墙土压力受力分析模式，给出了土压力强度、土压力合力、土压力作用点的理论计算公式；张勇等[9]通过有限元方法计算出填土在不同内摩擦角、黏聚力取值下挡土墙的应力-应变关系的变化趋势，揭示了边坡形成整体滑移破裂面而导致多级悬臂式挡土墙失稳的机理；梁桥等[10]通过理论解析及实例分析表明二级悬臂式挡墙基底应力分布比单级悬臂式挡墙更合理，也更偏向于安全；贾喜翠等[11]对二级悬臂式挡土墙的抗震性能进行探讨，结果表明二级悬臂式挡土墙克服了单级悬臂式挡墙限制高度的缺点，增强了挡墙的抗滑和抗倾覆稳定性。这些研究成果增进了人们对多级挡土墙土压力与稳定性的了解。

但传统的二级(或多级)剁式挡土墙中，上一级挡土墙仅压在下一级挡土墙墙背的填土上，上、下级挡土墙之间无直接荷载传递作用，上、下级挡土墙之间缺乏有效的相互连接，如图1所示。

图1 常见的二级剁式挡土墙结构

若能够设计一些辅助构件，使上、下挡土墙之间直接传递部分荷载，可能对挡土墙的整体稳定性有正面作用。因此，本文提出一种新型剁式挡土墙结构，并基于有限元方法对其土压力、填土变形及稳定性进行对比分析，为二级(或多级)剁式挡土墙的合理设计提供一定的参考。

1 有限元计算模型

传统的二级(或多级)剁式挡土墙中，上一级挡土墙压在下一级挡土墙墙背的填土上，即上一级挡土墙的部分荷载通过填土传递作用于下一级挡土墙，相邻挡土墙之间并不直接传递荷载。可见，传统的二级(或多级)剁式挡土墙中，上、下级挡土墙不发生直接作用，本质上相互独立，整体性相对较差。

为此，本文提出一种新型剁式挡土墙，各级挡土墙为钢筋混凝土结构，在下墙顶部的填土侧设置一个支墩，上墙的墙趾板沿竖向压在支墩上。支墩的宽度通常不大于1.0 m。下墙设置支墩后，所提剁式挡土墙具有下列特征：

(1)上、下级挡土墙在制作与施工过程中均相互独立，互不影响；

(2)施工时，仅把上墙的墙趾板搭在下墙的支墩上方，上、下级挡土墙之间本质上是相互分离的；

(3)上级挡土墙承担的部分竖向荷载，可通过支墩直接传递给下级挡土墙，但上、下级挡土墙之间不传递水平荷载(或剪力)；

(4)由于上、下级挡土墙之间通过支墩直接接触，使得上、下级挡土墙的变形与变位将相互牵制与影响。

现针对某一设置支墩的二级垛式挡土墙进行分析，上、下两级挡土墙尺寸基本相同，挡土墙高度H=5 m、墙踵板长度L=3.5 m，下级挡土墙顶部附近设置宽度1.0 m的支墩，钢筋混凝土板厚50 cm，挡土墙的计算构型如图2所示。

图2 新型二级剁式挡土墙计算构型

采用平面应变有限元进行分析。原地基与填土材料采用Mohr-Coulomb理想弹塑性模型，挡土墙为钢筋混凝土结构，其强度较高，可按线弹性材料考虑。各土层及挡土墙的物理力学参数见表1。

表1 各土层及挡土墙的物理力学参数

为了模拟挡土墙与土体之间的界面特性，可在两者之间设置无厚度的接触面单元。采用摩擦系数R来反映挡土墙与土体之间的相互作用程度，根据相关文献的实验数据[2]，并结合墙后土体的物理力学参数，本次计算中取R=0.65。

数值计算的边界条件为：底部采用固定边界条件(不发生水平位移和竖向位移)，两侧为水平方向位移约束条件。采用15节点的三角形单元对计算模型进行网格划分，并在挡土墙与填土接触的部位及土层分界面加密网格划分，图3给出了有限元网格的划分情况(2870个)。

图3 有限元网格划分

原地基土的沉降在挡土墙施工前早已完成，可通过逐步激活挡土墙与填土单元来模拟各施工工序，并采用强度折减有限元法[12～14]来考察挡土墙的滑裂面位置及安全系数。

2 计算结果分析

基于有限元方法，对不同参数情况下的二级剁式挡土墙土压力与填土变形进行了考察，得到了新型二级剁式挡土墙的基本特征。

2.1 填土变形特征

施工结束后，墙后填土内部的侧向位移等值线分布如图4所示，填土内部的竖向沉降如图5所示。图4中的负值表示侧向位移与x轴方向相反。

图4 填土内部侧向位移等值线分布/cm

由图4可知，下墙范围内填土的侧向位移向临空面方向发展，具有向临空面旋转倾覆的趋势，其与传统的单级悬臂式挡土墙规律相同。

上墙底板置于新填土中，底板上的填土自重压在底板上，使得底板与上、下方填土一起发生变形。特别地，由图5可知，底板长度范围内的竖向沉降不均匀，靠近临空面一端底板的竖向沉降小，而远离临空面一端底板的竖向沉降大，即上墙发生了沿逆时针方向偏转，从而导致上墙上部局部范围内填土的侧向位移向临空面反方向发展，且最大侧向位移发生在上墙顶部附近的填土中。

图5 填土内部竖向沉降等值线分布/cm

未设置支墩时，填土内部的最大侧向位移为-1.4 cm；下墙顶部设置支墩后，填土内部的最大侧向位移为-3.5 cm，即设置支墩后填土的侧向位移最大值变大。这是由于设置支墩后，底板的右端部(即墙趾板)被支墩牵制与约束无法发生较大的竖向沉降，迫使上墙底板产生较大的不均匀沉降，即上墙沿逆时针方向偏转幅度更大，故上墙顶部向填土侧发生的侧向位移较大。

由图5可知，设置支墩与否对填土内部的竖向沉降影响不明显，这是由于土体竖向沉降主要由土体自重产生，而设置支墩与否对土体自重无影响。

2.2 挡土墙土压力特征

2.2.1 侧向土压力

新型二级剁式挡土墙下墙立板受到的侧向土压力特征如图6所示，具体侧向土压力值如图7所示。未设置支墩时，下墙立板受到的侧向土压力最大值为76.5 kPa；下墙顶部设置支墩后，下墙立板受到的侧向土压力最大值为58.9 kPa；侧向土压力最大值均位于下墙的底部附近。设置支墩后，下墙受到的侧向土压力明显变小，大大提高了下墙的抗倾覆承载力。

图6 下墙立板受到的侧向土压力特征

图7 下墙立板受到的侧向土压力

上墙立板受到的侧向土压力如图8所示。可见，下墙顶部设置支墩后，上墙受到的侧向土压力值明显增大。进一步分析知，上墙受到的侧向土压力最大值为35.0 kPa，约为下墙侧向土压力最大值的一半，即上墙受到的土压力总体上远小于下墙的侧向土压力。挡土墙受到的侧向土压力越大，其截面面积越大，故下墙的截面尺寸应远大于上墙的截面尺寸，增加了下墙的施工难度。

图8 上墙立板受到的侧向土压力

可见，下墙顶部设置支墩后，下墙受到的侧向土压力明显减小，而上墙受到的侧向土压力明显增大。设置支墩后，下墙原本较大的侧向土压力值大大变小，上墙原本较小的侧向土压力值有所变大，下墙与上墙的侧向土压力得到了合理的转移与重分配，使下墙与上墙的截面尺寸相差较小，降低了整体施工难度，显然是有利的。

下墙原本较大的侧向土压力值大大变小，使得下墙的抗倾覆稳定性大大提高。虽然上墙的侧向土压力值有所增加，但由于其数值相对较小，增加后的上墙侧向土压力仍小于下墙的侧向土压力，故挡土墙的整体抗倾覆稳定性仍由下墙控制。可见，上墙侧向土压力的增加并不会恶化整体的抗倾覆能力，而下墙侧向土压力的减小则大大提高了整体的抗倾覆稳定性。故下墙顶部设置支墩后，二级剁式挡土墙的抗倾覆稳定性整体上将有提高。

2.2.2 竖向土压力

下墙底板上部受到的竖向土压力如图9所示。可见，下墙顶部设置支墩后，下墙底板上部受到的竖向土压力值变小。上墙受到的部分竖向荷载已通过支墩基于下墙传递给了下墙底部的原地基，转移了部分竖向荷载，从而降低了下墙底板上部的竖向土压力。

图9 下墙底板上部受到的竖向土压力

下墙底板底部受到的竖向应力如图10所示，该应力由填土自重、上、下级挡土墙的自重产生。可见，下墙底板底部受到的竖向应力呈非线性分布，在墙趾板附近的竖向应力较大，而墙踵板末端的竖向应力较小。未设置支墩时，下墙底板底部受到的最大竖向应力为483.2 kPa，最小竖向应力为104.9 kPa。下墙顶部设置支墩后，下墙底板底部墙趾板附近的最大竖向应力进一步增大，而墙踵板末端的最小竖向应力进一步减小，应力集中现象更显著。这是由于设置支墩后上墙的部分竖向荷载基于支墩传递给了下墙，导致下墙立板底部附近的竖向应力进一步增大。

图10 下墙底板底部受到的竖向应力

上墙底板上部受到的竖向土压力如图11所示，可见，下墙顶部设置支墩后，上墙底板中部偏左的底板上部受到的竖向土压力值变小，而上墙底板中部偏右(墙趾板一侧)的底板上部受到的竖向土压力值与未设置支墩时的竖向土压力基本相同。下墙顶部设置支墩后，上墙具有绕支墩向填土侧旋转的趋势，故上墙底板左端部产生的竖向沉降更大，约束填土竖向变形的能力减弱，因而上墙底板左端部受到的竖向土压力值变小。

2.3 挡土墙的抗滑稳定性

基于强度折减有限元法来计算二级剁式挡土墙的抗滑稳定性。其操作步骤为：在有限元计算中，首先对于某一假定的强度折减系数Ftrial，将各土层的原始强度参数粘聚力c与内摩擦角φ按下式同时折减：

(1)

式中：cr，φr分别为折减后黏聚力与内摩擦角。以此对边坡进行弹塑性有限元计算，如果根据一定的失稳判据[12～14]确定边坡达到极限平衡状态，则与此相对应的强度折减系数Ftrial就是挡土墙安全系数Fs，否则对于新假定的折减系数重复计算，直至土体达到临界极限平衡状态。

计算得到了二级垛式悬臂式挡土墙滑裂失稳时滑裂面的位置，如图12所示。可见，填土中有两个滑裂面，第一滑裂面基于下墙墙踵板根部贯穿于填土中，第二滑裂面基于上墙墙踵板根部贯穿于上部填土中。

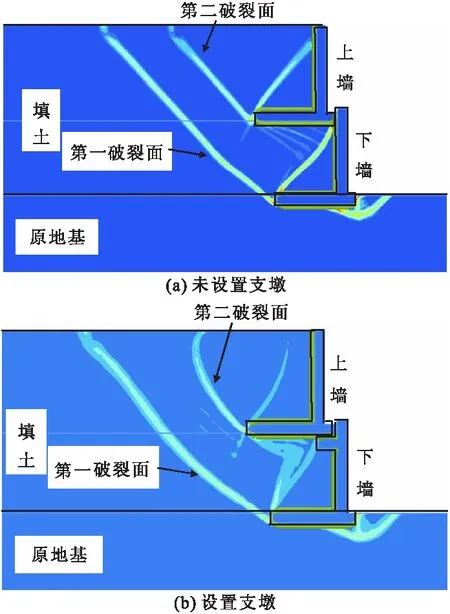
图12 挡土墙抗滑破裂面的分布

未设置支墩时，二级剁式悬臂挡土墙的安全系数为1.83；设置支墩后，二级剁式悬臂挡土墙的安全系数为2.10。可见，设置支墩对提高挡土墙的稳定性有帮助。结合上述挡土墙侧向土压力规律可知，设置支墩后下墙原本较大的侧向土压力值逐渐变小，上墙原本较小的侧向土压力值有所变大，下墙与上墙的侧向土压力得到了合理的转移与重分配，从而提高了由下墙控制的整体抗滑(即第一破裂面)稳定性强度。

图13进一步给出了设置与未设置支墩情况下挡土墙滑裂破坏时单元网格变形情况。可见，设置支墩对下墙的滑裂破坏基本无影响，但对上墙的影响较大。未设置支墩时，挡土墙滑裂破坏时上墙有向临空面倾覆的趋势；设置支墩后，上墙有绕支墩向填土侧旋转滑裂破坏的趋势。

图13 挡土墙抗滑破坏时单元网格变形情况

上墙底板长度3.5 m，设置支墩时，下墙底板长度对挡土墙抗滑稳定性的影响如图14所示。下墙底板长度为2.5 m时挡土墙的抗滑安全系数为1.89，下墙底板长度为4.5 m时挡土墙的抗滑安全系数为2.34，挡土墙的抗滑安全系数随着下墙底板长度的增加呈线性增加的规律。图15进一步给出下墙底板不同长度时滑裂面的分布情况，可见，下墙底板长度越大，第一滑裂面的长度越大，因而抗滑稳定性越高。

图14 下墙底板长度对挡土墙抗滑稳定性的影响

图15 下墙底板长度对抗滑破裂面的影响

下墙底板长度3.5 m，设置支墩时，上墙底板长度对挡土墙抗滑稳定性的影响如图16所示。上墙底板长度为2.5 m时挡土墙的抗滑安全系数为2.05，上墙底板长度为4.5 m时挡土墙的抗滑安全系数为2.14，可见上墙底板长度变化对挡土墙的抗滑稳定性影响可忽略不计。由于挡土墙的整体抗滑稳定性由第一滑裂面控制，上墙底板长度变化对第一滑裂面的位置及长度不产生影响，故上墙底板长度对抗滑稳定性基本无影响。