基于频漂校准的氢钟铯钟联合守时研究

刘阳,彭竞,龚航,胡旖旎,欧钢

(1.国防科技大学 电子科学学院,湖南 长沙 410073; 2.北京跟踪与通信技术研究所,北京100094)

0 引 言

守时实验室通过建立溯源链路将本地时间和远端高标准时间比对,依据比对结果调整本地时间,进而使本地时间同步到远端高标准时间上,达到维持本地时间稳定、准确的目的[1-2]. 然而,在部分守时实验室没有外部溯源链路或者溯源链路失效的情况下,需要本地钟组自主守时,维持本地时间的稳定和准确. 这对本地钟组和自主守时算法提高了要求.

原子时算法分为两大类:加权平均算法和卡尔曼滤波算法. 加权平均算法主要包括:国际权度局(BIPM)采用的ALGOS算法[3-6]、美国国家标准与技术研究院(NIST)采用的AT1算法[7-8];卡尔曼滤波算法,主要包括:NIST在20世纪80年代使用的标准Jones-Tyron 型卡尔曼滤波算法,和在此基础上改进得到的一系列卡尔曼滤波算法[9]. AT1算法和卡尔曼滤波算法生成的时间尺度是实时的,适用于实验室守时.

目前,守时实验室用于守时的原子钟主要包括铯钟和氢钟. 不同类型的原子钟在时间保持中有各自的优势[10]. 铯钟是发展较早的一种原子钟,由于其优良的长期稳定度性能,过去一直作为主要的守时原子钟. 然而,其不足在于短期稳定度较差. 氢钟是近年来新发展起来的一种原子钟,由于其优良的短期稳定度,以及其各项指标的不断提升,逐渐作为新型的原子钟参与守时. 其不足在于长期稳定度较差,而且频率漂移较大[11].

针对上述现状,研究氢钟铯钟联合守时算法有一定的实际意义. 有论文对此进行过研究:文献[10]利用氢钟短期稳定度好的特点,用作测量铯钟噪声的参考,对铯钟噪声滤波建立时间尺度. 文献[12]对铯钟扣除频差,氢钟扣除频差和频漂后,加权平均计算综合原子时驾驭氢钟. 文献[13]通过小波变换对氢钟滤除噪声,用氢钟和铯钟生成时间尺度. 文献[14]研究了铯原子喷泉钟驾驭氢钟的预估算法.

以上氢钟铯钟联合守时研究中,在注重短期稳定度的场合,由于加权平均算法中对于取权方式的选择,往往导致氢钟权重较大,而铯钟权重较小,铯钟的长期稳定度性能没有充分发挥.针对这一问题, 本文提出一种新的综合利用铯钟和氢钟的方案:利用铯钟数据通过卡尔曼滤波计算氢钟频漂并且对氢钟频漂校准,基于铯钟数据和频漂校准后的氢钟数据,利用单状态变量卡尔曼滤波生成本地原子时,在保持原子时短期稳定度的前提下,提高其长期稳定度性能.这对于守时实验室自主守时情况下,维持本地时间的长期稳定度性能具有意义.

1 氢钟铯钟特性分析

1.1 原子钟模型

铯钟模型[15]:

x(t)=x0+y0t+xr(t).

(1)

氢钟模型:

x(t)=x0+y0t+0.5at2+xr(t).

(2)

式中:x0为初始时刻相位偏差;y0为初始时刻频率偏差;a为频率漂移系数;xr(t)为随机项,也就是原子钟的噪声.可见,铯钟模型是一次多项式加随机项形式,氢钟模型是二次多项式加随机项形式.

1.2 原子钟噪声

氢钟和铯钟模型中,多项式部分是确定性部分,随机项部分是原子钟噪声的体现. 公认的原子钟噪声模型是以下五种噪声的线性叠加:频率随机游走噪声、频率闪烁噪声、频率白噪声、相位闪烁噪声、相位白噪声[16].

大量实验显示,对于典型的地面氢钟和铯钟(地面钟主要是和星载钟相区别),其主要的噪声为频率白噪声和频率随机游走噪声[17].

引起时差波动的主要是频率白噪声,引起频差波动的主要是频率随机游走噪声. 铯钟的频率白噪声相对较大,因而铯钟的短期时差波动较大,短期稳定度较差;氢钟的频率随机游走噪声相对较大,因而氢钟的频差波动较大,长期稳定度较差.

2 频漂估计算法

频漂是原子频标的确定性变化分量,很难对其进行直接测量. 一般先直接测量原子钟的相位或频率,然后通过下列方法估计频率漂移项[18-19].

2.1 现有的频漂估计方法(如表1所示)

表1 频漂估计方法

基于相位数据的频漂估计:

二次拟合:用二次多项式对相位差数据进行拟合,二次项系数乘以二得到频漂估计值.

二次差分均值:对相位差数据做二次差分取均值即可得到频漂估计值.

三点拟合:用相位数据的起点、中点和终点估计频漂,如式(3)所示:

D=4[x(end)-2x(mid)+

x(start)]/(Nt)2.

(3)

基于频率数据的频漂估计:

线性拟合:用一次多项式对频率数据进行拟合,一次项系数就是频漂估计值.

两段拟合:用频率数据的前一半均值和后一半数据均值计算频漂,如式(4)所示:

D=2[y(2ndhalf)-y(1sthalf)]/(Mt).

(4)

对数拟合:采用如下模型对频率数据进行拟合:

y(t)=a·ln(bt+1).

(5)

式中:a,b是拟合系数. 根据式(5),频率漂移可表示为

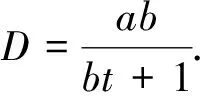
(6)

2.2 卡尔曼滤波方法

2.1节提到的是已有的估计频漂的算法,由于噪声的存在,导致上述频漂估计存在一定误差. 本文提出利用卡尔曼滤波算法对原子钟噪声建模,估计原子钟的频漂,能够在噪声存在的情况下更准确地估计频漂.

单台原子钟的卡尔曼滤波模型[20-25]:设x1(t),x2(t)和x3(t)分别是原子钟的三个状态:相位、频率和频漂,x(t)是相位x1(t)的测量值. 单台原子钟的模型为

x(t)=x1(t)+n1(t),

(7)

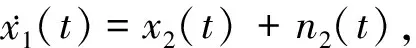
(8)

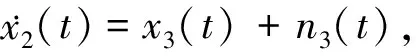
(9)

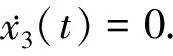
(10)

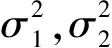
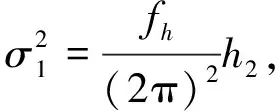
(11)

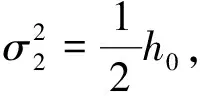
(12)

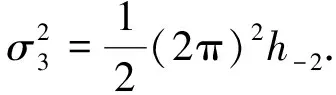
(13)

单台原子钟的模型的离散形式为

(14)

x(k)=x1(k)+n1(k).

(15)

式中:

w3(kτ)]dt,

(16)

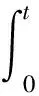
(17)

(18)

驱动噪声协方差矩阵Q和测量噪声协方差阵R分别是:

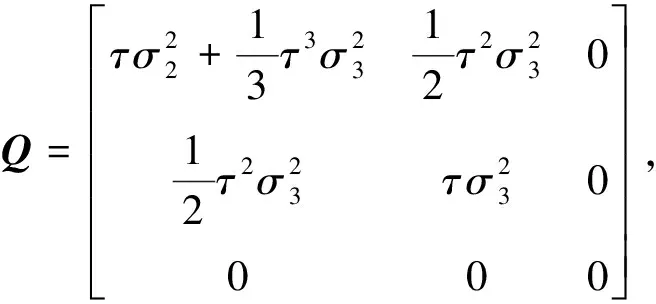
(19)

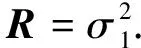
(20)

根据以上单台钟的卡尔曼滤波模型,估计Q矩阵和R矩阵,并且对状态矢量和滤波误差协方差矩阵赋初值,然后迭代计算就可以估计出原子钟的频漂.

3 两级卡尔曼滤波算法

本文提出两级卡尔曼滤波算法计算原子时:第一级卡尔曼滤波用于估计氢钟频漂并且对氢钟频漂校准,模型及参数估计如2.2节所述;第二级卡尔曼滤波用于生成原子时. 算法流程如图1所示.

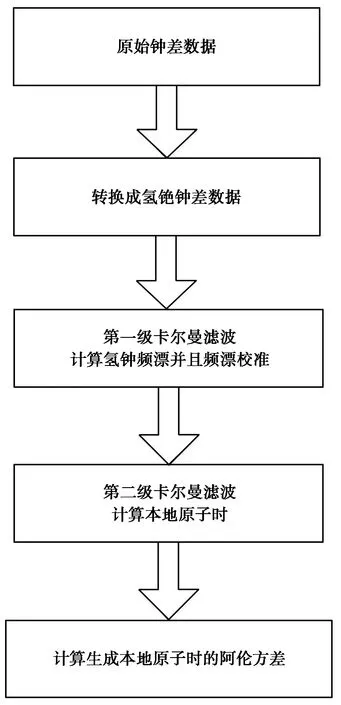
图1 两级卡尔曼滤波算法流程图

第二级卡尔曼滤波算法采用文献[17]提出的单状态变量卡尔曼滤波,即每台钟只有钟差一个状态变量.

钟组的状态方程表示为

Xk+1=Φk·Xk+uk.

(21)

式中:Xk=[x1(k),x2(k),…,xN(k)]T是钟组在k时刻的钟差;xi(k)(i=1,2,…,N)是钟组中第i台钟的钟差;Φk=IN×N是状态转移矩阵;uk是钟组的过程噪声,第i台钟的过程噪声方差表示为

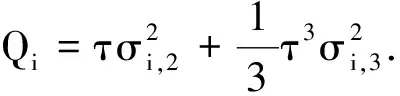
(22)

钟组的过程噪声协方差矩阵表示为

(23)

钟组的观测方程表示为

Z(k)=H·X(k)+V(k).

(24)

式中:H表示为

(25)

式中，V是测量噪声,表示为Vk=[V1(k),V2(k),…,VN-1(k)]T，Vi(k)(i=1,2,…,N-1)是每一组钟差的观测噪声,它们之间相互独立. 测量噪声协方差矩阵表示为

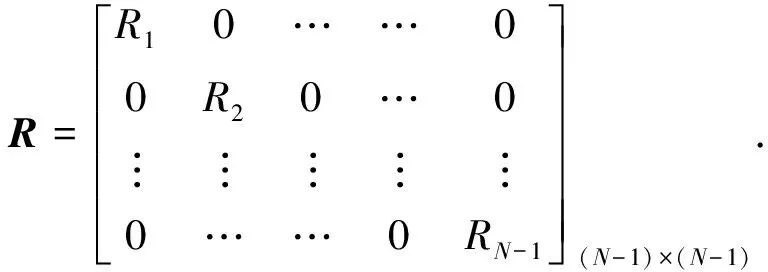
(26)

根据上述单状态变量卡尔曼滤波模型和噪声协方差矩阵,给定初始状态,按照卡尔曼滤波迭代计算就可以计算出每台钟的状态,即每台钟和综合原子时的钟差,用每台钟的钟差减去卡尔曼滤波结果就得到本地原子时.

4 实验结果

4.1 仿真实验条件

若采用实测数据,氢钟的实际频漂未知. 为了验证本文提出的卡尔曼滤波算法估计氢钟频漂的准确性,本文使用仿真数据,通过人为给氢钟加入频漂的方式,使氢钟的频漂变成已知量.

本文采用如式(1)、(2)所示的原子钟模型,使用文献[26]中所描述的方法,仿真生成2台氢钟和1台铯钟的数据. 仿真数据间隔1000 s,仿真生成86 400个数据点. 氢钟和铯钟的平方扩散系数σ2按照典型氢钟和铯钟的指标选取,如表2所示. 原子钟确定性部分参数配置如表3所示. 为了方便分析,设置观测噪声为零.

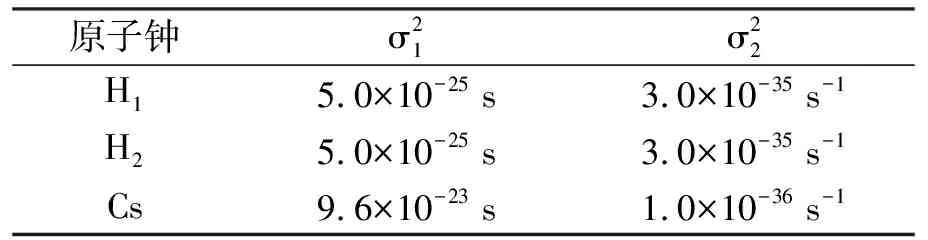
表2 随机部分参数配置

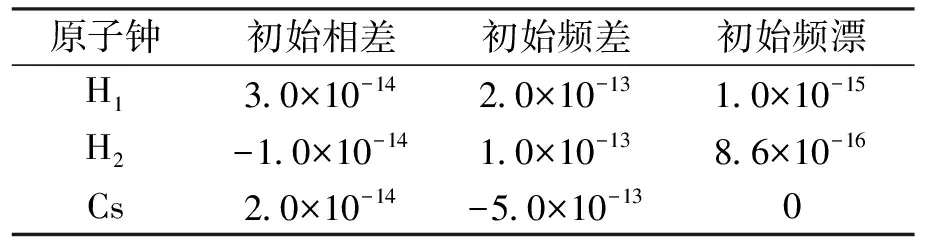
表3 确定性部分参数配置

4.2 频漂校准

将生成的氢钟和铯钟数据转换成氢钟相对铯钟数据的相位差. 由于典型地面守时型氢钟和铯钟的主要噪声是频率白噪声和频率随机游走噪声,所以在已有的估计频漂的方法中选用三点拟合法计算频漂,用于和本文提出的卡尔曼滤波算法估计氢钟的频漂作对比分析. 频漂计算结果如表4所示.

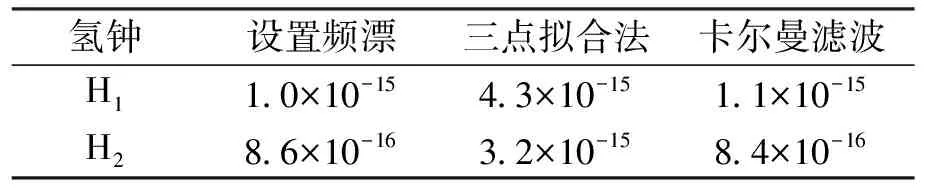
表4 频漂真值和频漂估计结果对比(天漂)

由表4可见,由于噪声的存在,三点拟合法估计的氢钟的频漂存在一定误差. 而本文提出的卡尔曼滤波算法通过对噪声建模,减小了噪声的影响,估计出的氢钟的频漂相对三点拟合法更接近氢钟真实的频漂. 表明本文提出的卡尔曼滤波方法估计氢钟的频漂更准确.

通过本文提出的卡尔曼滤波算法估计得到氢钟频漂后,再通过从钟差数据中减去二次项的方法对氢钟频漂校准.

4.3 原子时计算结果性能对比

将原始钟差数据分别用本文提出的两级卡尔曼滤波算法和经典的ALGOS算法以及AT1算法计算得到原子时,结果如图2所示.

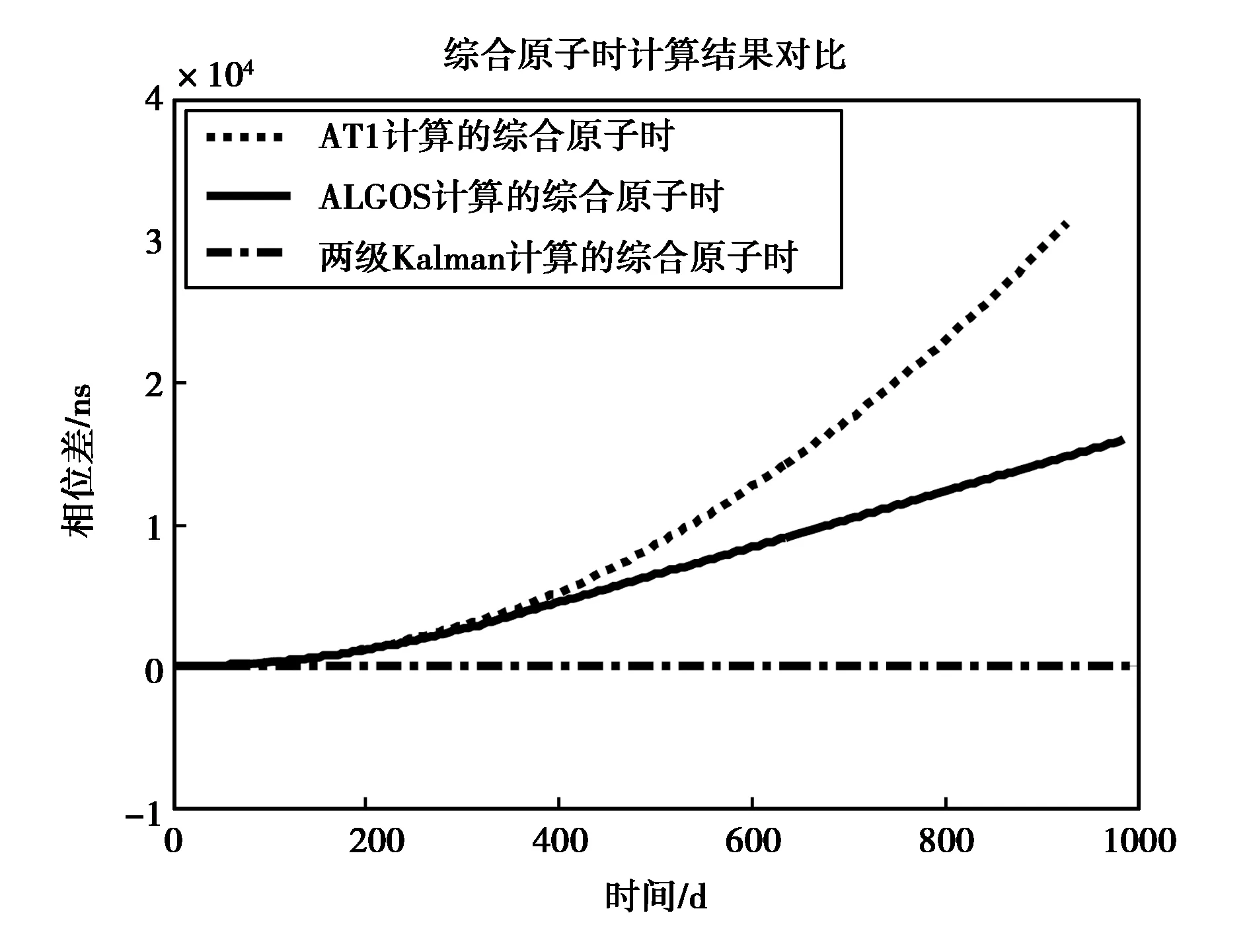
图2 综合原子时计算结果对比

由图2可以看到,ALGOS算法和AT1算法计算的原子时存在明显频漂,这说明氢钟的频漂反映在了生成的原子时中. 而用本文提出的两级卡尔曼滤波算法处理数据,经过对氢钟频漂校准后,计算的原子时几乎不存在频漂.

通过计算生成的原子时的阿伦方差,衡量生成的原子时的稳定度性能,阿伦方差计算结果如表5所示.

表5 原子时稳定度计算结果

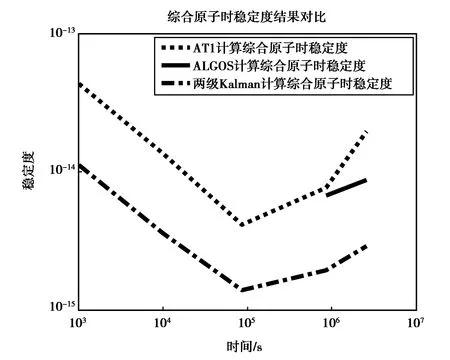
图3 综合原子时稳定度对比

根据表5和图3的结果可以发现,本文提出的两级卡尔曼滤波算法计算的原子时相对AT1和ALGOS算法计算的原子时的稳定度在千秒稳、万秒稳、天稳、十天稳和月稳性能都有提升,特别对于长稳,十天稳的提升在10-15量级,月稳的提升在10-14量级. 表明本文提出的两级卡尔曼滤波算法在对氢钟频漂校准后,生成的原子时在保持短期稳定度性能的基础上,长期稳定度性能得到了提升.

5 结 论

本文提出的两级卡尔曼滤波算法,通过对氢钟频漂校准,计算得到的本地原子时长期稳定度得到提升. 说明在计算本地原子时的时候需要考虑氢钟频漂,同时表明本文提出的两级卡尔曼滤波算法使铯钟的长期稳定度性能得到更有效的发挥. 这对于自主守时情况下,保持本地原子时的长期稳定有一定意义.

为了衡量频漂校准算法计算出的氢钟频漂的准确性,需要知道氢钟真实的频漂,而实测数据中氢钟频漂未知,因而本文使用了仿真数据.仿真数据相对实测数据的差异主要是:仿真数据只考虑原子钟主要的两种噪声:频率白噪声和频率随机游走噪声,不考虑测量噪声.而实测数据中,除了原子钟这两种主要噪声,还存在其他噪声,以及测量噪声.针对实测数据如何建模处理是进一步的研究工作.