脉动流下棒束通道内相位差及瞬态流场研究

2019-08-29祁沛垚谭思超郝思佳米争鹏

原子能科学技术 2019年8期

李兴，祁沛垚，谭思超,*，郝思佳，米争鹏

(1.哈尔滨工程大学核安全与仿真技术国防重点学科实验室，黑龙江哈尔滨 150001；2.中国核动力研究设计院，四川成都 610041)

LOCA条件或海洋环境影响下的反应堆处于流量非稳态工况，促使堆芯燃料组件的热工水力行为复杂多变，对燃料组件设计安全阈值提出了更高要求[1-2]。因此，非稳态条件下燃料组件内瞬态热工水力行为对于堆芯安全至关重要。脉动流作为一种非稳态的流动现象，在工程实际中经常出现，如事故条件下核电站主泵惰转或地震引起的流量波动、海洋条件下船舶装置内冷却剂流量的周期性脉动等，因此本文以脉动流这一非稳态工况作为棒束通道流量瞬态条件开展棒束通道内流动特性研究。

国内外学者针对圆管、窄通道内脉动流条件下瞬态特性已开展了相关研究。Ohmi等[3]针对脉动流条件下圆管内阻力特性开展了大量研究，分析了脉动频率、幅值等因素对阻力压降的影响。Gundogdu等[4-5]对圆管脉动流进行了理论建模，分析了层流、过渡流以及湍流状态下圆管脉动流阻力的主要来源。刘宇生等[6-7]对脉动条件下矩形通道内的压降和流量相位差进行了实验研究，分析了脉动周期、脉动振幅、通道结构尺寸和流体性质等因素对相位差的影响。张川[8]、Zhuang等[9]针对窄矩形通道脉动流阻力特性开展了大量实验研究。综上所述，目前针对圆管、窄通道等简单通道开展的脉动流条件下的相关研究较多，但对于复杂结构的棒束通道尚缺乏相关瞬态特性的研究，因此有必要针对脉动流条件下棒束通道内瞬态行为开展相关研究。

本文以脉动流为非稳态条件，开展棒束通道内脉动流相位差特性研究，分析脉动幅值、周期、主流流动状态对棒束通道相位差的影响。应用粒子图像测速(PIV)技术针对棒束通道内脉动流下的瞬态流场进行测量，分析脉动流不同阶段下棒束通道内各子通道内速度分布特征，并与稳态条件下子通道内速度分布进行对比。

1 实验装置

棒束通道实验系统(图1)主要包括流动回路、可视化实验段、光学系统、数据采集系统以及相关仪表设备。可视化本体以及光学系统固定于减震平台以尽量降低由振动引入的测量误差。实验装置详细介绍见文献[10]。

1.1 实验回路

实验在常温常压下进行，实验回路由循环水箱、离心泵、过滤器、测温传感器、电磁流量计、压力表、5×5棒束实验本体(燃料组件模拟体)以及相应的连接管道阀门等组成。实验回路水温由加热器和换热器共同调节，使实验回路内水温控制在(25.0±0.4) ℃。实验回路内脉动流量主要依靠计算机输出正弦电压信号到变频器，变频器接收信号后控制离心泵的转速来实现对棒束通道内流量的控制。实验本体上方布置压差变送器用来采集棒束通道内的压降。实验回路中电磁流量计的响应时间较快，因此忽略流量计的延迟时间。压差变送器的延迟时间为0.09 s。

1.2 实验本体

棒束通道实验本体由可视化棒束结构和可视化流道筒体组成，如图2所示。流动筒体由高度透明的有机玻璃粘结而成，通过法兰与上下腔室连接。棒束结构由25根氟化乙烯丙烯共聚物(FEP)材料的透明圆管组成，在流道筒体内呈正方形矩阵排列，FEP材料的折射率与水相近(折射率匹配误差为0.375%)，实验过程中可有效减低光路畸变误差。在棒束壁面上设置有引压孔，为排除入口及出口效应对棒束通道压降测量的影响，第1个引压孔布置在距离入口300 mm处，第2个引压孔设置在距离出口250 mm处，两引压孔间隔450 mm，具体布置如图2所示。

图1 试验回路系统Fig.1 Flow system

图2 棒束通道Fig.2 Rod bundle

1.3 实验误差

棒束通道压降测量采用压差变送器，测量误差为±1.5 Pa，响应时间为0.09 s。流量测量的不确定度为0.37%，响应时间忽略。采集系统采集的压降和流量数据均为电流信号，为采集同步，不存在延迟时间，故忽略采集系统的采集时间。棒束通道内瞬态流场采用PIV技术进行测量，棒束通道内速度的不确定度根据日本可视化协会的计算方法计算，计算的最大误差为5.7%[11]。

2 数据处理

图3 棒束通道内压降和流量间的延迟时间Fig.3 Response time between pressure drop and flow rate in rod bundle

棒束通道内压降Δp和流量G之间存在明显的相位差，如图3所示。为确定棒束通道内脉动流相位差，首先需计算压差变送器采集的压降数据和流量计采集的流量数据之间的延迟时间。为直观统计两者之间的延迟时间，采用压降和流量数据两波峰之间的时间差Δt减去压差变送器和电磁流量计的响应时间差，以获得棒束通道内压降和流量的实际延迟时间，最后根据每个工况的周期和延迟时间计算相位差。

流场测量过程中，脉动流速控制在300～650 mm/s之间，脉动周期为10 s，拍摄速度为4 000帧/s，且每100张图像(时间间隔为0.012 5 s)进行时均处理作为1组瞬态数据。根据棒束通道结构的对称性，为提高棒束通道流场分辨率，以棒束通道的中轴线为分界线，集中高速摄影仪的1 024×1 024像素于棒束通道内一半实际区域27.75 mm×27.75 mm，如图4所示。PIV分辨率为0.032 mm/pixel。PIV后处理程序为LaVision公司的二维PIV处理软件Davis，后处理计算中的过程参数介绍详见文献[10]。

图4 PIV测量位置Fig.4 PIV measurement position

3 流场结果及分析

3.1 实验工况

实验在常温常压下进行，棒束通道脉动流相位差实验工况覆盖了层流、过渡流和紊流，平均雷诺数为800、2 500、9 000，振幅为0.2、0.4、0.6，周期为20、30、50、100 s。针对脉动流条件下棒束通道内流场研究，开展了脉动周期为10 s、平均雷诺数为4 000、振幅为0.6的流场测量。

3.2 光棒通道脉动流相位差

根据文献[12-13]对圆管脉动流流场的研究，对相位差的产生可做如下分析：当驱动压力周期作用于流体时，通道壁面边界层内随之产生剪切波，剪切波从壁面开始向主流中心传播，且在此过程中逐渐衰减[14]，黏性剪切波传递距离与管道尺寸之间的关系为相位差产生的主要原因。综上所述，棒束通道内的脉动流相位差主要来源于流体在径向上惯性力与黏滞力之间作用的关系，管道内压力传递较快，忽略压力的传递时间，因此相位差主要来源为流体的提速过程。

图5为光棒通道内脉动流在不同平均雷诺数Reave(800、2 500、9 000)和不同振幅Ar(0.2、0.4、0.6)下的相位差随周期的变化趋势。

图5 光棒通道内相位差Fig.5 Phase difference in bare rod bundle

从图5可发现：1) 棒束通道内相位差随脉动周期的增加逐渐降低，分析主要原因为随周期的增长，棒束通道内的延迟时间变化较小，因此随周期的增加，相位差不断减小；2) 棒束通道内的相位差几乎独立于脉动振幅，即棒束通道内相位差不随振幅而变化，分析主要原因为脉动振幅并没有影响径向上的能量传递过程，因此并未对棒束通道内的相位差产生明显的影响；3) 棒束通道的相位差随主流平均雷诺数的增加逐渐降低，即不同流动状态下延迟时间存在明显的区别，随流速的增加整体延迟时间变短，主要原因为随平均雷诺数的增加，棒束通道内流体的随机运动能力增强，逐渐向湍流过渡，进而促进棒束通道径向的动量传递，因此棒束通道内相位差变短。

3.3 带定位格架棒束通道内相位差

为分析定位格架在棒束通道内对相位差的影响，在光棒通道中加入了带搅浑翼的定位格架，该格架对流体在径向上具有较强的交混能力。定位格架布置在距第1个引压孔200 mm处，开展与光棒通道实验工况相同工况的实验，脉动流的相位差如图6所示。从图6发现，在各种流动状态下棒束通道内相位差明显缩短，且流态之间的差异也明显缩小。分析原因为定位格架对棒束通道内流场产生横向扰动，破坏了棒束壁面附近的边界层，从而促进了棒束通道内在径向上的能量传递，提升了壁面附近流体对压力的响应能力，缩短了压降和流量之间的延迟时间，进而降低了相位差。

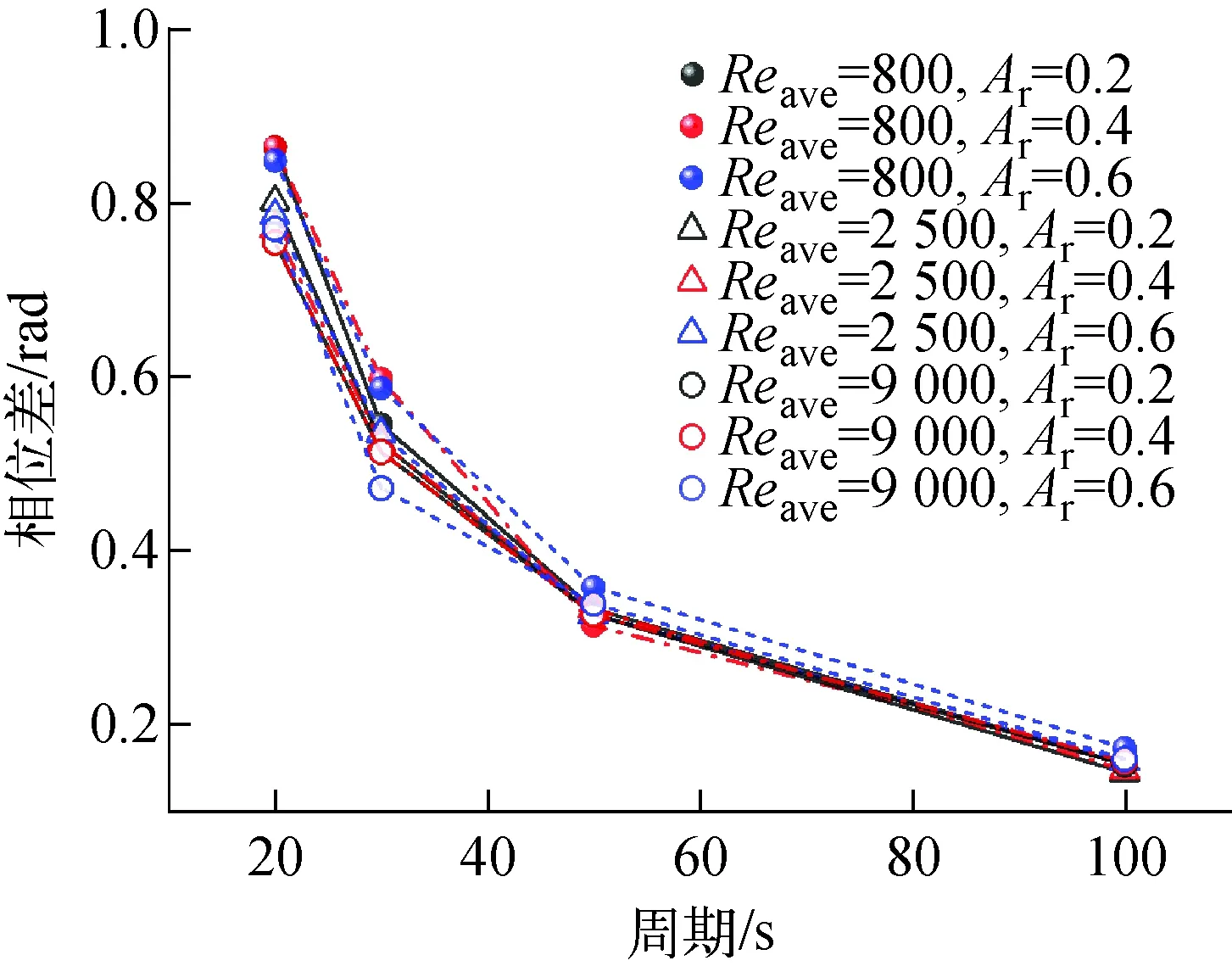
图6 带定位格架棒束通道内相位差Fig.6 Phase difference in rod bundle with spacer grid

3.4 棒束通道内流场分布特性

为直观展示脉动流条件下棒束通道内的流场分布，采用PIV技术对棒束通道内流场进行了测量。为对比棒束通道内流场在稳态与瞬态条件下的差异，在流量波动范围内开展了3种稳态工况下的测量。稳态工况与瞬态工况的重合位置如图7中1、2、3、4和5所示，其中位置1和2具备不同负加速度(a<0)，位置3和4具备正加速度(a>0)，且位置1和4具备大小相同方向相反的加速度，位置2和3具备大小相同方向相反的加速度，位置5不存在加速度。

图8为稳态工况1与瞬态工况2、3对应的棒束通道内速度分布。结合图8a稳态条件下的速度分布，发现子通道4和子通道5内速度幅值几乎相同，各子通道内速度分布趋势基本呈抛物线状；另外，子通道6内速度幅值明显低于子通道4、5，主要原因为子通道6右侧为方形通道壁面，该壁面对流体的阻力作用明显大于棒束壁面，因此导致子通道6的速度幅值较低。图8b为瞬态工况2下对应棒束通道内速度分布，该工况下流体速度具备负加速度，与稳态工况相比，子通道内速度分布出现明显的差异，子通道4内速度幅值小于子通道5速度幅值，子通道6内的速度大于稳态条件下的速度。图8c为瞬态工况3下对应棒束通道内速度分布，该工况下流体具备正的加速度，但该工况下各子通道内速度分布与瞬态工况2的速度分布趋势基本相同，同样表现出子通道4内速度小于子通道5内速度，子通道6内的速度大于稳态条件下的速度，棒束通道内在瞬态和稳态工况下展现的差异主要是因为棒束通道的流体具备一定的加速度导致的，但棒束通道内速度分布对于加速度响应特性与圆管脉动流速度分布的“环状效应”[14]出现明显区别，主要原因为棒束通道内壁面较多，对流体黏滞阻力作用明显，导致流体对一定范围加速度变化的响应不明显。在瞬态工况2和3下流体虽具备不同的加速度，但加速度幅值较小，对棒束通道内全流场的作用十分有限，因此子通道4和5的速度分布趋势并没有明显变化，但对单一子通道作用较明显，如在瞬态工况2和3下子通道4内速度分布存在明显差异，瞬态工况2下的子通道4内速度分布出现明显的“平顶”。

图7 稳态流量和脉动流量Fig.7 Flow rate under steady state and unsteady state

a——稳态工况1(a=0)；b——瞬态工况2(a<0)；c——瞬态工况3(a>0)图8 稳态工况1与瞬态工况2、3下的速度分布Fig.8 Velocity distribution under steady condition 1 and transient condition 2 and 3

图9为稳态工况2与瞬态工况1、4对应的棒束通道内速度分布。与瞬态工况2、3相比，瞬态工况1、4具备较大的加速度，因此瞬态条件下速度分布展示出明显的差异。稳态工况2下棒束通道内流速分布与稳态工况1除各子通道速度幅值不同，子通道内速度分布趋势并无明显差异。结合图9b发现瞬态工况1与瞬态工况2子通道内速度分布趋势基本相同，即子通道4内的速度低于子通道5内的速度，由于棒束通道结构的对称性，整个棒束通道内在该条件下的速度分布呈“凹”形状，即棒束通道边缘的子通道内速度较高，中心子通道速度较低。结合图9c发现棒束通道瞬态工况4与瞬态工况3子通道内速度分布明显不同，瞬态工况4条件下流体具备较大的正加速度，展现出速度分布特性为子通道4内速度大于子通道5内的速度，考虑到棒束通道的对称性，整个棒束通道内在该条件下的速度分布呈“凸”形状，即棒束通道内中心子通道速度大于边缘子通道。因此，在瞬态条件1与4下棒束通道内整体子通道之间的速度分布与圆管内往复速度的“环状效应”较相似。

图10为稳态工况3和瞬态工况5对应的子通道内速度分布，稳态工况下各子通道内速度分布与其他稳态条件下的速度分布趋势基本相同。瞬态工况5下不具备加速度，子通道4内速度幅值略高于子通道5。结合以上瞬态工况发现，即使棒束通道内流体主流加速度变为0，但子通道内的速度分布由于流体的黏滞效应并未立刻停止变化，仍在一定时间内表现为正加速度的速度分布特征，该现象与瞬态工况3的延迟效应基本一致。

a——稳态工况2(a=0)；b——瞬态工况1(a<0)；c——瞬态工况4(a>0)图9 稳态工况2与瞬态工况1、4下的速度分布Fig.9 Velocity distribution under steady condition 2 and transient condition 1 and 4

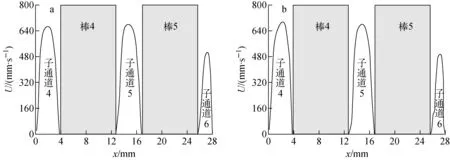
a——稳态工况3(a=0)；b——瞬态工况5(a=0)图10 稳态工况3与瞬态工况5下的速度分布Fig.10 Velocity distribution under steady condition 3 and transient condition 5

综上所述，棒束通道内瞬态流场演化大致过程为：在瞬态工况1向瞬态工况2过渡过程中，由于负加速度不断减小，棒束通道流场分布的“凹”型逐渐减小。在瞬态工况2向瞬态工况3过渡过程中，负加速度变成正加速度，但子通道4和子通道5在两个瞬态工况下展示出的差异较小，其主要原因有两点：1) 瞬态工况2和瞬态工况3具备的加速度幅值较小，对流场的作用较弱；2) 瞬态工况2向瞬态工况3过渡中棒束通道内流动状态基本处于层流阶段，径向能量传递能力较弱，导致子通道4和子通道5之间的能量传递较弱，维持了子通道原有速度分布特征。实际上，在瞬态工况3和瞬态工况4之间的某个工况下子通道4和子通道5存在相同的速度幅值，越过该位置后棒束通道内整体流场分布才展现出“凸”型，即子通道4和子通道5速度相同对应瞬态工况不出现脉动流波谷，而是出现在波谷之后的位置。在瞬态工况4向瞬态工况5过渡过程中，棒束通道内流体的正加速度逐渐减小，并伴随着棒束通道内的流动状态向湍流状态转变，横向上的能量传递能力不断增强，进而导致两个子通道内的速度差异变小。以上现象说明：脉动流条件下棒束通道内流场会出现类似于圆管脉动流“环状效应”，但由于棒束通道复杂的几何结构和不均匀的速度分布导致整体棒束通道内“环状效应”滞后于主流量变化。