船舶充液管路振动响应计算与试验*

吴江海， 尹志勇， 孙凌寒， 孙玉东

(中国船舶科学研究中心船舶振动噪声重点实验室 无锡，214082)

引 言

舰船管路系统由机械设备(主要是各类泵和风机等)、管道、支撑结构、弹性接管和各类阀件等组成。机械设备振动与水动力噪声沿管壁与管内流体介质传播到船体及舷外形成水下辐射噪声。管路系统产生的水下噪声与机械设备的源特性、管路结构与流体介质的声传播特性、管路支撑结构、船体的机械阻抗特性及通海口的辐射阻抗特性都有关系，几乎涉及到舰船声隐身研究的各个方面。

学者们在研究管路振动时采用了各种计算方法，主要包括：特征线法(method of characteristics,简称MOC)、有限元法(finite element method,简称FEM)和传递矩阵法(transfer matrix method,简称TMM)。这些方法有各自的优缺点与适用条件，也可以互相结合产生新的混合方法(Hybrid Method)，特征线-有限元法(MOC-FEM)就是其中之一。特征线法是文献中较早用来计算管道振动的数值方法，主要通过把偏微分方程转为常微分方程，然后在距离-时间平面内沿特征线进行积分，主要用于在时域内计算压力波和轴向应力波的传播。Wiggert等[1]对充液管系振动的“十四方程”模型的特征线方法进行了阐述。许多学者将有限元用于求解流体方程、结构方程或者对整个模型进行运用。Lavooij等[2]最先将有限元法与特征线法结合起来分析系统的响应。Heinsbroek[3]分别用MOC-MOC法和MOC-FEM法计算了非刚性支撑的管路系统的响应，并比较了这两种方法的优劣。De Jong[4]研究了管路系统的振动与声响应预报的传递矩阵法，考虑了水泵的噪声源特性并研究了实验室的测试方法，但该方法没有明确测试数据域预报方法之间的相关性。此外，传递矩阵法在处理一定规模、多分支的管路系统也存在困难[5]。笔者提出一种基于理论计算与试验测试相结合的管系振动计算方法，并进行相关的试验验证。

1 理论计算方法

阻抗综合法的基本思想是将一个复杂系统分割为若干子系统，各子系统之间以节点相互连接。节点代表了子系统间的一个或多个相互作用点。划分子系统的基本原则是划分的子系统尽量少且便于获取各子系统的阻抗矩阵[6-8]。将管路系统划分为多个子系统后，运用理论或试验的方法获得各子系统包含所有连接点所有自由度的阻抗矩阵，根据子系统连接点的约束条件，获得整个系统的阻抗矩阵。这种方法与动态子结构法有相似之处，其最大优点是对一些难于进行理论分析的子系统可以采用阻抗试验数据，便于工程应用。

1.1 直 管

假定轴向波、横向波和扭转波在沿直管传递时互不影响。由于流体介质的存在，轴向振动包含了沿流体介质传递的平面波及沿管壁传递的纵波，二者在振动传递过程中会由于管壁的弹性而相互转换。如图1所示，一段充满流体介质、管壁材料均匀的直管其轴向传递的纵波与管内平面波通过管壁材料的弹性作用相互耦合的运动方程[9]为

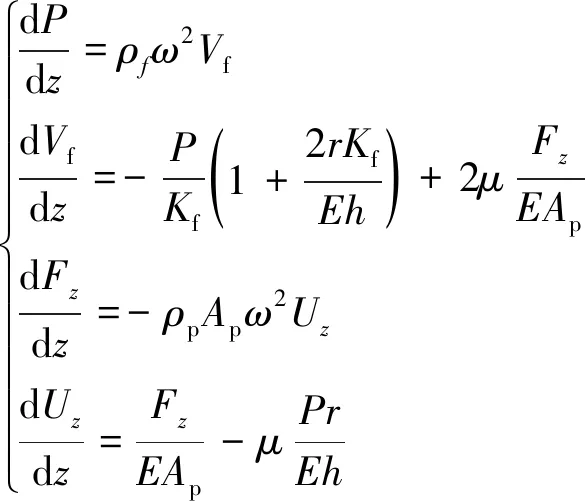
(1)

图1 直管单元示意图Fig.1 Straight pipe element

式(1)考虑了管壁弹性材料的泊松比对管内声速与声压的影响。管道的横向振动用Timshenko梁建模，管内流体在横向对管壁仅考虑其附加质量作用，不考虑管壁的横向运动对流体的影响。这种简化在管道的截止频率范围内有足够的精度。直角坐标系下，管道在两个垂直的横向振动方程[10-11]为

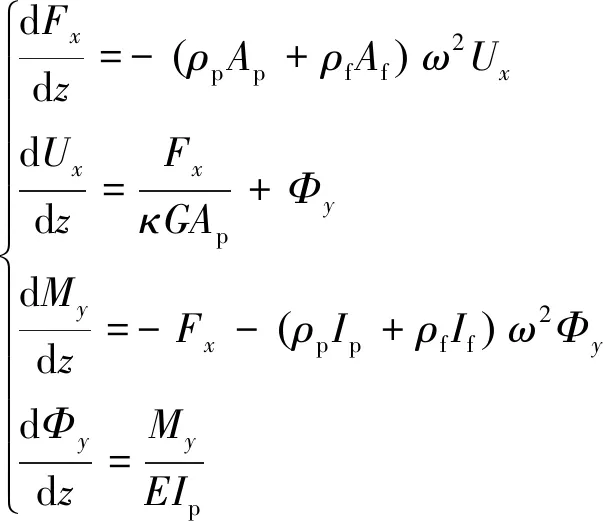
(2)

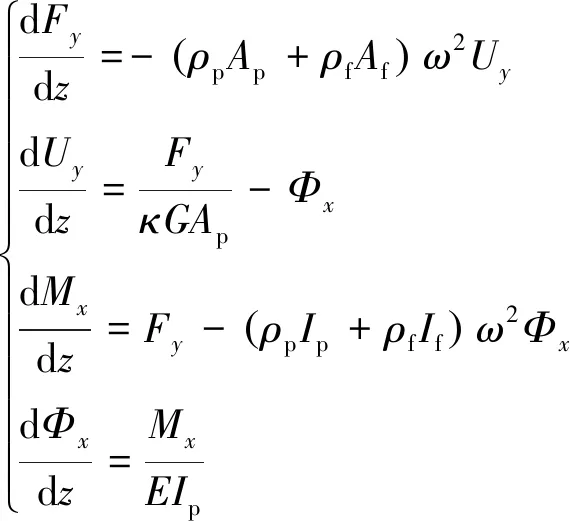
(3)

直管的横向振动是弯曲与剪切的耦合振动。一般长径比较大的管道其横向振动以弯曲波为主，反之以剪切波为主。直管的扭转振动是一个独立的运动，只传递扭转波。由于忽略流体的黏性，管壁的扭转振动不引起流体的运动，因此充液直管的扭转振动方程与空的直管或一般杆的扭转振动方程一致，表达式为

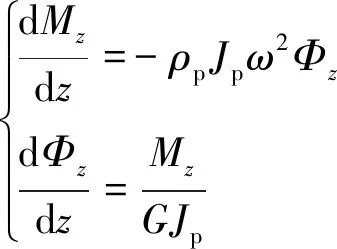
(4)

式(1)～(4)构成了充液弹性直管流固耦合振动的“十四方程”模型。

假定直管流固耦合振动微分方程的解为

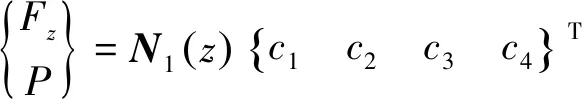
(5)

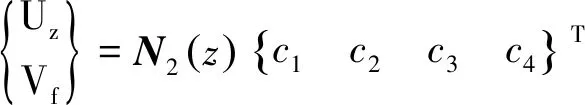
(6)

令z=0,l，得到管道两端力与位移的表达式，消去4个未知系数，得到直管的轴向阻抗矩阵为

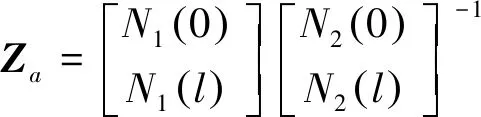
(7)

直管横向及扭转阻抗矩阵可以用同样的方法得到。直管轴向与横向阻抗矩阵均为4阶，扭转矩阵为2阶。将这些矩阵按一定顺序组合，得到直管的14阶总阻抗矩阵。

1.2 弯 管

弯管相对直管比较复杂。截面的弯管其弯曲刚度相比圆截面管偏低。这一方面是由弯管结构本身引起的，另一方面实际弯管截面通常为椭圆形，也是降低其弯曲刚度的原因之一。在弯管的弯曲振动模型中引入一个挠性因子。挠性因子为同样截面的直管弯曲刚度与弯管弯曲刚度的比值，与弯管的弯曲半径、相邻结构和截面的椭圆率有关。文献[4]给出了用曲梁的理论模型并引入挠性因子获得的弯管振动微分方程：该方程组中令R→∞，并令挠性因子ft=1，得到直管的“十四方程”。应用该方程难以获得阻抗矩阵的理论表达式，只能应用数值方法求解。

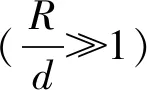
(8)

图2 弯管单元离散示意图Fig.2 Discrete model for curved pipe

应用阻抗矩阵与传递矩阵元素之间的关系获得弯管阻抗矩阵为

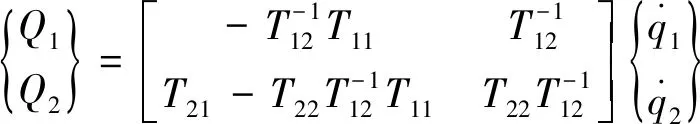
(9)

1.3 边界条件

管路支撑或船体只传递结构振动，在节点部位具有位移连续条件、声压连续条件及节点力平衡条件

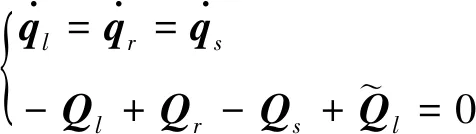
(10)

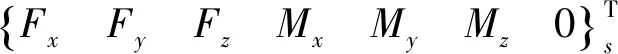
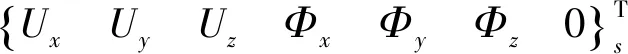
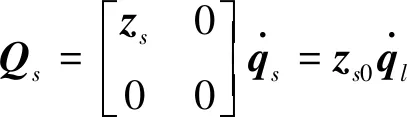
(11)

将节点力平衡条件用节点速度表示为

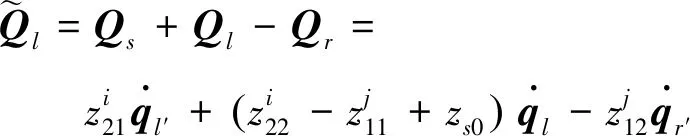
(12)

利用式(12)得到引入支撑或船体结构边界阻抗后的节点阻抗矩阵为

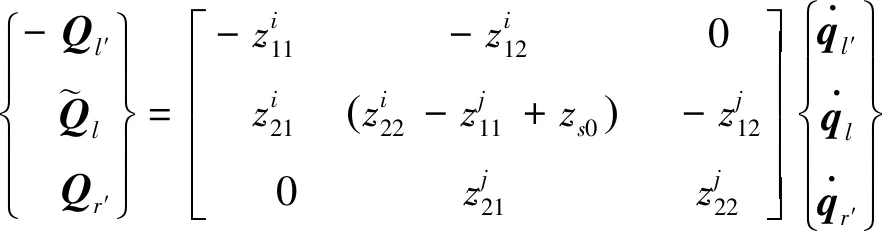
(13)

可见，支撑与船体结构边界条件的引入方法是在节点阻抗矩阵上直接叠加上边界输入阻抗。如果考虑支撑与船体结构在各节点间的耦合，还必须在总阻抗矩阵中组装节点间的传递阻抗，其方法与输入阻抗一样，直接在对应的行列上叠加传递阻抗。

1.4 振动响应计算

如图3所示，假设管路左端为激励端源i1，支撑上端为S1,下端为S2，管路末端为h。根据边界处阻抗相加的边界条件可以得到整个系统的传递阻抗矩阵为

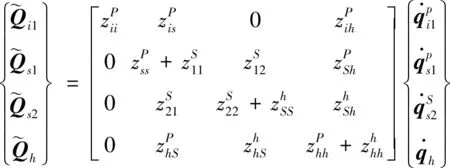
(14)

式(14)中左端为4个节点处的力，右端为各节点的振动响应速度。将直管(弯管)阻抗以及支撑、船体的阻抗代入式(14)，若已知激励力的大小，可得到管路与船体的振动响应。

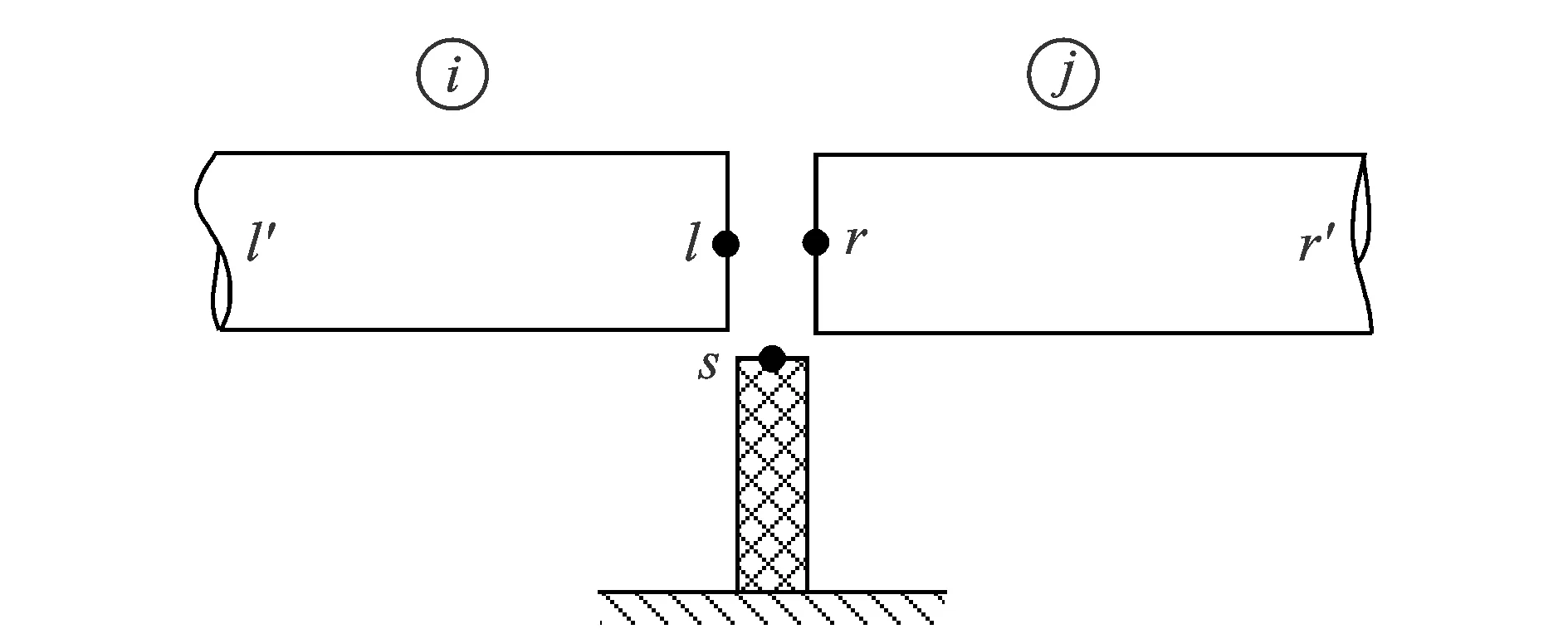
图3 支撑或船体边界节点Fig.3 Support and ship hull boundary

2 有限元仿真计算

2.1 直管路验证

该模型为四边固支平板上通过3个支撑连接的一段直管段。平板尺寸为6 m×6 m×0.02 m ，平板采用壳单元，网格尺寸为0.1 m，整个平板的质量为5 616 kg，网格数量为4 600，平板四边固支用以模拟刚性不动基础。

管路系统采用一段长为4 m的直管，规格为Φ50×8，每隔1 m共3个支撑连接在基础平板上。由于整个管路比较细长，故采用梁单元，管路的网格尺寸为0.01 m，整个管路的网格数量为400，质量为72.14 kg。管内水的质量通过附加质量均匀分布在管路梁单元上，质量为22.167 kg。在管路3/8与5/8处通过集中质量加载7.35 kg，用以模拟管路中法兰质量块。整个模型及直管编号如图4所示。

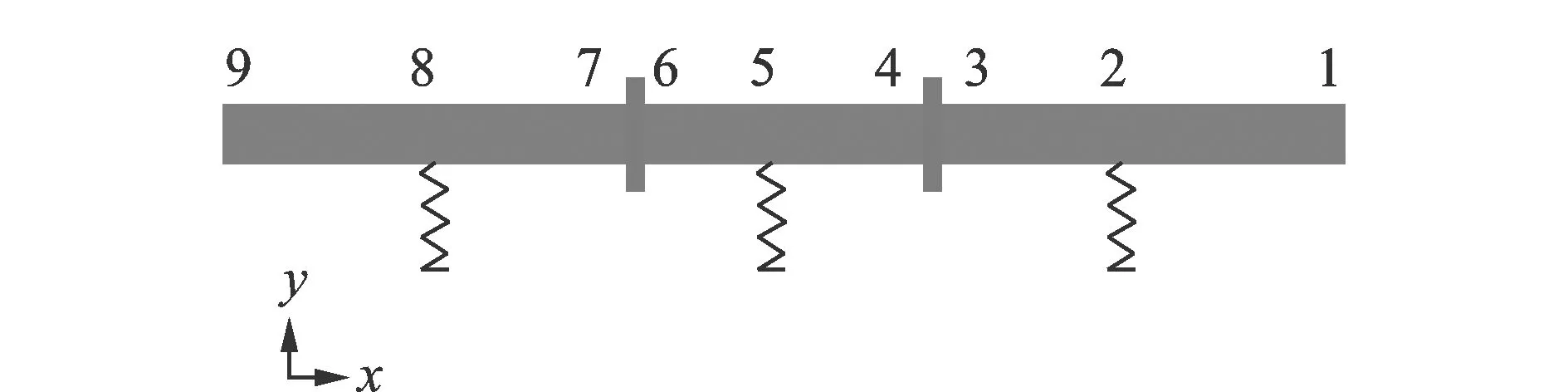
图4 直管模型Fig.4 Straight pipe model

算例中在管路末端加载垂向单位激励力，考察管壁上的测点与连接支撑下端点的振动响应。阻抗综合法是将管路系统离散为各个部件对其两端点进行编号，获取其空间坐标位置。

船体的阻抗值是阻抗综合法中重要的输入源数据，通常采用的办法有计算数值与试验测试两种。试验测试中，模型空间较为复杂、测点较多，建议采用锤击法获取船体阻抗。若安装环境允许，建议采用激振器进行激励测试船体阻抗，激振器的信号较为稳定，则船体阻抗获取较为准确。该计算办法获取船体阻抗的成本较低，因计算条件的限制，船体阻抗的频率范围决定振动计算的频率上限。本算例采用有限元对2，5，8这3个测点处的阻抗进行了计算。管路支撑是管路振动传递到基础的重要途径，这里计算两种管路支撑模型，包括单一的纯刚度k=1×106和采用实测弹性管路支撑(flexibility pipe support，简称FPS)系列管路橡胶弹性隔振器刚度。纯刚度采用弹簧单元进行模拟，橡胶弹性支撑采用三向动刚度进行模拟。

笔者采用阻抗综合法建模计算和有限元一体化建模两种计算方法对该管段模型进行振动传递响应计算分析。支撑弹簧刚度为1×106N/s，计算结果如图5所示。

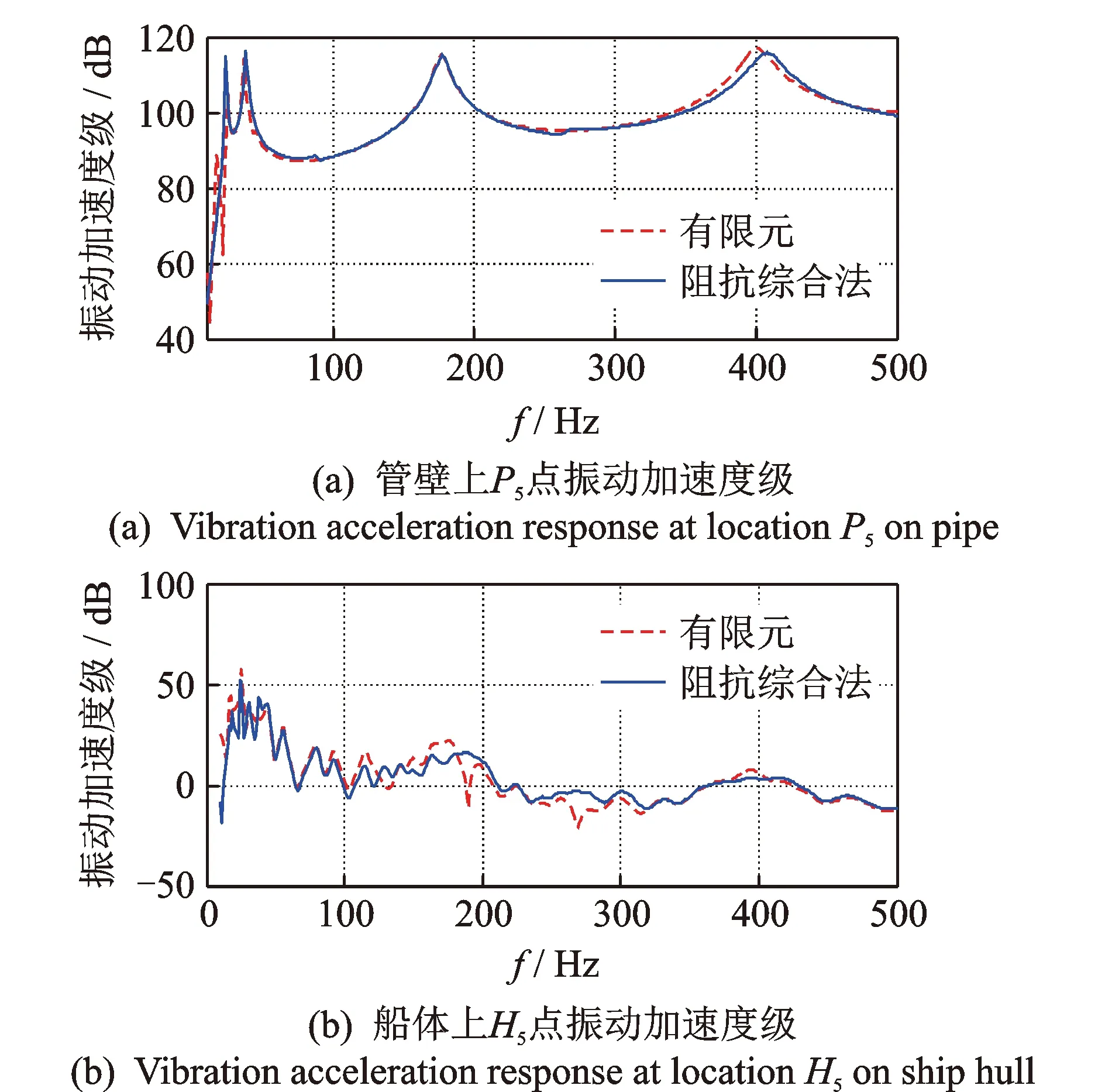
图5 k=1×106计算结果对比Fig.5 k=1×106 comparison of calculation results

从简单支撑管路计算结果来看，两种方法在管壁与支撑下端的振动响应吻合程度较好，其中管壁上吻合程度更好。这是因为阻抗综合法对该类直管采用了较为精确的公式进行计算，与有限元计算差异不大。对于管路支撑部位的模拟，有限元只是采用了三向刚度，阻抗综合法则采用的是隔振器上下端原点、传递3个方向共9列的阻抗数据，因此阻抗综合法计算可以更加真实地反应各振动方向之间的耦合。这种差异现象在采用复杂支撑时，两种计算方法的结果更加明显。

实测管路支撑阻抗数据计算结果对比如图6所示。两种支撑情况下振动加速度总级如表1所示。

图6 橡胶支撑计算结果对比Fig.6 Comparison of calculation results under rubber support

方法H5(弹簧)P5(弹簧)H5(橡胶)P5(橡胶)阻抗法56.61132.3857.97130.64有限元法59.19132.7958.01132.23

2.2 复杂管路验证

采用综合管路中T型管段进行计算方法验证，该T型管段包括直管、弯管和三通管等，形式复杂，能较好地反应舰船中真实的管路空间走势。管路系统由DN100和DN80两种管径组成，包含4各管路支撑和6片法兰。管路安装图与阻抗矩阵法模型如图7所示。

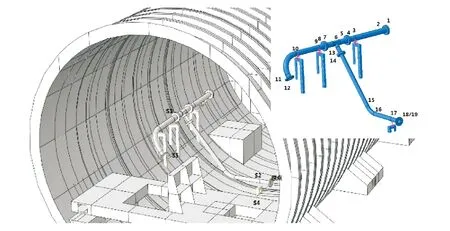
图7 典型T型管段Fig.7 Typical T-type pipeline system

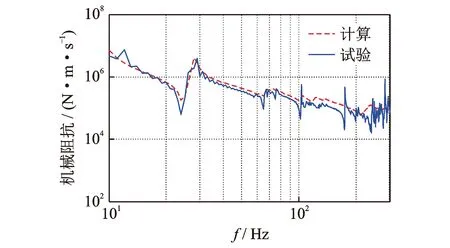
图8 船体阻抗计算结果对比Fig.8 Comparison of impedance

船体阻抗是阻抗矩阵计算方法中重要的输入数据，本算例中的阻抗采用有限元计算获取，同时对管路支撑处的船体阻抗进行了测试，以验证有限元模型的精度。图8为船体阻抗计算结果对比。从计算与试验测试阻抗对比图看，有限元计算阻抗值较为精确，是保证下一步阻抗矩阵法计算精度的重要前提。

图9为T型管段计算结果对比。从图9看出，采用有限元与阻抗综合法计算结果基本一致，说明本计算方法具有较好的精度。对于大型复杂空间管路，该方法只需通过有限元计算出支撑位置相应的船体阻抗，而无需建立空间管路复杂几何外形。

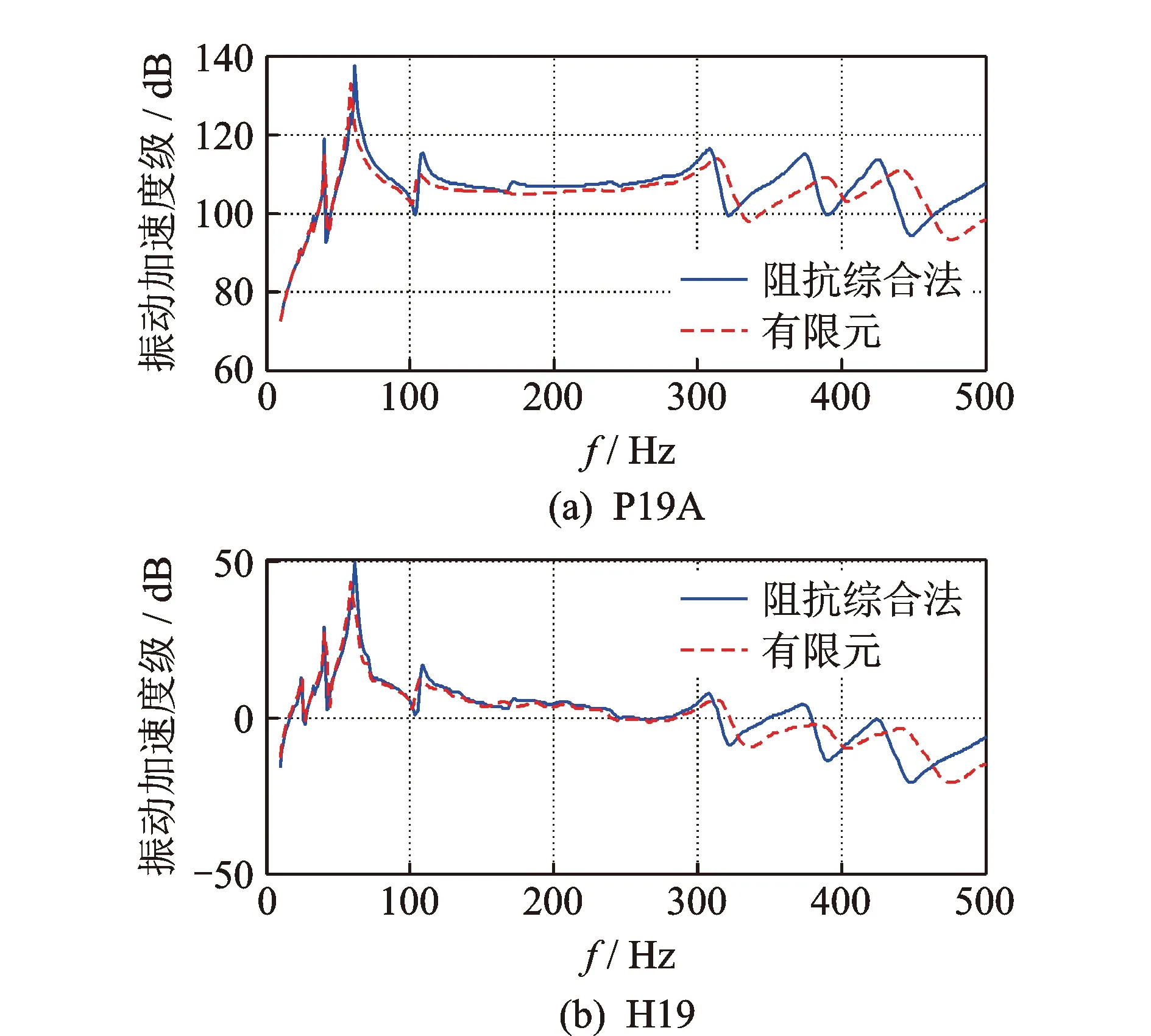
图9 T型管段计算结果对比Fig.9 Calculation results of T-type pipeline

3 试验结果对比

针对上节中的T型管段，开展相应的试验验证。为了测试船体阻抗具有较高的频率上限，采用激振器激励船体测试管路支撑位置处的船体阻抗，作为阻抗矩阵法中的输入源数据。船体阻抗测试需要同时获取该点处的力与振动响应，试验中在支撑位置粘贴加速度传感器获取振动响应，在激振器杆上安装力传感器获取激励力。

图10 阻抗测试激振器安装Fig.10 Exciter installation of impedance test

对管路系统中管壁与船体上的测点振动响应进行计算对比分析，结果如图11所示。对比分析显示，测试的振动总级为64.563 dB,而本研究的计算振动总级为64.2456 dB。可见，本研究的计算方法具有较好的精度，且计算频率范围高于传统的有限元计算。

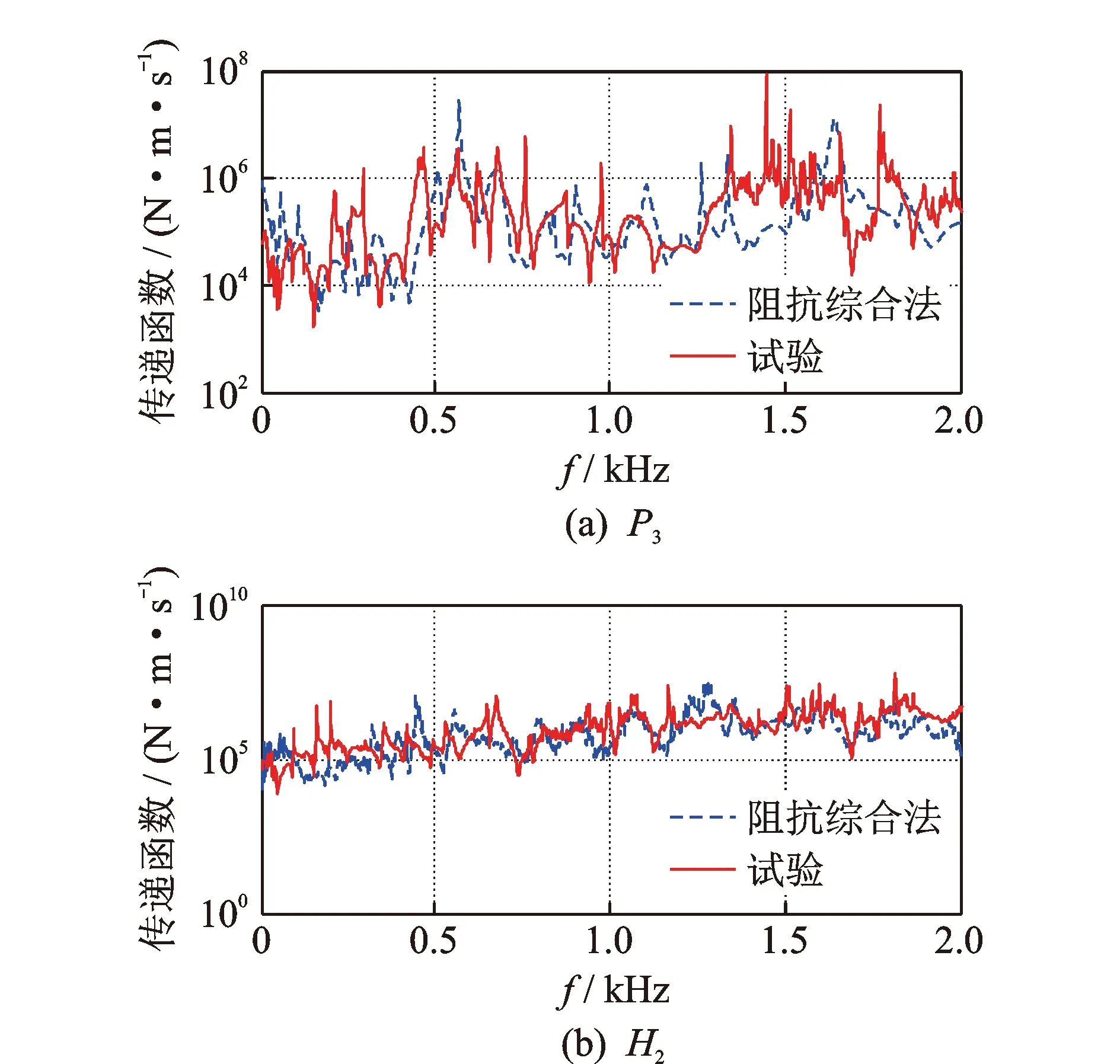
图11 动态响应对比Fig.11 Comparison of dynamic responses

4 结束语

笔者介绍了阻抗综合法管路计算方法，采用简单直管模型与船体T型管段对阻抗综合法计算进行了验证。计算结果表明，采用阻抗综合法与有限元一体化建模计算结果吻合程度较好，管路弹性支撑可以将实测阻抗数据转换成三向动刚度并代入有限元中进行计算。针对船体中T型管段，采用激振机获取船体管路支撑处阻抗，将阻抗代入阻抗综合法中。从管路一段传递到另一端的传递函数计算与试验结果表明，本研究的计算方法具有较高的精度与工程应用价值。