一种新的固有频率跟踪及虚假频率剔除方法*

周昊天， 赵 婕， 曹为政, 赵 锐， 于开平， 白云鹤

(1.哈尔滨工业大学航天学院 哈尔滨，150001) (2.黑龙江科技大学计算机与信息工程学院 哈尔滨，150022) (3.中国电子科技集团公司第54研究所 石家庄，050081)

引 言

结构模态参数辨识是结构动力学的重要研究内容，当前已经有众多成熟方法用于解决定常系统的非时变模态参数辨识问题，例如随机减量法[1]及随机子空间方法[2]等。由于线性时变系统比定常系统复杂，同时，适用于定常非时变系统的模态参数辨识方法并不能直接应用于线性时变系统，而时变系统在实际工程应用中又是普遍存在的，因此对线性时变系统的模态参数辨识一直是研究的热点。

在时变系统中，传统的模态参数的概念不复存在。Liu[3]提出了“伪模态参数”的概念，并将其推广用于线性时变系统[4]。目前，已有的用于时变模态参数辨识的方法包括基于时频分析的辨识方法[5]、基于盲源分离的辨识方法[6]和基于时间序列模型的方法[7]。对于工程实际而言，应用最为广泛的是基于子空间的辨识方法[8]。Liu等[9]提出一种基于子空间的时变模态参数辨识方法，并对一个移动质量梁的伪固有频率进行了识别。于开平等[10]提出一种利用系统输入输出整体数据进行时变模态参数辨识的方法，对一个移动简支梁的伪固有频率进行了辨识，并提出改进方法[11]。庞世伟等[12]引入投影估计子空间算法(projection approximation subspace tracking，简称PAST)，提出了采用固定长度平移窗的递推子空间辨识方法，利用该方法对移动质量简支梁进行了辨识。杨凯等[13]引入自然幂迭代算法(natural power iteration，简称NPI)和逼近幂迭代算法(approximated power iteration，简称API)，对移动分布质量-悬臂梁和两自由度弹簧-质量系统进行了时变模态参数辨识。倪智宇等[14]提出了一种用于时变模态参数辨识的截断窗逼近幂迭代子空间方法(truncated window approximated power iteration，简称TW-API)，并将该方法用于二连杆机械臂和在轨航天器[15]的伪固有频率辨识中。

由于子空间跟踪算法本身的限制和测量数据受噪声污染的影响，识别结果中通常混杂了虚假的模态信息[9]，因此提高最终识别结果的精度是一项重要的研究内容。除了采用精度更高的跟踪算法以外，另一种研究思路是对识别结果进行处理，采用特定的算法识别出真实模态、剔除虚假模态。Liu等[9]提出了一种针对慢变的伪固有频率筛选方法，该方法计算量小，但需要给出若干估计的频率值。Zhou等[16]引入fuzzy C-means方法，提出基于模糊聚类的模态参数验证方法，即通过欧氏距离检测不同阶次之间的差异，从而实现对伪固有频率的筛选。

为了提高最终结果的精度，笔者引入新信息准则子空间跟踪算法[17](novel information criterion，简称NIC)，针对时域类模态参数辨识方法常见的虚假频率问题，提出一种基于滑动数据窗的固有频率筛选方法。两种不同频率变化规律的数值仿真算例验证了辨识算法的有效性，辨识结果精度得到了提升。通过对高温环境下的热防护结构的时变伪固有频率进行辨识，验证了筛选方法的有效性。

1 NIC子空间跟踪算法与时变模态参数辨识

1.1 输入量的迭代更新

由于基于NIC的子空间跟踪方法是采用递推最小二乘算法求解其中的子空间优化问题，因此振动信号的前处理是必需步骤。考虑线性时变系统离散时间状态空间模型

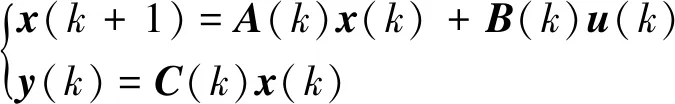
(1)

其中：x(k)∈Rn×1为第k个采样时刻的系统状态向量；n为系统阶次；A(k)∈Rn×n为k～k+1时刻的系统状态转移矩阵；B(k)∈Rn×m为第k时刻的输入矩阵；u(k)∈Rm×1为第k时刻的m维输入向量；y(k)∈Rr×1为第k时刻的r维响应向量；C(k)∈Rr×n为第k时刻的输出矩阵。

利用k时刻附近的输入输出数据可组成相应的广义Hankel矩阵

(2)

其中：M为广义Hankel矩阵的块行数。

对应地，下一时刻的广义Hankel矩阵为

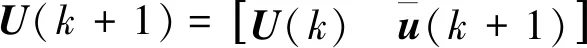
(3)

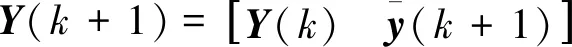
(4)

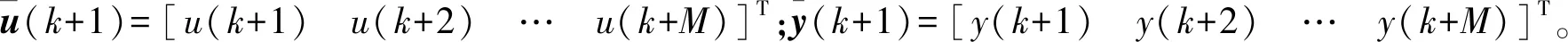
根据文献[8]提出的数据迭代更新规则，令

得到子空间跟踪输入量z(k)的迭代更新形式

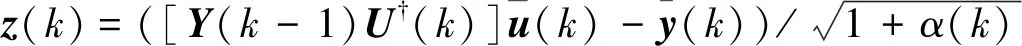
(7)

其中：上标符号“†”代表矩阵伪逆。

式(5)和式(7)中的[U(k-1)UT(k-1)]-1以及[Y(k-1)U†(k)]更新形式分别为

通过以上公式可得到满足子空间跟踪算法要求的输入数据z(k)，且有

其中：Γ(k)为k时刻的能观矩阵。

通过对Y(k)U⊥(k)进行奇异值分解，得到

Y(k)U⊥(k)=R(k)Σ(k)V(k)T

(9)

则R(k)的前n列组成的矩阵即为能观矩阵Γ(k)，同时也是矩阵Y(k)U⊥(k)的信号子空间W(k)。通过寻找合适的跟踪算法可以避免计算量较大的奇异值计算步骤，达到节省计算量的目的。

1.2 NIC子空间跟踪

NIC算法将子空间跟踪视为无约束优化问题，NIC算法选取的目标方程为

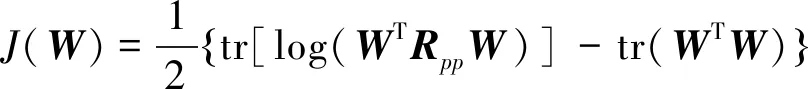
(10)

其中：W为信号子空间矩阵；tr为矩阵的迹；Rpp=E[ppT]为输入量的协方差矩阵。

J(W)对W的梯度可以写为

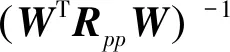
(11)

根据梯度上升规则，W(k)的迭代更新规则可写为

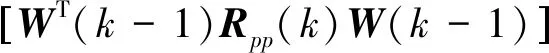
(12)

其中：η为学习步长。

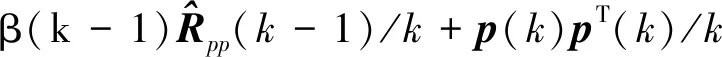
(13)

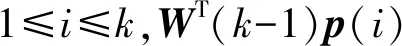
(14)

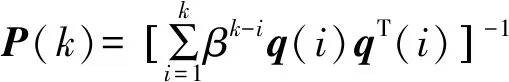
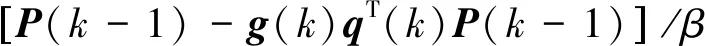
(15)

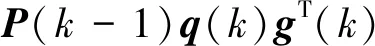
(16)

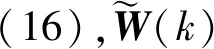
(17)

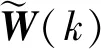
初始化步骤：

1) 令P(0)=δIr，其中：δ为一个正小量；Ir为r×r单位矩阵；

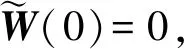
3)W(0)通过式(9)进行计算。

迭代更新步骤：

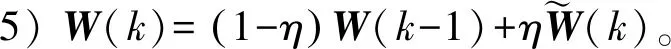
1.3 时变模态参数提取

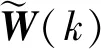
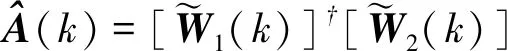
(18)

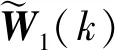
对系统矩阵的估计进行特征值分解，得到

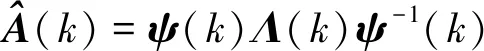
(19)

其中：ψ(k)为特征向量矩阵，Λ(k)=diag(λ1(k),…,λn(k))为特征值对角矩阵。

由此可以求得k时刻第i阶伪固有频率ωi(k)和伪模态阻尼比ξi(k)分别为

其中：上标“R”表示取特征值的实部；Δt为数据采样间隔。

2 仿真算例

为验证所提出算法的有效性以及抗噪能力，对如图1所示的两自由度弹簧-质量系统进行辨识。

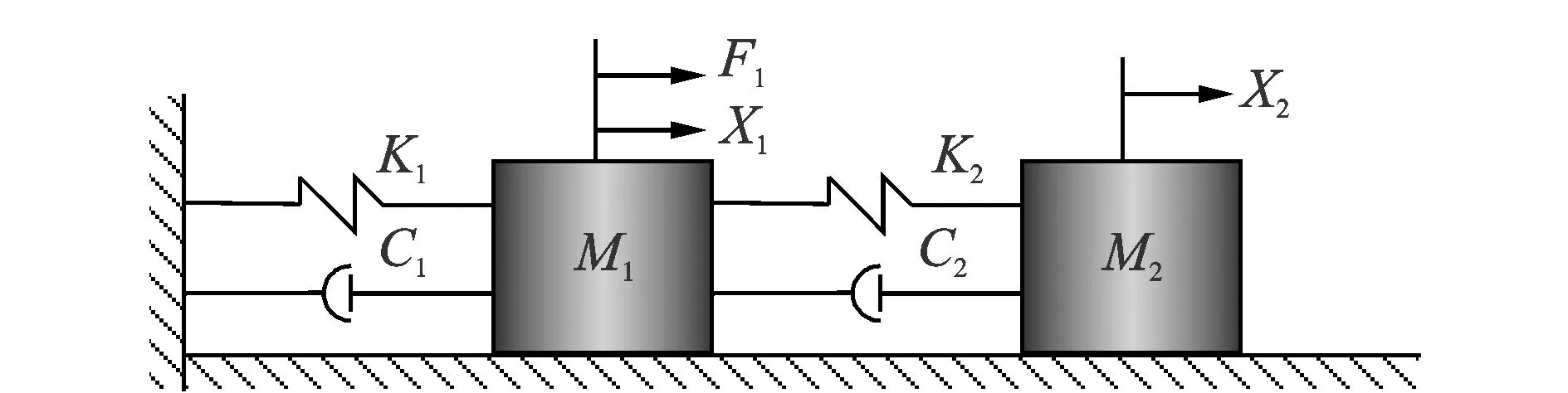
图1 2自由度弹簧-质量系统示意图Fig.1 Schematic diagram of the 2-DOF spring-mass model

该弹簧-质量系统的运动控制方程为

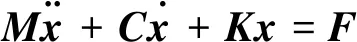
(21)

质量矩阵M为

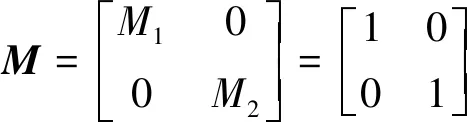
(22)

刚度矩阵K为

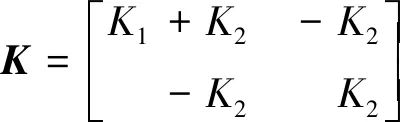
(23)

阻尼矩阵C为

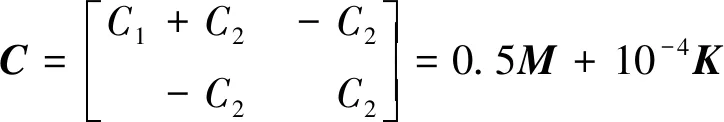
(24)

为了研究所提出的方法对不同频率变化模式的适用情况，对刚度为指数变化和刚度为正弦变化两种情况进行讨论。

2.1 刚度为指数变化的情况

为模拟频率为指数变化的模式，式(23)中的各刚度取值为K1=1 000exp(-0.4t)，K2=2 000。仿真计算采用的时间步长Δt=0.001 s。分别采用文献[12]和笔者提出的辨识方法进行辨识，为模拟真实的测量情况，结构响应中加入一定量的噪声。两种方法均采用相同的计算参数，结构响应信号信噪比(signal to noise ratio，简称SNR)为10时，辨识结果如图2，3所示。可以看出，PAST和NIC方法都能很好地跟踪频率变化。在初始时刻，PAST的误差较大，而NIC算法的结果更接近理论参考值。在跟踪过程中，PAST算法结果呈现出较大的离散性，而NIC算法的结果相对比较平滑。为了量化评估在不同信噪比条件下两种算法的计算结果，引入平均绝对误差率(mean absolute percentage error，简称MAPE)

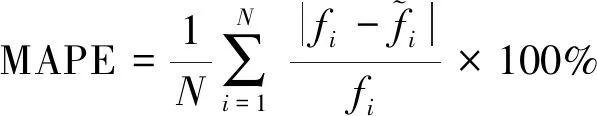
(25)

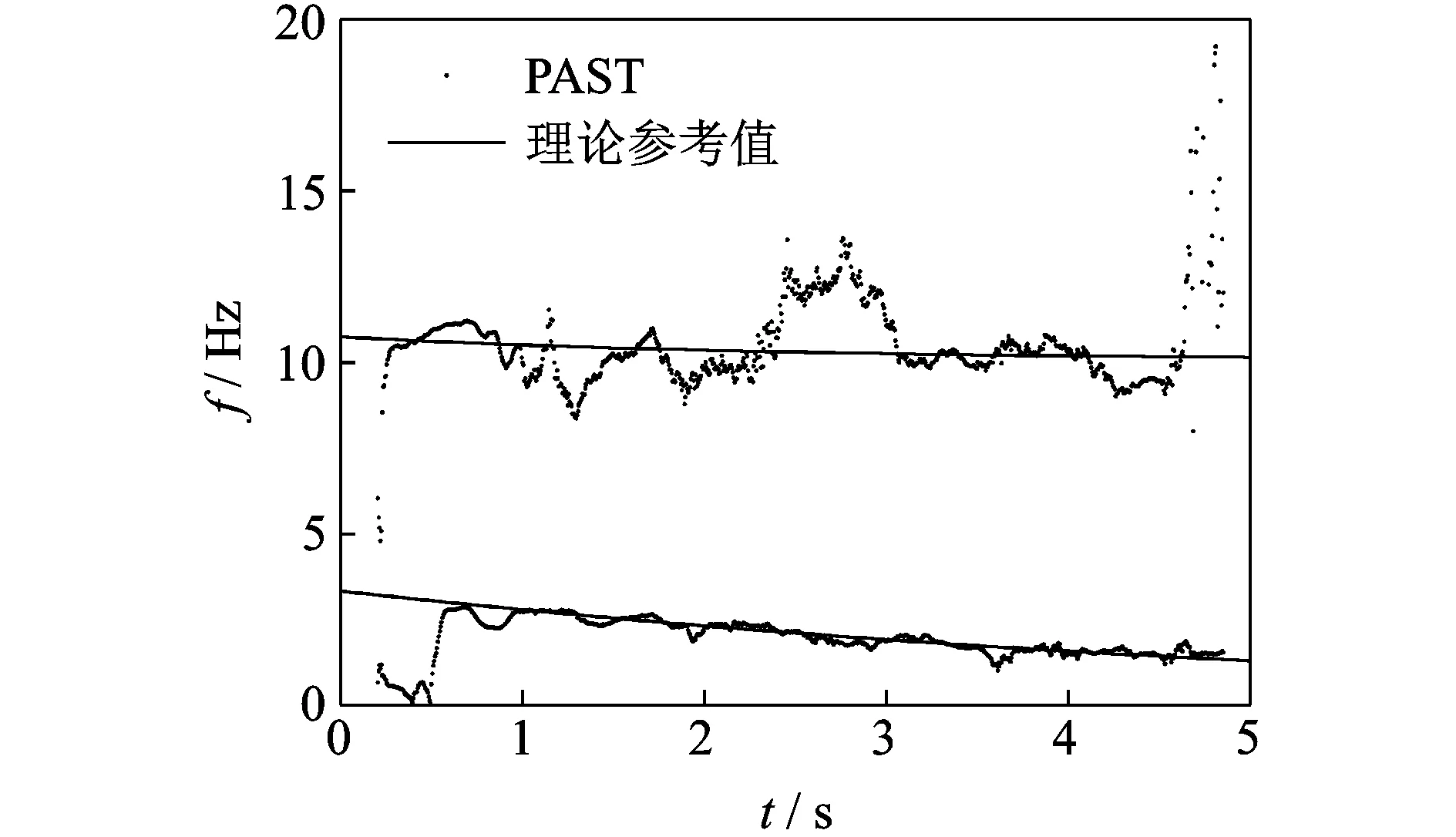
图2 PAST辨识结果与理论参考值对比(第1组)Fig.2 Comparison of the results by PAST algorithm and reference results (the first group)

图3 NIC辨识结果与理论参考值对比(第1组)Fig.3 Comparison of the results by NIC algorithm and reference results (the first group)

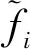
通过两种算法5次计算得到系统固有频率的MAPE误差取均值如表1所示。可以看出，当结构响应信号的信噪比较高时，两种算法的MAPE误差相差不大。随着噪声量的增加，PAST算法的MAPE误差呈现出大幅增加的趋势，NIC算法辨识误差虽然也有增加，但是仍然优于PAST算法的辨识结果。

表1 辨识结果MAPE比较(第1组)

Tab.1MAPE comparison of the identified results(the first group)%

SNRPASTNIC第1阶第2阶第1阶第2阶5011.404.2910.243.722011.745.8210.403.921011.896.3410.805.70512.2412.9110.838.67

2.2 刚度为正弦变化的情况

式(23)中，刚度取值为K1=2 000+1 000×sin(πt/5)，K2=2 000，仿真计算的时间步长Δt=0.01 s。信噪比为5时的辨识结果如图4，5所示。可以看出，两种算法对正弦形式的频率变化都可以很好地跟踪辨识，两种算法结果差异不大，在个别位置如2 s时刻左右，NIC算法得到的结果较PAST算法得到的结果更接近理论参考值。

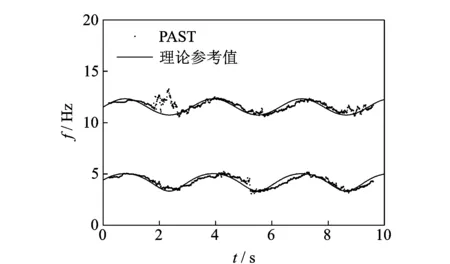
图4 PAST辨识结果与参考值对比(第2组)Fig.4 Comparison of the results by PAST algorithm and reference results (the second group)

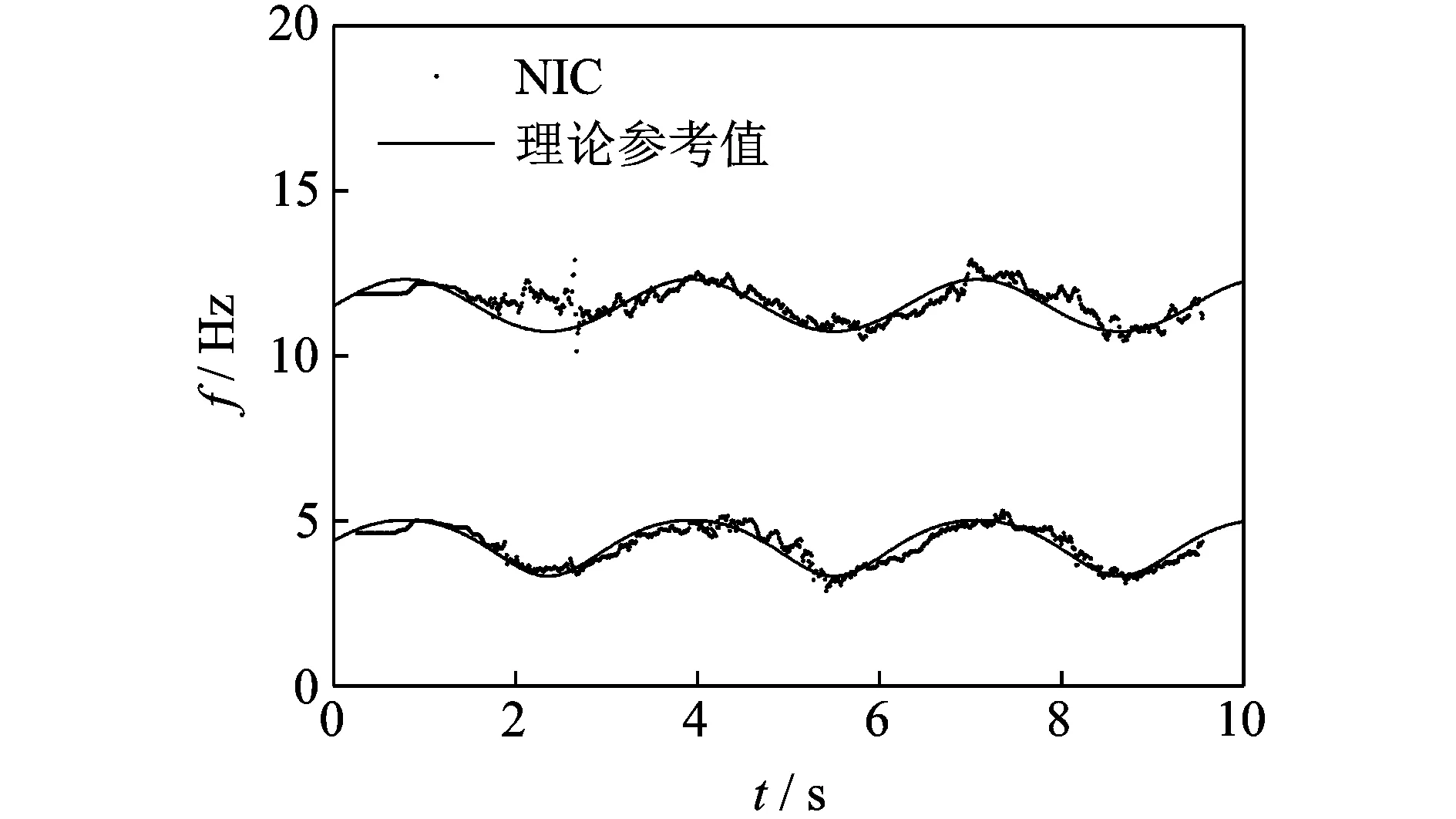
图5 NIC辨识结果与理论参考值对比(第2组)Fig.5 Comparison of the results by NIC algorithm and reference results (the second group)

不同信噪比情况下得到的MAPE误差如表2所示。可以看出，两种方法的识别结果误差都在10%以内，在添加了20%的噪声以后都可以保证很好的识别精度，NIC算法在不同SNR情况下的识别结果误差均不同程度地优于传统的PAST算法。

表2 辨识结果MAPE比较(第2组)

Tab.2MAPE comparison of the identified results(the second group)%

SNRPASTNIC第1阶第2阶第1阶第2阶504.821.524.131.35204.931.854.271.70105.211.914.591.8455.512.594.992.67

3 实验验证与应用

飞行器热防护结构在温度变化环境下的振动特性一直受到研究人员的关注，这里对一块陶瓷基复合材料热防护板的伪固有频率进行辨识。热防护结构悬吊在刚性结构上，加热面通过远红外热辐射加热至800℃，冷端此时温度为80℃，停止加热使热防护结构自然降温。在冷端通过激振器施加可视为高斯白噪声的随机载荷，并由4个加速度传感器进行数据采集，采样频率为1 400 Hz。实验装置如图6所示。

图6 实验装置图Fig.6 Image of the experiment setup

利用NIC方法对伪固有频率进行辨识，计算参数Hankel矩阵的块行数M=100，遗忘因子β=0.94，辨识结果如图7所示。可见，大部分辨识结果都聚集在220，300和440 Hz左右，其他点可视为由于测量噪声等原因导致的虚假模态。

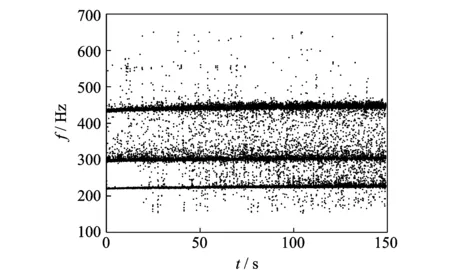
图7 NIC方法辨识结果Fig.7 Identified results using NIC algorithm

采用比较筛除的方法剔除虚假模态点，定义一个加权平均伪固有频率为

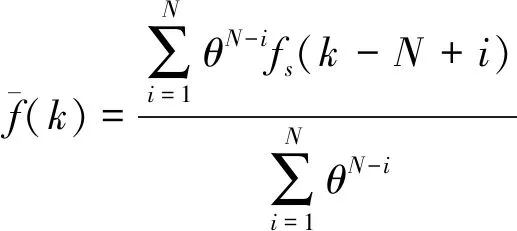
(26)

其中：θ为加权因子；fs(k)为经过筛选的k时刻的伪固有频率。

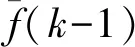
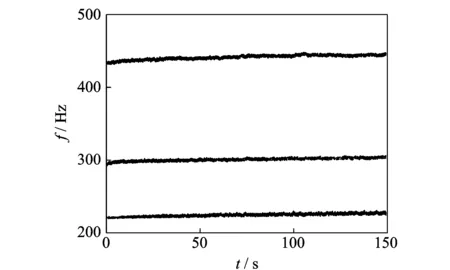
图8 筛选后的辨识结果Fig.8 Identified results with selection and sifting procedure

图8为筛选后的辨识结果。可以看出，自由状态下热防护结构从800℃自然降温的150 s内，前3阶固有频率分别由221，295，434 Hz升至230，304，444 Hz。经过筛选算法处理的结果不再包含虚假模态，结构的时变趋势更加容易分辨。

4 结束语

提出了一种基于NIC子空间跟踪算法的伪固有频率辨识方法，通过一个两自由度弹簧-质量系统两种不同频率变化形式的仿真数值算例，验证了算法的有效性。数值算例表明，该方法在低SNR情况下仍有较好的辨识结果。与传统的PAST方法相比，该方法辨识结果与理论参考值更接近，具备更高的识别精度。针对时域辨识算法常见的虚假固有频率问题，从辨识结果后处理的角度出发，提出了一种虚假固有频率剔除方法。该方法具备计算量小、计算所需参数少的特点。最后，识别了飞行器热防护结构降温过程的伪固有频率变化过程。实验结果表明，该方法处理效果明显，所提出的辨识方法和后处理方法具备较高的应用价值。