高聚物粘结炸药动态损伤破坏的数值刻画

魏强， 黄西成， 陈刚， 陈鹏万

(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.中国工程物理研究院 总体工程研究所, 四川 绵阳 621999)

0 引言

颗粒粘结炸药在低速撞击等环境下可能发生点火，一般情况下，不会发展成为爆轰，但仍会对人员和器材设备形成威胁[1]。高聚物粘结炸药(PBX)的这种机理尚不明确的点火行为与其内部损伤的形成息息相关[2-4]，刻画PBX炸药的损伤及其演化过程存在着很多困难。从试验的角度来讲，炸药内部损伤过程难于捕捉，且存在随机性(由于初始缺陷的随机性分布)；此外，在描述炸药的破坏时也缺乏合适的表征参量，来建立材料细观破坏形式与材料宏观力学响应之间的联系。从数值仿真的角度来讲，首先需要解决的就是所用数值方法本身在描述材料宏、细观破坏时存在的局限性以及伴随引入的虚假数值结果图像(如应变局部化问题)；其次需要解决的就是建立能正确刻画材料力学行为的本构模型。由于存在上述困难，且不易解决，因而现今对PBX炸药损伤破坏过程的研究主要是捕捉一些破坏图像，增进对相关破坏过程的认识[5-7]。

相比于试验手段，数值仿真能提供更多的过程信息，这对炸药安全性的评估是有利的；商业有限元软件的广泛应用也为数值仿真研究提供了很大的便利。但PBX炸药具有明显的黏弹性，拉伸、压缩不对称性，压力相关性，应变率相关性，温度相关性等[8]，此外，其变形破坏过程中可能还会伴有明显的化学反应过程[9]，这些复杂的特性使得PBX炸药的力学行为难于刻画，更没有现成的本构模型可用。由于PBX炸药的宏观力学响应形态与混凝土材料类似，而混凝土材料模型经过多年的发展已经形成了一套较为完备的描述体系，因此借鉴混凝土材料模型来描述PBX炸药的力学行为成为最常用的方法之一[10-12]。相较而言，PBX炸药的力学行为比混凝土材料更为复杂，借鉴混凝土材料的本构模型主要是用来刻画PBX炸药在复杂应力及应变率影响下的力学行为；为了更真实地描述PBX炸药的力学行为，仍需要对现有的混凝土本构模型进行进一步的发展。

本文在有限元分析软件AUTODYN中，以Karagozian & Case (K&C)模型[13]框架为基础，依据PBX炸药的力学特性对模型进行了修改和扩展。在修改的模型基础上，分析了材料的应变率效应及损伤破坏的描述方法等，以期较好地描述低速撞击等环境下PBX炸药的损伤破坏，为后续炸药安全性评估研究提供基础。本文的研究对象为法国原子能委员会研究人员研究的某奥克托今(HMX)基PBX炸药，其力学行为类似于PBX9501[11].

1 本构模型

1.1 压力依赖性

本文采用的模型考虑了PBX炸药力学行为的压力依赖性。模型以K&C模型的框架为基础，修改了原K&C模型中的损伤演化模式，计及了材料强度、模量、损伤演化模式等的压力依赖性。

与很多地质类材料本构模型的构造方法相同，模型采用了不同强度面插值的方法来描述材料当前的屈服强度，强度面间的插值函数是用户输入的损伤演化曲线。此处采用一条应力σ- 应变ε曲线来说明模型的描述方法。用于插值的不同强度面在应力- 应变曲线中体现为不同的特征点，如图1所示。模型中采用3个特征点来刻画材料的应力- 应变曲线，分别是初始屈服点(材料线性弹性段和非线性硬化段的临界点)、最大应力点(材料硬化过程和软化过程的临界点)、残余应力点(表征材料破坏后的残余承载能力)。

图1 材料应力- 应变曲线示意图Fig.1 Stress-strain curve

在初始屈服点之前材料处于弹性变形阶段，当应力超过初始屈服点后，模型即认为材料开始了损伤演化；当前屈服点由最大应力点与初始屈服点或残余应力点通过非线性插值来确定。损伤演化曲线作为非线性插值函数参与了当前屈服点的确定，其主要作用是建立应力和应变之间的联系，它是由材料单轴压缩应力- 塑性应变曲线(初始屈服点至残余应力点段)做无量纲处理后获得的。为了考虑复杂的应力状态，3个特征点的应力信息在应力空间内形成了3个强度面，而应变信息则是通过损伤演化参量来考虑应力状态的影响的。通过损伤演化曲线应力和应变信息之间建立起了联系，这样，模型就能完整地描述材料在不同应力状态下的应力- 应变响应。

3个特征点在空间形成的最大强度、残余强度、初始强度3个强度面可以分别表示为

(1)

(2)

(3)

式中：a0、a1、a2、a1f、a2f、a0y、a1y、a2y均为待定参数；p为静水压力(取压缩为正，拉伸为负)。

材料当前的屈服强度可通过上述3个强度面插值得到，用方程表述为

(4)

式中：λ为损伤演化参量；η(λ)为损伤演化曲线(用于非线性插值)；λ1对应于η(λ)刚达到1时的λ值。损伤演化参量λ的表达式为

(5)

式中：εp为塑性应变；r为应变率增强因子；εm为不同约束压力pa下材料的最大失效应变(对应于不同约束压力下材料的最大强度)，与压力相关。

在约束压力较低时，上述描述方法已经可以较好地描述材料的应力- 应变响应。但当约束压力大于脆延转化压力后，试验结果显示，材料的应力- 塑性应变曲线不再出现软化现象(见图2)。这时，当λ>λ1后，材料的损伤演化过程就无法再采用(4)式来描述，需要重新给出描述方法。为了解决这个问题，需要对K&C模型进行修改，具体为在高约束压力下，取消原模型中的软化插值过程，引入一个简单的线性硬化过程，即认为在较高约束压力下，材料后期会进入一个线性硬化阶段，模型也直接变为塑性线性硬化模型(硬化模量依赖于约束压力)。这样，以材料的脆延转化压力为界，模型中相当于构造了两种类型的损伤演化曲线，用来描述材料在不同约束压力下的应力- 应变响应(存在软化现象和不存在软化现象)。

图2 不同约束压力下PBX炸药的应力- 塑性应变曲线[9]Fig.2 Stress-plastic strain curves of PBX explosives under different confined pressures[9]

在选择采用的损伤演化曲线时，模型中采用了约束压力的概念，与静水压力不同，约束压力不会随着单向压缩加载而发生变化，如单轴压缩过程中，约束压力始终为0 MPa. 约束压力概念的引入对描述材料模量的压力相关性至关重要，显而易见，材料模量的变化不可能与静水压力形成一一对应的关系。模型中，约束压力定义为

pa=p-Δσa/3，

(6)

式中：Δσa为单向压缩加载路径上(单轴压缩与静水压力组合形成的加载路径)的von Mises等效应力值。在单向压缩情况下，这种定义无疑是正确的；对于其他复杂应力状态，约束压力的定义是一种等效。上述模型成功地捕捉到了PBX炸药在不同约束压力下的应力- 应变响应。

1.2 应变率效应

图3 不同应变率下材料强度随压力的变化情况[14]Fig.3 Variation of material strength with pressure under different strain rates[14]

本文中采用径向应变率增强的方式来描述材料的应变率效应，通过图3中的字母标识，对这种应变率增强方式进行说明：假设点C当前的压力为G，模型中认为这是应变率增强后的压力，首先通过当前的应变率增强因子(通过当前应变率得到)把压力缩小，得到对应准静态时的压力D，进而得到准静态时的强度E；再通过应变率增强因子放大，得到应变率增强后的强度F，作为点C的强度值。由几何相似性不难证明，当材料强度随压力的变化为直线时(如图3中所示的情况)，径向应变率增强方式得到的结果与图3中的试验结果相一致；但是从本文采用的试验数据[9,11]来看，在更宽的压力范围内，PBX炸药的强度随压力近似呈双线性变化，Wiegand等[15]就曾建议直接采用双线性方程来描述PBX炸药强度随压力的变化情况。为了方便介绍，图4中比照图3给出了较大压力范围内PBX炸药强度随压力变化的示意图，线段na和ab对应于准静态时的情形，点n对应的强度为材料的单轴压缩强度。

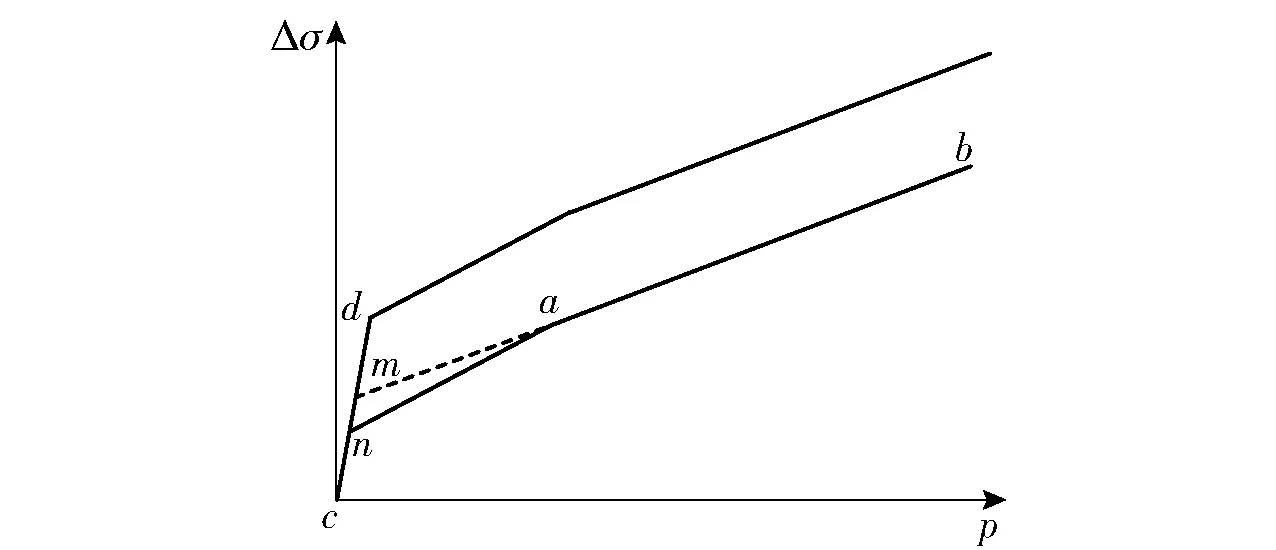
图4 应变率效应修正说明示意图Fig.4 Schematic diagram of correction of strain rate effect

如图4所示，在较高约束压力下(压力达到ab段时)，PBX炸药材料强度随压力变化的斜率会减小，这时，径向应变率增强的方式会高估材料的应变率增强效应(径向应变率增强的方式等价于斜率不变的情形)。本文对较高压力下材料的应变率增强效应进行了修正，径向应变率增强的方式形式简洁，实现方便，本文不作改动，修正的主要是应变率增强因子。在图4中，延长ab段与cd段(单轴压缩路径)相交于点m，对mb段而言，这就构造出了与图3类似的情形，不过此时交点m对应的强度不再是材料的单轴压缩强度。对应于ab段新的应变率增强因子可表示为

rn=1+(ro-1)fc/σm，

(7)

式中：fc为材料的单轴压缩强度；ro为未修正前的应变率增强因子；σm为点m对应的强度值。本文中，压缩时的动态增强因子rc采用了文献[14]中的试验数据：

(8)

由于没有在公开文献中查到法国原子能委员会研究人员在动态拉伸方面的研究工作，因而拉伸时的动态增强因子rt采用了文献[16]中与之力学行为类似的PBX9501试验数据：

(9)

除了材料强度与应变率相关外，本文中还假设材料的剪切模量与应变率增强因子成正比；而对于材料的最大失效应变，本文中认为其与应变率无关[17]。图5给出了不同应变率增强因子下，材料的单轴压缩应力- 应变曲线(由单个六面体单元计算输出)，计算结果可以直观地展示出上述假定。

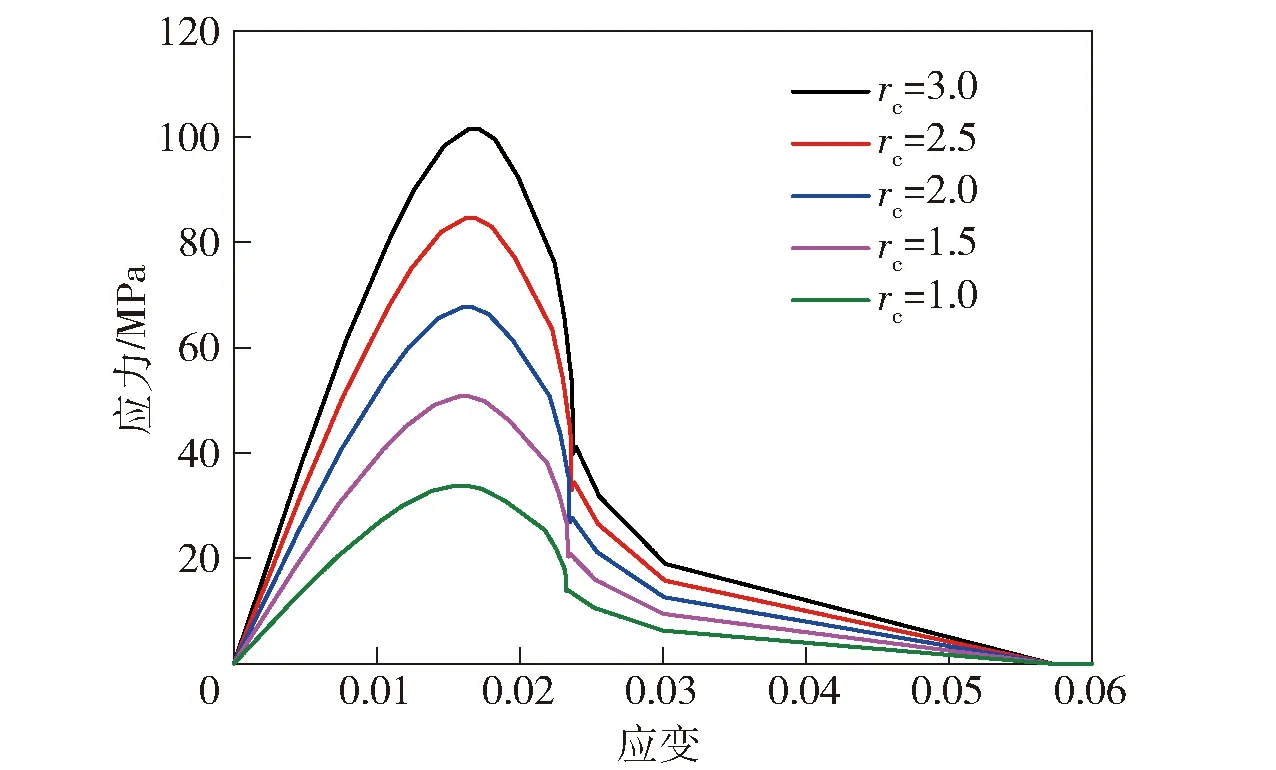
图5 单轴压缩应力- 应变曲线随动态增强因子的变化Fig.5 Variation of stress-strain curves in uniaxial compression with dynamic enhancement factor

1.3 偏平面形状的描述

材料偏平面形状由类三角形向圆形转变的过程，也是材料由低约束压力下的脆性行为向高约束压力下的塑性行为转变的一种体现。K&C模型中经验性地给出了混凝土材料拉伸、压缩子午线之比(偏平面形状变化的依赖量)随压力变化的公式；把PBX炸药的材料参数带入到公式中发现，在单轴压缩时，材料的拉伸、压缩子午线之比已经达到0.90，即偏平面形状已接近圆形，显示出了明显的塑性材料的特性，这与PBX炸药的力学特性不相符(在单轴压缩情况下，PBX炸药材料体现出明显的脆性特性)。

对于PBX炸药在复杂应力下力学特性的试验研究还很缺乏。唐维[18]对某PBX代用材料开展了相关试验研究，根据试验结果，在低约束压力下，材料拉伸、压缩子午线之比近似为2/3[19]，这与Riedel-Hiermaier-Thoma模型中建议的0.680 5相近[20]。本文中取0.68作为约束压力较低时，材料拉伸、压缩子午线的比值。随着约束压力变大，材料偏平面的形状逐渐变为圆形，即拉伸、压缩子午线之比逐渐变为1.00，本文中把炸药晶粒屈服强度的值(HMX晶粒的屈服强度为130 MPa[21])作为此转变压力。这里隐含一假设，即炸药晶粒本身的屈服强度没有明显的压力依赖性。PBX炸药在受拉时体现出明显的脆性特性，因而当压力为负时，本文沿用K&C模型中的建议，把拉伸、压缩子午线之比取为0.50. 本文中采用的拉伸、压缩子午线之比可归纳为

(10)

式中：σY为炸药晶粒的屈服强度。各点间采用线性插值过渡。

2 结构破坏中材料损伤的描述

2.1 变形局部化

采用有限元方法描述材料损伤和破坏过程时存在困难，面临的困难之一是对材料软化过程地描述。材料在应变软化过程中会出现变形局部化的问题，这在岩土材料本构模型的研究中有过很多的讨论[22]，其本质是软化过程中材料变形地高度不均匀化。试验中得到的材料应力- 应变响应的软化段既包含了材料本身的力学特性，同时也包含了变形局部化后引入的结构效应。Wang等[23]就曾采用局部化结构特征与材料力学特性相结合的方法对某PBX代用材料的单轴压缩应力- 应变曲线进行了描述，与试验结果符合得很好。遗憾的是，大多数试验研究中，一般只给出了材料的应力- 应变曲线，很少对试件破坏后的形貌进行描述，这对试验数据的理解造成了一定的困难。

网格划分的尺寸、计算中的数值误差等同样会导致数值计算中出现结构变形的局部化，这类似于试验中出现的变形局部化，但产生的原因不同。为了减小这种不真实的变形局部化，除了要保证合适的计算网格尺寸外，还需要在单元中引入特征长度来解决。常见的引入方法有两种[24]：方法1是采用非局部化模型的形式，其基本思想是，在给定的特征长度内(不受单元尺寸的约束)基于单元的积分点对塑性应变等参量进行平均化处理，从而引入特征长度的影响，避免数值上导致不真实的变形局部化；方法2是采用断裂能加特征长度的形式，就其实际效果来看，相当于调整应力- 应变曲线的软化段(下降段)，人为减缓单元的软化速度，以此来避免有限元计算中出现的变形局部化问题。方法1需要计算程序中相关算法的支持，而方法2仅需调节材料的参数就可实现。

特征长度本意是用来定义材料变形局部化的尺度，如材料在破坏过程中形成的裂缝尺寸等。但在实际破坏过程中，裂缝尺寸受到应变率、应力状态等很多因素的影响，导致很难给出合适的特征长度。本文中没有直接引入特征长度的概念，而是通过调整应力- 塑性应变曲线的软化段来近似考虑。结合模型的特点，调整时保持了应力不变，只对软化段对应的塑性应变部分进行调节。采用单轴压缩试验进行校验，压缩试件分为6 mm×6 mm×12 mm的长方体和φ6 mm×12 mm的圆柱体两种，压头和试件的接触面不考虑摩擦。计算中，试件网格尺寸考虑了1.5 mm、1.0 mm和0.5 mm 3种。计算结果显示，当下降段塑性应变放大为原来的4倍时，输出结果与试验结果取得了较好的一致性，如图6所示。

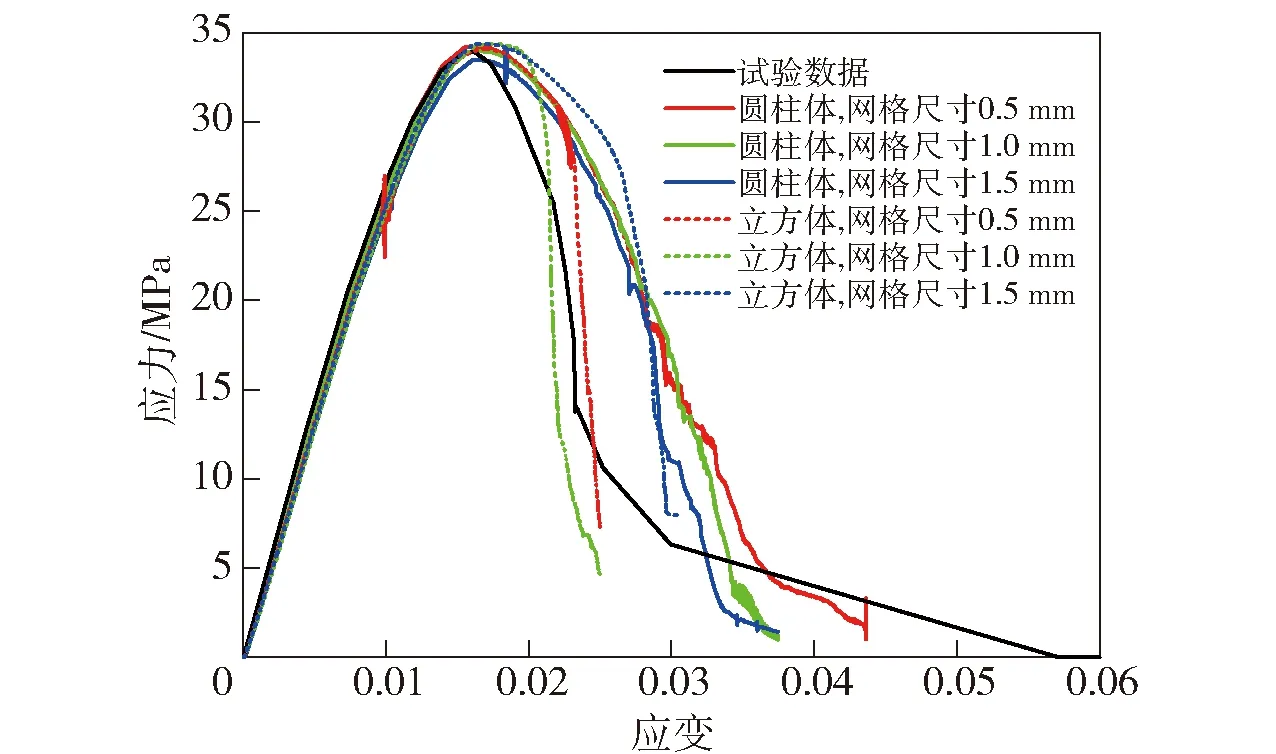
图6 单轴压缩应力- 应变曲线计算与试验结果的对比Fig.6 Comparison of calculated and experimental stress-strain curves of uniaxial compression

计算结果同时显示出，即使网格的大小和压缩试件的形状有所不同，材料应力- 应变曲线的硬化段依然保持了很好的一致性，而软化段就出现了明显的分散性。相比而言，采用圆柱型试件得到的软化段一致性要更好一些。

2.2 拉伸失效后的处理

对失效单元的处理是采用有限元方法描述材料损伤和破坏过程时面临的另一个困难。单元的失效在程序实现时等同于单元的删除，这会在结构中形成一个尺度虚假的裂纹，从而影响结构的后续响应。PBX炸药易于产生拉伸断裂，如果程序中不考虑拉伸破坏的话，就无法表征材料的破坏形貌；但如果仅把拉伸破坏的单元作常规失效处理的话，又会对结构后续的压缩响应造成明显的影响。为了更好地表征PBX炸药材料，需要对拉伸失效后单元的处理方式进行修正。

AUTODYN软件中有一种失效后可再次恢复承载能力的单元失效处理方式，遗憾的是在进行程序二次开发时这种失效方式无法直接调用。借鉴这个思路，本文对拉伸失效作如下处理：单元中的应力达到拉伸强度时，把单元的剪切模量和屈服强度置为小量(原数值的十万分之一)，并把此单元设置为拉伸失效状态进行输出显示；当拉伸失效单元重新承受压缩载荷时，单元恢复压缩承载能力，即认为拉伸失效不会对单元的压缩过程产生影响。本文在描述材料的拉伸破坏时，没有考虑拉伸过程中的损伤演化，认为当单元中的应力达到拉伸强度后，材料直接发生脆性断裂。

采用单个六面体单元对程序的执行情况进行检查。单元一端加载，另一端限制加载方向的自由度；加载端进行拉伸- 压缩- 拉伸- 压缩的反复加载过程，输出的应力- 时程曲线如图7所示。第1次拉伸过程，让单元进入了拉伸失效，随后的压缩加载过程，单元完全恢复了承载能力，响应与材料的单轴压缩过程完全一致；第2次进入拉伸过程后，单元中的应力首先进行了卸载，当应力卸载为0 MPa时，单元中的应力不会随着拉伸载荷的增大而增长，即单元已经失去了拉伸承载能力；当单元再次进入压缩过程时，单元先是经历弹性加载，当应力到达当前的屈服强度后，应力响应沿着上次的压缩损伤路径继续演化。单元是通过速度边界条件进行加载的，加载过程没有考虑应变率效应。图7中标示的虚线位置为拉伸、压缩加载发生转化的时刻。

图7 拉伸- 压缩- 拉伸- 压缩加载过程的应力- 时程曲线Fig.7 Stress-time history curve of tension-compression-tension-compression loading process

在实际的应用中发现，这种拉伸失效单元的处理方法易受单元变形情况及应力状态的影响，在考虑拉伸裂纹扩展的算例中，该方法并不适用。

3 Steven试验仿真计算

3.1 计算模型介绍

法国原子能委员会研究人员通过试验手段研究了某PBX炸药(力学行为类似于PBX9501炸药)的力学特性及其安全性[9，11，14,25-26]，研究给出了不同约束压力下PBX炸药的应力- 应变响应，模量的压力相关性，材料的应变率效应等一系列的试验结果。在采用Steven试验研究炸药的点火问题时，还对未发生点火的炸药试样进行了解剖观察，给出了试样在撞击后的破坏变形形貌。本文就采用这一系列的试验结果，来考察模型对PBX炸药在撞击作用下损伤破坏情况的刻画能力。

下面对Steven试验的计算模型进行简要的介绍，模型中：撞击弹头质量1.2 kg，撞击速度为58 m/s，材料为钢；靶体为φ200 mm×35 mm的圆柱型钢盒，撞击端面钢层的厚度为3 mm，钢盒内含有φ100 mm×13 mm的圆柱型PBX炸药试件及内径为100 mm、外径为120 mm、厚度同样为13 mm的有机玻璃环。计算模型如图8所示，炸药试件的网格尺寸控制在1 mm左右。计算中，钢采用了理想弹性塑性模型来描述，有机玻璃采用了弹性模型来描述，具体参数参见文献[11]。

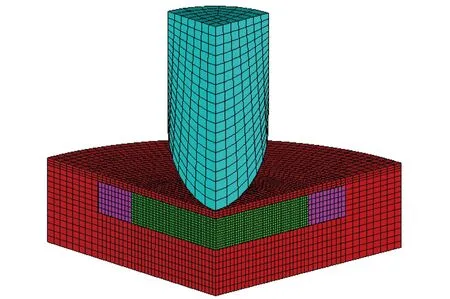
图8 Steven试验计算模型Fig.8 Numerical simulation model of Steven test

为了更好地描述试验数据，本文对PBX炸药的强度面进行了分段拟合，炸药本构模型中强度面的参数如表1、表2所示(在高约束压力下材料不会发生软化，因而表2中没有残余强度面的参数)，试验数据参考文献[9，11]。本文中采用的损伤演化曲线根据文献[9]中的试验数据获得，得到的曲线如图9所示，图中η为采用材料单轴压缩强度归一化后的应力(硬化段部分取初始屈服强度时η=0，取最大强度时η=1)。计算中，炸药的剪切模量和体积模量考虑了材料的压力相关性，试验数据取自于文献[25]，如图10所示。

表1 约束压力小于100 MPa时强度面的参数

表2 约束压力大于100 MPa时强度面的参数

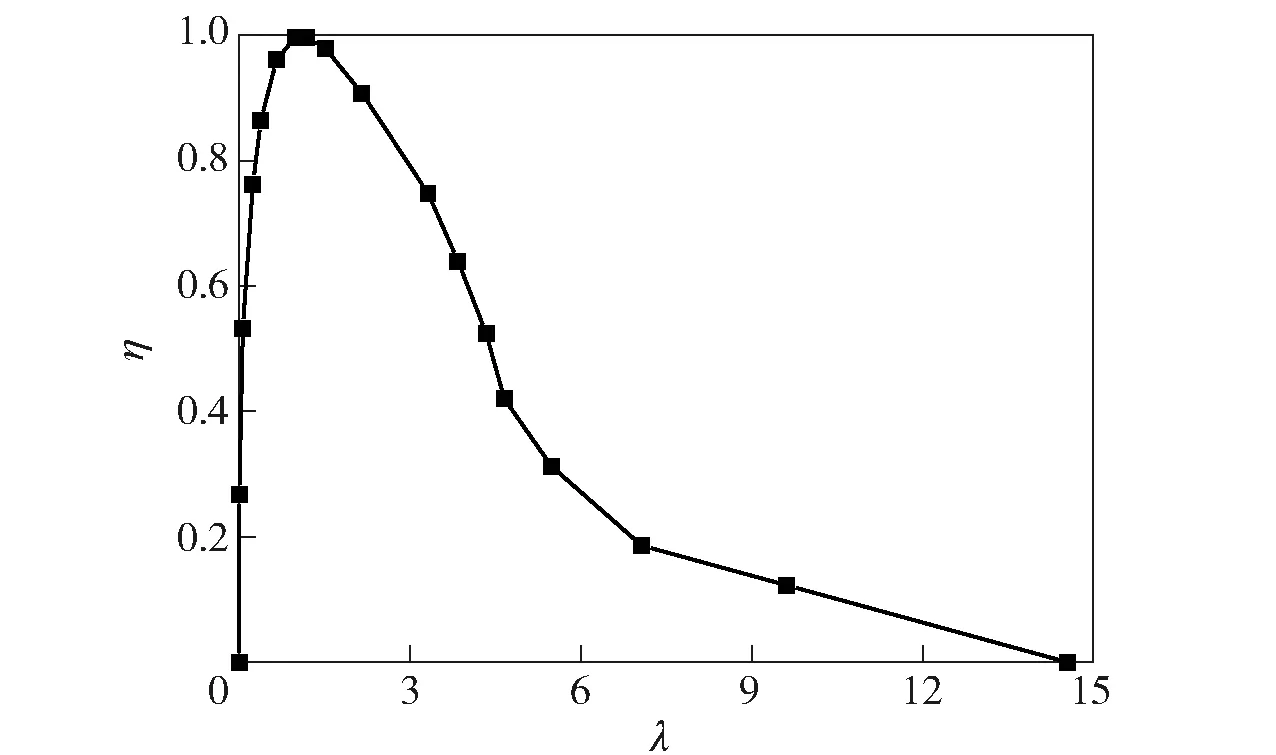
图9 损伤演化曲线Fig.9 Damage evolution curve

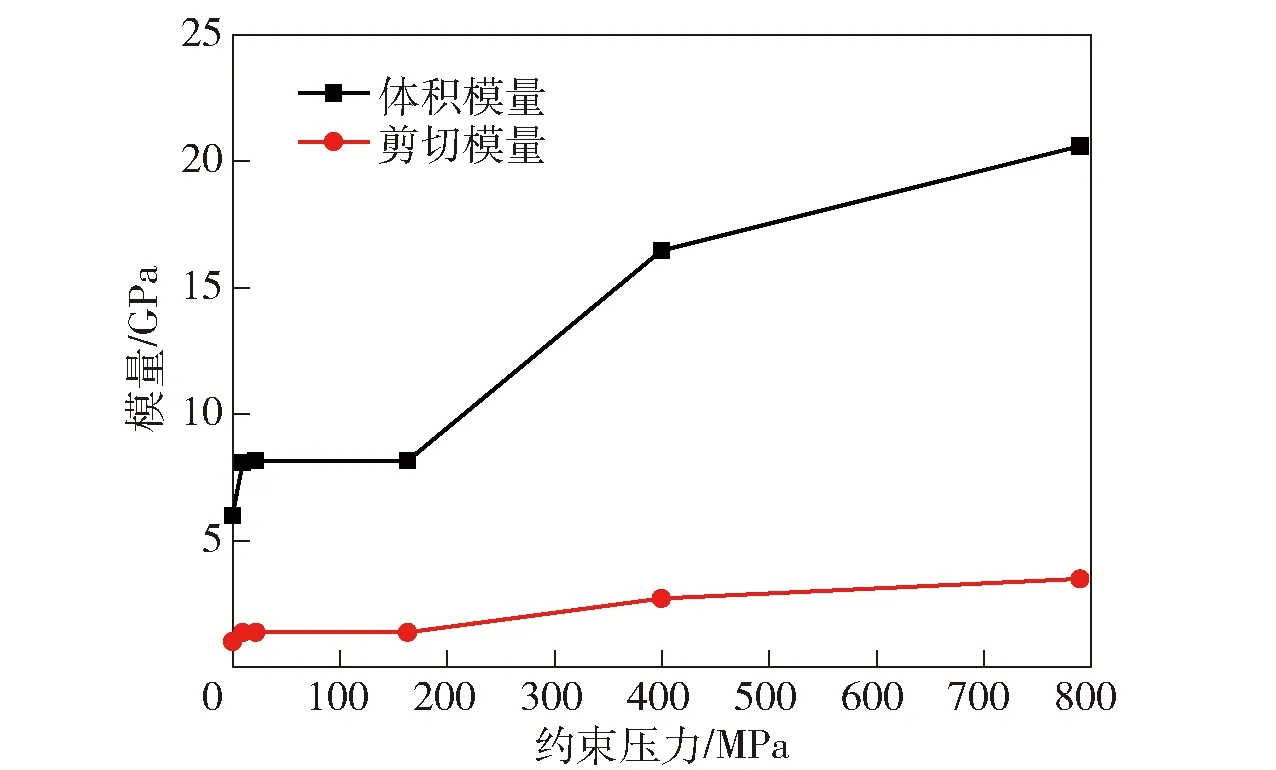
图10 模量随约束压力的变化Fig.10 Variation of modulus with confined pressure

3.2 计算与试验结果对比

撞击后炸药的变形形貌如图11所示，在撞击成坑部位，模型很好地捕捉到了坑体的形貌。同样，模型也成功捕捉到了炸药试件的隆起变形，但计算结果在数值上与试验结果存在差距。隆起过程涉及到材料的破坏、滑移及由此引起的体积膨胀等问题，主要是材料的局部化变形过程，采用有限元方法进行描述时存在困难。虽然没有很好地描述到材料的隆起变形，但模型仍捕捉到了试件中的一些破坏形态，如隆起过程中形成的剪切破坏、炸药试件靠近有机玻璃部分底部的翘起现象等。

图11 撞击后炸药试样变形情况Fig.11 Deformation of explosive specimen after impact

文献[15]给出了撞击后试样(同类PBX炸药的代用材料)背面典型的破坏形态，数值计算结果与其对比如图12所示。计算得到的破坏形态与试验结果整体类似，显示出辐射状与环状相叠加的破坏形态。从整体效果来看，本文采用的模型已较好地刻画了炸药试样被撞击后的破坏形貌。当然，炸药试样变形破坏成因复杂，尤其是撞击中心部位(经历过高约束压力等复杂应力状态)，本文提出的模型还不能正确描述，其中的变形破坏机理还需要进一步地认识和研究。

图12 撞击后炸药试件背面的破坏情况Fig.12 Damage in the rear of the explosive specimen after impact

除上述试验结果外，文献[11]中还给出了一组PBX炸药与钢盒接触界面处应力随时间的变化曲线。本文对此工况也进行了计算，计算结果与试验结果对比如图13所示。试验中，PBX炸药发生了起爆，因而应力响应在曲线尾部会有一个突跃，而本文中没有考虑炸药的化学反应，计算结果中没有显现出这一现象。从对比结果来看，数值计算结果的峰值比试验结果要高，应力上升速度快于试验结果，而应力下降速度慢于试验结果。但从应力响应持续时间及应力响应曲线中出现的平台特征来看，本文中的模型也显示出了很好的刻画能力。造成数值计算结果与试验结果差异的可能原因有很多，如界面接触情况等，但由于缺乏更多的试验细节，本文就不再展开分析。

图13 应力时程曲线计算与试验结果的对比Fig.13 Comparison of calculated and experimental stress-time-history curves

4 结论

本文针对复杂应力状态下PBX炸药动态响应描述的问题，在K&C模型的基础上，修改了模型中的损伤演化模式，考虑了材料模量、强度等的压力相关性，计及了材料的应变率效应，给出了材料拉伸、压缩子午线之比的取值，处理了结构在损伤破坏过程中变形局部化的问题，提出了拉伸失效单元的处理方法，最终得到的模型较好地描述了撞击作用下PBX炸药的损伤破坏形貌及力学响应。

在模型的实现过程中，得出以下结论：

1)材料屈服强度随压力呈线性变化时，如果变化的斜率不随应变率发生改变，就相当于采用径向应变率增强的方式来描述材料的应变率效应，二者是等价的；PBX炸药强度随压力的变化并不是简单的线性变化，因而在采用径向应变率增强方式时，需要做出相应的修正。

2)从拉伸、压缩子午线之比的数值来看，在较低约束压力下(压缩情况下)，K&C模型中经验方程给出的数值偏大，在单轴压缩时，拉伸、压缩子午线之比已经达到0.90，显然不合理，需要修正；PBX炸药拉伸、压缩子午线之比随压力的变化还需要进一步的试验研究。

3)在采用有限元方法刻画PBX炸药的变形破坏过程时，需要解决材料变形局部化的问题；数值上解决这个问题的思路主要是抑制计算中不真实的变形局部化的出现，使结构整体响应与试验结果保持一致；由于只在加载方向进行了校准，虽然可以较好地捕捉到试件加载方向的变形情况，但对于其他未校准方向，就不能很好地描述，当然，变形局部化涉及到对空间不连续问题的描述，这需要进一步的研究。

4)在有限元程序中，单元的失效等同于单元的删除，而PBX炸药易于产生拉伸破坏，如果把拉伸破坏简单的处理为单元失效的话，将会不真实地削弱材料的压缩承载能力，在程序实现时，要尽量地减小拉伸失效对压缩过程的影响。