基于三态信号的测试数据相容压缩方法

陈田 左永生 安鑫 任福继

摘 要：针对超大规模集成电路（VLSL）的发展过程中测试数据量增加的问题，提出了一种基于三态信号的测试数据压缩方法。首先，对测试集进行优化预处理操作，即对测试集进行部分输入精简和测试向量重排序操作，在提高测试集中无关位X的比例的同时，使各测试向量之间的相容性提高;随后，对预处理后的测试集进行三态信号编码压缩，即利用三态信号的特性将测试集划分为多个扫描切片，并对扫描切片进行相容编码压缩，考虑多种相容规则使得测试集的压缩率得到提高。实验结果表明，与同类压缩方法相比，所提的方法取得了较高的压缩率，平均测试压缩率达到76.17%，同时测试功耗和面积开销也没有明显增加。

关键词：测试数据压缩;三态信号;相容压缩;扫描切片;自动测试设备

中图分类号： TP391. 7（机器辅助技术）

文献标志码：A

Abstract： Focusing on the increasing amount of test data in the development of Very Large Scale Integration （VLSI）， a test data compression method based on tri-state signal was proposed. Firstly， the test set was optimized and pre-processed by performing partial input reduction and test vector reordering operations， improving the compatibility among test patterns while increasing the proportion of dont-care bit X in the test set. Then， the coding compression of tri-state signal was performed to the pre-processed test set， so that the test set was divided into multiple scan slices by using the characteristics of tri-state signal， and the tri-state signal was used to perform compatible coding compression on the scann slices. With various test rules considered， the test set compression ratio was improved. The experimental results show that， compared with the similar compression methods， the proposed method achieves a higher compression ratio， and the average test compression ratio reaches 76.17% without significant increase of test power and area overhead.

Key words： test data compression; tri-state signal; compatible compression; scan slice; Automatic Test Equipment （ATE）

0 引言

随着超大规模集成电路（Very Large Scale Integration， VLSI）产业的高速发展，集成电路芯片中晶体管的数量在不断地增长，为了确保芯片的故障覆盖率，测试数据量也相应地增加，这对自动测试设备（Automatic Test Equipment， ATE）的存储容量及带宽的大小提出了一定的挑战。更多的测试数据意味着测试时间和测试功耗的增加，而ATE的成本、测试时间和测试数据量等是造成整个测试成本增加的主要因素。

测试数据压缩技术可以有效应对测试数据增加问题[1]。基于编码的压缩方法是测试数据压缩技术中非常重要的一类，可以较好地与设计流程兼容。该方法首先将预计算的测试集编码为更小的数据集，再将压缩后的数据集存储在ATE中，在测试时，压缩集通过ATE和芯片之间的通信通道进入芯片，然后经过芯片上的解压缩结构生成与原始测试数据相容的测试向量。通常，预计算的测试集一般包括0、1和無关位X，称之为测试立方集。而传统压缩方法是将测试立方集编码为以逻辑值0和1表示的编码数据，最开始提出的有哈夫曼编码（Huffman Codes）[2]、FDR码（Frequency-Directed Run-length Codes） [3]等传统编码方法，但该类方法取得的压缩效果并不显著。后来，文献[4]提出通过增加镜像参考向量以提高相容性来对测试集进行压缩;文献[5]提出对测试集进行多次压缩以提高压缩率，但多次压缩导致解压结构面积开销增大。上述这些传统方法仅考虑到二值信号的压缩，然而ATE不仅支持0、1信号的数据传输，同时也支持高阻态信号（Hi-Z）的传输[6]，这就为编码压缩方法提供了一个新思路，对测试立方集以三值逻辑进行编码，并将压缩后包含三态信号的压缩集存储在ATE上。以这样的方式存储的信息，只需要在芯片上利用一个将三态信号转为二值逻辑的结构，再与合适的解压结构结合，就可以实现一种基于三态信号的编码方式。文献[7]提出一种基于字典的三态信号编码方法，但该方法并未考虑到测试向量间的相关性联系，未能针对此方面进行优化。

为了解决传统测试数据压缩方法只能利用二值信号进行编码，同时在已有基于三态信号编码中未能针对测试向量之间关联性作出相应优化等问题，本文提出了一种基于三态信号编码的测试数据相容压缩方法。为了取得良好的压缩效果，该方法考虑测试向量之间的相关性，首先对测试立方集进行预处理操作，利用部分输入精简和测试向量重排序提高测试集的相容性;随后，再使用三态信号编码对测试集进行了三态信号相容压缩，编码时根据测试向量之间关系，结合三态信号可以提高可携带信号量的特性，设计多种相容类型进行编码，在测试功耗及面积开销未有明显增加的情况下，提高了测试数据的压缩率。

1 基于三态信号的编码方法

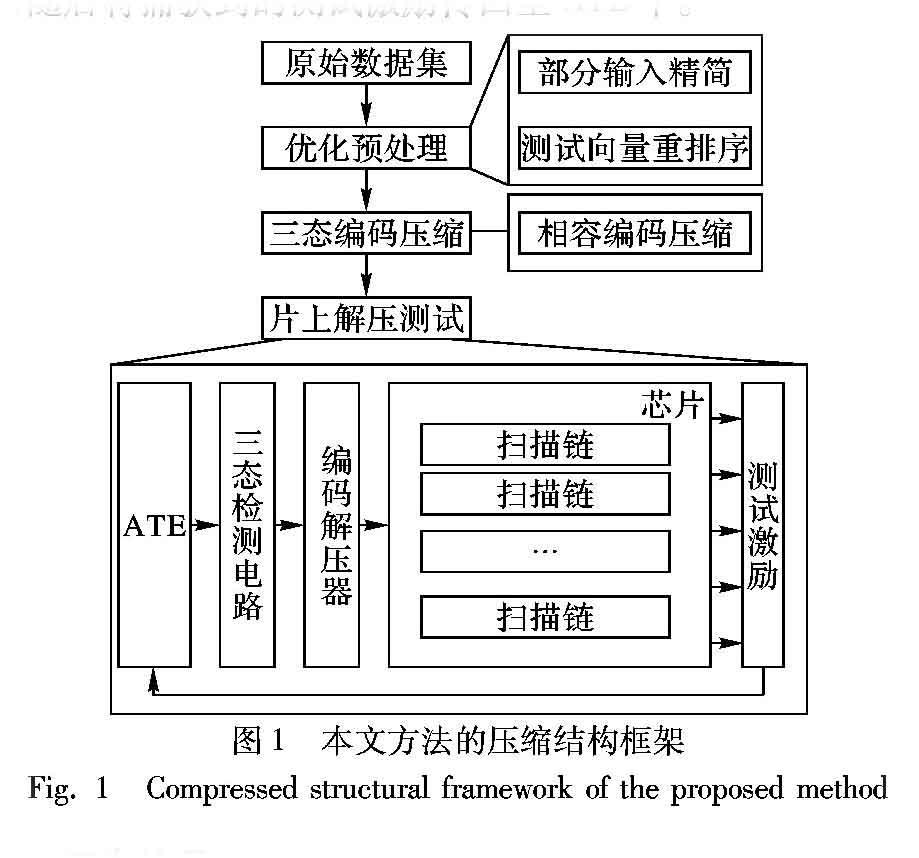
本文方法的压缩结构框架如图1所示。首先，对自动测试向量生成（Automatic Test Pattern Generation， ATPG）产生的原始数据集进行优化预处理操作;然后，对数据集进行三态相容编码压缩;在片上解压测试阶段，在ATE上存储的编码通过一个三态检测电路来进行三态信号和二进制数值的转换，再通过设计的编码解压器对传入到芯片中的数据进行解压测试，随后将捕获到的测试激励传回至ATE中。

1.1 三态信号

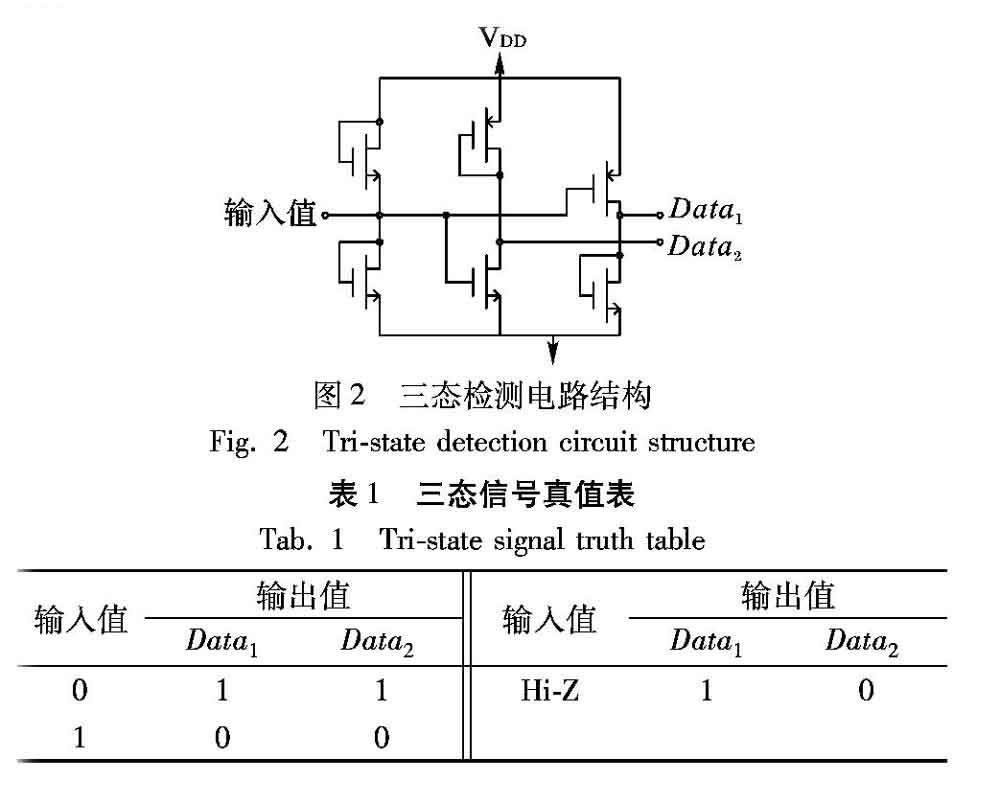
大多数芯片内部的逻辑电路无法识别和处理高阻态信号，但文献[6]中提出ATE可以支持高阻态信号的传输，因此，在基于三态编码的方案中，关键是如何在芯片上检测到三态信号，并将包含三态输入信号的数据重新转换成只包含0、1的测试数据。文献[8]提出了一种三态信号检测电路，但该电路的硬件开销较大，不能应用于本文所提出的方法中。随后，文献[9]提出了另外一种只包含6个晶体管的三态信号检测电路，该三态输入检测电路如图2所示，此电路有一个三态信号输入端口和两个二进制输出端口，可以为三种输入信号状态中的每一种产生唯一的二进制输出;同时，该电路面积开销和复杂性都很小，并且该电路的二进制输出可以很容易地与解压电路的控制模块相结合。故本文选择此三态检测电路用于解压结构中，并结合其他逻辑门将三态信号应用于测试数据的解压缩流程中，表1给出了此三态检测电路的真值表。

1.2 测试集优化预处理

通过ATPG得到的确定测试集中通常含有大量无关位X，对这些测试向量进行相容性压缩，将在一定程度上减少测试数据量[10]。而测试集中的无关位X的比例越高，测试集中的相邻测试向量的相容性就越高，这就为测试数据压缩前的预处理提供了理论依据。在本文采取的优化预处理步骤中，共分为部分输入精简操作和测试向量重排序操作两部分。

由于本文采用相容压缩方法，测试集中无关位X的比例越高，后续压缩处理和功耗处理取得的效果越好，故本文采用输入精简方法对测试集进行优化。传统输入精简[11]是一种通过检测被测电路相容或反向相容输入并对其进行合并处理的方法。该方法虽然可以压缩测试集，但存在着如下问题：该方法在对测试集进行合并处理时会造成电路布线难度呈线性提高，同时测试功耗也会相应地提高。考虑到上述问题，本文决定采用部分输入精简方法有选择性地利用电路相容和反向相容，尽可能地提高电路无关位X位的比例，使之有利于三态信号相容压缩，同时布线难度和功耗没有大幅度提升。如图3所示，使用传统输入精简可以将6条扫描切片压缩至1 条;而综合考虑布线难度和功耗的部分输入精简方法有选择性地选择第1、2和6条扫描切片，将扫描切片压缩至3条，此时无关位X的比例从50%上升至58%。

根据本文编码规则，相邻测试向量之间的海明距离越小，它们之间可相容的概率就越高，压缩处理的效果就越好。为了使测试集的相邻测试向量可以有更高的相容性，本文使用测试向量重排序方法来进行优化。本文提出的方法是通过调整各条测试向量的位置来寻找最优相邻测试向量排序，使得调整后的相邻测试向量间的总海明距离最短，这样可以最大限度提高各条相邻测试向量之间的相容性。求解该最优测试向量排序问题可以抽象为一个旅行商问题（Travelling Salesman Problem， TSP），通过启发式算法能在可接受的范围内求得相对最优解。该排序问题的具体模型如下：将测试集中每个测试向量看作是图的一个端点，测试向量之间的海明距离看作是端点之间的权值，可以通过这些权值构建一个邻接矩阵;图中路径的含义是各条测试向量的排列顺序，路径距离的含义是测试向量跳变时的海明距离，路径的选择目标是得到所有路径之中的跳变最小值，通过计算得出的路径可以获得一个近似最优的测试集。由于构建的模型数据量较大，而遗传算法（Genetic Algorithm， GA）具有较强的全局搜索能力，所需计算时间较少，故本文选用遗传算法（GA）作为求解该问题的方法。

1.3 测试数据相容压缩方法

1.3.1 基本扫描切片相容类型

根据测试数据相容压缩方法思想，本文设置一个参考扫描切片作为基准向量，通过扫描切片与参考扫描切片相容时的不同相容关系来对测试集进行基于三态信号的编码。扫描切片相容是指相邻扫描切片之间满足相容性關系。对于任意两条N位的扫描切片xi：（x1，x2，…，xN）和yi：（y1，y2，…，yN），当xi与yi的值相同或者它们中至少有一个是无关位X时，则称这两条扫描切片正向相容;当xi与yi的值完全相反或者它们中至少有一个是无关位X时，则称这两条扫描切片反向相容;同时，测试向量划分为更小的扫描切片后，有大量的只包含无关位X和1/0的扫描切片或者全为无关位X的扫描切片，将这些切片划分为全零或全一相容扫描切片。

1.3.2 特殊扫描切片相容类型

在上述测试集优化预处理过程中，发现许多扫描切片之间的海明距离实际上很小。如在扫描切片的长度为8位的情况下，不相容的两个扫描切片之间海明距离的均值在1～2。在上述基础上，对选用扫描切片间一位或者两位不同作为一个扫描切片相容的类型给出数学上的理论分析。对于两个给定长度N位的任意扫描切片A和任意扫描切片B，假设0、1、X的概率分别为P0、P1和PX。

1.3.3 三态编码表编码规则

根据上述扫描切片相容类型，基于哈夫曼编码原理，本文对扫描切片与参考切片各种相容类型情况的出现频率进行统计，构造出基于三态电路的测试数据相容压缩编码方法。如表2所示，对于长度为N的扫描切片，当扫描切片与参考切片为全零或全一扫描切片时，选择“0”或“Z0”作为编码值;当扫描切片与参考切片完全不相同时，选择“1”加原始扫描N位扫描切片作为编码值;当扫描切片与参考切片全相容或者反向相容时，选择“ZZ0”或“ZZ1”作为编码值;对于上述一位不同特殊情况时，选择“Z1”和一位不同位置的编码作为编码值。

1.3.4 三态编码表编码流程

设置Si表示当前扫描切片，Ri表示参考切片，假设每个扫描切片的位数为8位，Ci为编码结果，本文的基于三态信号测试数据相容压缩编码过程如下：

1）初始化参考向量R0为“00000000”。

2）将当前向量Si与全零、全一进行相容比对，如果与全零、全一相容，则将参考切片改为相应的全零、全一切片，编码结果为0或Z0;如果与全零、全一不相容，则转至步骤3）。

3）将当前参考向量Ri与当前向量Si进行相容比对，如果为不相容则转至步骤4）;如果为相容，则编码结果为ZZ0，并且参考向量Ri+1=Ri&Si;如果为“反向相容”，则编码结果为ZZ1，同时参考向量Ri+1=（～Ri） & Si;如果为一位不同，则编码结果为Z1加上那一位不同的位数的二进制编码，同时参考向量Ri+1 不变。

4）当相容比对的结果为不相容时，编码结果为1加Si的值 ，同时参考向量Ri+1=Si。

本文以表3作为示例介绍编码的过程。编码开始，参考切片初始化为00000000，扫描切片S1=0XXXX1X1，参考切片R1为00000000，扫描切片与参考切片不相容，将参考切片R2更新为S1，同时编码结果C1为100000101;随后，扫描切片S2=XXX1XXX1，为全一扫描切片，故编码为Z0，同时将参考切片R3更新为S2;随后，扫描切片S3=XX00XXXX，为全零扫描切片，故编码为0，同时将参考切片R4更新为S3;随后，S4=1XX11X00，与参考切片R4相比为不相容，故将参考切片R5更新为S4，同时编码为110011000;随后，S5=1XX110XX，与参考切片R5全相容，故参考切片R5不变，同时编码为ZZ0;随后，S6=00XX1X0X，与参考切片R6相比为一位不同的状态，故参考切片R6不变，同时编码为Z1000;随后，S7=0X1X0XX1，与参考切片R7相比为反向相容的状态，故将参考切片更新为S7，同时编码为ZZ1;最后，S8=011XX101，与参考切片R8相比为一位不同的状态，故编码为Z1110。从表3例子可以看出，未编码之前测试集的位数为64位，编码之后的位数为37位，测试数据得到了压缩，同时只有两个不相容的情况需要串行加载，其余的则可以并行加載。

2 解压结构

本文方法的解压结构如图6所示，三态检测电路将输入数据转换为二进制数据传入到有限状态机（Finite State Machine， FSM）中，FSM用于测试向量相容压缩解码信号控制。信号处理模块为对从FSM中传出的控制信号和数据进行处理。假设被测电路含有N条扫描链，其中参考切片存储在一个N位的移位寄存器RS1中，一位不同位存储在一个lb N位的移位寄存器RS2中。当扫描切片与参考切片相容时，把对应的参考切片移入扫描链中;当扫描切片与参考切片不相容时，先将扫描切片移入到参考切片中，随后将替换后的参考切片移入扫描链中;当扫描切片与参考切片一位不同时，选择相应一位不同位进行翻转，并将翻转后的参考切片移入扫描链中;当扫描切片为全一、全零状态时，将参考切片完全填充为全一或全零，再将参考切片移入扫描链中。

具体的解压过程如下：1）当解压器使能信号“en”为“1”时，“Data_In”端口开始接收数据，通过三态检测电路得到只包含二进制的数据，将其传入FSM中。2）当扫描切片与参考切片不相容时，参考切片需要更换，此时计数器CountA中有两个信号“dec_A”和“shift”，当“dec_A”信号为“1”，“shift”信号为“1”，“se”的信号为“0”，K位计数器A开始计数，“Data_RS”端口开始将输入数据移入移位寄存器RS1中。当计数到N个周期时，“rs_A”的信号将被置为“0”，“dec_a”“shift”“se”的信号值翻转。此时，一个扫描切片的输入数据已经完全移入至参考切片中，同时被测电路的相应数据也已经移入扫描链中。3）如果扫描切片与参考切片完全相容时，则“xor”信号为“1”;反向相容时，“xor”信号为“0”。计数器CountB中有两个信号“dec_B”和“shift”信号，如果扫描切片与参考切片一位不同时，“od_shift”信号为“1”，“dec_B”信号为“1”，CountB开始计数，“Data_RS”端口开始将输入数据移入移位寄存器RS2中。当计数到lb N个周期时，“rs_B”的信号将被置为“0”，“od_shift”“dec_B”信号值翻转，同时将“One_Dif”信号值变为“1”，“se”信号为“0”，通过译码器进行一位不同位的选择，同时将被测电路的相应数据移入扫描链中。4）当扫描切片为全零、全一时，“C_Z/O”端口输出信号为“1”，同时“dec_A”信号为“1”，“shift”信号为“1”，“se”的信号为“0”，K位计数器A开始计数，此时“Z/O”端口输出“0”或“1”代表全零、全一，将输入数据移入RS1中。当计数到N个周期时，“rs_A”的信号将被置为“0”，“dec”“shift”“se”的信号值翻转。此时，一个扫描切片的输入数据已经完全移入至参考切片中，同时被测电路的相应数据也通过控制和状态寄存器 （Control and Status Register， CSR）已经移入扫描链中。

3 实验与结果分析

为了验证本文方法的有效性，本文针对ISCAS-89中的基准电路进行实验，采用Mintest集作为确定测试集。测试压缩程序在Core i5-3470 3.2GHz CPU、8GB内存PC上使用C++程序设计语言进行实现并解压。实验电路的基本信息如表4所示。

从表5可以看出，与已有二值信号压缩方法相比，本文方法的压缩率普遍优于已有二值信号的压缩方法;与三态信号压缩方法相比，本文方法除s13207电路压缩率略低于该方法外，其他电路压缩率明显优于该方法。同时表5中还给出了本文方法优化操作前后对比，可以看出，经过优化预处理操作后的测试集的压缩率明显优于未经优化的测试集。本文方法能够取得较高压缩率的原因在于：在压缩前先将测试集进行预处理，提高了测试集中测试向量无关位X的比例，同时经过测试向量重排序后的测试集也更有利于相容编码压缩;在随后进行三态信号编码时，不仅考虑测试向量直接相容的情况，还考虑了反向相容及一位不同相容的情况，从而提升了压缩率。

文献[16]提出了用于度量测试功耗中移位功耗的近似模型，这一方法称为加权翻转度量（Weighted Transition Metric， WTM），该方法可以广泛地用于估计基于串行扫描结构的测试中的功耗。该方法对翻转的加权值是根据翻转在测试模式的位置得到。测试向量移入的功耗WTMi为：

不同方法的面积开销对比如表7所示。本文利用Synopsys公司的DC（Design Compiler）工具对解压结构以及相对应的基准电路进行了综合和分析，面积开销计算式为：解压结构面积/基准电路面积*100%。本文方法虽然使用了三态检测电路，但是它只由六个晶体管组成，面积开销较小，其余的电路开销为控制电路的开销。

由表7可以看出，与Golomb码、FDR码等传统二值信号压缩方法的硬件开销相比，本文方法的电路开销略有增加，解码电路的面积开销大约在MDPRC码和文献[5]方法之间;与文献[7]的三态信号压缩方法相比，本文方法的面积开销也没有明显的增加，最多仅高出2.6个百分点左右，在可接受范围内。

4 结语

针对测试数据量增加的问题，本文提出了基于三态信号测试数据的相容压缩方法。该方法首先对测试集进行预处理，通过进行部分输入精简操作和测试向量重排序，在提高测试集中无关位X数量的同时提高了测试向量之间的相容性;然后，对预处理后的测试集进行三态相容编码压缩，在编码时通过设置一个参考切片作为参考量，考虑了多种情况下的相容类型，并且考虑到一位不同特殊情况下的相容情况，得到了较高的测试数据压缩率;最后，设计了压缩方法在片上的解压结构。实验结果表明，在没有过高的面积开销和测试功耗的情况下，与其他已有压缩方法相比，本文方法取得了较高的压缩率。

参考文献 （References）

[1] MIRTHULLA S， ARULMURUGAN A. Improvement of test data compression using combined encoding [C]// ICECS 2015： Proceedings of the 2015 2nd International Conference on Electronics and Communication Systems. Piscataway， NJ： IEEE， 2015： 635-638.

[2] GONCIARI P T， AL-HASHIMI B M， NICOLICI N. Variable-length input Huffman coding for system-on-a-chip test [J]. IEEE Transitions on Computer-Aided Design of Integrated Circuits and Systems， 2003， 22（6）： 783-796.

[3] CHANDRA A， CHAKRABARTY K. Test data compression and test resource partitioning for system-on-a-chip using Frequency-Directed Run-length （FDR） codes [J]. IEEE Transactions on Computers， 2003， 52（8）： 1076-1088.

[4] 鄺继顺，刘杰镗，张亮.基于镜像对称参考切片的多扫描链测试数据压缩方法[J].电子与信息学报，2015，37（6）：1513-1519.（KUANG J S， LIU J T， ZHANG L. Test data compression method for multiple scan chain based on mirror-symmetrical reference slices [J]. Journal of Electronics & Information Technology， 2015， 37（6）： 1513-1519.）

[5] 陈田，易鑫，王伟，等.一种低功耗双重测试数据压缩方案[J].电子学报，2017，45（6）：1382-1388.（CHEN T， YI X， WANG W， et al. Low power multistage test data compression scheme [J]. Acta Electronica Sinica， 2017， 45（6）： 1382-1388.）

[6] SEO S， LEE Y， KANG S. Tri-state coding using reconfiguration of twisted ring counter for test data compression [J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems， 2016， 35（2）： 274-284.

[7] CHEN T， LIN C X， LIANG H G， et al. A dictionary-based test data compression method using tri-state coding [C]// ATS 2018： Proceedings of the 2018 IEEE 27th Asian Test Symposium. Piscataway， NJ： IEEE， 2018： 42-47.

[8] NICOLAI J. Integrated circuit with mode detection pin for tristate level detection： U.S. Patent 5198707 [P]. 1993-05-30.

[9] THOMSON D， SHERIDAN P， CLEARY J. Tri-state input detection circuit： U.S. Patent 6133753 [P]. 2000-10-17.

[10] GONCIARI P T， AL-HASHIMI B M， NICOLICI N. Variable-length input Huffman coding for system-on-a-chip test [J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems， 2003， 22（6）： 783-796.

[11] CHEN C A， GUPTA S K. Efficient BIST TPG design and test set compaction via input reduction [J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems， 1998， 17（8）： 692-705.

[12] BUTLER K M， SAXENA J， FRYARS T， et al. Minimizing power consumption in scan testing： pattern generation and DFT techniques [C]// ICT 04： Proceedings of the 2004 International Conference on Test. Washington， DC： IEEE Computer Society， 2004： 355-364.

[13] CHANDRA A， CHAKRABARTY K. System-on-a-chip test-data compression and decompression architectures based on Golomb codes [J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems， 2001， 20（3）： 335-368.

[14] EL-MALEH A H. Test data compression for system-on-a-chip using extended frequency-directed run-length code [J]. IET Computer and Digital Techniques， 2008， 2（3）： 155-163.

[15] TSENG W D， LEE L J. Test data compression using multi-dimensional pattern run-length codes [J]. Journal of Electronic Testing： Theory and Applications， 2010， 26（3）： 393-400.

[16] SANKARALINGAM R， ORUGANTI R R， TOUBA N A. Static compaction techniques to control scan vector power dissipation [C]// VTS 2000： Proceedings of the 2000 18th IEEE VLSI Test Symposium. Washington， DC： IEEE Computer Society， 2000： 35-40

[17] BHAVSAR K A， MEHTA U S. Analysis of dont care bit filling techniques for optimization of compression and scan power [J]. International Journal of Computer Applications， 2011， 18（3）： 30-34.