冲击荷载作用下埋地长输管道受力性能分析

董飞飞，曾磊，谢向东，杜国锋

(长江大学城市建设学院， 湖北荆州434000)

0 引言

长输油气管道埋设在丘陵、山地、滑坡等复杂地表环境下时不可避免地会遭受落石冲击作用。近年来，国内外部分学者展开了对埋地石油管道的研究，主要从理论分析和数值模拟两个方面进行，其中在理论分析方面，顾安全[1]进行了室内模型试验，建立了土压力计算公式，研究了影响管道沉降差的土体因素，但由于土体离散性较大，理论求解比较复杂。王洪波等[2]从理论基础角度推导了管道受冲击荷载的理论应变，总结出管道最大应变计算公式，并提出管道环向应力的临界值计算方法，但其理论推导公式与实际工况下的一些参数选取有所不同，因此计算结果偏保守。在数值模拟方面，刘爱文[3]首先采用壳模型模拟了管道在地震作用下的反应，结果表明，壳模型能很好地分析管道的局部屈曲和大变形问题。国外学者Chiou等[4]利用压缩性软土的本构参数，建立有限元模型并进行数值模拟，重点分析了管径与管壁厚之比、初始缺陷、埋设深度、摩擦参数、土体性质等因素。荆宏远[5]主要从理论计算和数值模拟的角度分析了落石冲击埋地管道的动力响应，结果表明，最大冲击力与速度存在近似正比的关系；在埋地管道的上部土体受到冲击荷载作用时，管道受到土体传递下来的冲击力，导致管道上下表面存在应力集中，并且沿管道纵向、横向分布的竖向应力逐渐向两端衰减。其后，邢义锋、赵师平、丁凤凤等[6-8]从数值模拟的角度分析了埋地管道受落石冲击力的动力响应，建立了落锤—土体—管道三者的模型，重点研究了冲击力、管壁厚、管道与落锤位置的影响因素，但缺乏管道在实际工况条件下的实验论证。

由此可见，研究埋地管道在冲击荷载作用下的力学性能由于管道与土体复杂的非线性接触问题，单从理论求解是比较困难，进行全尺寸的埋地管道冲击试验也存在很多困难，故本研究从试验测试和数值模拟两方面进行研究，主要分析了管道壁厚、管径、埋深和冲击能量等参数对管道动力响应的影响，探讨了冲击荷载作用下埋地管道的应变发展过程和分布规律，总结中提出的相关结论可为管道工程设计和施工提供参考。

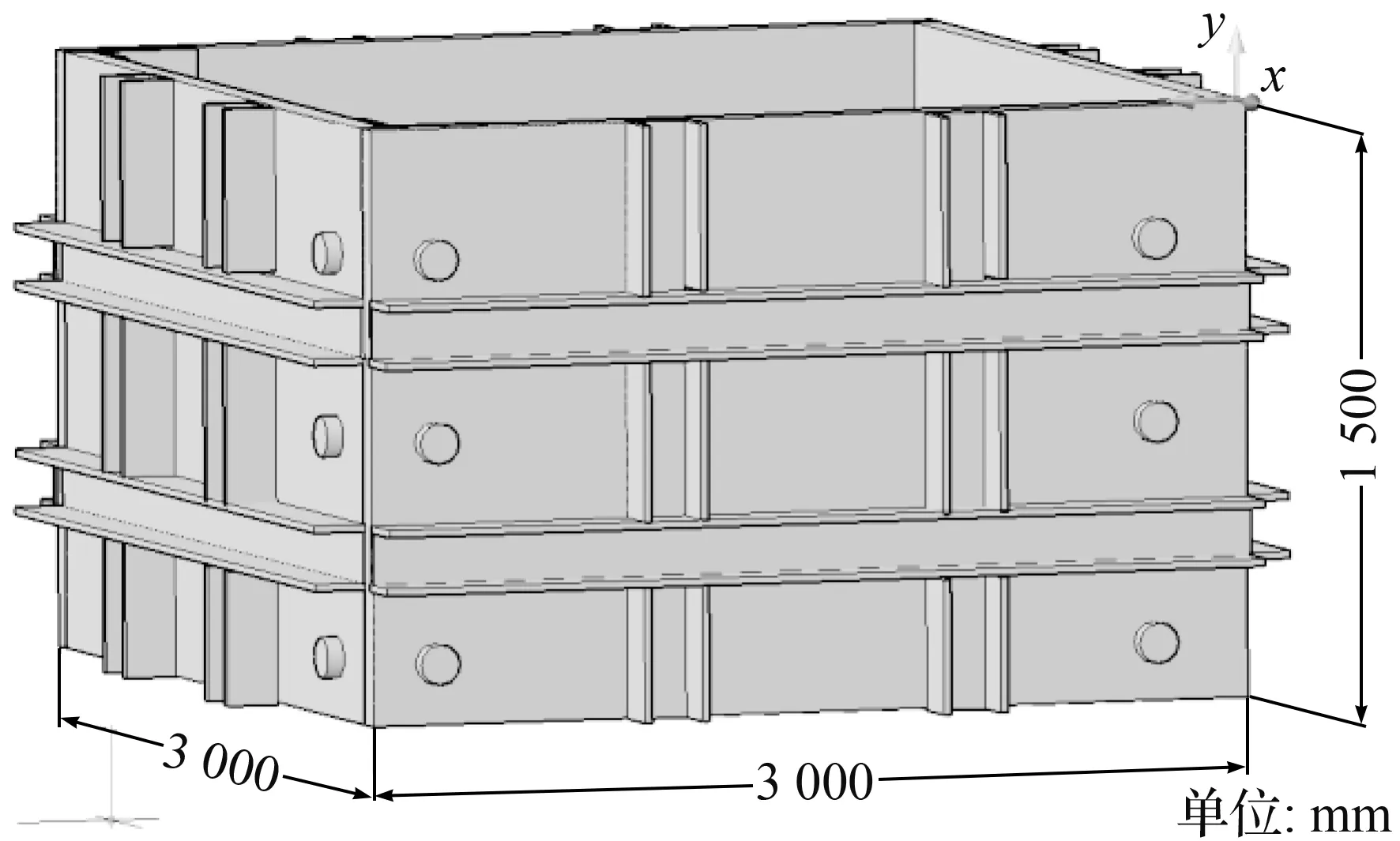
图1 土箱示意图Fig.1 Schematic diagram of soil box

1 试验概况

1.1 试件设计

本次实验的目的为对埋地管道进行落锤冲击荷载试验，探讨了埋地管道在冲击荷载作用下的应变分布规律，并分析了管道壁厚、管径、埋深和冲击能量等参数对管道受力性能的影响。根据我国长输油气管道常用管径的选用规范，在实际工程中管道埋深一般为2.5 m，管径为700 mm，落石冲击埋地长输管道的影响范围一般取20 m，因此本次实验根据参考文献[9-10]和油气输送管道线路工程抗震技术规范[11]，以及实际条件下管道尺寸和埋深，确定相较合理的似比为7∶1，设计出缩尺比例模型如图1所示，故通过缩尺比例，将实际工况下管道的长输距离可简化到2.8 m，采用镀锌钢管，材料为Q235级钢，并设计了不同的管道外径和壁厚有：89 mm×2.5 mm、114 mm×2.5 mm、139 mm×2.5 mm、114 mm×3.0 mm和114 mm×3.5 mm五种；埋深为0.3 m、0.6 m和0.9 m三种，土体尺寸为3 000 mm×3 000 mm×1 500 mm (长×宽×高)，由钢板、槽钢及角钢焊接而成的土箱。具体试验工况如表1所示，其中试验按照不同的工况条件设置了管道试件SG-1、SG-2、SG-3、SG-4、SG-5、SG-6和SG-7七种。

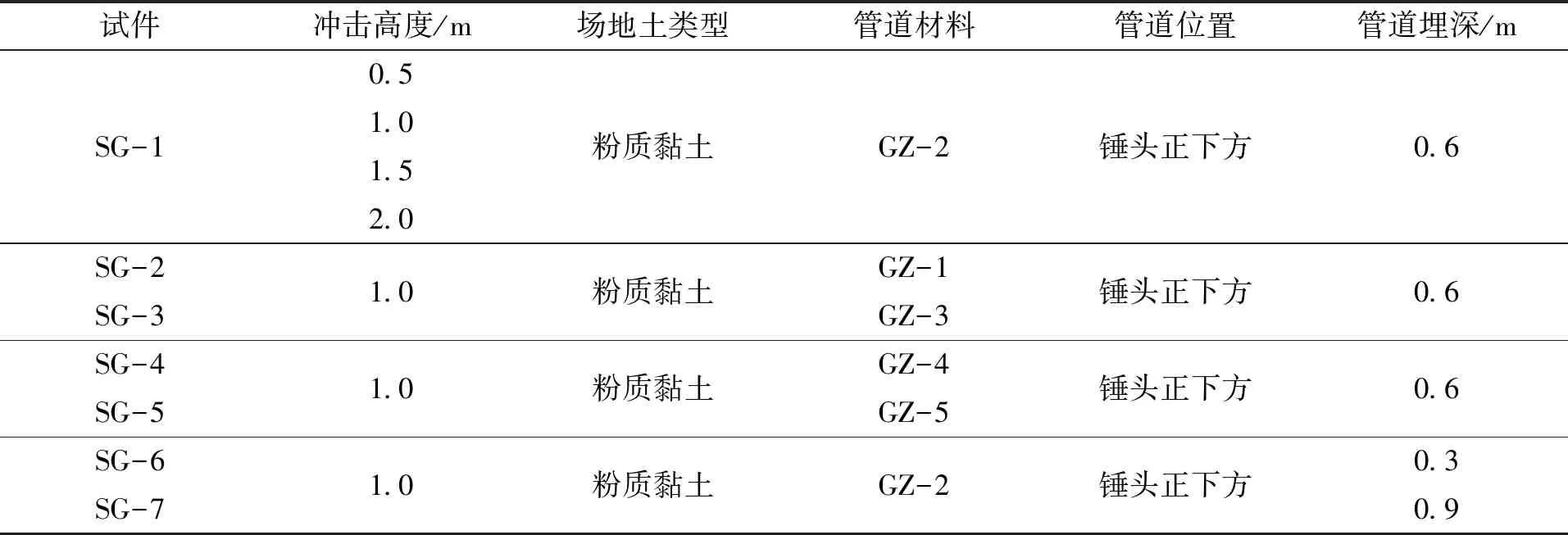
表1 试验工况Tab.1 Experimental conditions

1.2 材料性能

本试验中土体材料采用实际工程中常见的粉质黏土，通过采样压实原土，测得土体的材料参数如表2所示。对管材进行拉伸试验，测得力学性能参数见表3。

表2 土体力学性能Tab.2 Mechanical properties of soil

表3 管材力学性能Tab.3 Mechanical properties of pipeline

1.3 试验加载

本次利用落锤冲击试验机模拟冲击荷载，分别如图2和图3所示。试验机由主体结构、导向柱、落锤、提升装置及控制系统等部分组成。试验机的基本技术指标有：锤头质量339 kg，最大冲击高度7.8 m，最大冲击能量52 kJ。土箱由钢板围合形成，安装在落锤试验机下部，土体装入土箱时分层(每层厚度100 mm)夯实，试验加载前先进行预加载，检验试验装置和测量系统后正式加载，试验中测试管道埋设在锤头正下方区域，以锤头为中点，两端对称分布填埋，如图2所示。落锤冲击高度从0.5 m到2.0 m每隔0.5 m进行一次冲击实验，每下落一次记录一次管道应变，具体工况见表1。

图2 落锤冲击机示意图
Fig.2 Schematic diagram of drophammer impact machine

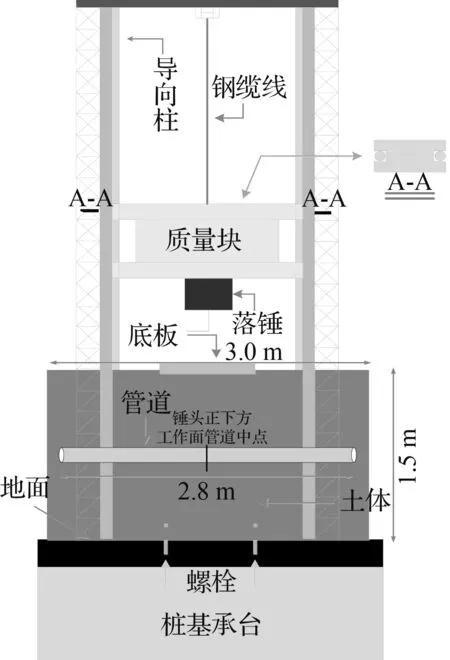
图3 落锤冲击机平面图
Fig.3 Plan for drop hammerimpact machine

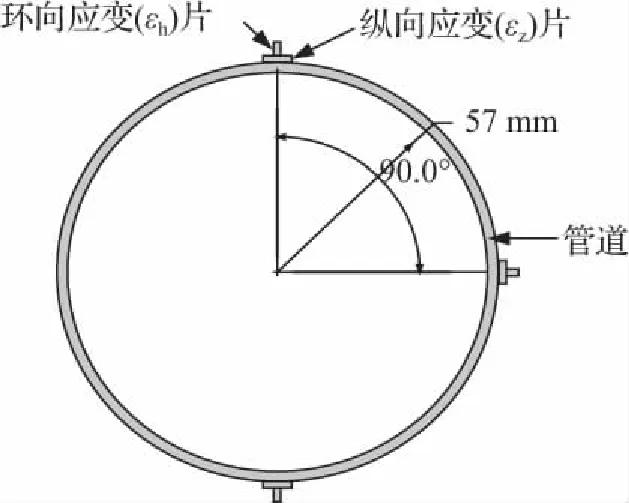
图4 管道截面图Fig.4 Cross section of pipeline

1.4 测点布置

埋地管道受到冲击荷载作用产生的应变可分为纵向应变和环向应变，为测量埋地管道的应变变化过程，应变片采用箔式应变片(2 mm×1 mm)，管道应变片布置如图4和图5所示，沿管道环向分布的应变片为上、下两个面和中部90°面，沿管道轴向分布的应变片以管道中部为中心对称分布，间距700 mm。本试验采用DH5908无线动态应变采集仪记录管道应变片输出的信号，如图6所示。

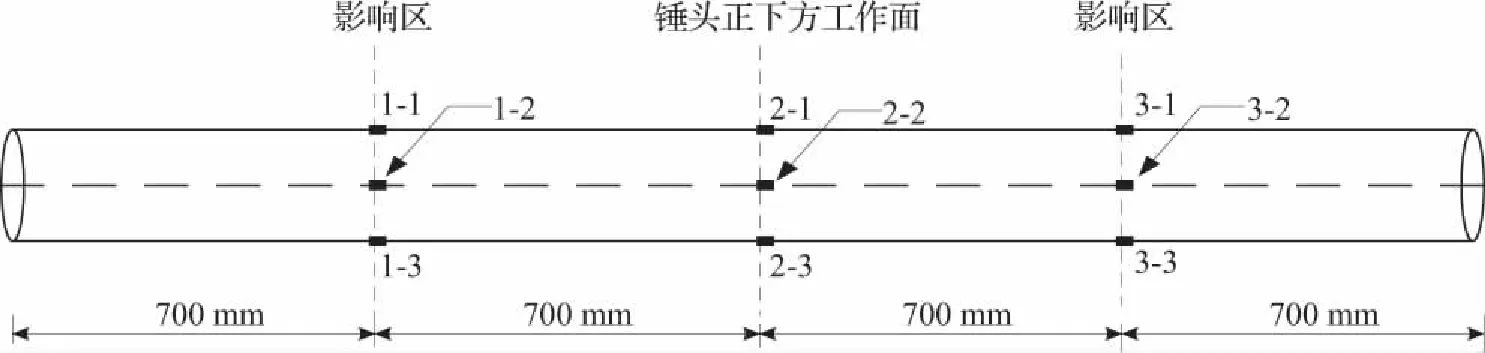
(a) 管道应变测点平面图

(b) 管道应变测点照片

图6 应变采集设备Fig.6 Strain collection equipment

2 试验结果及分析

通过试验测定的管道应变峰值数据如表4。

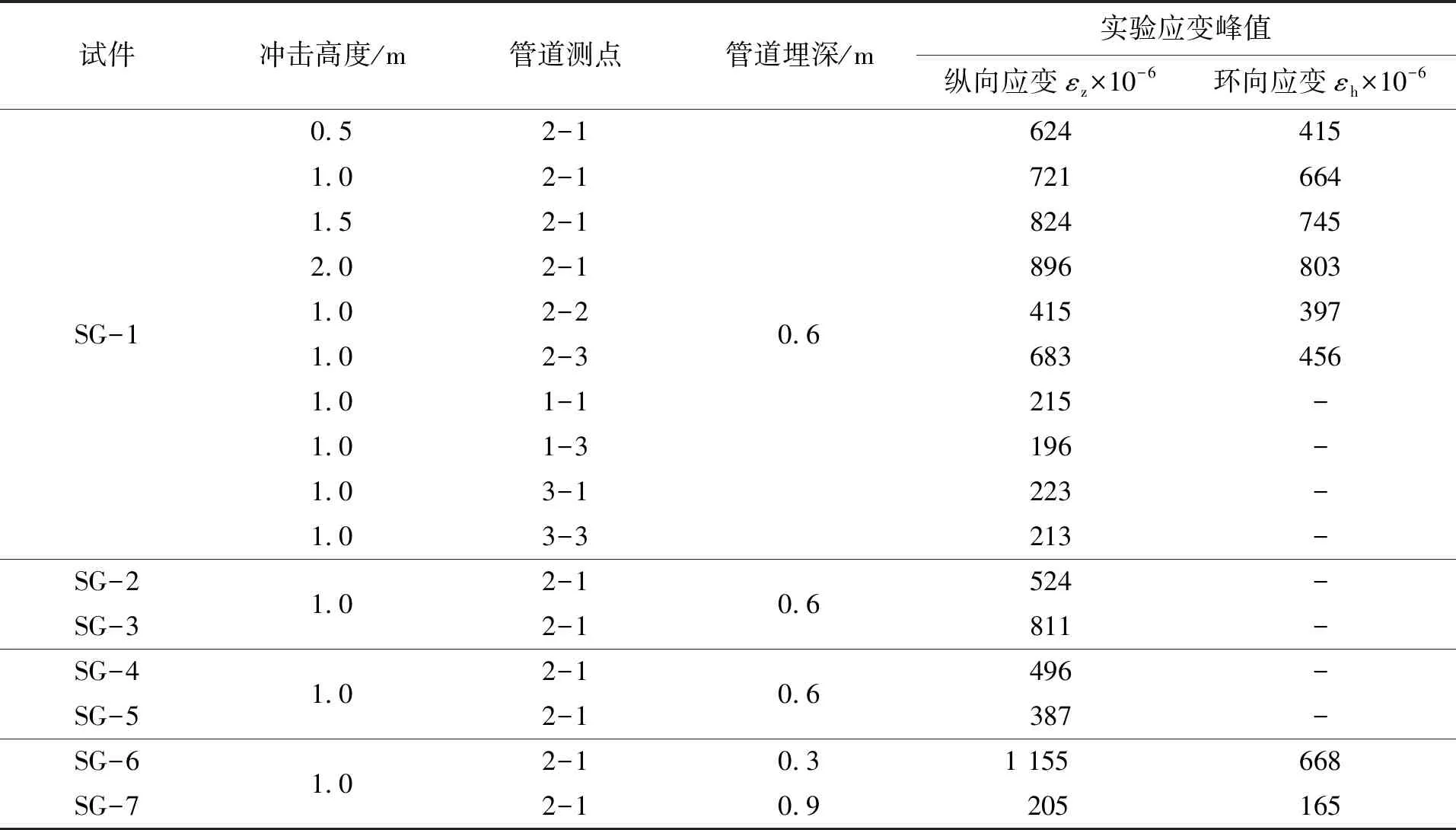
表4 试验试件应变数据Tab.4 Strain data of test specimens

2.1 落锤冲击能量的影响

根据表4中的试验数据结果和图5(a)中管道应变片的不同测点平面图，绘制了图7～图9管道试件SG-1的峰值应变图，其中图7和图8为冲击高度h分别为0.5 m、1.0 m、1.5 m和2.0 m下管道测点2-1和2-3的应变情况，可以看出，随着冲击高度的增加，管道峰值应变也增加，且管道上下表面应变呈现反对称，上表面受压，下表面受拉。在图9中，分析了在落锤冲击高度1 m情况下，管道的纵向应变和环向应变的规律，εZ和εH分别为管道不同测点2-1、2-2和2-3处的纵向应变和环向应变。可以看出，在竖向冲击荷载下，管道主要产生纵向应变和环向应变，且纵向应变最明显，管道在纵向方向应变峰值较大。在管道环向一周截面上，管道上下两面都受压，管道截面90°处受拉，管道中部截面呈椭圆形，符合管道截面环向受力变化规律。由图10可以看得出，在冲击过程中，管道中部应变最大，逐渐向两端减弱，且沿管道两端方向应变具有对称规律。

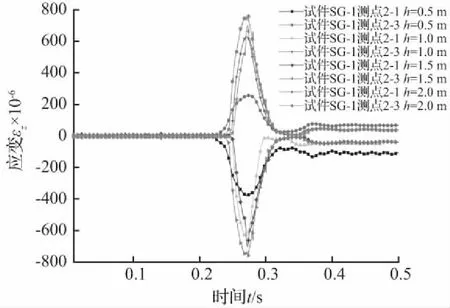
图7 不同冲击高度管道2-1和2-3测点纵向应变
Fig.7 Longitudinal strain of 2-1 and 2-3 measuringpoints of different impact heights

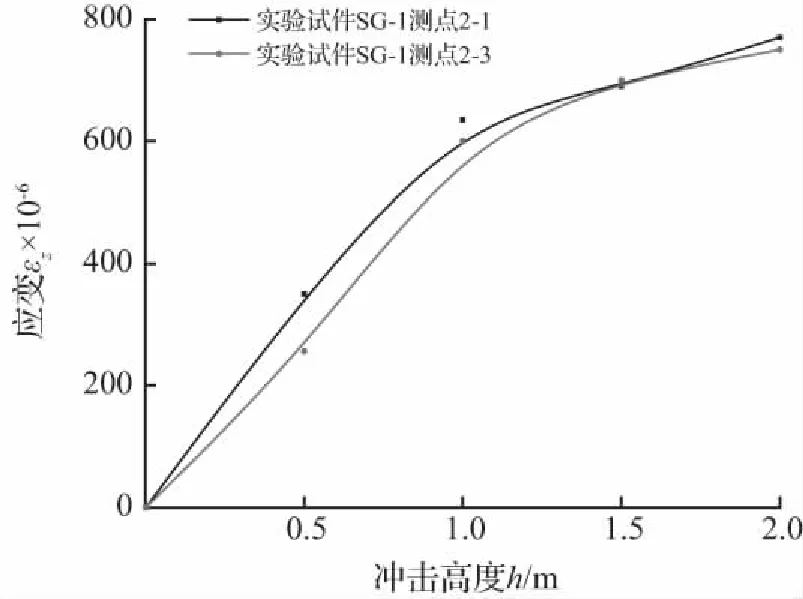
图8 管道2-1和2-3测点纵向应变与不同冲击高度的关系
Fig.8 Relationship between longitudinal strainof pipeline 2-1 and 2-3 measuring points anddifferent impact heights

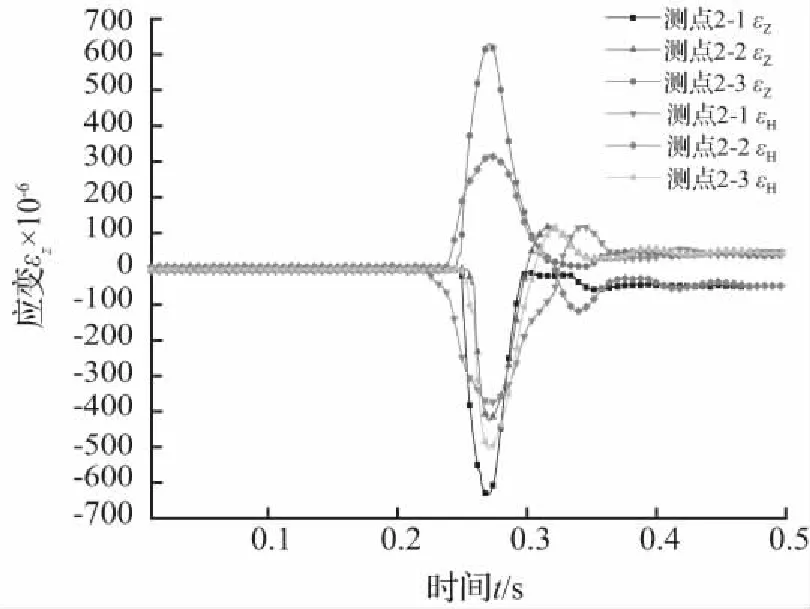
图9 管道2-1、2-2和2-3测点纵向、环向应变
Fig.9 Longitudinal and circumferential strain of2-1, 2-2 and 2-3 measuring points

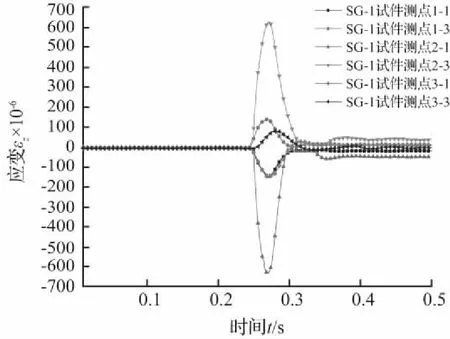
图10 沿管道轴向观测界面各测点纵向应变
Fig.10 Longitudinal strain of measuring pointsalong the pipeline axial observation positions

2.2 管径大小和管壁厚度的影响

根据试验构件SG-1、SG-2、SG-3、SG-4和SG-5的试验数据结果绘制了三种不同管径和不同壁厚的管道应变图，分别如图11和图12所示。从图11可以看出，在冲击荷载作用下，管道管径越大产生的峰值应变越大，主要由于管道管径增大，管道径向刚度变小，且管道在受到土体传递下的竖向荷载作用下时沿管道径向弯曲，因此管径越大，管道峰值应变越大。从图12可以看出，从管道的上下表面应变规律可以看出，管道壁厚越大，管道应变越小，主要由于管道壁厚增加，管道整体刚度变大，随之管道的应变有所减小。

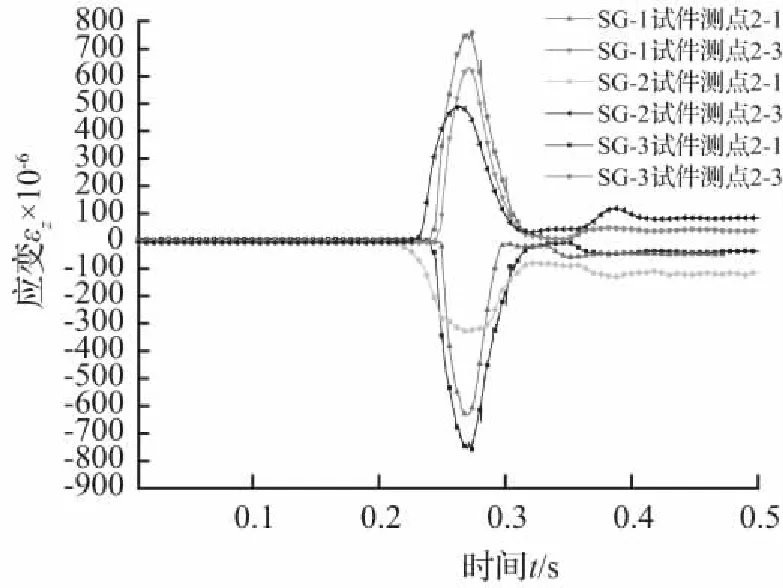
图11 不同管径管道应变
Fig.11 Strain of pipes with different diameters

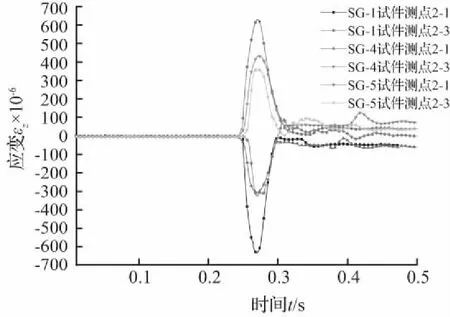
图12 不同壁厚管道应变
Fig.12 Strain of pipes with different wall thickness

2.3 管道埋设深度的影响

设置了管道埋设在0.3 m、0.6 m和0.9 m三种不同深度，图13-14为不同埋深下管道应变情况，从图13和图14中可以看到，管道在冲击荷载作用下，土体起到了缓冲的作用，管道埋设越深，其应变越小，土体分散了落锤的冲击能量。图15为沿管轴方向管道1/4处应变情况，对比图10也可以看出，在埋深相同的基础上，冲击能量沿管道水平传播方向上也逐渐减弱。根据表4中数据结果可知，在冲击荷载作用下管道中部测点2-1处应变最大为1 155×10-6，对比表3中管道材料力学性能可知，管道应力应变处于弹性范围内，未发生屈服。

图13 不同埋深管道应变
Fig.13 Strain of pipes with differentburied depths

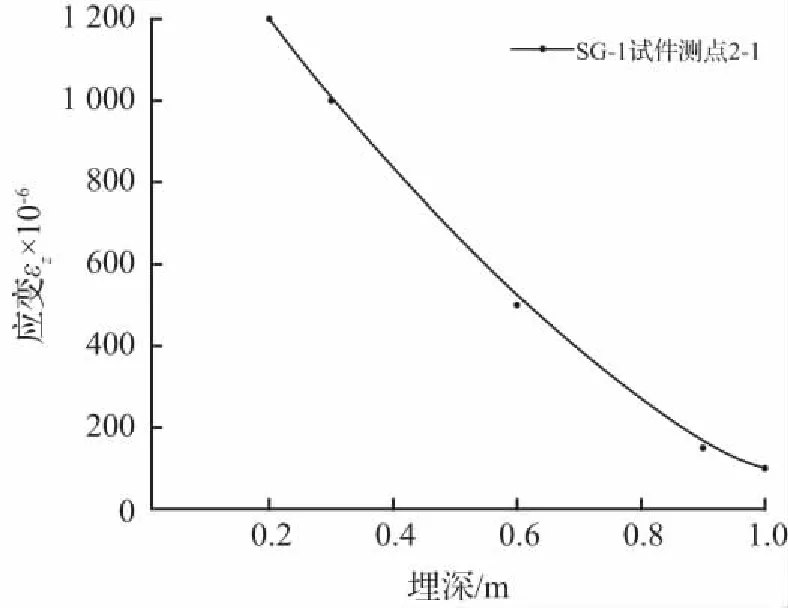
图14 管道应变与埋深关系
Fig.14 Relationship between peak strainand depth of pipeline

3 有限元分析

3.1 土体—管道模型建立

通过大型数值模拟软件ABAQUS完成了土箱—管道的缩尺组合模型，并分析埋地管道在冲击力下的动力响应。有限元计算模型分为四个部件，分别为土体、管道、落锤和刚性垫块。在ABAUQS模型中，土体材料采用的是Mohr-Coulomb[12]模型，没有考虑土体的剪胀角，土体种类如表1所示。管道材料根据《油气输送管道线路工程抗震设计规范(GB 50470—2008)》所应用的管道钢三折线模型，考虑了对于管道大应变的问题，管道设计工程常用三折线模型，具体参数如表3所示。由于冲击过程中，锤头变形较小，且锤头的应变变化不是本文研究重点，故将锤头设置为刚性材料。根据参考文献[13-14]管道选取4节点的壳单元，土体选取8节点的均匀实体单元，土体、管道各部件网格划分如图16所示，考虑了管道与土体接触的非线性问题，故接触界面算法采用了接触力的罚函数算法，且管道与土体之间的接触类型为双向自动接触类型，分别定义了管道与土体的主从接触面，这种接触面通过有限元中壳—实体耦合[15]约束来完成，相互耦合约束作用分为法向作用和切向作用，其中切向作用考虑了管土之间的相对滑移，采用库伦摩擦模型来传递管—土表面的剪应力，库伦摩擦系数设定为0.8[14]。在管道与土体的边界条件的设定中参考相关文献[16-18]，土体地表面不施加任何约束，为自由面，且落锤与土体的接触为自动面接触；土体四周和下部约束为固定约束，其边界为固定边界。在施加荷载过程中，将落锤模拟成自由落体的状态，给落锤施加一个冲击速度，大小可简化为随不同冲击高度自由落体的速度，由于土体材料为Mohr-Coulomb模型，考虑了土体的塑性变形，故两者的冲击碰撞为非弹性碰撞。由于落锤冲击速度为低速冲击，且产生的冲击力在土体内有所衰减，导致管道产生的应变较小，为低速动态变形，故不用考虑材料的应变率效应。

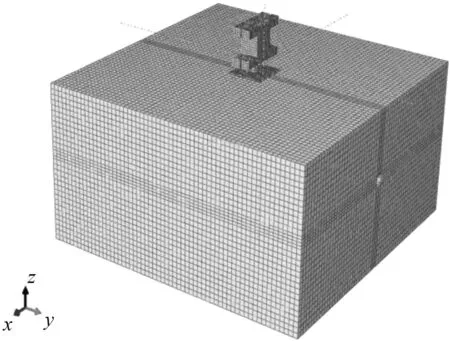
(a) 土体网格划分

(b) 管道网格划分

图16 模型网格划分
Fig.16 Model meshing

3.2 有限元模拟与试验数据对比分析

图17中(a)和(b)分别为试验和有限元模拟的管道应变对比，可以看出，有限元模拟的管道应峰值变值与试验测得管道峰值应变值基本吻合，随冲击高度的增加，管道峰值应变增加，在冲击高度1.0 m之前，管道应变变化明显，随后变化趋势变缓。图17 (c) 、17 (d) 和17(e)分别为不同管壁、管径和埋深下的有限元和试验结果对比，可以看出，有限元的计算结果与试验测得数据结果比较吻合。在埋深对比中，有限元埋深较浅的管道应变略大于试验值，这与土体离散型有较大关系，下部土体压实较上部土体更密实，但总体上有限元的数值模拟较合理，具有可行性。图17(f)为管道在不同埋深条件下有限元模拟与实验结果的对比关系，由图可以看出，在有限元模拟中管道受到的冲击能量一定的情况下，埋深为0.25 m时管道应变已达到屈服应变，且根据图中管道应变与埋深的关系，可以看出管道埋设深度为0.5～0.6 m较合理。

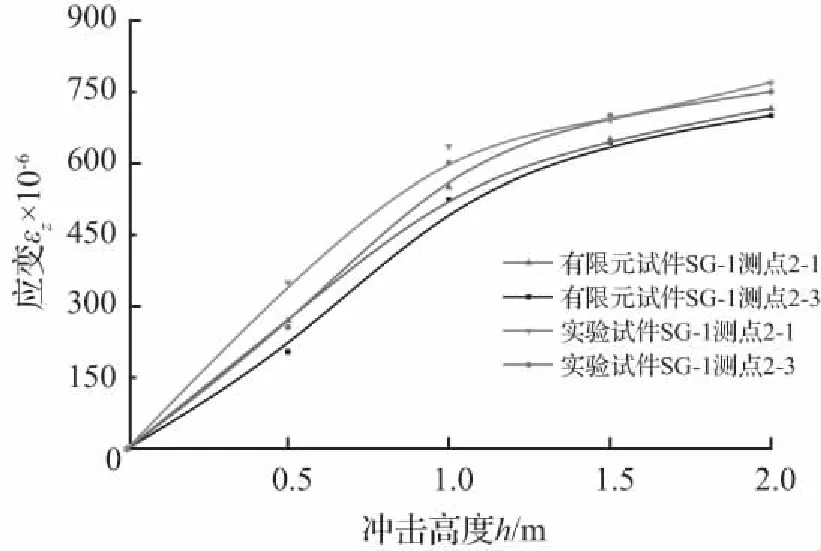
(a) 不同冲击高度试验结果与有限元峰值应变对比关系图

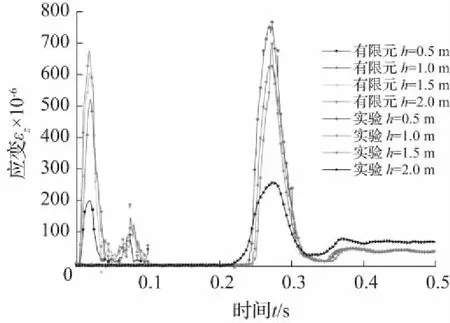
(b) 不同冲击高度试验结果与有限元应变时程对比

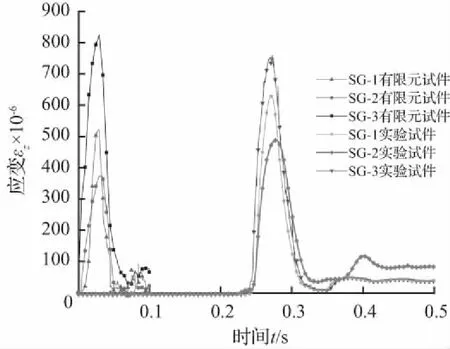
(c) 不同管径试验结果与有限元应变时程对比

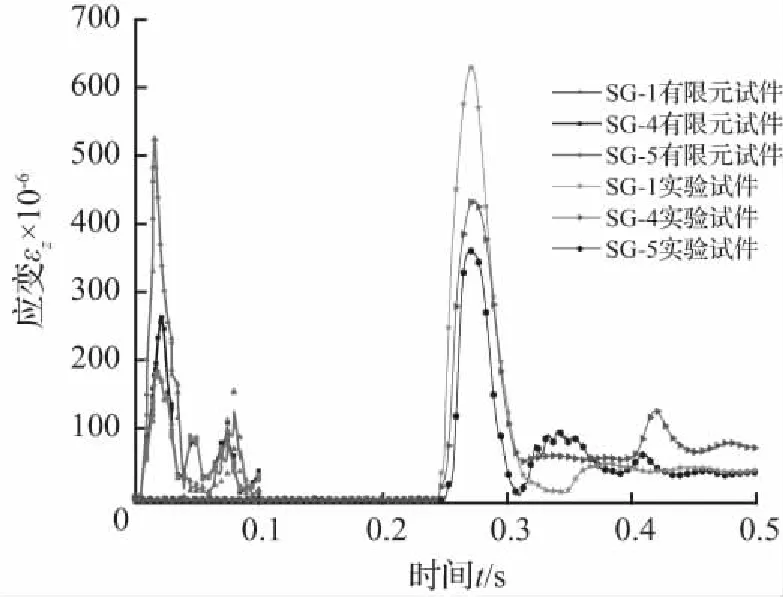
(d) 不同壁厚试验结果与有限元应变时程对比

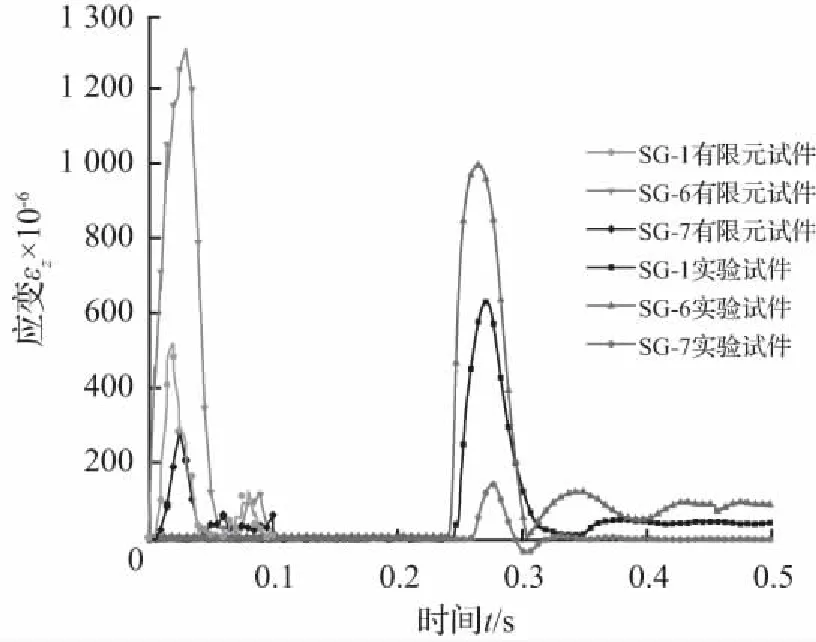
(e) 不同埋深实验结果与有限元应变时程对比

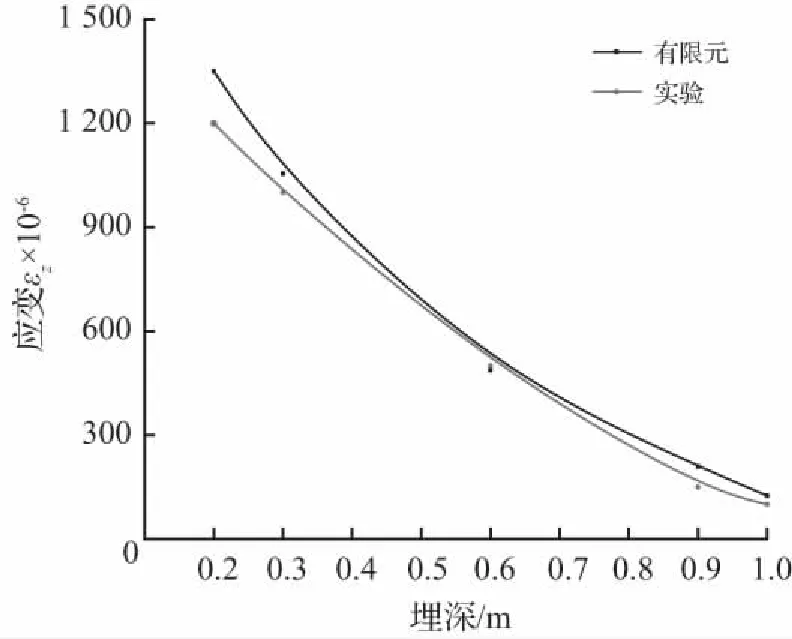
(f) 不同埋深实验结果与有限元对比关系图

图17 试验与有限元模拟结果对比
Fig.17 Comparison of experimental results and FEA

4 结论

通过对埋地管道进行落锤冲击试验和有限元模拟，探讨了埋地管道在冲击荷载作用下的应变分布规律，并分析了不同参数对管道动力响应的影响，得到如下结论：

①在落锤冲击荷载作用下，管道中部峰值应变最大，管道上下表面应变呈反对称；沿管道两端方向，峰值应变逐渐减小，且管道两端的应变相对中部呈对称分布。

②当冲击高度增加时，小管径、厚壁管道峰值应变变化较小，故可在实际工况下，选用小管径，厚壁管道，来削弱落石冲击的破坏作用。

③管道埋深越大，峰值应变越小，土体起到良好的缓冲作用，有效降低冲击荷载的影响，故在可能存在落石冲击的区域，管道不易浅埋。

④有限元分析和试验结果分析一致性较好，本文所建立的数值模型可以用来模拟落石对埋地管道的冲击作用。