自由活塞斯特林发动机的响应面法设计

冶文莲 ，王小军，刘迎文 ，闫春杰

（1.兰州空间技术物理研究所 真空技术与物理重点实验室，兰州 730000；2.西安交通大学能源与动力工程学院 热流科学与工程教育部重点实验室，西安 710049）

0 引言

自由活塞斯特林发动机（Free Piston Stirling Engine，FPSE）作为一种外燃式发动机，具有效率高、寿命长、结构简单、噪音低、不易磨损、自启动等特点。可利用热源范围广，例如太阳能、同位素能源、生物能、余热等[1]。其技术特征为：柔性弹簧支撑、无磨损间隙密封、动力活塞与配气活塞通过流体传动完成机械能的输出。在所有发动机中，FPSE的循环效率最接近卡诺循环，可以达到理论卡诺循环效率的60%[2]。

近几十年，研究人员在斯特林发动机的热力学分析方面开展了充分研究。根据Martini[3]的命名法，斯特林发动机热力学分析法大体可分为零级到四级五大类，包括用于斯特林装置初步设计优化的零级分析法，以斯密特等温分析法[4]为代表的一级分析法，以绝热分析为代表的二级分析法[5]，由Finkelestin提出的三级分析法，基于CFD软件的四级分析法[6-7]。其中，三级分析法采用节点法求解每个节点处气体工质的质量、动量以及能量守恒方程，各部件采用模块化连接，可建立自由活塞斯特林发动机整机内部气体工质瞬时流量、压力等模型，能有效预测整机的输出功率和热效率等性能参数。Gedeon[11]编制了专门的软件Sage，国内外研究学者采用此软件开展了斯特林发动机的模拟计算[8-9]，在预测斯特林发动机性能方面准确性较高，已被NASA GRC广泛采用[10-12]。四级分析法虽然在整机设计、性能优化等方面具有很好的应用，亦可直观地表示整机内部温度场、压力场、速度场等分布，但是在整机设计优化方面比较耗时。因此，本文将采用Sage软件开展FPSE的设计计算。

斯特林发动机的性能好坏主要取决于众多几何参数的选取，包括活塞杆直径、活塞直径、加热器、回热器以及冷却器结构参数等，评价斯特林发动机热力学性能的指标有输出功率、热效率，文中将其作为输出参数进行优化设计。从国内外相关文献中可知，各个参数间具有复杂的相关性，而且前期优化设计中更多的考虑了单因素的影响[13]。为了克服上述问题，文中引入一种新的方法-响应面法（RSM）[14-16]，可有效预测斯特林发动机性能。由于影响发动机性能的结构参数较多（20个及以上），为便于后期整机调试，选取活塞杆直径、加热器、回热器以及冷却器长度作为设计参数，输出功率和热效率作为响应值，揭示发动机输出功率和效率随各项参数的变化规律。

1 数学模型

1.1 模型介绍

本文研究的自由活塞斯特林发动机结构示意图如图1所示，采用β型结构。主要由冷却器、回热器、加热器、两个活塞、直线电机等组件组成。配气活塞杆穿过动力活塞，两活塞通过气体压力的交变流动自由运动，均由板弹簧支撑。由于配气活塞端温度较高，选用材料为In718，动力活塞材料为硬质铝合金。FPSE基本参数如表1所列。

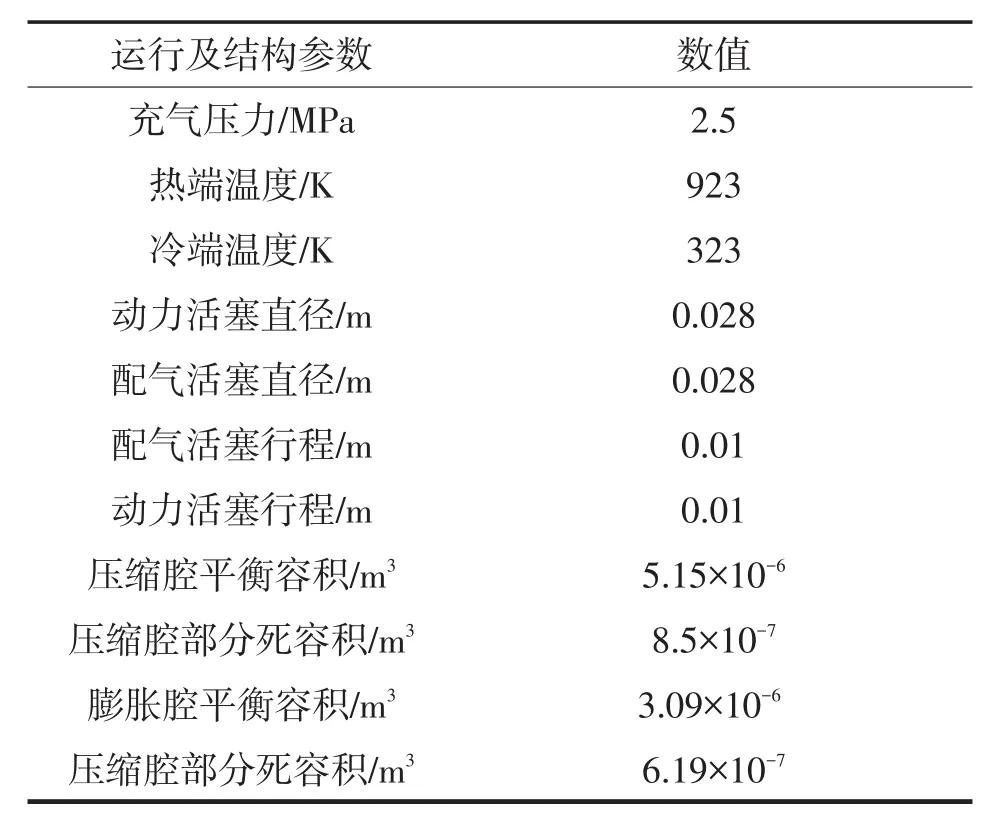
表1 自由活塞斯特林发动机基本参数Tab.1 The technical specifications of the FPSE

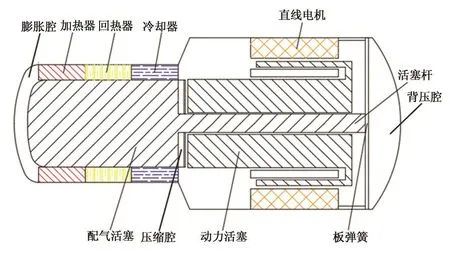
图1 自由活塞斯特林发动机结构示意图Fig.1 The schematic illustration of the FPSE

Sage软件[17]是一款用于模拟、优化斯特林循环发动机、斯特林制冷机的一维专用软件，已在回热式发动机的研究中被采用。其采用可视化界面，对发动机的各个部件一一建模，各模块之间通过质量、能量流动进行连接。根据图1的斯特林发动机结构，采用Sage对其建模，如图2所示。模型中包括配气活塞，动力活塞，环形翅片式加热器和冷却器，不锈钢随机纤维回热器、膨胀腔、压缩腔和背压腔等模块。此外，在建模过程中考虑了配气活塞处穿梭损失，回热器壁面导热损失、配气活塞壳体导热损失等，以及膨胀和压缩腔部分的死容积。各个部件间根据实际状态进行质量流、能量流的连接。模型中假设氦气为理想气体，忽略辐射漏热以及与外界环境的对流换热。压缩腔和膨胀腔外壁设置为绝热边界条件。

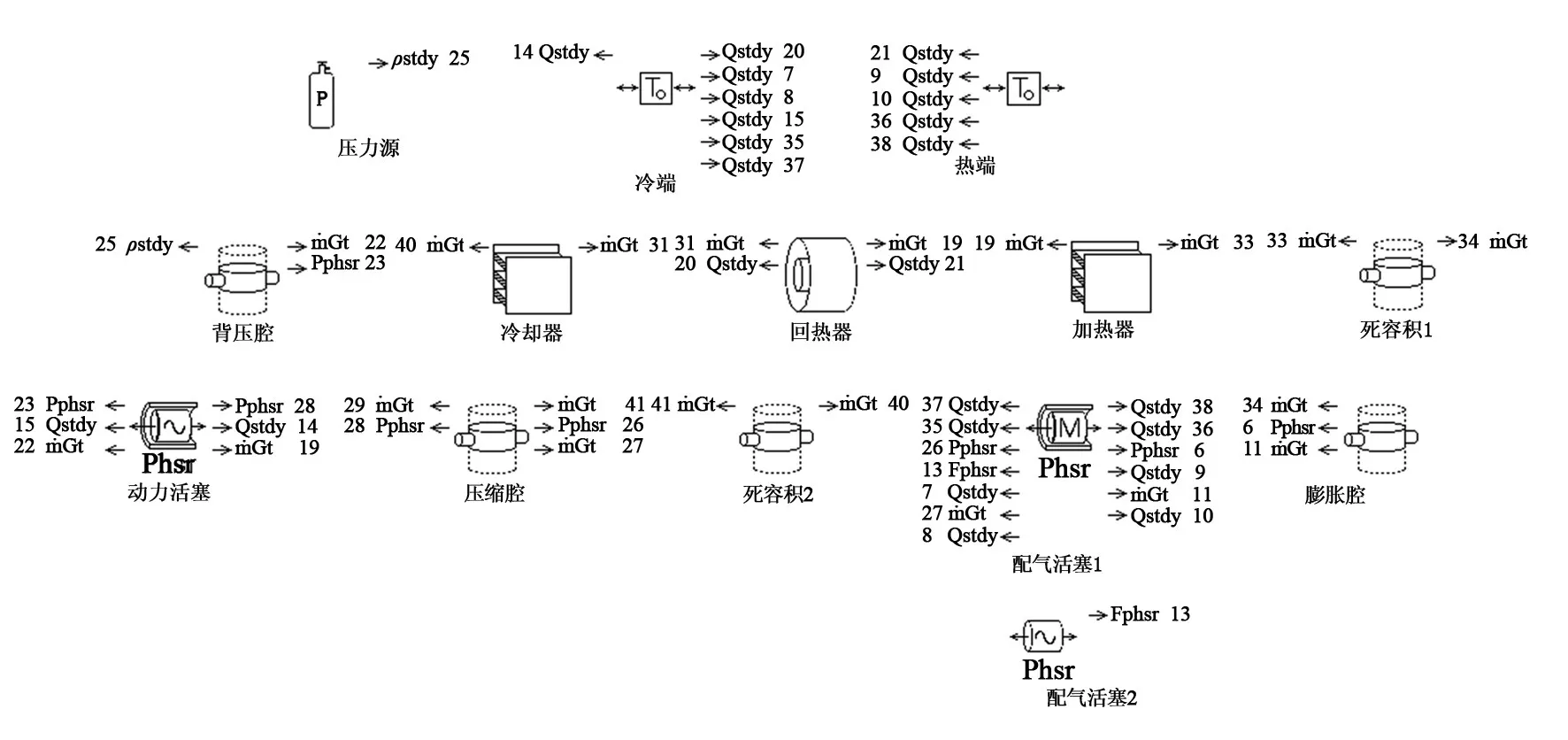
图2 自由活塞斯特林发动机Sage模型图Fig.2 Sage model of FPSE

1.2 气体动力方程

自由活塞斯特林发动机内部气体的流动和传热为非定常周期型可压缩流动。为便于说明一维流动和传热，将空间平均和时间平均的内部流动气体各方程表述为[17]：

连续方程：

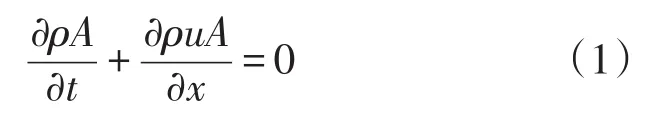
动量方程：

能量方程：

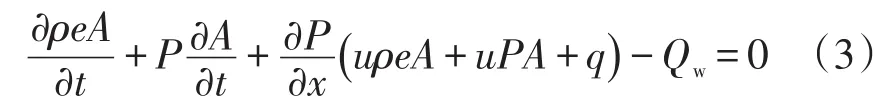
式中：t为时间，s；ρ为工质气体密度，kg/m3；A为气体域截面积，即x方向上的截面积，m2；u为流体速度，m/s；p为压力，Pa；e为质量能；q为气体轴向导热热流，W/m2；Qw为对流换热热流，W；动量方程中的F是斯托克斯的应力项，在一维方程中无法求解。可以用换热器的水力直径dh和长度L的Darcy阻力系数f和总局部损失系数K来表示：

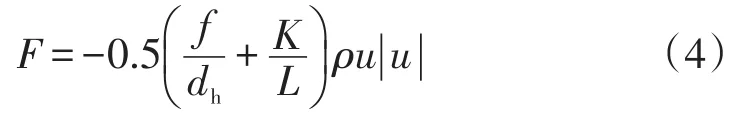
其中阻力系数根据不同换热器结构来选取，文中采用的回热器为不锈钢随机纤维结构，加热器和冷却器为翅片结构。其中回热器阻力系数表示为：

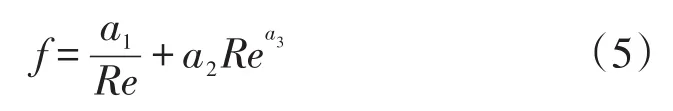
式中：a1=25.7α+79.8；a2=0.146α+3.76；a3=-0.002 83α-0.074 08；α=

加热器和冷却器阻力系数：

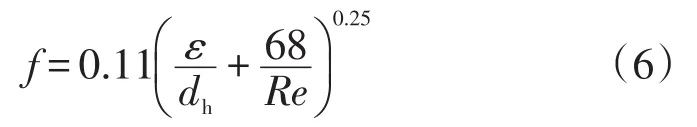
式中：φ为回热器孔隙率；Re为雷诺数；ε为表面不规则物体的平均高度。

在丝网气体区域中，能量方程中的Qw由通过截面单位长度的热流表示：

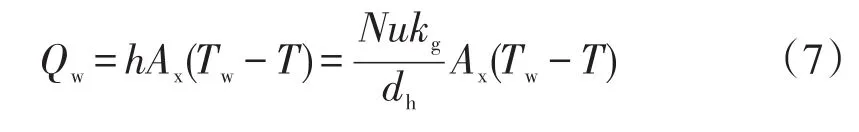
式中：Nu为努赛尔数；kg为气体的导热系数，W/（m·K）；Ax为单位长度的流体和表面接触面积，m2；Tw-T为计算流体通过表面和平均截面间的温差，K。不同类型的气体区域由于流动换热特性不同，Qw有不同的表达，应根据实际情况进行计算。

对上述气体动力方程式（1）～（3）在均匀分布的网格点上进行离散求解。在这些网格点上，变量ρ、ρuA及ρe通过隐式函数进行插值，然后在一系列网格上进行求解，再求解密度ρ以满足整个系统的动量和能量守恒。

2 响应面优化方法

响应面优化法（Response Surface Methodology，RSM），也叫响应面曲面法，主要通过对指定设计空间内样本点的集合进行有限的试验设计，采用多元线性回归的方法，将试验中的各个因素及其交叉因素进行多项式拟合，再根据函数的响应面等值线和回归方程等确定试验的较优组合。在工程优化设计中，应用响应面法可以得到响应值与输入变量之间的变化关系。RSM主要包括Box-Behnken（BBD）设计、均匀外壳设计（Uniform Shell Design，USD）和中心组合设计（Central Composite Design，CCD）三种，BBD是RSM方法中常用的试验设计方法，适用于2～5个因素的试验，文中采用BBD优化法设计试验点。采用的RSM方法主要用于评价部分关键结构参数对斯特林发动机输出功率和热效率的影响。RSM的实施过程如下：

首先，根据优化需求定义因素的水平、范围和响应值。其次，基于BBD优化方法进行相应的RSM设计得出试验组合，将这些组合值代入Sage模型中进行计算得到响应值。RSM法根据试验安排及计算结果得出二次回归拟合方程，同时对拟合结果进行方差分析（ANOVA）。根据方差分析结果判断出回归方程拟合度是否良好，若拟合度良好则认为模型可靠性高，从而进行结果分析。若回归方程拟合度较差，则需要进一步添加试验点，对其重新设计。采用RSM建立结构参数与自由活塞斯特林发动机输出功率和热效率之间的关联式。其中，二次回归模型描述如式（6）：

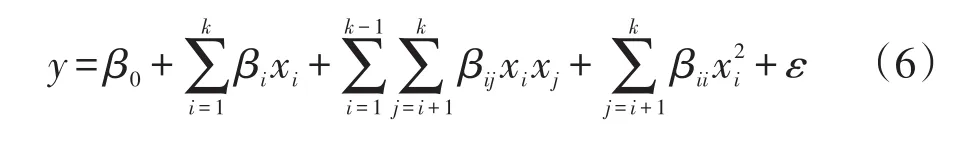
式中：y为FPSE系统的响应值；xi和xj为随机变量；β0、βi、βii和（i=0，1，2，…，k；j=0，1，2，…，k）为待定系数，由样本点迭代确定；ε为统计误差。

影响斯特林发动机热力学性能的参数比较多，包括三个换热器结构参数、冷热端温度和充气压力等。国内外研究者对这方面也做过相关研究[18，19]。在本次RSM试验中，将配气活塞杆直径、加热器、回热器以及冷却器的长度作为因变量，主要是便于后期整机热力学性能的调试，若要改动其他参数，势必给整机结构的调整带来诸多不便。回热器在实际设计计算过程中，配气活塞长度也随换热器长度发生变化。各参数的范围和水平主要基于实际工程设计，其分别由A、B、C和D表示，输出功率和热效率为响应值，分别用Wnet和Eff表示。其中，活塞杆直径范围为0.004～0.008 m，加热器长度范围0.010～0.025 m，回热器长度范围0.030～0.045 m，冷却器长度范围0.015～0.030 m，如表2所列。

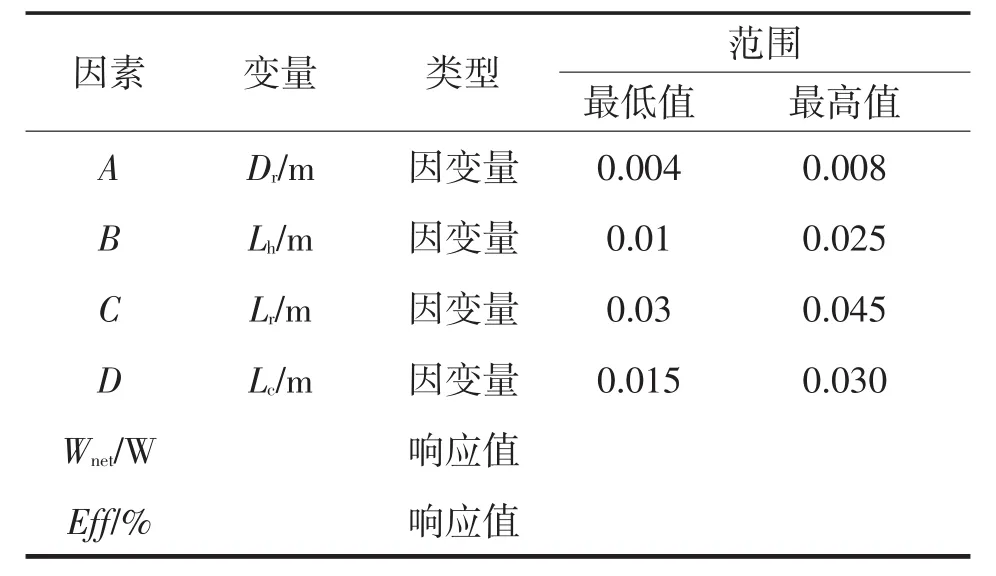
表2 各因素水平和范围Tab.2 Ranges and levels in BBD

3 结果分析

根据BBD试验设计安排试验点、各因素和水平，随机得出试验总次数为29次。将不同结构参数组合的因变量输入至Sage模型中，计算得出不同配气活塞杆直径、加热器、冷却器以及回热器长度下斯特林发动机的输出功率和热效率值，结果如表3所列。表中第1列表示试验次数，后4列表示试验条件，最后2列为试验结果。Dr表示活塞杆直径，Lh、Lr和Lc分别表示加热器、回热器和冷却器长度。对表3中数据进行回归分析，得到四因素对输出功率和热效率的二次多项回归拟合方程：

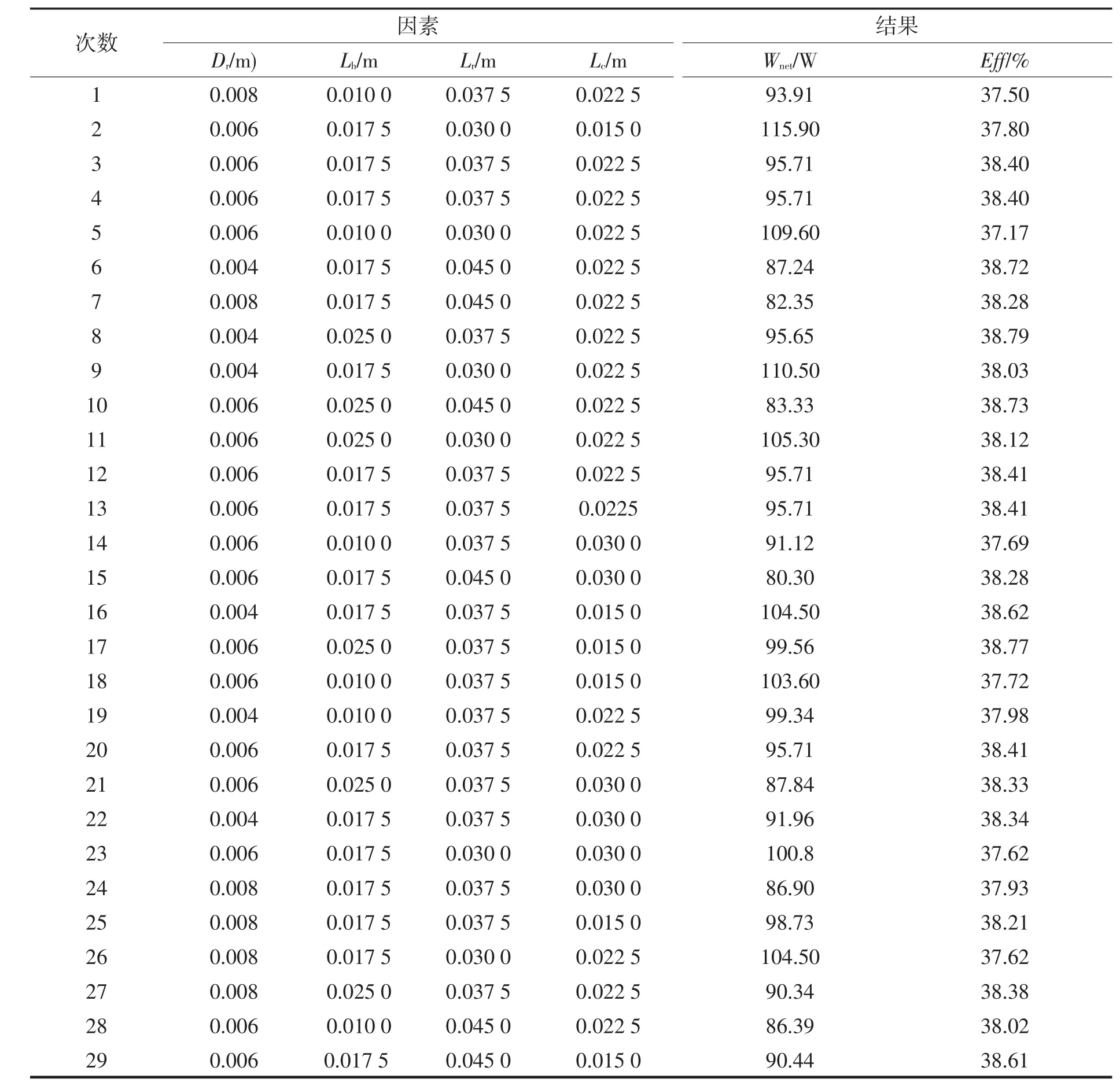
表3 试验安排矩阵Tab.3 Design of experimental matrix

3.1ANOVA分析

基于BBD算法，式（7）和式（8）给出了输出功率和热效率的二次模型回归方程。在响应面优化分析中二次回归方程的准确性和显著性由方差分析检验。表4、表5分别给出输出功率和热效率响应面优化模型的方差分析结果。平方和反映所优化试验数据的总体波动性，方差由每部分的平方和除以自由度得到，F值反映模型对响应值的影响，P值用以判断因素影响相应的显著性，P值小于0.05表示因素对响应影响很大。R2是判断回归方程有效性的一个重要参数，其值越接近于1，表明模型准确度较高。修正拟合系数R2adj反映模型能够解释的响应值变化百分比，预测拟合系数R2Pred与修正拟合系数R2adj越接近于1，表明模型越显著。信噪比用来衡量有效数据和干扰之间的比例关系，通常认为其值大于4，说明有效数据充分，模型可靠，能够准确预测响应值。由表4可知，R2为0.999 9，R2adj为0.999 8，说明模型的预测值和实际值吻合度较好。还可得知，活塞杆直径、加热器、回热器和冷却器长度及AC、AD、BC、BD、CD、A2、B2、C2和D2的P值都小于0.05，说明参数对输出功率有显著影响，而其他参数如AB的P值大于0.05，说明其影响较小。由表5可得，R2为0.998 5，R2adj为0.997 1，R2Pred为0.999 4说明吻合度较好。除了AB和AC的P值大于0.05外，其他参数对热效率都有显著的作用。由表4和表5得知，BC、BD及CD两两参数对输出功率和热效率都有显著影响，因此作为重点因素进行分析。

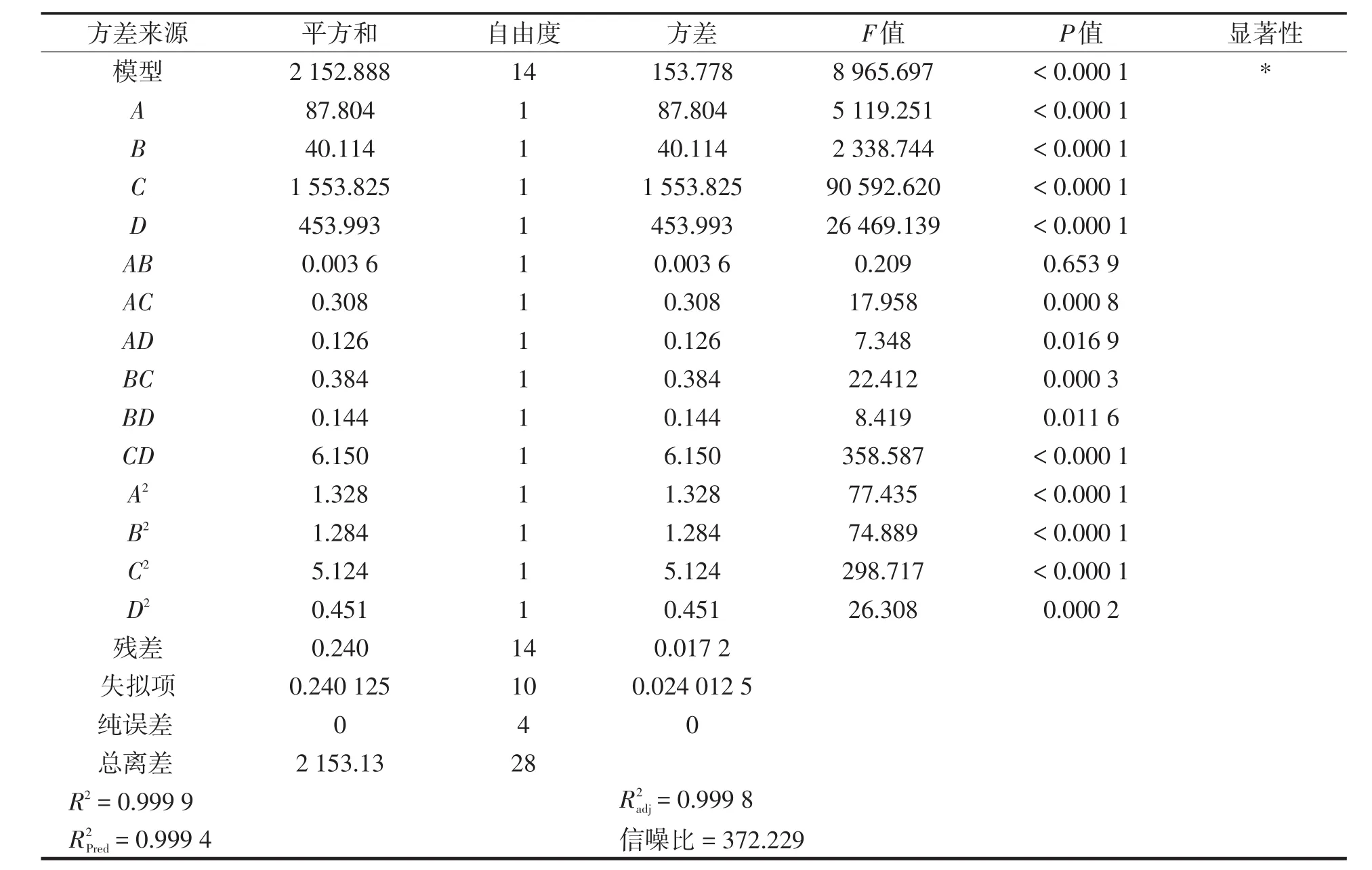
表4 输出功率的方差分析Tab.4ANOVAfor output power

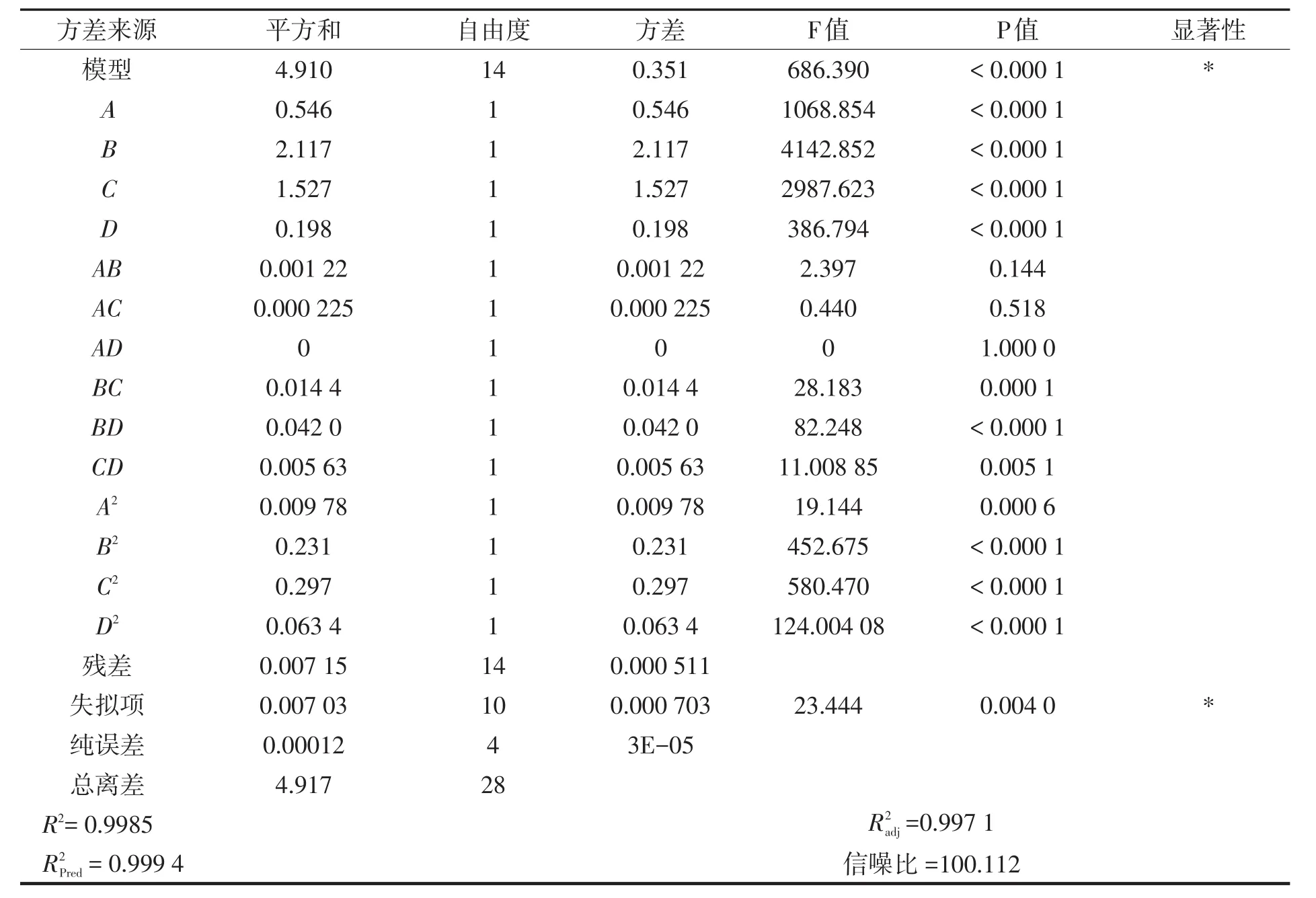
表5 热效率的方差分析Tab.5 ANOVAfor thermal efficiency

图3为响应面（RSM）预测的输出功率、热效率和Sage模型计算值之间的关系图。由图可知，大部分设计点与图中斜线十分接近，说明模型的模拟结果能够有效预测斯特林发动机的热力学性能。

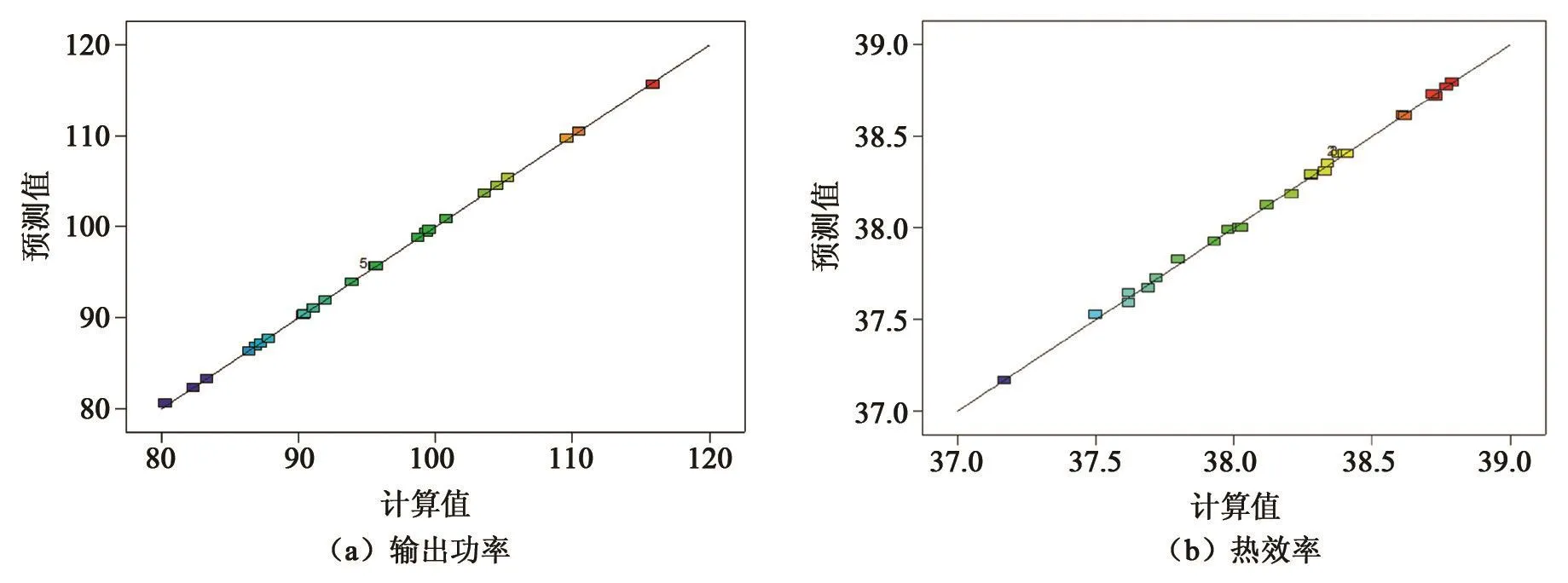
图3 响应面预测结果与Sage计算结果图Fig.3 RSM predictions versus Sage model's results

3.2 各因素之间耦合影响分析

为研究四个参数对自由活塞斯特林发动机性能的相互影响，RSM分析法提供多因素的二维等高线图和三维表面分析，显示了两个因素之间的相互作用对输出功率和热效率的影响。图4～9分别给出了BC、BD和CD（对应于表4和表5的重要因素）对输出功率和热效率的相互影响。

图4和图5为加热器和回热器长度的综合效应对FPSE输出功率和热效率的影响，此时活塞杆直径为0.006 m，冷却器长度为0.022 5 m。由图4（a）可知，当加热器长度增加至0.025 m，回热器长度最短时的输出功率最大。由图4（b）得知，加热器长度和回热器长度间的相互作用对输出功率影响较大，即两者长度增加输出功率均线性降低。从图5（a）和（b）所示的等高线和三维表面图中可看出，回热器长度增加至最大时，热效率随加热器长度增加而非线性增加。这是因为加热器和回热器长度的增加会导致流阻损失的增加，使得输出功率随之降低，但在模型中引起的回热器外壳壁面导热损失降低。因此，针对实际机型，需选择合适的回热器和加热器长度。

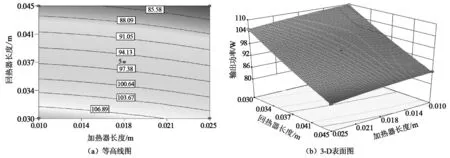
图4 加热器与回热器长度对输出功率的耦合影响图Fig.4 The combined effect of length of heater and regenerator on output power

图6和图7显示加热器和冷却器长度的综合效应对输出功率和热效率的影响，此时活塞杆直径为0.006 m，回热器长度为0.037 5 m。由图6（a）中可清晰地看出，左下角区域为输出功率的最大值，该值大于100 W，此时的加热器长度为0.015 m，冷却器长度为0.01 m。由图6（b）可知，加热器长度由0.025 m降低至0.01 m时，输出功率随冷却器长度的增加而减小，并呈现线性趋势。从图7（a）和（b）所示的等高线和三维表面图中可以看出，加热器长度增加至最大时，热效率随冷却器长度先增加，达到最大值后降低。这是因为当冷却器长度比较短时，压降损失影响不明显，输出功率降低亦不明显，热效率增加。当换热器长度增加到一定值时，由流动阻力引起的压降损失对发动机性能的影响变大。因此，发动机性能随冷却器长度的增加有最佳值。

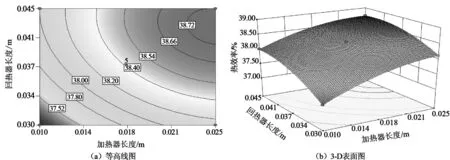
图5 加热器与回热器长度对热效率的耦合影响图Fig.5 The combined effect of length of heater and regenerator on thermal efficiency

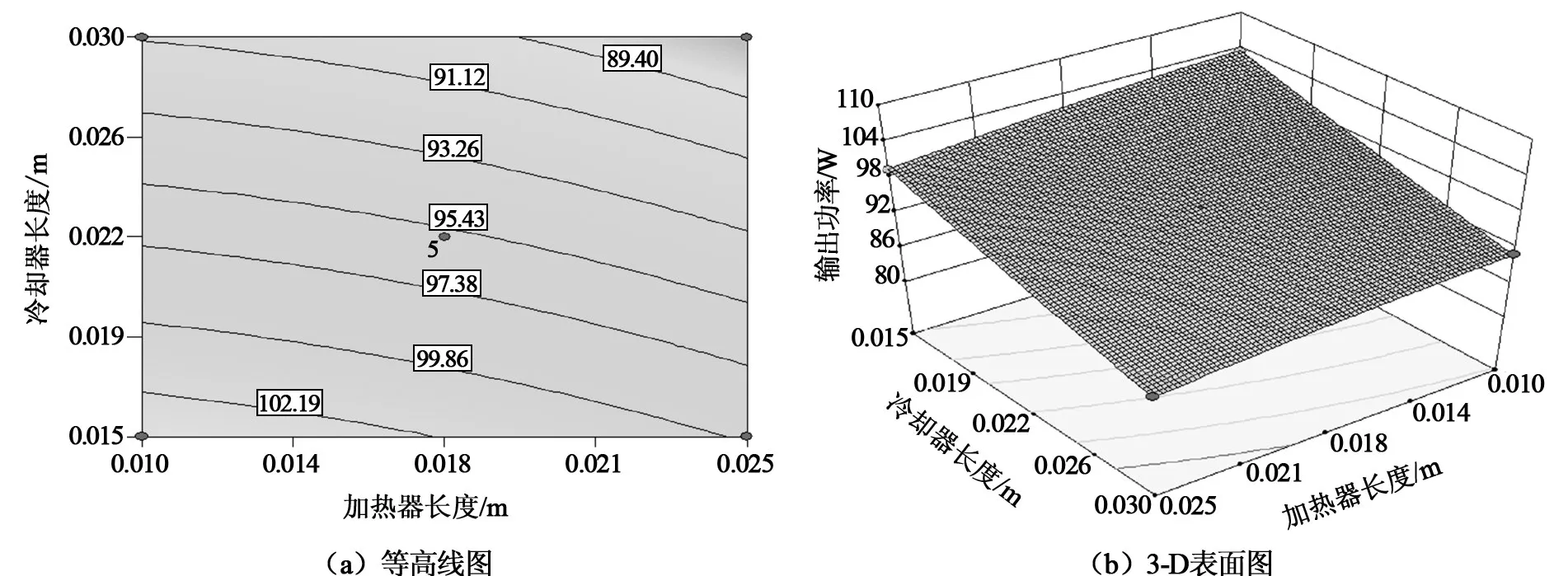
图6 加热器与冷却器长度对输出功率的耦合影响图Fig.6 The combined effect of length of heater and cooler on output power

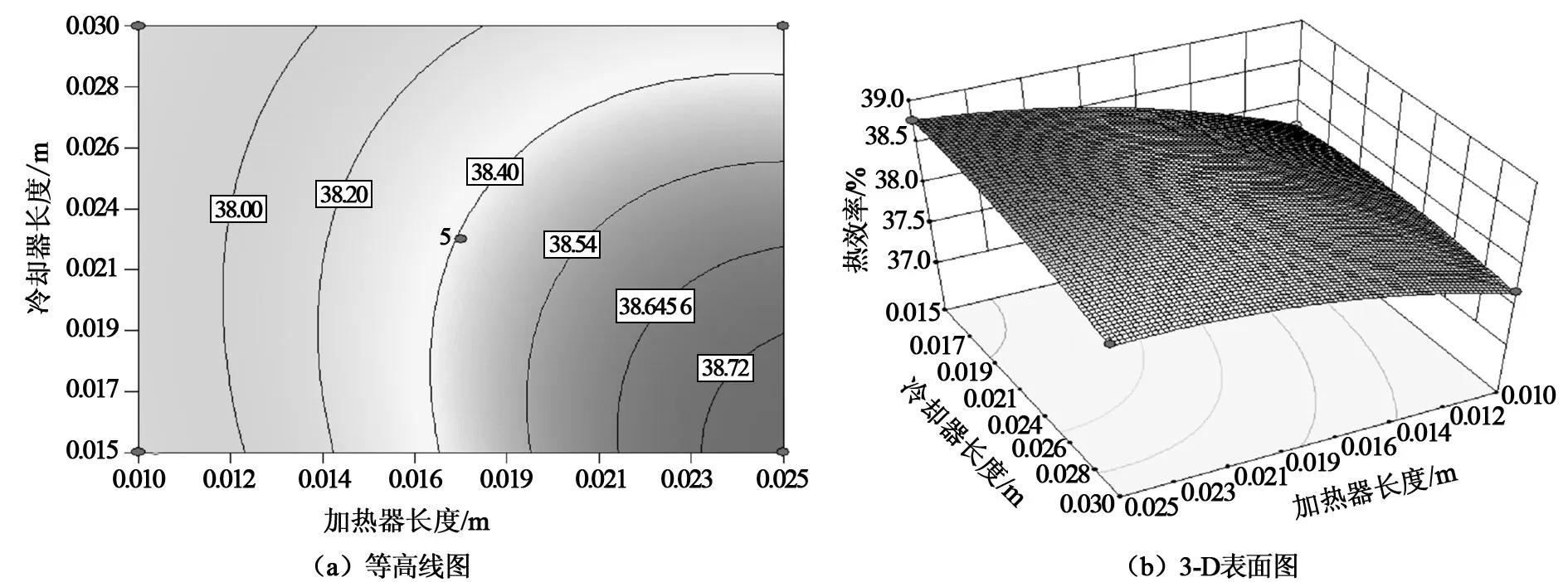
图7 加热器与冷却器长度对热效率的耦合影响图Fig.7 The combined effect of length of heater and cooler on thermal efficiency

图8和图9显示了回热器和冷却器长度的综合效应对输出功率和热效率的影响，此时活塞杆直径为0.006 m，加热器长度为0.015 m。由图8（a）中可知，等高线图中左下角区域的输出功率值最大，该值大于110 W，此时冷却器的长度为0.015 m，回热器长度为0.03 m。图8（b）三维曲面图中，回热器长度增加时，输出功率随冷却器长度的增加而降低，而且回热器长度的增加使得输出功率的降低幅度更大。由图9（a）和（b）所示的等高线和三维表面图得知，回热器长度增加至0.045 m时，热效率随冷却器长度呈二次曲线形式增加。因此，综合考虑发动机性能，应该根据实际结构设计以及后续加工工艺等因素选择合适长度的回热器和冷却器。

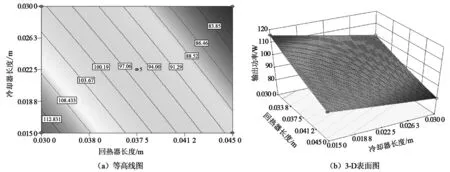
图8 回热器与冷却器长度对输出功率的耦合影响图Fig.8 The combined effect of length of regenerator and cooler on output power

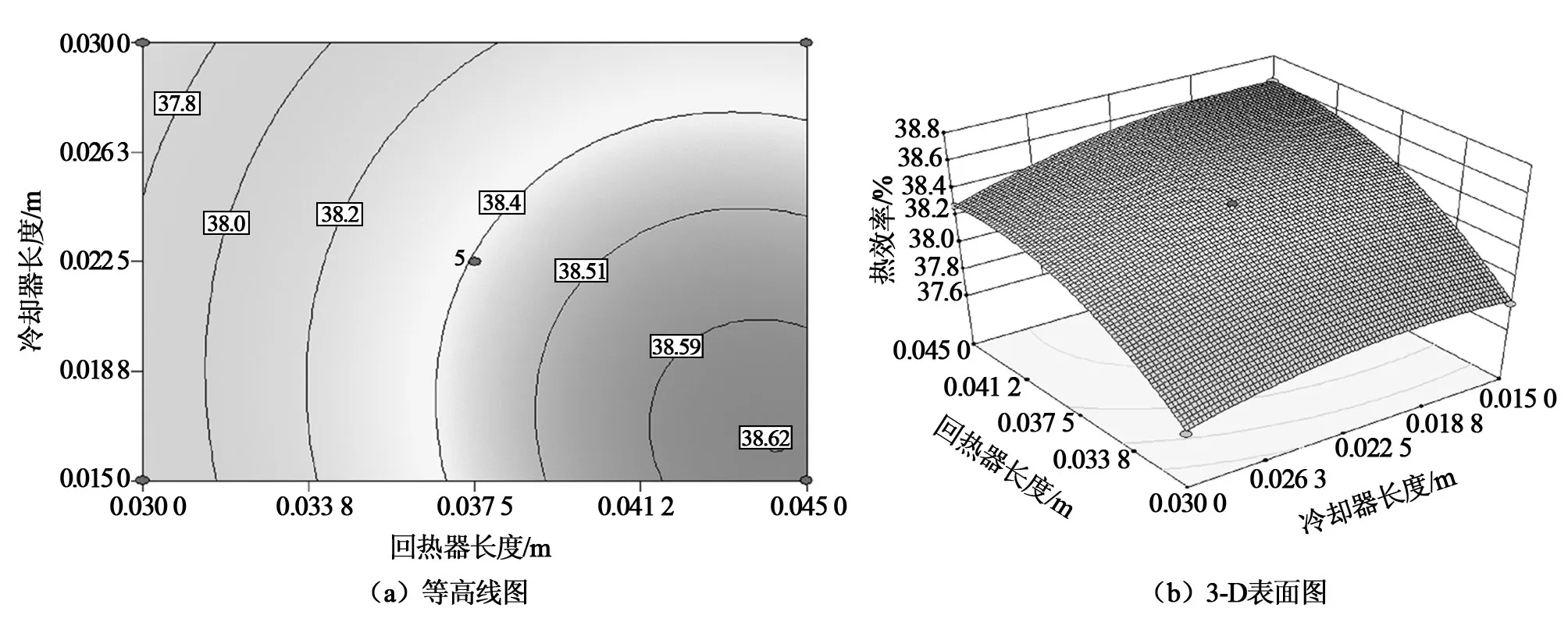
图9 回热器与冷却器长度对热功率的耦合影响图Fig.9 The combined effect of length of regenerator and cooler on thermal efficiency

4 结论

响应面是一种综合试验设计和数学建模的优化方法，可有效减少试验次数，给出比较直观、简单易懂的等高线图和三维立体图，并可有效考察影响因素之间的交互作用。通过采用RSM揭示了自由活塞斯特林发动机换热器以及配气活塞杆结构参数对整机热力学性能的耦合影响规律。得出结论如下：

（1）基于BBD方法安排了29次试验矩阵，建立输出功率和热效率的二次回归模型。通过对回归方程的方差分析和模型诊断，发现所选的四个结构参数对斯特林发动机性能具有显著影响。响应面预测模型与Sage计算结果具有高度一致性，有效证明了模型的有效性和可靠性。

（2）由RSM的二维等高线图和三维表面图，探明了两个因素之间的相互作用对输出功率和热效率的影响规律。结果显示：输出功率随着回热器、加热器以及冷却器长度的增加而降低，热效率随之增加而增加，冷却器长度对热效率有最佳值，较长的换热器长度会对整机热效率产生积极影响。在以后对FPSE的改进设计中，需合理选择其长度，以优化发动机性能并使结构更紧凑。本文对于有效设计斯特林发动机结构参数以及预测其性能具有良好的指导意义。