多平台纯方位信息融合结构及关联估计联合优化模型*
2019-08-27李洪瑞丁迎迎
李洪瑞,丁迎迎
(江苏自动化研究所,江苏 连云港222061)
0 引言
数据关联(data association,DA)起初为单传感器多目标跟踪中的一个概念和关键技术[1],在信息融合中,单、多平台的航迹、点迹或点迹序列(包括纯方位测量系统的方位序列)的融合同样存在关联问题[2],即航迹关联、点迹关联等,本文还称为数据关联。融合系统中,在将不同平台的数据进行关联后,进行的状态估计或融合估计可以获得更精确可靠的目标状态参数。因此,数据关联与状态估计直接影响着信息融合的性能,是信息融合中的难点和关键,通过不断地发展和进步,已适合各种融合系统和非线性估计场合,如用于数据关联方面的JPDA、极大似然、最近邻法、整数规划等,用于状态估计的最小二乘滤波、卡尔曼滤波、粒子滤波、无味滤波等[3]。传统融合问题中,数据关联和状态估计是不同时序的两个处理过程,即所谓的分步处理方法,即通过数据关联对数据(如测量、点迹或航迹)进行分类,然后采用有效估计方法对目标状态进行更高精度的估计[4-5]。状态估计的质量建立在关联正确基础上,数据关联错误不仅直接导致虚假目标、遗漏目标,而且影响着目标参数估计精度,因此,一些算法将融合结果进行反馈以期修正关联和改进估计结果。
在多平台纯方位信息融合系统中,因为目标方位量测是相对不同观测平台的不完全的、相对的量测量,因此,在融合过程中存在以下困难[6-11]。
1)难以对不同平台方位进行时间和空间一致处理。在不同平台测量的目标方位是相对本测量平台的不完全相对量测量,很难把它们统一到一致的坐标系中。同样,也很难在时间上进行统一。因此,一些文献要求不同平台进行时间同步观测。
2)难以用方位比较进行数据关联。由于不同观测平台探测同一目标方位的期望值并不相等,无法对方位量测进行比较确定它们是否源自同一目标,这和单平台方位信息,融合情况不同。
3)难以消除虚假目标。当多个平台探测到多个目标方位时,通过关联构成的可能目标个数(随着平台和目标数的增加)成组合增长,其中大量的目标为方位线交叉点上的虚假目标,造成大量计算,而且消除困难。
4)定位与关联相互依赖和制约。原理上,在定位与关联两个处理过程中,若能解决其中之一,则另一个也相继解决。但是,在没有进行关联时,单平台纯方位系统是不可观测的,目标运动参数是否有解完全依赖观测平台的有效机动;而目标运动参数不确定的情况下,只有方位/序列,诸如上面所描述,根本不可能对不同平台方位/序列建立关联关系。因此,对数据关联与目标定位问题采用传统分步处理方法处理,存在原理相悖。
对于多平台纯方位信息融合系统,由于以上的各种困难,传统方法难以有效应用。本文首先提出了一种基于多平台数据互联与参数估计联合优化的分布式多平台纯方位信息融合结构,然后建立了分层联合优化模型,并对该模型的计算复杂性进行了仿真计算及分析,结果表明本文提出的信息融合结构合理、模型有效。
1 问题描述
1.1 关联问题
如图1所示,各个观测平台对本地传感器探测的方位信息进行融合,得到目标方位序列或航迹(在观测平台没有有效机动情况下一般为方位序列),然后在融合中心将所有目标信息进行关联、估计处理,得出各个目标的运动参数。
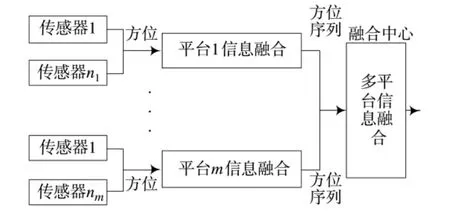
图1 分布式多平台信息融合结构
2)第i列的非零元素为1,2,…,ni,在本列中出现也仅出现一次。

1.2 估计问题
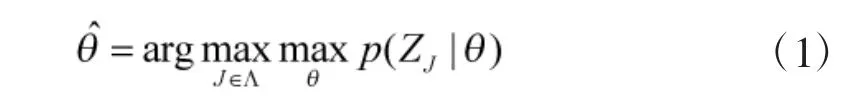
由于对各目标的测量相互独立,因此有:
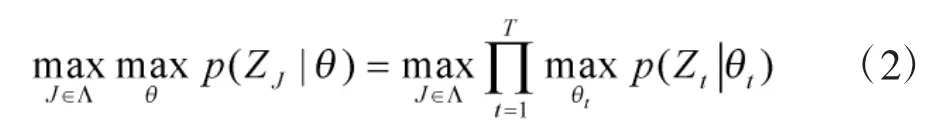
这是个非常复杂的计算难题,仿真计算表明,当平台数目大于3、目标数目大于5时,一般计算机系统难以承受。
2 信息融合结构及模型
2.1 分层信息融合结构
图2所示为融合中心所采取的分层信息融合结构。在融合处理中心依序对各平台输出方位序列采用联合优化模型进行数据关联与参数估计融合,在最后一个节点输出融合结果。
这种处理结构由于每个融合节点考虑了两个平台信息,因此,解决了单平台测量系统的不可观测问题,同时由于只有两个节点,相比多节点融合系统,又大量减少了融合处理计算量。
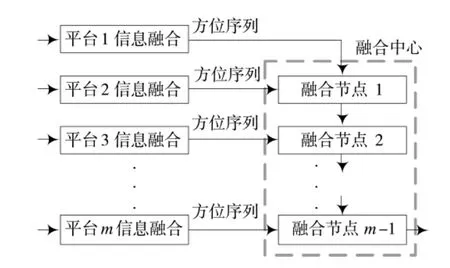
图2 融合中心分层信息融合结构
2.2 联合优化模型
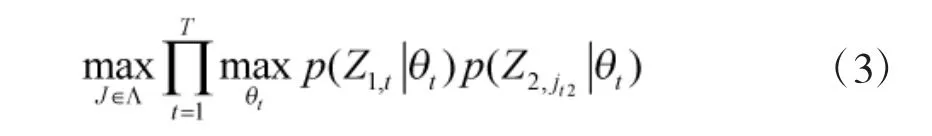
其中,T为目标个数。在这种情况下,每个融合节点的互联解空间的元素个数一般不超过T!,整个融合系统可能的关联总数不超过(m-1)·T!,因此,组合数将大量减少。
3 计算复杂性分析
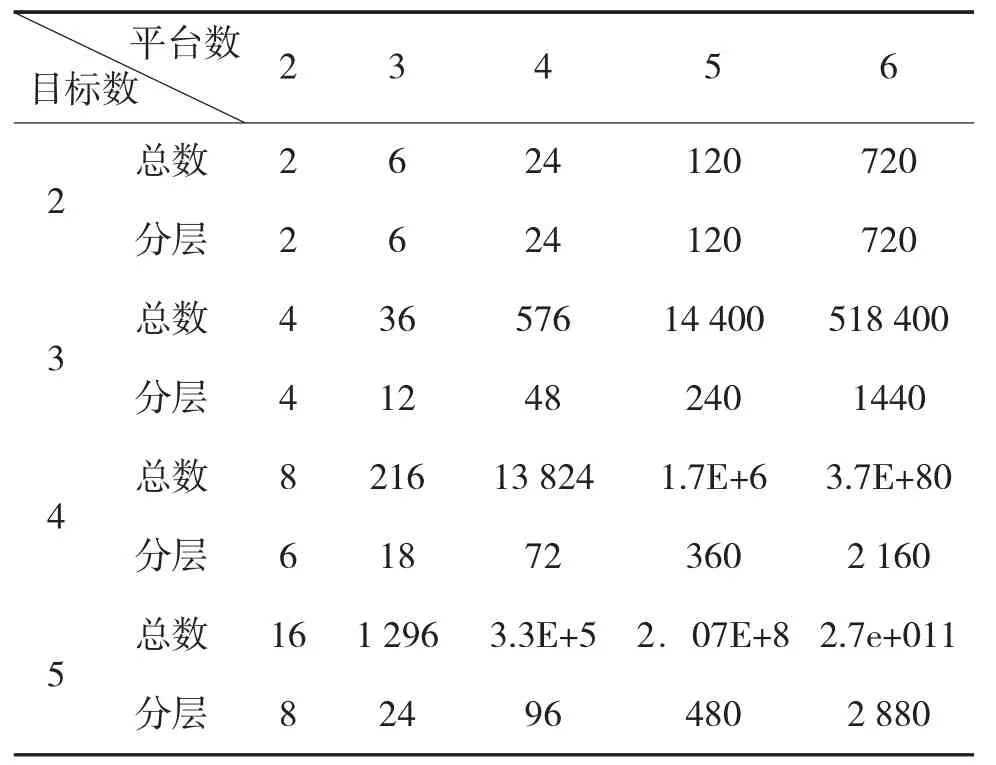
表1 目标总数和分层融合目标数随平台数变化情况
从表1可知,在平台数为3、目标数为6时,如果完成一次寻优计算耗时1 ms,那么一个计算周期的信息融合处理需要耗时约8.5 h,显然工程中是不允许的。采用分层融合时耗时只需1.44 s。
4 简化措施
从表2也可以看出,随着目标和平台数的增加,计算量也在迅速增长,因此,在目标和平台数较大的情况下,采用分层全局优化融合也存在计算量过大的问题。
为了减少可能的关联数目、降低计算量,可以通过增加约束条件在式(2)或式(3)的寻优过程中将关联可行解限定于Λ的某个特定子集。对于给定的可接受的关联可信度水平ε>0,得到可行解空间:
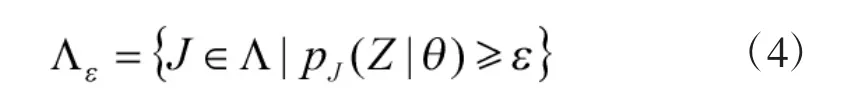
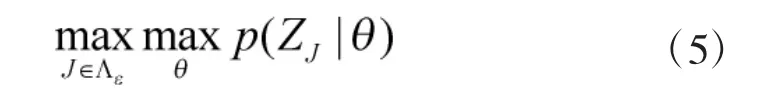
5 仿真计算
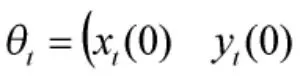
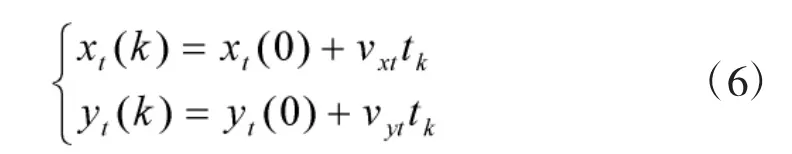
第i个观测平台对目标的测量方程为:
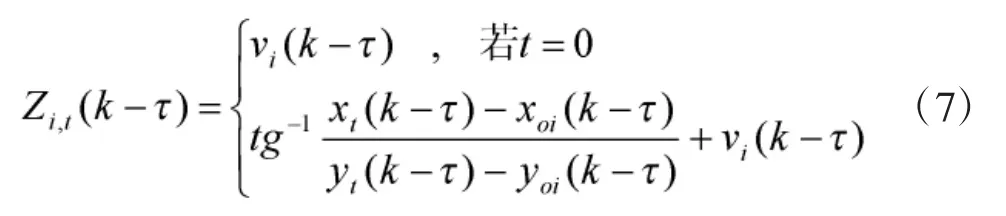
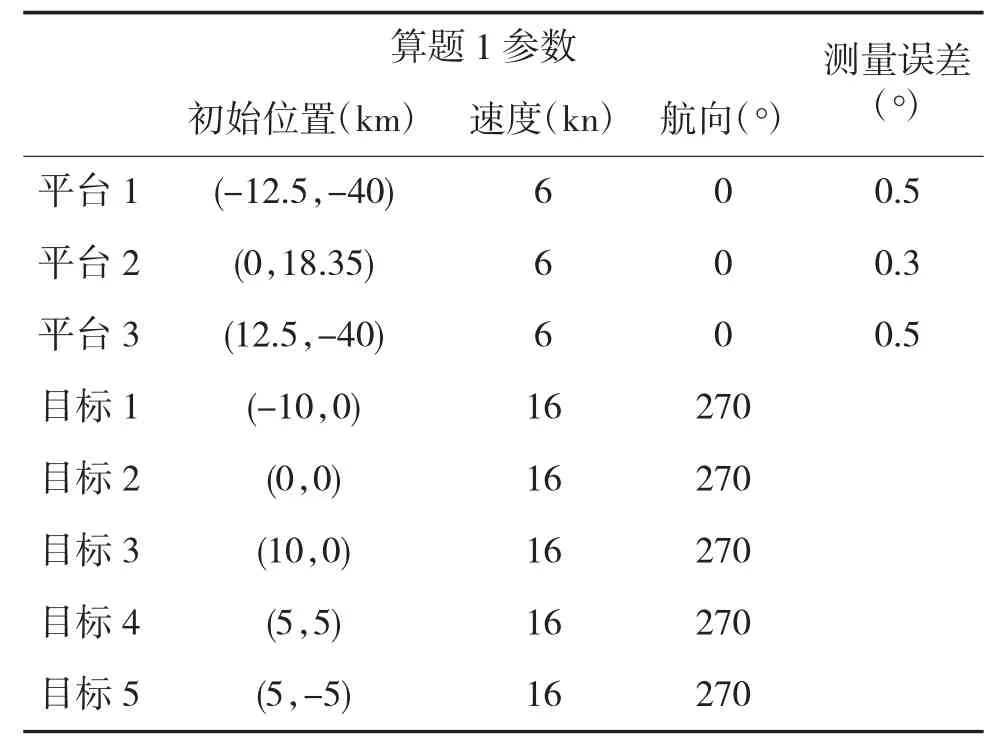
表2 仿真算题初始参数
仿真计算结果表明,在耗时方面,全局寻优时平均耗时80.13 s/周期,超过采样周期,而采用分层联合优化模型,平均耗时0.93 s/周期,省时明显。性能上,在第8 min的时候,统计的距离、速度、航向误差和正确关联率分别是180.21 m、0.65 kn、5.56°、100%和170.1 m、0.69 kn、5.67°、100%,两者相当。
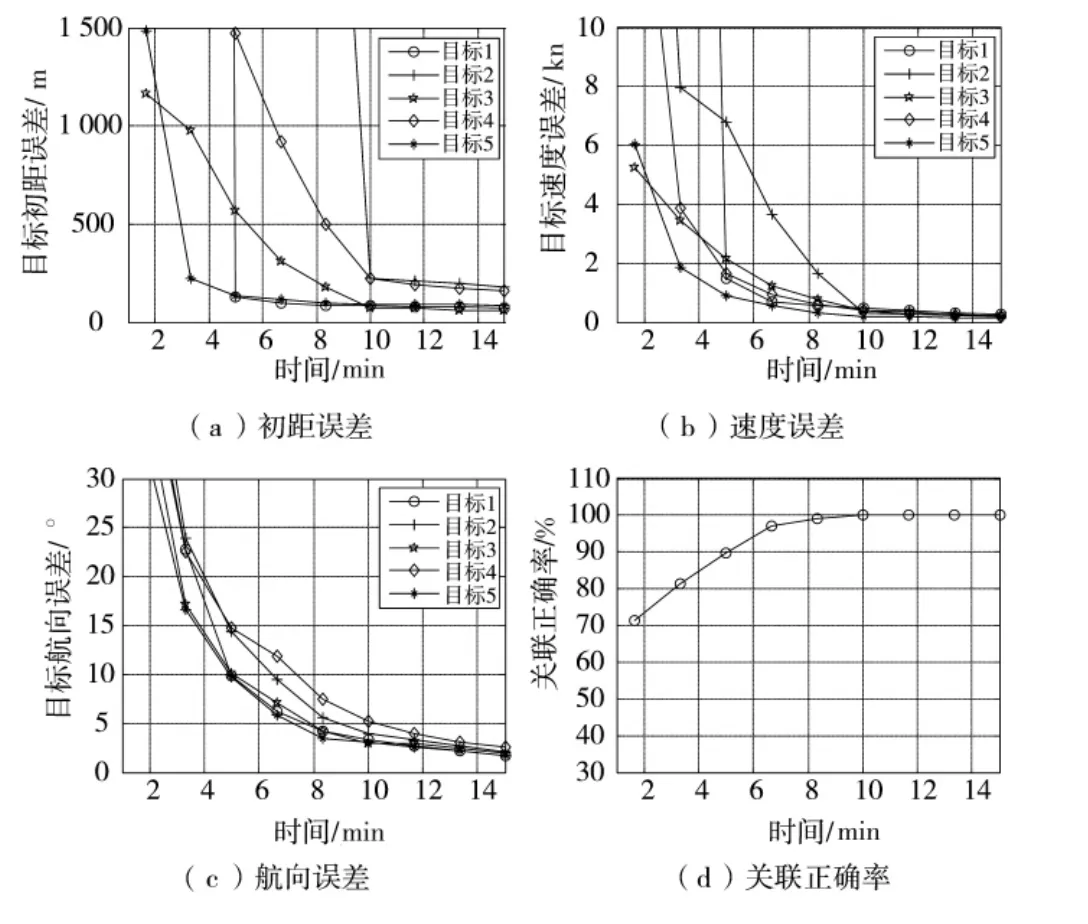
图3 仿真计算结果
6 结论
分析了多平台纯方位信息融合特点,指出其最主要难点是目标信息关联和目标定位困难,两者相互依赖和制约,约束了传统分步处理技术对两者的解决方法。本文提出了分布式的分层信息融合体系结构,建立了与此相适应的多平台纯方位数据关联与参数估计联合优化模型,即在各平台完成本地传感器方位信息融合、形成方位序列,融合中心则采用联合估计模型完成方位序列的关联融合及各目标的参数估计。将多平台数据关联与目标参数估计两个互相依赖和制约的过程有机结合,无需多个平台同步观测和机动,克服了传统方法的缺陷,较好地解决了多平台纯方位数据互联困难问题。仿真表明,所提出的信息融合结构及其联合优化模型在数据互联正确率、目标参数估计精度上均表现出良好的性能、关联和估计稳定。该模型可以应用于多平台声纳被动探测、ESM等无源探测信息融合领域。
