简捷计算无限长直电流对共面圆电流的安培力

隆勇 王胜华 李力

(重庆市清华中学 重庆 400054)

文献[1]计算了无限长直电流对共面圆电流的安培力大小，用到复分析的留数定理来处理相关定积分，计算过程繁琐冗长.本文在对称性的基础上，回归普通积分方法，极大地简化了计算，篇幅不及原文一半.

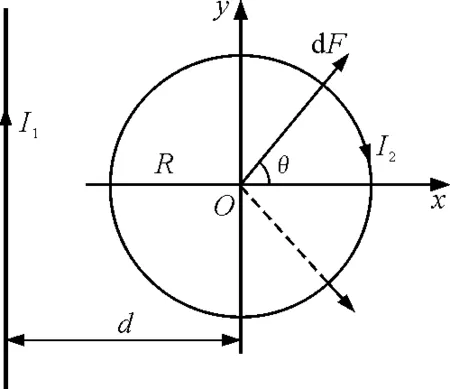
【题目】无限长直电流I1与半径为R的圆电流I2位于同一平面上，圆心O到直电流的距离为d，分别就d>R,d

图1 d>R时圆电流所受安培力

图2 d

解析：过圆心O建立平面直角坐标系，其中x轴垂直于直电流I1.在圆电流上θ处取微元Rdθ，I1在该处产生的磁场方向垂直纸面向里，大小为

微元所受安培力方向沿半径向外，大小为

由对称性易知：关于x轴对称的两微元所受安培力的y分量相互抵消，而其x分量等大且与x轴正方向同向，故只需算出上半圆周上各电流元所受安培力的x分量之和的2倍即可.

(1)

以下分别就d>R,d

当d>R时，有

d+Rcosθ=

于是当d>R时，代入式(1)得到

(2)

容易看出结果为负值，表示安培力方向沿x轴负向，从物理上看，这是直线电流I1离左半圆周较右半圆周近，故对左半圆周电流的吸引力大于右半圆周电流的排斥力的缘故.

当d

d+Rcosθ=

0-0=0

于是当d

(3)

结果为正值，表示安培力方向沿x轴正向，大小与R和d的具体数值无关，即只要I1直线与I2圆周相交，无论直线是否等分圆周，安培力大小皆为常量μ0I1I2，这是很特别的地方.

上述式(2)、(3)与文献[1]的结果完全一致，但数学方法较为简单易懂.