大跨度连续刚构参数敏感性分析
2019-08-22刘欣欣李涛马骁
刘欣欣, 李涛, 马骁
(商洛学院 城乡规划与建筑工程学院, 商洛 726000)
0 引言
苍溪县嘉陵江二桥主分左右两幅,左幅桥全长 883.8 m,右幅桥全长 884.4 m。主桥为连续刚构,布孔方案:71+2×110+63(m),边中跨比例分别为 0.645 和 0.573。中间3个主墩与主梁固结,两过渡墩顶设置活动支座。桥梁纵坡根据通航要求、堤岸防洪及通行净空要求,设计起点与现有干道接顺,终点设置 A、 B 匝道与 212国道接顺,主桥纵坡为单向 1.743%[1]。主桥桥型立面图如图1所示。
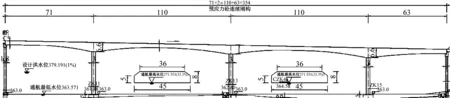
图1 桥型立面图
梁体采用单箱单室、变高度、变截面结构,箱梁用公称直径为15.20 mm 的高强度1860钢绞线做三向预应力,顶宽12.5 m,顶板厚度28~45 cm,腹板厚度45~80 cm,底板厚度30~90 cm。梁体断面如图2所示,预应力布置情况如图2和图3所示。
1 有限元模型
1.1 荷载情况
(1) 梁体自重、临时施工荷载以及二期恒载和按设计文件进行考虑;
(2) 温度变化、预应力损失、混凝土收缩徐变参数参照规范和设计文件[2];
(3) 设计文件中未给出的参数,按相关规范取值。
二期恒载和挂篮荷载,见图5、图6。
1.2 模型简化
为研究不同参数对桥梁线形和应力的影响,将相关约束条件进行简化:
(1) 节点连接:将桥墩与梁体进行“刚接”,同时对桥墩底部进行“固结”处理[3],以防止基础沉降变形对研究数据产生影响。

图2 箱梁断面图(预应力布置-桥墩)

图3 预应力布置情况-跨中
(2) 边跨支架:边跨满堂架部分的模拟,只约束了竖向位移。
边界条件见图3中端部绿色标记处,黑色表示释放该方向的约束,绿色表示约束,顺时针方向依次为DX、DY、DZ、RX、RY、RZ。
1.3 模型建立
根据设计文件和上述简化操作,建立了桥梁的Midas模型,如图4、图5、图6所示。
节点和单元编号从图3最左侧开始,节点1-115(单元1-114)为梁体单元,其中1、2节点组成了1#梁体,节点21-27为17#墩,节点55-61为18#墩,节点89-95为19#墩。全桥共计192个节点,183个单元。
图4 全桥有限元模型

图5 桥梁二期恒载
2 参数敏感性分析
对嘉陵江二桥进行参数敏感性分析,以混凝土容重、混凝土弹性模量、预应力参数作为控制变量,分别将这些参数增加+10%和+20%,每次对比只改变单一参数与参数的正常状态进行对比。以主梁内力、应力及线形作为控制目标,通过计算分析分别确定各参数对结构的影响程度,最终确定该桥线形和应力对各控制参数的敏感性[4]。为方便作图将梁体应力图单位定为N/mm2,线形图单位定位mm。
2.1 混凝土弹模
该桥主梁部分为C50混凝土,弹性模量为3.45×1010N/m2,增加10%和20%后分别为3.795×1010N/m2和4.14×1010N/m2。三种情况下应力变化情况如图7所示。
由上图可知混凝土弹性模量的变化对线形的影响主要集中合龙段前后[5],当弹性模量增加20%时,线形变化最大处位于中跨合龙段前一施工段,大小约9 mm。如图8所示。
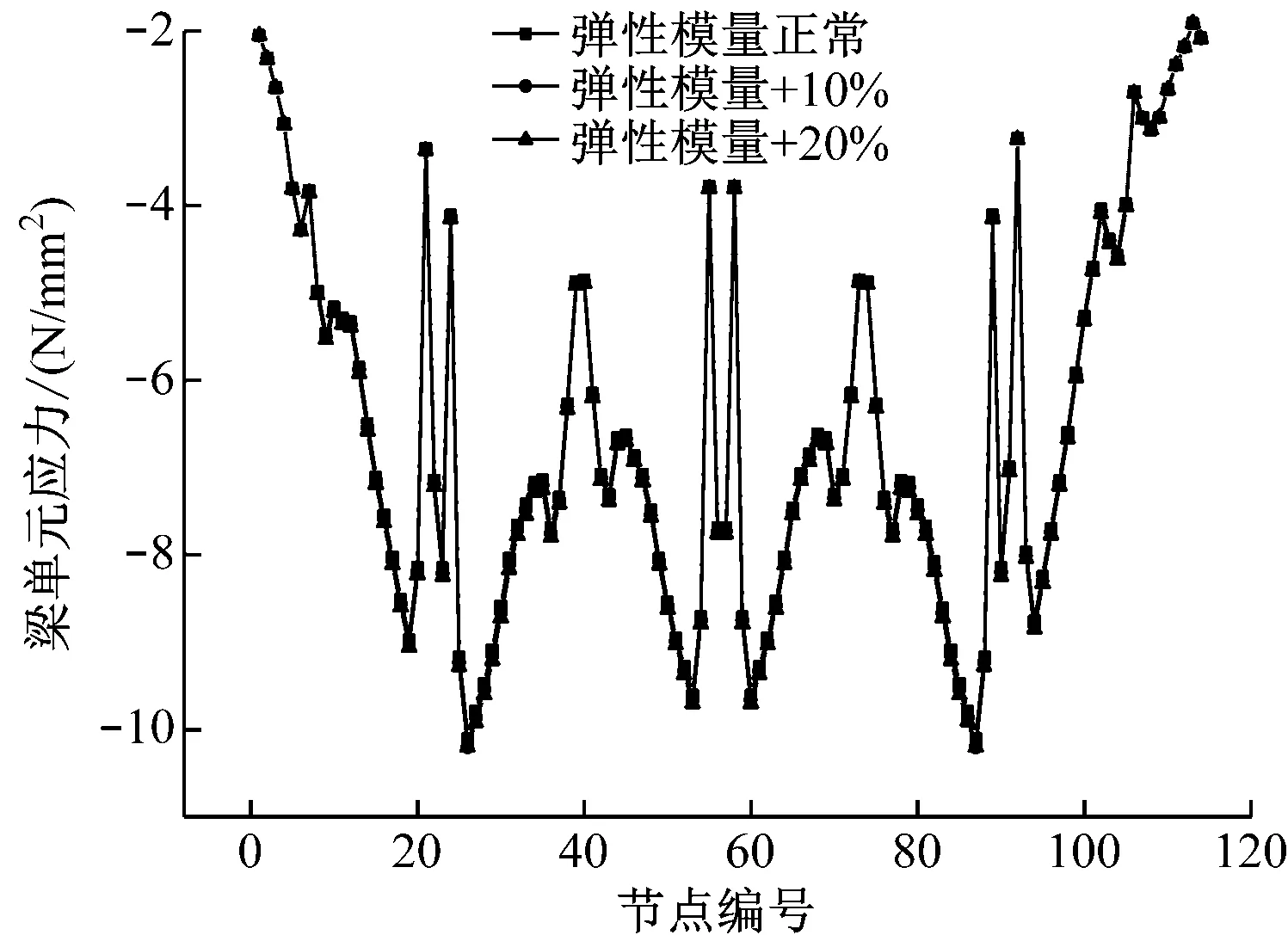
图8 弹性模量-应力变化情况
从应力对比图形可知,弹性模量对梁体的应力影响并不大,弹性模量增加20%时,桥墩处的应力变化最大约1×105N/m。
2.2 混凝土容重
模型中C50混凝土的正常容重为2.5×104N/m3,容重增加10%和20%后分别为2.75×104N/m3和3×104N/m3。容重变化后梁体的应力和线形变化情况如图9、图10所示。
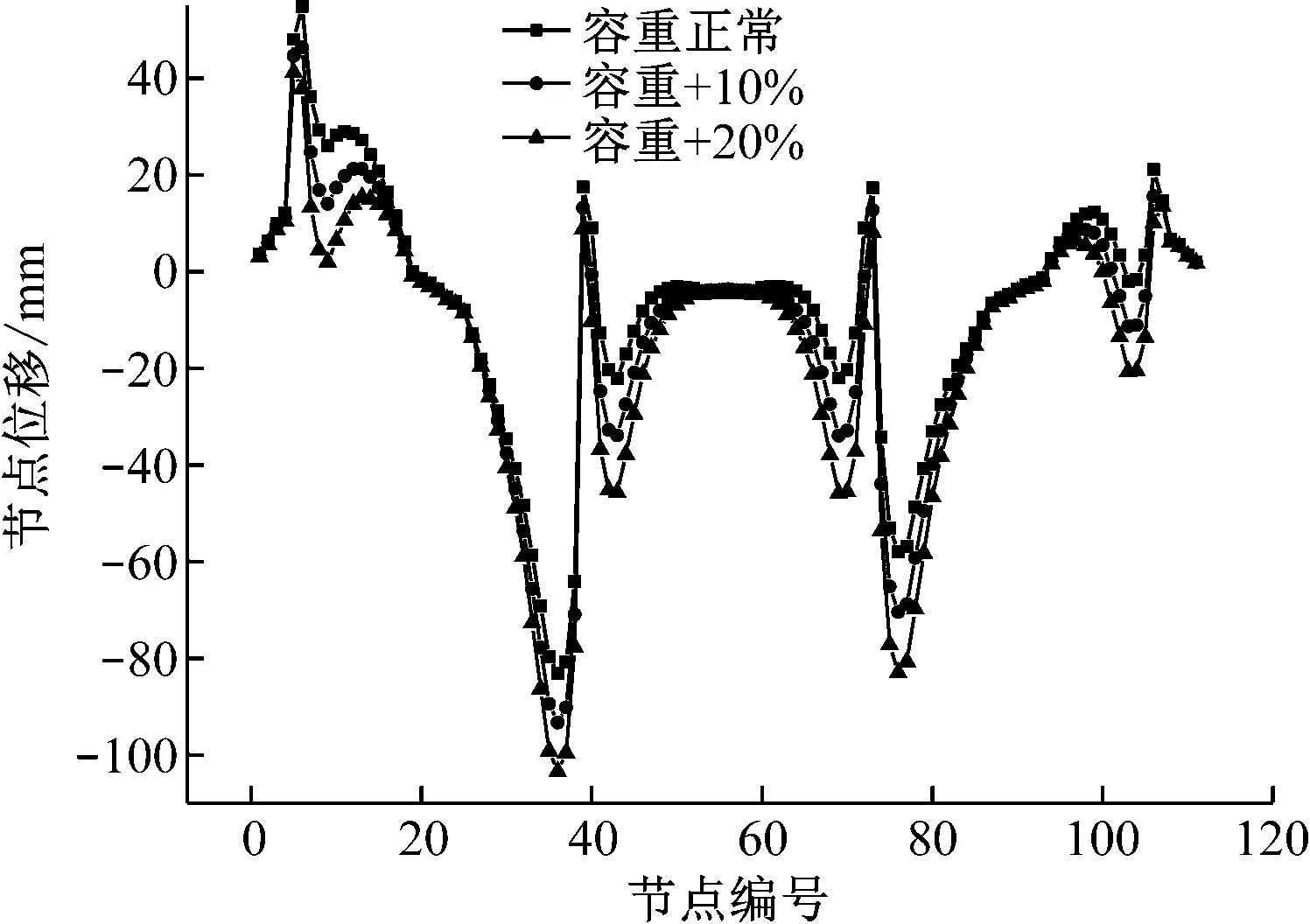
图9 混凝土容重-线形变化情况
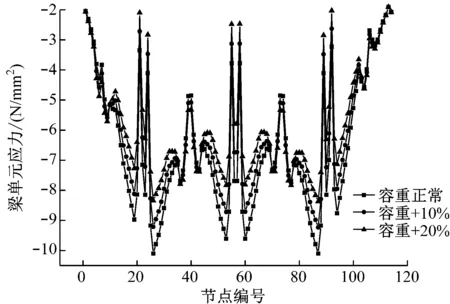
图10 混凝土容重-应力变化情况
由以上两图可知混凝土容重的变化对线形和应力的影响较为明显[6],在预应力不变的情况下,线形的变化集中在合龙段附近,最大变化约25 mm,应力的变化主要集中在1/2悬臂长度附近,约9.5×106N/m2。
2.3 预应力
本工程中所用预应力钢束为1860钢绞线,正常的张拉控制应力为1 395 MPa(75%),增加10%和20%以后分别为1 534.5 MPa、1 674 MPa。几种情况下梁体线形和应力变化如图11、图12所示。
由以上2幅图可以明显的看出,张拉控制应力的变化对梁体线形和应力都有明显的影响[7],对线形的影响在3/4最大悬臂长度处达到最大,中间跨达到23.4 mm,左侧边跨达到了34.7 mm。对应力的影响主要在桥墩附近达到最大,最大值约4.7×106N/m2。
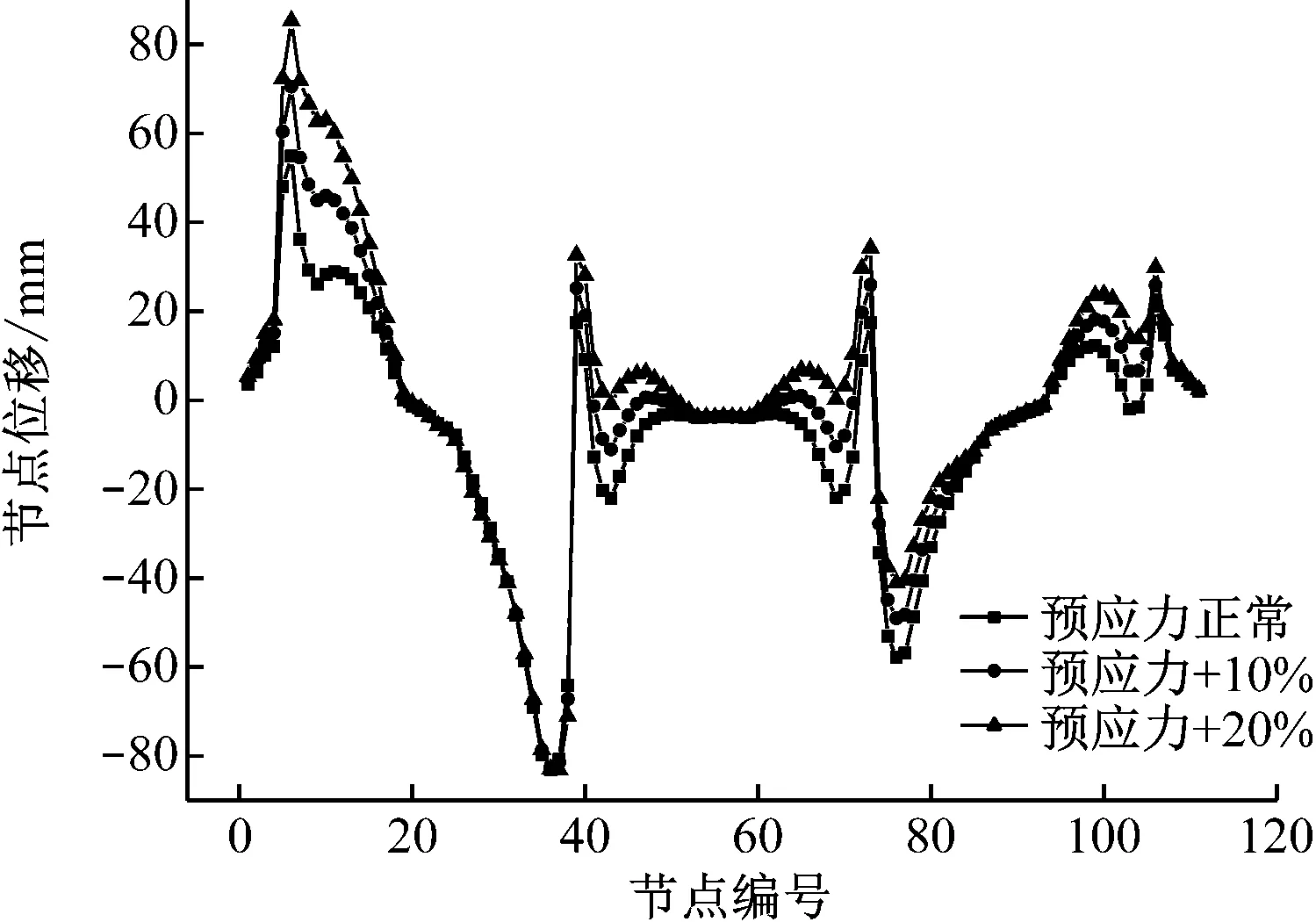
图11 张拉应力-线形变化情况
2.4 数据分析
由于未调整控制参数情况下的梁体变形(下文将此情况下的变形称为基础变形或应力)较小,最大值约83 mm,因此控制参数调整后梁体的线形变化情况并不明显。但是梁体的基础应力较大,所以调整控制参数后应力变化值也比较大。为消除基础数据的影响,将梁体线形和应力的变化过情况用百分率来表示,具体数据如表1、表2所示。

图12 张拉应力-应力变化情况
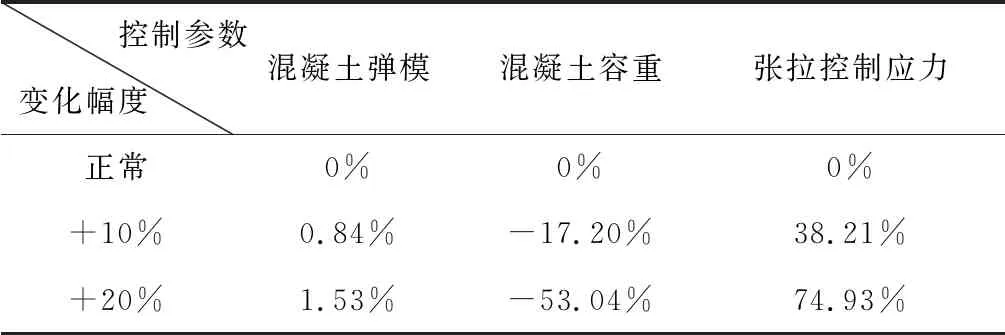
表1 线形敏感性
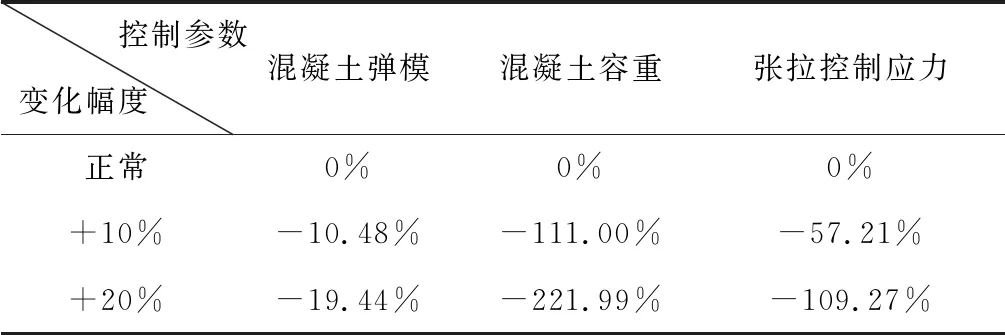
表2 应力敏感性
表1表示了控制参数对梁体线形的影响,可以看出梁体线形敏感性依次为:张拉控制应力、混凝土容重、混凝土弹性模量[8]。从图7到图12可以看出,在预应力、温度、混凝土徐变等因素不变时,混凝土容重的增加导致对应梁段自重变大,悬臂结构的挠度就有所增加,每个施工段挠度的变化会逐渐累积,最终在合龙前达到最大。由表2可以看出梁体应力的敏感性由高到底依次为:混凝土容重、张拉控制应力、混凝土弹性模量[9]。结合文中应力变化趋势可知,混凝土的容重和预应力的变化都直接影响到梁体的受力,而且悬臂结构的每一施工段均有预应力,各段的预应力都会对0#块产生影响,因此应力的变化在会逐渐累积到桥墩根部,使得桥墩处变化最为明显[10]。弹性模量的变化对梁体的受力影响较小,因此对应力的敏感性中,混凝土弹性模量排在最后[11]。
3 总结
由上文的分析可知梁体的线形和应力对预应力张拉都比较敏感,因此施工中应特别注意与预应力有关的各个环节,尤其是纵向预应力的张拉,应采用伸长量和压力值两方面的控制,此外还要注意张拉设备和机具的及时校核。施工中梁体线形的控制中应特别注意混凝土的容重的变化,以及会导致梁段自重变化的其他工序,比如模板变形、浇筑混凝土用量的控制等。
