基于非线性规划和遗传算法的函数寻优
2019-08-22王荣亮
王荣亮
基于非线性规划和遗传算法的函数寻优
王荣亮
(宿迁职业技术学院,江苏 宿迁 223800)
针对遗传算法求解复杂非线性函数寻优出现早熟,陷入最优解这一问题,将非线性规划和遗传算法相结合,通过对典型复杂函数的仿真,并与遗传算法比较,表明基于遗传算法和非线性规划的函数寻优算法具有明显的优势,收敛速度快,寻找到的极值非常接近最优解。
非线性规划;遗传算法;函数寻优;函数模型
1 引言

非线性规划大多数采用梯度下降法,局部搜索能力较强,但是全局搜索能力较弱。遗传算法具备很好的全局搜索能力,但是容易出现早熟现象,陷入局部最优解。例如上述的Ackley函数,函数具有很多极小值,很容易陷入局部最优解,如图1所示。

图1 函数图像
为了解决在上述一类函数优化时,遗传算法早熟,进入局部最优解这一问题,本文采用遗传算法进行全局搜索,非线性规划进行局部搜索,以得到函数全局最优解。
2 理论基础
2.1 非线性规划函数
非线性规划是一种求解目标函数()或约束条件中有一个或几个非线性函数的最优化问题的方法。MATLAB工具箱提供非线性规划函数,可以直接调用。函数fmincon是MATLAB最优化工具箱中求解非线性规划问题的函数,它是从一个预估值出发,搜索约束条件下非线性多元函数的最小值。函数fmincon的约束条件为:
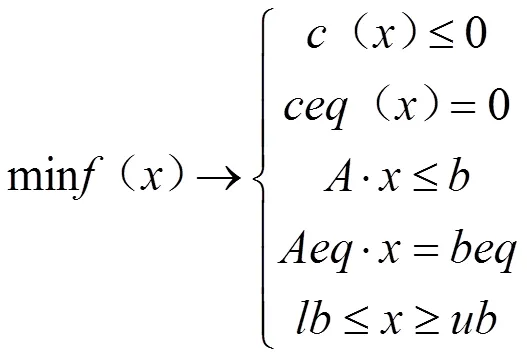
式(1)中:,,,,为矢量;,为矩阵;(),()为返回矢量的函数;(),(),()为非线性函数。
2.2 遗传算法及其基本步骤
2.2.1 遗传算法
遗传算法是一种进化算法,基本原理是仿效生物界中的“物竞天择,适者生存”的演化规则。遗传算法将问题参数编码为染色体,再利用迭代方式进行选择、交叉和变异等运算来变换种群中染色体的信息,最终生成符合优化目标的染色体。在遗传算法中,染色体对应的是数据或数组,通常由一维的串结构数据来表示,串上各个位置对应基因的取值。基因组成的串就是染色体,也称为基因型个体,一定数量的个体构成了群体。群体中个体数目称为种群大小,也称为群体规模。各个个体对环境的适应程度称为适应度。
2.2.2 基本步骤
遗传算法主要涉及的基本步骤如下。
2.2.2.1 编码
遗传算法在进行搜索之前,需要将解空间的数据表示成遗传空间的基因型串结构数据,这些串结构数据的不同组合便构成了不同的点。常用的编码方式主要有位串编码、Grey编码、实数(浮点法)编码、多级参数编码等。其中,实数编码不需要进行数值转换,可以直接在解的表现形式上进行遗传算法操作,因此本文采用该方法编码,每一个染色体为一个实数向量。
2.2.2.2 初始种群生成
随机产生个初始串结构数据,每个串结构数据称为一个个体,个个体构成了一个群体。遗传算法以这个串结构数据作为初始点开始进化。
2.2.2.3 适应度函数

2.2.2.4 选择

2.2.2.5 交叉

2.2.2.6 变异
变异主要是为了维持种群多样性。变异首先在群体中随机选择一个个体,对于选中的个体以一定的概率随机地改变串结构数据中的某个串的值。同生物界一样,遗传算法中变异概率很低,通常取很小的值,本文选取变异概率为0.01。
3 算法设计
本文结合非线性规划和遗传算法的各自有点,一方面采用遗传算法进行全局搜索,一方面采用非线性规划进行局部搜索,以得到问题的全局最优解,算法流程如图2所示。其中,种群初始化模块根据求解问题初始化种群,适应度值计算模块根据适应度函数计算个体适应度值,选择、交叉以及变异为遗传算法的搜索算子,为固定值,当进化次数为的倍数时,则采用非线性规划寻优加快进化,非线性规划利用当前染色体值采用函数fmincon寻找问题的局部最优解。

图2 算法流程图
4 实验分析
如图1所示,Ackley函数是一个非常复杂的非线性函数,存在很多局部极小值点,但是全局的极小值点只有一个0,位置为(0,0)。
分别采用基本遗传算法和本文的基于遗传算法、非线性规划的函数寻优算法进行求解Ackley函数的极小值。设定种群规模100,进化30代,交叉概率为0.6,变异概率为0.01。算法的优化过程中各代平均函数值和最优个体函数值变化如图3所示。在种群进化到20代时,函数值收敛到0.158 8,位置为(0.041 2,﹣0.032 1)。
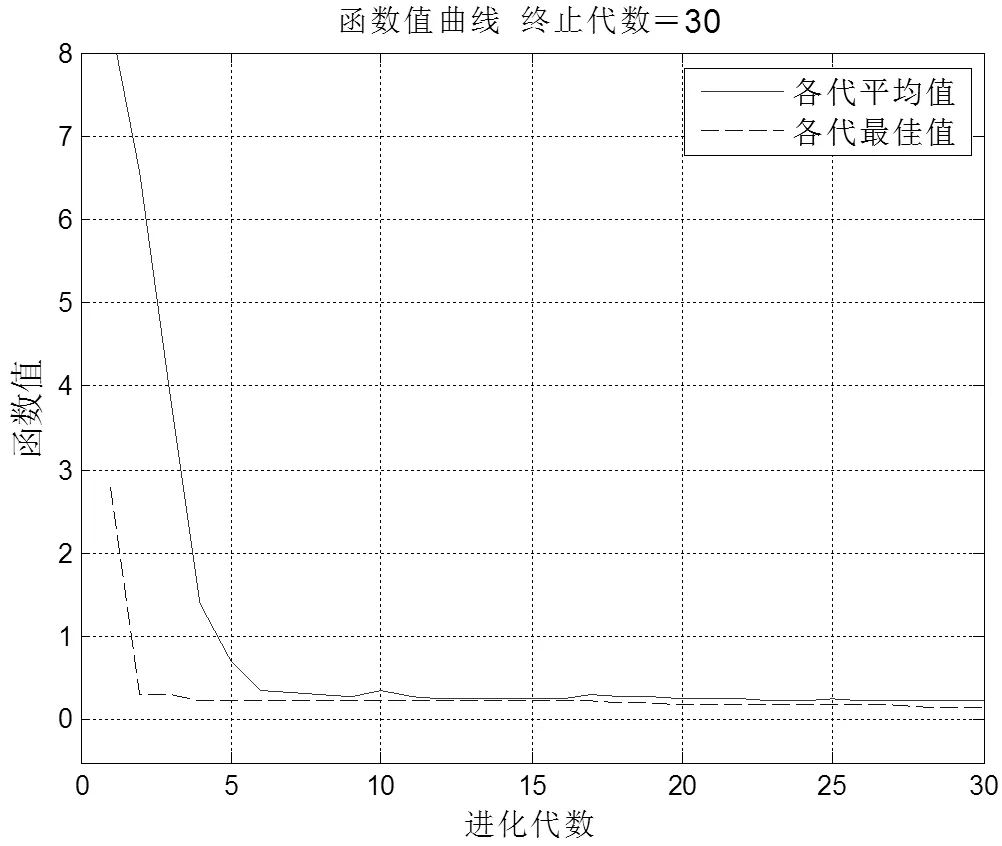
图3 基本遗传算法优化过程
用基于遗传算法和非线性规划的函数寻优算法求解,算法参数设置为:种群规模20,进化30代,交叉概率为0.6,变异概率为0.01。算法的优化过程中各代平均函数值和最优个体函数值变化如图4所示。在种群进化到10代时,函数值收敛到﹣0.005 4,位置为(0,0)。比较图3和图4可见,基本遗传算法出现早熟现象,陷入局部最优解,而基于遗传算法和非线性规划的函数寻优算法以较小的种群规模,进化到更好的解。基于遗传算法和非线性规划的函数寻优算法跳出了局部最优,在收敛结果和求解结果上都明显优于基本遗传算法。
5 结论
函数极值寻优现象是日常生活中比较常见的一类问题。本文结合非线性规划和遗传算法的各自优点,一方面采用遗传算法进行全局搜索,一方面采用非线性规划进行局部搜索,得到全局最优解,避免了遗传算法早熟,陷入局部最优解。实验分析结果充分表明,在处理复杂非线性函数极值寻优问题上,基于遗传算法和非线性规划的函数寻优算法具有明显的优势,需要种群规模小,收敛速度快,寻找到的极值非常接近最优解,为解决现实生活中的一些极值寻优问题提供了一种可借鉴的思路。
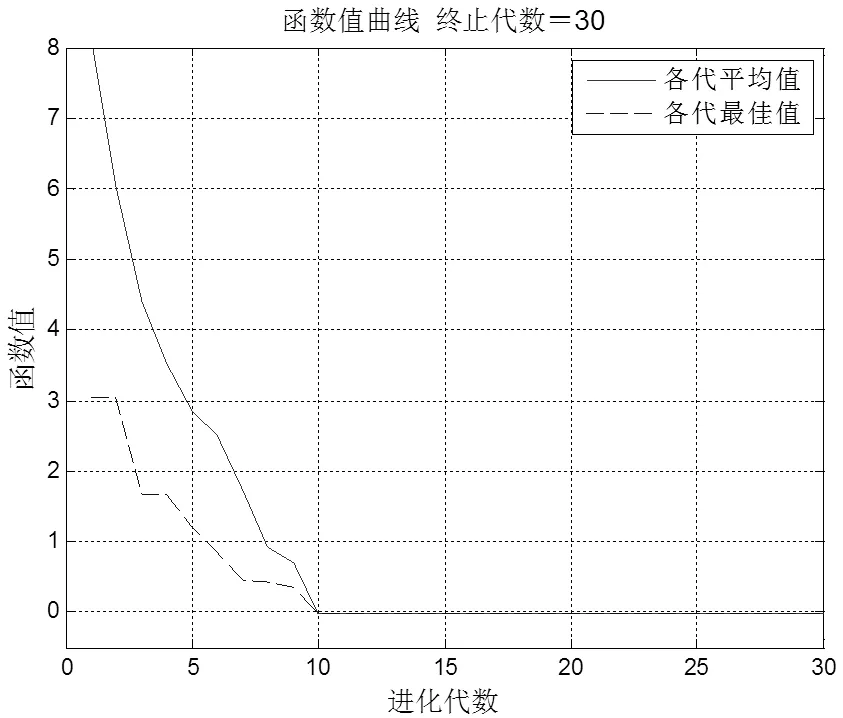
图4 非线性规划遗传算法优化过程
[1]李岩,袁弘宇,于佳乔,等.遗传算法在优化问题中的应用综述[J].山东工业技术,2019(12):180,242-243.
[2]吴龙,任红民,毕惟红.遗传算法求解非线性方程组研究综述[J].电子科技,2014,27(4):173-178.
[3]张国民.遗传算法的综述[J].科技视界,2013(9): 37,36.
[4]申合帅,李泽民.混合线性约束非线性最优化问题的一个新算法[J].湖南师范大学自然科学学报,2018,41(5):75-81.
[5]薛美芬,陈奕榕,陈省江.基于蒙特卡罗法与梯度法解非线性优化问题的研究[J].宁德师范学院学报(自然科学版),2017,29(2):127-130.
[6]杨娜,荆园园.基于改进PSO算法的函数极值寻优研究[J].计算机仿真,2015,32(9):263-266.
TP18
A
10.15913/j.cnki.kjycx.2019.15.016
2095-6835(2019)15-0047-02
〔编辑:王霞〕
