基于乡（镇、区）尺度的平原区农村居民点分形特征及布局优化研究

邢美玲 梁彦庆 黄志英

摘要：剖析平原区农村居民点的分布特征，合理确定农村居民点布局优化方向，可为新农村建设过程中平原区村庄整治和布局调整提供指导。应用分形理论，结合地理信息系统（GIS）空间分析和SPSS统计分析，以典型平原区河北省深州市为例，通过测算2009、2015年农村居民点集聚维数、Zipf维数、边界维数和稳定性指数，分析乡镇尺度下农村居民点的分形特征并提出农村居民点布局优化方案。结果表明，（1）全市农村居民点空间结构集聚效应显著，集聚维数达 1.165 5。（2）各乡镇农村居民点规模分布集中、分散几近各半，其中9个乡镇农村居民点Zipf维数下降，分布趋于集中;7个乡镇农村居民点Zipf维数上升，分布趋于分散;2乡镇Zipf维数基本不变，分布趋于均衡。（3）各乡镇农村居民点形态呈现复杂且不稳定趋势的占多数，其中11个乡镇农村居民点边界维数上升，稳定性指数下降，空间形态更复杂且呈扩张不稳定趋势;6个乡镇农村居民点与其相反;1个乡边界维数和稳定性指数未发生变化，空间形态相对稳定。（4）基于各乡镇农村居民点分形特征，提出了稳步城镇化型、快速城镇化型、加速集约化型和特色产业化型4种模式下的农村居民点布局优化方案。

关键词：农村居民点;分形维数;分形特征;布局优化;平原区

中图分类号：F321.1   文献标志码： A  文章编号：1002-1302（2019）12-0281-06

收稿日期：2018-03-05

农村居民点作为农村人地关系的核心，已成为农村土地利用的重中之重[1]，随着全国土地整治和新农村建设的加快，农村居民点用地集约利用成为土地整治工作的重要任务之一，而当前平原区农村居民点“满天星”、散落式的局面突出，在此背景下，准确把握平原区农村居民点演化的内在规律对农村居民点整理工作具有重要意义[2-4]。不同于传统视角了解事物本身特性[5]，分形理论通过事物内部相似性来研究事物整體特征，被广泛应用于城镇体系[6]、景区空间结构[7]、城市地价[8]等领域，而农村居民点自身拥有的相似性和不规则性也有学者通过分形理论进行研究，李玉华等通过分形理论分析重庆市4种生态类型农村居民点分形特征及其影响因素，结果发现，不同生态类型居民点特征不同且影响因素也不尽相同[9];宋志军等利用分形理论研究发现，北京近中郊、远郊、山区3个区域农村居民点空间演变与区域农业生产进程存在差异，并提出不同区域农村居民点规划和整理策略[10]。然而，对农村居民点分形特征的研究在研究类型、尺度及应用等方面仍需进一步探讨[9，11-13]。选取典型平原区河北省深州市为研究区域，基于乡（镇）尺度分析农村居民点分形特征，总结农村居民点内在发展规律并提出布局优化方案，以期为新农村建设过程中开展农村居民点整治工作提供科学依据。

1 研究区概况及研究方法

1.1 研究区概况

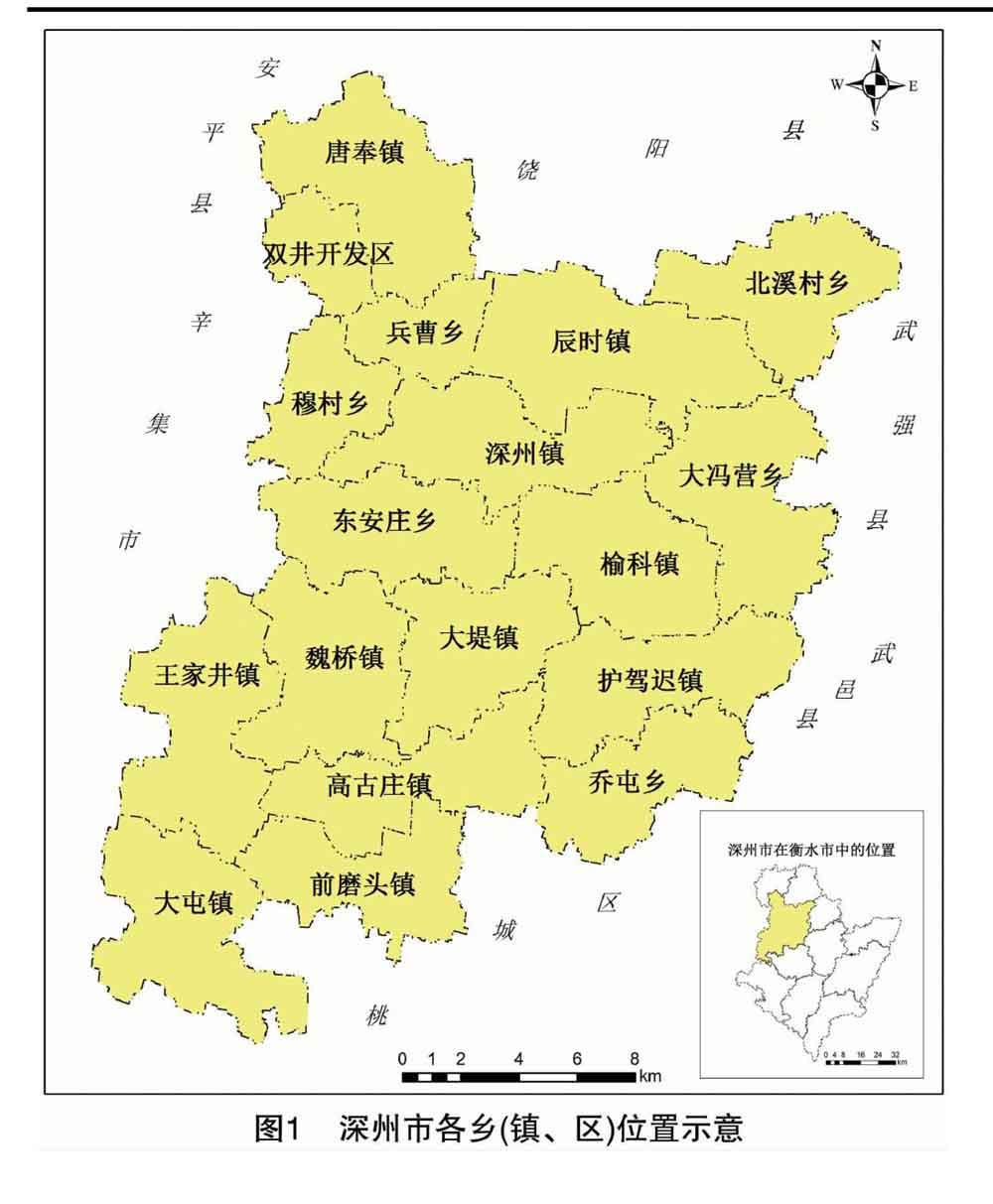
深州市位于河北省衡水市西北部，位于37°42′～38°11′N，115°21′～115°50′E之间，南距衡水市中心城区 30 km（图1），地处黑龙港流域，属典型低平原区，境内地势平坦开阔，由西南向东北微有倾斜，海拔最高处28.0 m、最低处17.5 m。辖区面积1 245 km2，现辖深州镇、魏桥镇、高古庄镇、东安庄乡、乔屯乡、兵曹乡、辰时镇、北溪村乡、穆村乡、唐奉镇、前磨头镇、大堤镇、大冯营乡、王家井镇、榆科镇、护驾迟镇、大屯镇、双井开发区等18个乡（镇、区），465 个行政村。全市以农业发展为主，是国家优质粮食、水果、花生产地。2009 年全市农村居民点用地13 767.50 hm2，占土地总面积的1106%;2015 年全市农村居民点用地13 923.21 hm2，占土地总面积的11.18%。

1.2 研究方法

分形维数是表示自相似性事物和现象的标量，是研究分形理论的重要工具[14]。在农村居民点分布中，分形维数数值反映其分形特征，维数值越高， 说明分布自相似性越高，居民

点分布越混乱。

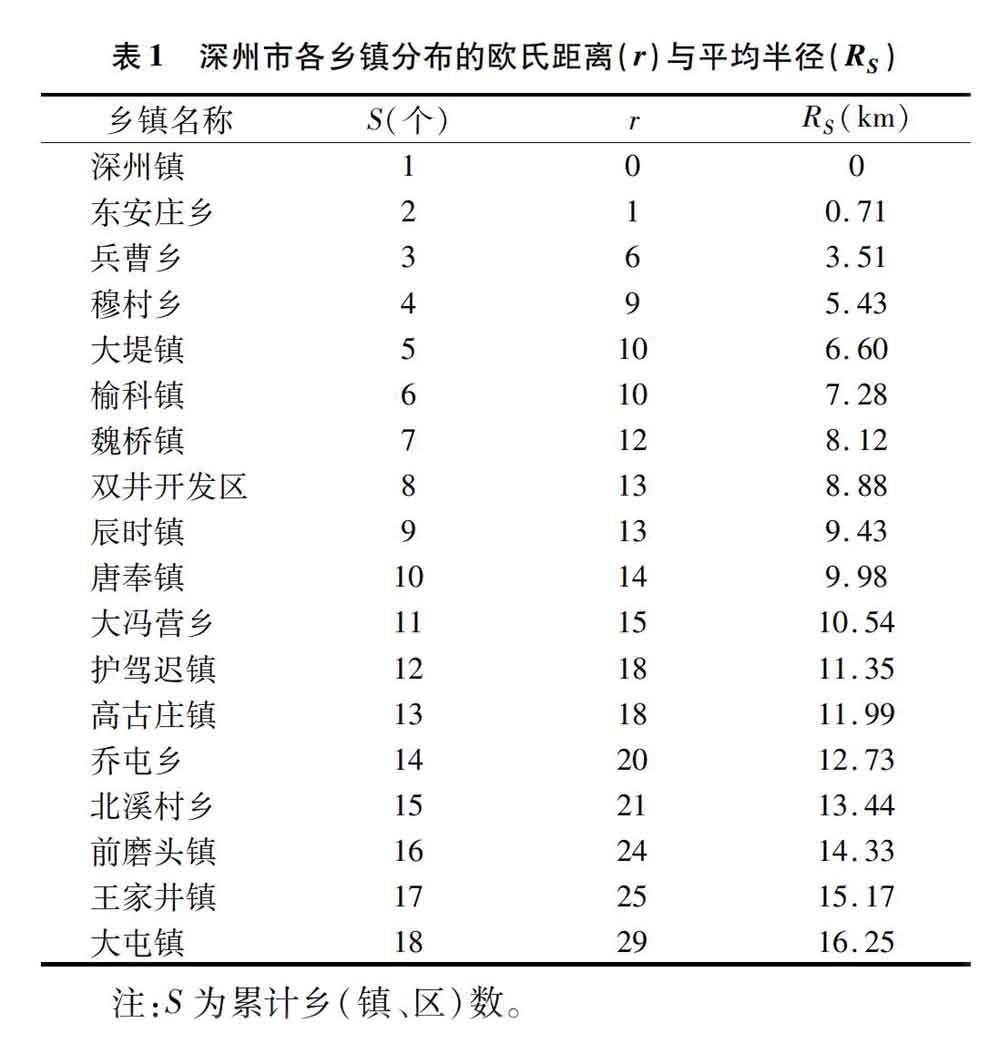
1.2.1 集聚维数 集聚维数反映全市农村居民点的空间结构分布格局和向心聚集程度。若半径为r的圆范围内有 N（r） 个居民点，则可确立r和N（r）间的关系，即有N（r）∝CrD，其中CrD表示半径为r的圆范围内的居民点数，由于半径r影响分维数值，可将其转化为平均半径，因而以居民点内最大城镇（中心城镇）为重心，可定义居民点随机空间分布的平均半径RS[15]，即式中：RS为平均半径;S为乡（镇）个数;ri为第i个乡（镇）到（中心城镇）的欧氏距离（也称重心距离，i=1，2，3，…，n）;<> 表示平均。根据居民点随机集聚的分形特征，如果在一定时空条件下，平均半径RS与城镇个数S间有如下关系：RS∝SE11 或者S∝RSE1，其中E1为分维数，说明中心城镇的吸引力呈现出分形的特征，可以对其进行双对数转化，得到如下公式：

式中：这里R0是一常数量，E是分维，其地理意义为各乡（镇、区）居民点围绕中心城镇随机集聚的特征，故E被称为集聚维数。

集聚维数E一般取维数2 为参考值，当集聚维数E<2时，各乡镇居民点的空间分布密度由中心向周围递减，说明中心城镇集聚效应较强;当E=2时，各乡镇居民点的空间分布较为均质;当E>2时，各乡镇居民点的空间分布密度由中心向周围递增，即中心城镇处在离心分离状态。

1.2.2 Zipf维数 Zipf维数反映农村居民点的空间分布规模性、均衡性。城镇和村委会驻地构成了镇域内村级规模以上的居民点体系。对居民点规模分布的研究可以利用Zipf公式：

式中：K为居民点序号（K=1，2，…，N，其中N为系统中居民点总数）;PK为序号为K的居民点人口;P1为中心镇人口数;q为Zipf指数，由于q具有分维意义，故称之为Zipf维数[16]，其与分维数F互为倒数，即F=1/q。对公式（3）取对数得：

通过公式（4）可以求出指数q，q的取值不同，意义也不同。当中心镇发展快于镇域内村级规模以上的居民点时，q增大，F减小，人口分布差异程度较大，中心镇垄断性较强，中间位序居民点较少，城镇体系发育不成熟，居民点规模分布比较分散;当镇域内中心镇发展慢于村级规模以上的居民点时，q减小，F增大，人口分布较均衡，中间位序居民点较多，城镇体系发育较成熟，居民点规模分布比较集中;当q→∞时，镇域内只有一个居民点;当q→0 时，所有居民点规模一样大，这2种极端情况实际上不存在。

1.2.3 边界维数 边界维数通过测算图斑周长和面积，描述农村居民点斑块边界的曲折性，从而反映图斑在空间上相互交错的形态性与空间渗透的复杂性[17-18]。Mandelbrot在传统欧式几何图形关系基础上，提出周长-面积关系[19]：

边界维数的理论范围为1～2，边界维数可以反映出图斑形状复杂程度及分布情况，维数越大，相同面积的周长越长，图斑越复杂，居民点分布越混乱无章[21]。当维数<1.5时，说明图形趋向于简单;当维数=1.5时，表示图形处于布朗随机运动状态，越接近于该值，稳定性越差;当维数>1.5时，则图形较为复杂。从时空角度讲，若维数随时间变化而增大，则说明该农村居民点形态演变复杂且不规则，在空间上呈现扩展趋势;反之，该农村居民点形态变的简单，在空间上呈现缩小趋势[21-22]。

1.2.4 稳定性指数 稳定性指数（SK）是指居民点在自然状态下抵御外来干扰、维持自身形态的能力。SK越大，表示居民点空间结构越稳定。当D=1.5的时候，居民点空间结构最不稳定[21，23-24]。

1.3 数据来源及处理

研究数据来源于深州市2009、2015 年土地利用变更调查成果和《深州市统计年鉴》。将统计年鉴中各乡镇及村的人口数以及土地利用变更成果中地类名称为村庄的地类图斑纳入农村居民点图层，图层属性信息包括地類、权属、周长、面积、人口等，经处理统计得到图斑个数、图斑总面积和周长、图斑平均面积及平均周长等数据。

分形处理步骤，以市政府所在地深州镇为集聚分形的中心点，运用ArcGIS 10.0软件根据土地利用变更数据库测得各乡镇空间位置信息，建立起深州市地域系统的空间属性数据库，通过分别测算各乡镇至中心点的距离，根据公式（1）、公式（2）求取集聚维数E;将各乡镇村人口数由大到小排列，按其位序与各自规模分别取对数后，进行线性回归分析，得到Zipf维数q;利用ArcGIS10.0 软件对所有地类属性为村庄的图斑进行量算，获得图斑周长、面积，计算得到lnP、lnA，利用SPSS软件进行回归分析得到曲线拟合方程，进而根据公式（7）、公式（8）得出边界维数D及稳定性指数SK。

2 结果与分析

2.1 农村居民点规模结构分形特征

2.1.1 全市空间结构分形特征 以深州市全市为研究对象，结合各乡镇到中心城镇（深州镇）的欧氏距离，借助公式（1）得出平均半径RS（表1），并应用公式（2）对其进行回归模拟，得到lnRS=0.858lnr+1.054，E=1/0.858=1.1655<2，R2=0.959。

由模拟方程可知，全市居民点随机集聚维数E=1.165 5<2，R2=0.959﹥0.95 ，总体拟合情况较好，具有明显的分形几何特征，表明深州全市居民点围绕中心城镇（深州镇）呈集聚状态分布，集聚效应显著，具体表现为从中心城镇向四周呈递减的空间分布特征，即中心城镇在全市居民点中处于垄断地位，对周围城镇的吸引和辐射作用显著，越向四周，吸引力减弱的速度越快[25]。

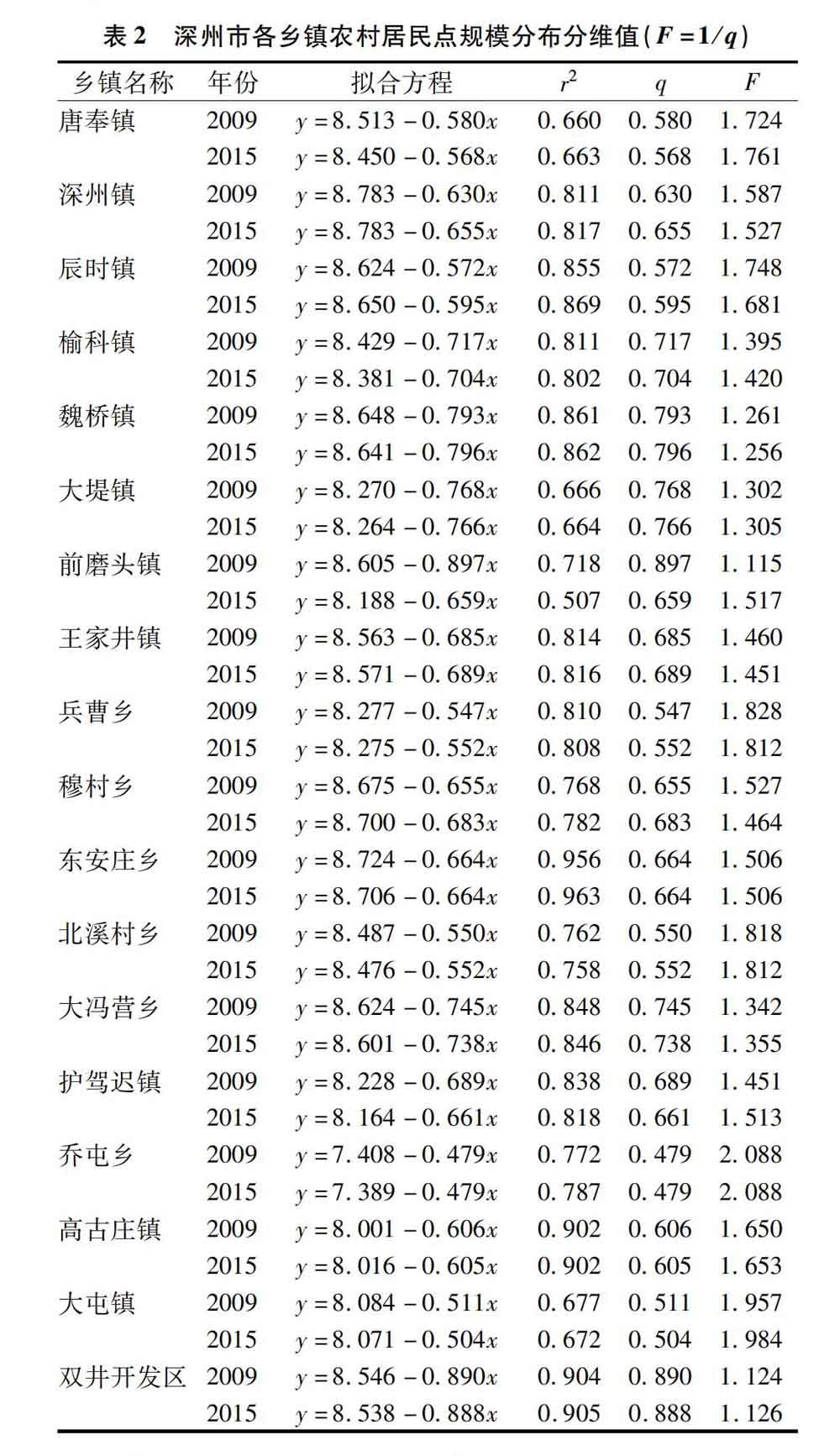
2.1.2 各乡镇规模分布分形特征及对比 以深州市18个乡镇组成的乡镇体系为研究对象，结合各乡镇所辖村的实际人口数量，按照公式（3），应用公式（4），得出2009年和2015年各乡镇农村居民点规模分布的拟合方程、r2值、q值（表2）。

表2中r2值较大，说明拟合效果较好。通过分析q与F的变化得出以下结论：通过Zipf维数可知，深州市2009、2015年各乡镇农村居民点规模分布呈现趋于分散、集中几近各半的特征。其中，深州镇、辰时镇、兵曹乡、北溪村乡、王家井镇、魏桥镇、穆村乡等呈现q上升、F下降趋势，表明这些乡镇随时间推移各自中心镇发展较快，其居民点规模分布趋于分散;唐奉镇、榆科镇、大堤镇、前磨头镇、护驾迟镇、高古庄镇、大冯营乡、大屯镇、双井开发区等9乡镇（区）呈现q下降、F上升趋势，表明这些乡镇居民点发展较快，规模分布趋于集中;东安庄乡、乔屯乡q值无变化，表明2个乡居民点发展较均衡（图2）。

2.2 农村居民点空间形态分形特征

2.2.1 深州市空间形态分形特征 经过对图斑处理与统计得到全市农村居民点相关指标数据，经由公式（5）～公式（7）计算得到全市居民点2009年和2015年面积-周长对数拟合方程和相关检验值。

从表3可以看出，2015年与2009年相比，全市图斑总个数增加168个，总周长增加82.27 km，总面积增加 155.71 hm2，平均周长减少44.44 m，平均面积减少 0.67 hm2。表明近6年全市居民点的数量和总规模呈现递增态势，而个体平均规模呈现递减态势。

2009年和2015年分形结构模型的R2分别为0.982和0978，达到极显著水平，表明全市农村居民点存在分形特征，边界维数（D）分别为1.068和1.146，稳定性指数（SK）分别为0.432和0.354。由此可知，经过6年的发展，农村居民点边界维数有所增加，稳定性指数有所降低，总体上全市农村居民点布局趋于复杂和不合理，农村居民点扩建的随意性增大。

2.2.2 各乡镇空间形态分形特征及对比 经过对图斑处理、统计与测算，得到各乡镇农村居民点2009、2015年面积-周长对数拟合方程和相关检验值。

从表4、图3可以看出，（1）唐奉镇、深州镇、辰时镇、榆科镇、王家井镇、魏桥镇、兵曹乡、东安庄乡、北溪村乡、大冯营乡、双井开发区等11个乡镇（区）的D呈现上升趋势，SK有所下降，表明居民点分布趋向于复杂不规则和不稳定，与全市居民点布局整体趋势相吻合。（2）前磨头镇、护驾迟镇、乔屯乡、高古庄镇、大屯镇、大堤镇等的D小幅降低，SK有所上升，表明居民点分布相对规则、稳定，呈复杂性下降、稳定性上升趋势，与全村居民点布局整体趋势相反。（3）穆村乡的D、SK值未出现变化，表明居民点分布稳定，变动较小。

结合乡镇区位分布可以总结得出，农村居民点分布规则与稳定性在一定程度上与各乡镇距衡水市城区距离有关。农村居民点分布趋向于复杂不规则和不稳定的11个乡镇主要位于深州市北部，距离衡水市城区较远;农村居民点分布相对规则、稳定的6个乡（镇）位于深州市南部，与衡水经济技术开发区、桃城经济开发区相邻，受衡水市城区辐射影响较大;而穆村乡作为深州市特色蜜桃产区，农业产业化程度较高，区域内土地利用方式较稳定，外来影响因素较小，农村居民点分布稳定。

2.3 深州市农村居民点优化布局

基于“2.2”节中分析得出的分形维数，按其变化将农村居民点分形特征分为集中且稳定、均衡且稳定、集中且不稳定、均衡且不稳定、分散且不稳定、分散且无显著变化等6种（表5）。2009—2015年，农村居民点分形特征表现为集中且稳定的乡镇有5个，分别为前磨头镇、护驾迟镇、高古庄镇、大堤镇、大屯镇，其Zipf维数下降，边界维数下降，稳定性指数上升;均衡且稳定的仅有乔屯乡，其Zipf维数不变，边界维数下降，稳定性指数上升;集中且不稳定的有4个乡镇，分别为唐奉镇、榆科镇、大冯营乡、双井开发区，其Zipf维数下降，边界维数上升，稳定性指数下降;均衡且不稳定的仅有东安庄乡，其Zipf维数不变，边界维数上升，稳定性指数下降;分散且不稳定的有6个乡镇，分别为深州镇、魏桥镇、辰时镇、王家井镇、兵曹乡、北溪村乡，其Zipf维数上升，边界维数上升，稳定性指数下降;分散且无显著变化的仅有穆村乡，其Zipf维数上升，边界维数和稳定性指数不变。

依据居民点分形特征，结合深州市实际，将农村居民点布局优化模式分为4种类型（表6、图4），将集中且稳定、均衡且稳定的分形特征归纳为稳步城镇化型，集中且不稳定、均衡且不稳定的分形特征归纳为快速城镇化型，分散且不稳定的分形特征确定为加速集约化型，分散且无显著变化的分形特征确定为特色产业化型。

2.3.1 稳步城镇化型 主要涉及前磨头镇、护驾迟镇、高古庄镇、大屯镇、大堤镇、乔屯乡6个乡（镇）。这些乡镇主要分布在衡水市主城区边缘，受衡水市影响较大，尤其是前磨头镇拥有前磨头火车站，交通便捷，农村经济发展水平相对较高，基础设施较完善。未来可依托衡水市主城区的核心带动作用，加快农村产业发展，强化综合交通运输网络支撑，加强相关配套设施建设，推进城乡统筹发展。

2.3.2 快速城镇化型 主要涉及唐奉镇、榆科镇、大冯营乡、双井开发区、东安庄乡5个乡镇。农村居民点快速城镇化随城乡间交流和联系的不断深入而加快，由此造成城镇与乡村间的功能分工愈加广泛和深刻，进而推动城镇和乡村在工业化和城镇化进程中不可避免的变动和转型[26-28]。榆科镇、大冯营乡、东安庄乡紧邻深州镇，农村居民点发展可依托中心城镇的带动优势和区内黄石高速、307国道及大广高速的交通优势;唐奉镇和双井开发区紧邻安平县全国最大丝网基地，农村居民点可借助丝网产业辐射影响加快农村产业经济和产业结构调整。由于不稳定的分形特征，这些乡镇应结合紧邻中心城镇区位、交通及相邻产业的优势，通过转型发展，强化乡镇间的交通联系，实现农村社会经济的快速发展，同时新建居民点要在基础设施等级相对较高的区位进行选址。这种优化模式是深州市未来农村居民点发展的重点。

2.3.3 加速集约化型 主要涉及深州镇、魏桥镇、辰时镇、王家井镇、兵曹乡、北溪村乡6个乡（镇）。由于分散且不稳定的分形特征，这些乡镇需通过拆村并点等方式进行村庄并组整合，实质是实现农村社会资源合理配置[29-30]。这些乡镇受衡水市影响相对较小，近年来农村居民点发展相对无序，因此，这些乡镇可采取适当政策和限制发展措施，推动住宅腾空与用地置换，逐步减小居民点用地规模，减少废弃、闲置、低效用地，消除杂乱无序的布局现状，通过整理将居民点集中布置，为农业的机械化和产业化发展创造条件，实现农村居民点加速集约化。这种优化模式具有突出重点、层次结构明显、集约效应显著的特点。

2.3.4 特色产业化型 特色产业化型仅涉及穆村乡，该乡是深州市特色蜜桃产区，农业产业化程度较高，基于其近年来呈现出的分散且无显著变化的分形特征，在发展特色农业的基础上，可集中发展部分特色农业基地村、旅游村，通过提高农业综合生产能力，打造特色优势品牌，提高市场竞争力，推动现代农业建设步伐，为现代农业的规模化、集约化生产经营管理创造良好的条件，保障农村居民点的特色有序发展。

3 讨论与结论

深州市农村居民点规模结构分形特征显著，利用集聚、Zipf维数能有效地表征其规则分布性。从全市看，以乡镇为统计单元的全市农村居民点空间结构呈现以深州镇为辐射中心向四周衰减，空间结构呈现聚合发展的态势。但从乡镇尺度看，以村为统计单元的各乡镇由于地理位置、交通与社会经济水平差异，辰时镇、兵曹乡等乡镇内部规模分布相对分散。因此需要通过加强交通等基础设施的建设，形成农村居民点间交通网络化，以促进结构优化。

深州市农村居民点空间形态分形特征显著，利用边界维数能有效地表征其复杂性。从全市看，农村居民点空间形态特征日趋复杂，稳定性越来越低，发展的随意性越来越大。从乡镇尺度看，深州镇和王家井镇等乡（镇、区）农村居民点形态趋向复杂且不稳定。究其原因，主要是因为城镇化速度加快，在一定程度上影响了农村居民点布局。因此在加快深州市城镇化的发展过程中，要科学编制土地利用規划，优化农村居民点用地布局，降低其农村居民点扩建的随意性，保障农村居民点空间资源的合理配置，实现深州市农村居民点可持续发展。

本研究分形与优化研究定位于乡（镇）微观尺度，并通过利用3种不同分形维数对深州市农村居民点结构与形态特征进行刻画，综合分析动态变化及其自组织演化规律，研究结果可为农村居民点新建、农村居民点选址和用地综合整治等方面提供参考。针对基于分形特征归纳的农村居民点优化布局模式，后续可因地制宜地进一步探索居民点优化布局方案。

按照本研究结果中的趋势可以推断，深州市农村居民点在全市层面上分布将更集中，但在乡镇层面上空间结构与形态发展差异仍较大。结合庄至凤等运用关联维数进行分乡镇结构、规模特征[31]的探讨，今后可加强对影响各乡镇居民点关联要素特征的分析，以更有针对地对分乡镇居民点布局优化进行指导。

本研究對平原区河北省深州市农村居民点分形特征进行了分析，并基于分形特征提出了农村居民点优化布局模式。主要研究结论如下：（1）全市农村居民点E达1.165 5，农村居民点集聚效应显著，围绕深州镇呈集聚状态。（2）2009年以来，唐奉镇、榆科镇等9乡镇q下降、F上升，这些乡镇居民点发展较快，规模分布趋于集中;深州镇、辰时镇等7个乡镇q上升、F下降，这些乡镇随时间推移各自中心镇发展较快，其居民点规模分布趋于分散;乔屯乡、东安庄乡等2个乡q值不变，2个乡居民点发展较均衡。（3）全市2009、2015年农村居民点D为1.068、1146，SK为0.432、0.354，D上升、SK下降，表明全市农村居民点分布趋向于复杂和不合理。唐奉镇、深州镇等11个乡镇D上升、SK下降，农村居民点分布趋向于复杂和不合理;相反前磨头镇、护驾迟镇等6个乡镇D下降、SK上升，农村居民点分布趋向于规则和稳定;穆村乡D无变化，居民点分布相对稳定。（4）全市农村居民点布局优化模式归纳为稳步城镇化型、快速城镇化型、加速集约化型、特色产业化型4种类型。提出密切依托衡水主城区的带动作用，加强稳步城镇化型区域的相关配套设施建设;充分挖掘快速城镇化型区域紧邻中心城镇区位、交通及相邻产业的潜力优势，通过转型发展，加强乡镇之间联系;根据相关政策，通过拆村并点等方式进行村庄并组整合，逐步减小居民点用地规模，减少废弃、闲置、低效用地，消除杂乱无序的布局现状，加速集约化型区域集中布置;应结合有关规划，保障特色产业化型区域特色农业基地村集中有序发展。

参考文献：

[1]孔雪松，金璐璐，郄 昱，等. 基于点轴理论的农村居民点布局优化[J]. 农业工程学报，2014，30（8）：192-200.

[2]姜广辉，张凤荣，秦 静，等. 北京山区农村居民点分布变化及其与环境的关系[J]. 农业工程学报，2006，22（11）：85-92.

[3]李 鑫，甘志伍，欧名豪，等. 农村居民点整理潜力测算与布局优化研究——以江苏省江都市为例[J]. 地理科学，2013，33（2）：150-156.

[4]姜广辉，张凤荣，陈军伟，等. 基于Logistic回归模型的北京山区农村居民点变化的驱动力分析[J]. 农业工程学报，2007，23（5）：81-87.

[5]朱晓华. 地理空间信息的分形与分维[M]. 北京：测绘出版社，2007：3-20.

[6]吕祯婷，焦华富. 基于分形理论的安徽省城市体系规模分布研究[J]. 世界地理研究，2008，17（3）：107-112.

[7]胡章鸿，段七零. 基于时空距离的江苏省景区系统聚集分形演化研究[J]. 长江流域资源与环境，2014，23（9）：1208-1214.

[8]杨奎奇，汪应宏，张绍良，等. 城市地价分形特征与测算方法研究[J]. 中国矿业大学学报，2012，41（4）：686-690.

[9]李玉华，高 明，吕 煊，等. 重庆市农村居民点分形特征及影响因素分析[J]. 农业工程学报，2014，30（12）：225-232.

[10]宋志军，关小克，朱战强. 北京农村居民点的空间分形特征及复杂性[J]. 地理科学，2013，33（1）：52-60.

[11]车明亮，聂宜民，姜曙千，等. 平邑山区农村居民点分形特征及影响因素[J]. 农业工程学报，2010，26（增刊2）：360-365.

[12]陈伟强，霍明明，马月红，等. 农村居民点空间分布特征及演变研究[J]. 河南农业大学学报，2014，48（3）：354-358.

[13]余万军，吴次芳，关 涛，等. 基于GIS和分形理论的山西屯留县土地利用空间格局变化[J].农业工程学报，2005，21（10）：64-69.

[14]Mandelbrot B.How long is the coast of Britain？ Statistical self-similarity and fractional dimension[J].Science，1967，156（3775）：636-638。

[15]闫广华.基于分形理论的长春都市圈城镇体系结构测度及其优化研究[J]. 长春教育学院学报，2016，32（12）：41-45.

[16]徐 亮，胡海霞，郑 黎.元通镇居民点规模布局的分形研究与规划[J]. 经济地理，2001，21（增刊1）：150-153.