基于随机-关联空间插值法的工程岩体力学参数确定
2019-08-21
(1.西南石油大学 土木工程与建筑学院,成都 610500;2.泸州市泸县 住建局,四川 泸州 646000;3.西南交通大学 交通运输与物流学院,成都 610031)
1 研究背景
工程岩体力学参数的合理取值,是工程岩体稳定性分析的关键步骤, 也是多年来岩体力学界存在的一大难题[1-2]。 在取值过程中, 主观上受到采样扰动、 试验方法、 随机量测误差带来的影响; 客观上, 在复杂的赋存环境、 地质作用、 岩体成因、 地质作用等多种因素的共同作用下, 岩体的力学参数在空间上存在随机不确定性和结构关联性[3-4]。 因此,在工程岩体力学的设计取值中, 需要选择合适的试验方法, 同时也必须考虑工程岩体力学参数在在空间上的不确定性和结构关联性这一客观实际问题。
工程岩体力学参数的随机不确定性是指岩体力学参数的数值呈现随机分布且变化各异,这是由不同影响因素综合作用而成的,如:岩体自身的矿物组成,岩体赋存环境的围压大小、固结历史、形成年代,岩体在形成过程中受到构造运动、风化作用、溶蚀、卸荷作用的往复改造;内外动力地质的耦合作用使得岩石具有天然变异性,同时导致岩体结构面随机分布,使得岩体力学参数在数值上表现出随机分布的特点[5-9]。由于岩体力学参数的随机性和空间变异产生的主导因素可能不同,相应地,用于预测岩体力学参数的方法也应具有针对性。
针对工程岩体自身的天然变异性引起的力学参数随机性,文献[10]—文献[12]利用统计学的方法,以一定的概率模型来描述岩体力学参数的分布类型及其特征。针对岩体结构面随机分布引起的力学参数随机性,文献[13]和文献[14]根据节理几何参数模型,利用Monte-Carlo方法模拟不同尺寸岩体试件;文献[15]通过“随机-确定”耦合模型,模拟了离散裂隙随机网络模型中的结构面分布特征。统计学方法大多以岩体力学参数分布符合某种已知的概率分布模型为前提条件对其进行描述;但由于岩体天然变异性及结构面的随机分布,难以得到其概率分布函数,其真实的概率分布函数可能不符合现有的分布模型。利用计算机技术进行数值模拟,在建模和赋值时往往带有较强的个人主观性,不能客观反映现场实际。
同时,岩体力学参数并不是一般意义上的纯随机变量,而是同时具有局部随机性和整体关联性。工程岩体力学参数的关联性是指岩体在形成和后期改造过程中受到各种宏观规律控制,岩体结构面之间相互关联,这使得空间中不同位置的岩体力学参数之间也存在某种程度的关联。针对岩体力学参数关联性的特点,文献[16]考虑了一定范围内岩体力学参数的波动范围和相关距离的关系,文献[17]和文献[18]结合有限元的中心点离散法和局部平均离散法研究了岩土力学参数变化特征。上述研究多以样本点为中心,对周围岩体的力学参数变化特征和波动范围进行研究,但对样本点之间的关联性缺乏考虑;同时,由于样本携带的信息量有限,在样本信息较少的情况下,难以对整个工程场地中的岩体力学参数作出符合客观实际的评价。
目前对于工程岩体力学参数的随机性和关联性已经进行了一定程度的研究,但在概率分布函数未知、样本信息较少的情况下得到的工程岩体力学参数估值并不理想。为了解决工程岩体力学参数的随机性导致其概率分布未知的问题,以地质统计学中区域化变量理论考虑岩体力学参数,利用样本矩替换母体矩,通过变差函数建立岩体力学参数的空间分布模型;为了考虑样本点之间、样本点与插值点的岩体力学参数的关联性,利用变差函数对其进行定量描述;采用克里格法对样本点之间的工程岩体力学参数进行空间插值。通过工程实例,分析该方法的适用性和应用范围,选取不同数量的样本进行插值对比。对比结果表明该方法对样本数量具有依赖性。
2 空间分布模型的建立
对岩体样本进行预处理后,基于地质统计学中区域化变量理论构造试验变差函数,并与理论变差模型进行拟合及交叉验证后得到满足条件的空间分布模型。
2.1 构造试验变差函数
区域化变量是指一定空间范围内具有某种关联性的随机变量[19-20]。岩体在形成过程中受地质作用的影响,使其在空间中具有结构和组成成分上的关联性以及随机不确定的变异性,将岩体力学参数作为区域化变量进行研究,有助于了解其关联性和随机性2个客观存在的基本属性,并通过变差函数对其进行定量分析。将工程岩体力学参数记为Z(xi),表示工程岩层中多个空间点i的岩体力学参数取值,其中i的取值为1,2,…,k。
实际工程中构造该场地中区域化变量的试验变差函数时,需要从方向和距离2个方面对工程岩体力学参数样本数据进行综合考虑,如图1所示。图中,Z(x0)为x0点的岩体力学参数;h为基于各空间点的相对距离选择的合理滞后距;kh为k点与滞后距h的乘积;ε(h)为距离误差限。

图1 综合考虑方向和距离的数据模型Fig.1 Data model in consideration of directionand distance
将数据组合成角度组,也就是说在(α-dα,α+dα)方向范围内的岩体力学参数空间点都看成α方向的数据点(设α方向的角度允许误差为dα),其中dα一般取两相邻方向夹角的1/4,最大不超过两相邻方向夹角的1/2;再将数据按距离[kh-ε(h),kh+ε(h)]组合起来。这样,凡是落在角度范围(α-dα,α+dα)及距离范围[kh-ε(h),kh+ε(h)]内(图1阴影部分)的岩体力学参数空间点都认为是x0点在其中α方向上相距为kh的数据点[18]。
基于各空间点的相对距离选择合理的滞后距h,按照式(1)计算出不同滞后距对应的试验变差值。
(1)
式中:dij是为了使两空间点的距离接近kh选择的权系数,dij=1-[hj-kh/ε(h)]2,其中k为空间点数;hj为某点与点xi在空间中的实际距离,且满足kh-ε(h) 利用加权多项式回归算法以及人工补偿的方式将试验变差函数与理论分布模型进行拟合后得到能够定量描述一定空间范围内的工程岩体力学参数随机性和关联性的空间分布结构模型。 文献[21]指出理论变差函数模型中的球状模型在确定工程力学岩体参数上具有较好的应用,其一般表达式为 式中:a为变程,表示工程岩体力学参数关联性的影响范围;C为拱高,表示工程岩体力学参数空间结构变化的极大值;C0为块金值常数,表示工程岩体力学参数在形成过程、宏观地质作用中导致的随机不确定性成分;C0+C为基台值,表示工程岩体力学参数在一定方向上总的空间变异幅度。 考虑到岩体具有各向异性的特点,需要对不同方向上的试验变差函数格局用式(3)进行结构套合。 (3) 确定了工程岩体强度参数的理论变差函数模型后,再利用交叉验证法对模型进行最优性检查;最终建立能够反映岩体强度参数空间分布特征的空间分布结构模型γ(h)。 根据一定范围内的样本点对某一插值点的区域化变量进行空间插值。由于工程岩体力学参数具有随机性和关联性,一定范围内任意一点的力学参数都受到该范围内所有点的力学参数的共同影响,其影响程度需要从方向和距离2方面进行考虑。在线性、无偏和方差最小的条件下确定出各已知空间点xi的岩体力学参数相对于未知点w的岩体力学参数的权系数λiw。 Zw满足无偏性的条件为 (4) 岩体力学参数估计方差的计算公式为 (5) 在无偏条件下,采用拉格朗日乘数法,使空间岩体力学参数的估计方差σ2最小,则有 (6) 协方差函数与变差函数的关系为 C(h)=C(0)-γ(h) 。 (7) 式中:C(h)为一个点与另一个点距离为滞后距h时的协方差函数;C(0)为一个点与自身的协方差函数,由于是同一个点,因而滞后距为0。 利用式(7)整理得到可用变差函数γ(h)表示的普通克里格方程组与普通克里格方差,分别为 (8) (9) 其矩阵表达式为 Kλ=M。 (10) 其中: (11) 基于二阶平稳假设条件下,通过方程组(式(11))可以得出各样本点对插值点的权重系数λiw。二阶平稳假设是指当区域化变量应满足下列2个条件:①区域化变量在整个研究范围内的数学期望存在且等于常数;②区域化变量在整个研究范围内的协方差函数存在且相同。因此,在岩性相对均一、没有显著的构造形迹和不同的岩体结构分区的区域内利用上述公式确定权重系数进行插值是适用的。当研究范围内出现特异值或岩体各向异性时,权重系数可以采用指示克里格或泛克里格方法进行确定;当研究范围内具有不同工程地质单元分区时,应根据实际情况分别建立相对应的变差函数,在分区交界处选择合适的方法,共同确定该区域中的岩体力学参数。 根据克里格方程得到各样本点的权重系数后,利用式(12)对待估点进行插值,即 (12) 实际工程为四川省成都市某高层建筑基坑工程。基坑开挖尺寸约为211 m ×167 m × 40 m(长×宽×高),地层分布倾向平缓,建筑持力层为中风化红层泥岩,为了确定该基坑中持力层(地下35~40 m处)的红层泥岩单轴抗压强度,对该区域进行了勘察取样。 钻孔位置平面分布图如图2所示,根据样本信息统计结果(表1)可知,该区域内样本点岩体力学参数变化平稳,无异常突变,可以使用本文所提出的方法对工程场地岩体力学参数进行插值。 图2 钻孔位置平面分布Fig.2 Layout of drilling holes 空间点坐标值/mxyz单轴抗压强度/MPaA142.3178.539.24.75B0.061.438.04.54C26.370.837.93.65D102.145.937.53.82E129.888.538.23.79F161.797.536.14.41G78.810.038.73.89H24.599.039.64.54I129.6135.737.83.49 图3 不同样本数量的变差函数Fig.3 Variation functions of tests with different sample number 考虑到有效样本数量会对估值结果产生影响(图3),为了分析有效样本数量对估值结果的敏感性问题,采用5个点、7个点、9个点钻孔的样本试验值分别选取适当的滞后距h1=44 m,h2=31 m,h3=22 m,距离误差限ε(h)=11 m,角度允许误差dα=7.5°~15°。由正东方向自西偏北30°方向分别作出6个方向的试验变差函数γ*(h1),γ*(h2) ,γ*(h3),并按照加权多项式回归法进行拟合;再通过试验变差函数γ(h1),γ(h2) ,γ(h3)分别建立克里格方程对待估点w1,w2,w3的单轴抗压强度进行插值,并与试验数据进行对比分析(表2和表3)。 图4 未知点区域化变量位置网图Fig.4 Network of regional variable of unknown location 待估点号估值结果/MPa5个样本点7个样本点9个样本点室内试验结果/MPaw14.634.484.064.24w24.424.263.864.04w34.674.584.044.27 表3 不同样本估值与试验结果相对误差Table 3 Relative error between estimation results withdifferent effective samples and test results 根据上述计算结果进行分析,结果表明:本文所提出的的随机-关联空间插值法在岩性相对均一、没有明显突变情况下,利用一定数量的样本可以建立岩体力学参数的变差函数对工程岩体的单轴抗压强度进行估值。估值结果与试验结果的相对误差受有效样本数量的影响,随着有效样本数量的增多,其相对误差相应地减小。其中,有效样本数量为5个与7个时选择的滞后距h相对较大,建立的变差函数没有准确反映岩体力学参数在一段区域内先减小又增大的变化情况;当有效样本数量为9个时选择的滞后距h相对较小,建立的变差函数更能准确反映岩体力学参数在空间中的变化情况。因此,实际工程中应根据工程场地的地质条件情况和场地范围大小选择合适的插值方法和有效样本数量进行插值计算。 由有效样本数量对估值结果的敏感性分析可知,有效样本数量的增多会减小估计值与试验值的相对误差。结合工程实际情况选择9个已知有效样本点对未知区域的40个空间点的单轴抗压强度进行空间插值,根据插值结果将场地划分为8个网格区域(图5),再根据区域中已知点与插值点共同确定出该区域的单轴抗压强度设计建议值(图6)。 图5 区域场地位置平面图Fig.5 Layout of regional sites 区域设计建议值/MPa区域设计建议值/MPaN14.25N54.20N24.00N64.10N34.17N74.08N43.98N84.37 为了解决工程岩体力学参数在空间中的随机性和关联性引起的工程岩体力学参数设计取值问题,提出随机-关联空间插值法,利用现场有限的样本信息,统计工程岩体力学参数空间分布的结构特征,对取样点之间的工程岩体力学参数进行空间插值,通过工程实例进行分析得到以下结论: (1)从实际出发,在概率分布未知的情况下,利用样本矩替换母体矩,建立反映场地中岩体力学参数的空间概率分布模型。 (2)将岩体力学参数作为区域化变量,利用有限的样本数据,通过变差函数定量描述取样点之间、取样点与插值点之间岩体力学参数的关联性,得到不同取样点对插值点的影响权重λi。 (3)该方法同时考虑了工程岩体力学参数具有随机性和关联性的二重特性,对于岩性相对均一,没有显著的构造形迹和显著不同的岩体结构分区的区域具有较好的适用性;对于存在不同工程地质单元分区或者岩体力学参数发生突变的情况,可以在此基础上使用泛克里格法或者指示克里格法进行估值。 (4)本文提出的方法对于有效样本的数量存在一定的依赖性,随着有效样本的增多,估值结果与试验结果的相对误差相应减小。在工程实例中,有效样本数量为9个,利用该方法获得的工程岩体力学参数指标与实际工程对比相对误差分别为4.2%,4.4%,5.3%,得到的岩体力学参数可以作为工程设计取值的重要依据。本文提出的方法在一定程度上优化了工程岩体力学参数合理取值的问题。2.2 空间分布模型的拟合
3 工程岩体力学参数的空间插值


4 工程实例
4.1 工程概况

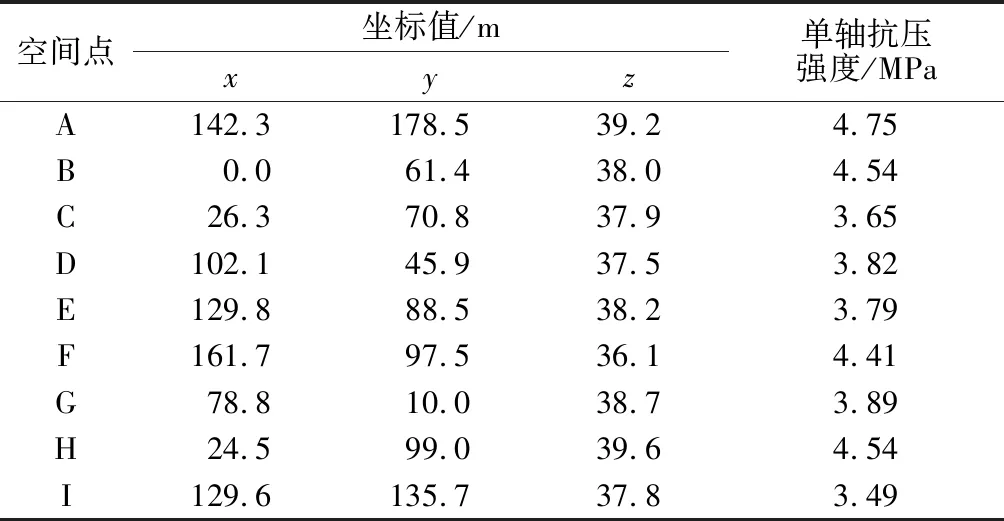

4.2 样本数量敏感性分析


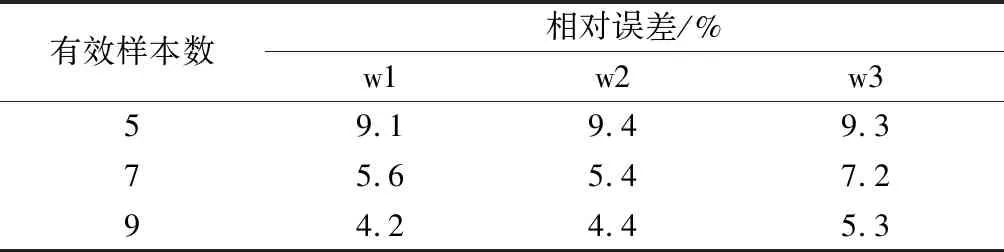
4.3 应用实例
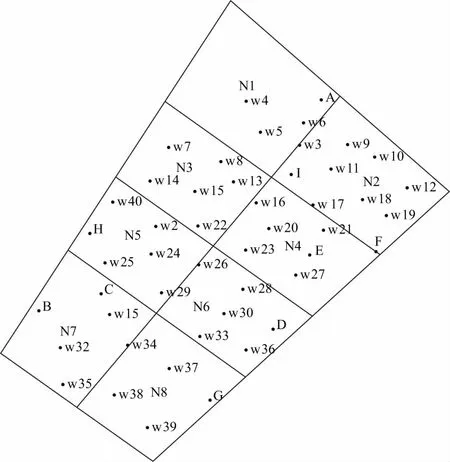

5 结 论
