城市轨道交通高架线路噪声预测简化模型的建立及验证

王 晨

(中铁上海设计院集团有限公司，200070，上海//高级工程师)

0 引言

城市轨道交通高架线路噪声的预测和防治已成为改善城市环境质量的重点，噪声预测则是所有防治工作的前提。目前，常用的城市轨道交通高架线路噪声预测方法有数理统计法、试验模拟法、模式计算(数学模型)法，以及空间信息软件与传统方法相结合的方法,其中,模式计算方法应用最为广泛。模式计算方法又分为偶极子模型、有限元模型、边界元模型等。

在轨道交通噪声预测中，使用最多的是HJ 2.1—2011《环境影响评价技术导则 总纲》的推荐模型。该模型将列车运行时的噪声源视为不相干的有限长偶极子线声源，以轮轨噪声为主要声源，并考虑传播过程中的各种衰减。由于考虑的因素较多，因此该模型的预测误差较大。在进行城市轨道交通高架线路噪声预测时，为简化该模型的计算量，仅简单地给出“相对于地面噪声高7～10 dB”假设，修正方法过于简单。文献[2-3]将列车看成一个移动的均匀线声源，采用单、偶极子传播模型来拟合轻轨列车的通过噪声，建立了适用于城市轨道交通高架线路噪声辐射的预测模型，但该模型比较简单，也未细分噪声不同来源的贡献程度。

利用有限元和边界元预测方法可极大提高计算结果精度。文献[4]针对有限元方法在高架桥梁振动和噪声预测方面的不足，建立铁路高架桥梁振动和噪声辐射的快速计算模型，得到了与实际试验相一致的数据。文献[5]将边界元Helmholtz积分公式和有限元流固耦合系统理论相结合，推导出了结构振动加速度与辐射声压之间的声传递向量，用以预测辐射噪声，通过北京首都机场快轨线某高架段现场测试结果验证了预测方法的有效性。

有限元和边界元预测方法模拟振动和声能传递转换规律符合实际情况，计算精度准确可靠，但计算过程复杂，需借助多种计算软件辅助完成，同时需要对车辆、轨道，以及桥梁的几何、结构、力学等性能有较为准确的掌握，不利于推广应用。

本文针对目前城市轨道交通高架线路噪声研究预测方法中存在的不足，在偶极子预测模型的基础上区分不同噪声来源，在考虑轮轨噪声和桥梁结构噪声直接传播影响的基础上增加结构与地面之间的混响声和地面反射声的影响修正，提出了一种简化的计算模型。该模型相比之前提出的偶极子预测模型，能够区分不同噪声来源的贡献量，提高了计算精度；相较于有限元和边界元预测方法的模型，虽然计算精度降低，但易于理解和推广应用。

1 城市轨道交通高架线路噪声预测简化计算模型

1.1 模型描述

城市轨道交通高架线路噪声源包括轮轨噪声、车辆动力噪声、集电系噪声、空气动力噪声和桥梁结构振动噪声。如果列车运行速度在120 km/h以下，噪声源主要为轮轨噪声和桥梁结构振动噪声。

本文所建立的简化模型将列车视为不相干的有限长偶极子线声源，模拟轮轨噪声向空间辐射的影响。因受桥梁结构遮挡，向桥下空间辐射噪声被掩蔽，因此不予考虑。将桥梁结构振动简化为底板的振动，并忽略板沿厚度方向的应力变化，即板的内应力仅是平面坐标的函数；假设桥梁底板中心处的振动位移最大，梁端为刚性支撑边界。

1.2 轮轨直达声

将列车的每节车厢视为一个有限长线声源，声源特性具有偶极子辐射指向性。图1为轮轨直达声预测模型示意图。在受声点处的直达声声压均值为：

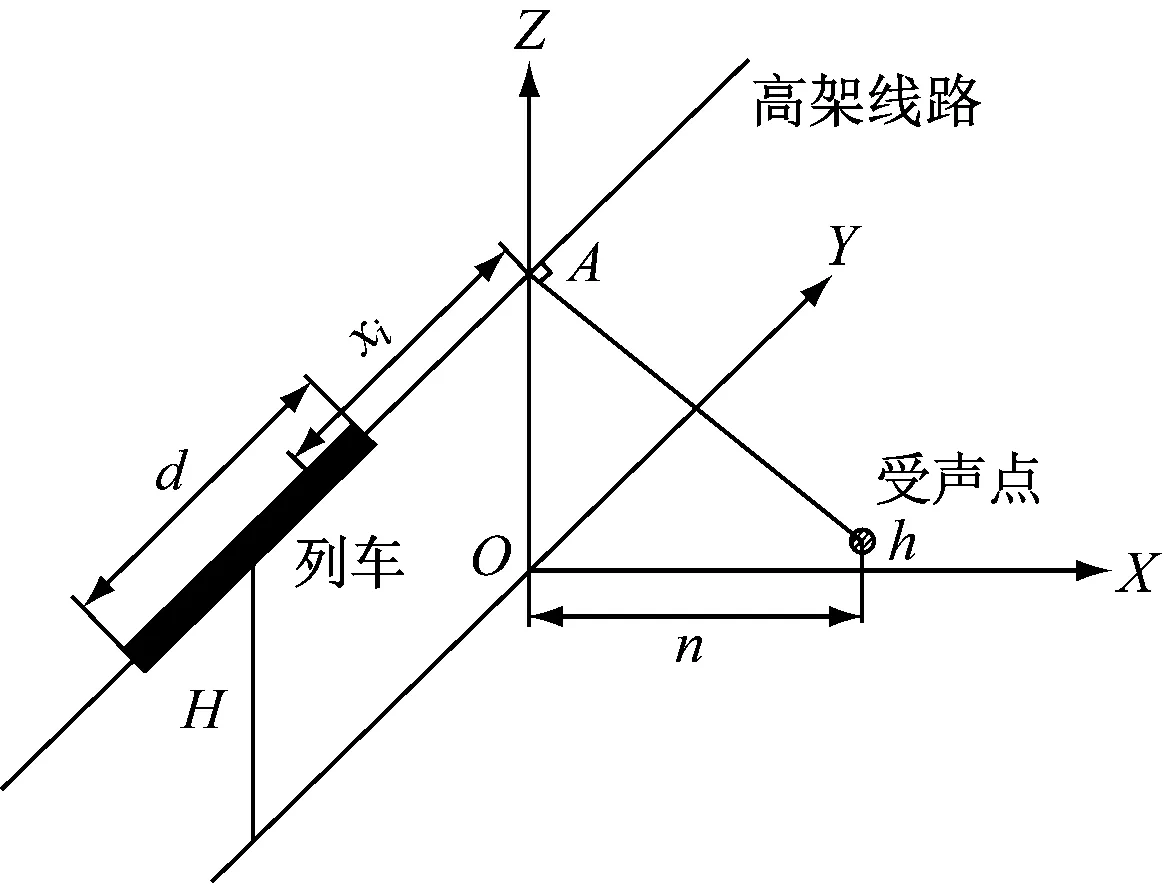
图1 轮轨直达声预测模型示意

(1)

式中：

p——直达声声压均值；

ρ——空气密度；

c——声速；

W——列车辐射声功率；

n——受声点到高架线路的最短水平距离；

l——车厢长度；

Δh——高架线路与受声点的高差；

xi——第i个车厢中点到A点的距离，A是受声点到高架线的垂直线交点；

r——声源与受声点之间距离。

当列车中点与受声点连线正好与列车垂直时，受声点处声压和声压级出现最大值，分别为：

(2)

(3)

式中：

Pmax——声压最大值；

Lmax——声压级最大值；

Pb——背景声压；

Lb——和声压级；

d——列车长度。

当已知受声点处最大声压级时，可得到列车辐射声功率：

(4)

式中：

P0——基准声压。

将式(4)带入式(1)和式(3)，并考虑列车通过时段各车厢中心到A点距离随时间的变化情况，可得到列车通过受声点的声压级与时间的关系：

式中：

Lp——列车通过受声点的声压级；

v——列车运行速度；

r0——起始时刻车头位置到A点的距离。

1.3 混响区

噪声在桥梁底板和地面之间多次反射会在梁下形成混响区。假设混响区为地面、桥梁底板及两个桥梁边界投影垂直面构成的封闭空间，图2为混响区示意图。两个投影垂直面的吸声系数均为1。混响区声压为：

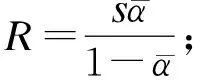
式中：

s——混响区各侧面面积之和；

a1、a2、aB、aG——分别为混响区各侧面吸声系数；

s1、s2、s3、s4——分别为混响区各侧面面积,当梁下地面为疏松地面或草地时，可通过αG进行修正。

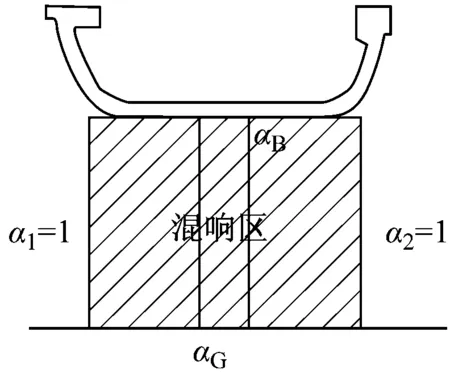
图2 桥下混响区示意图

1.4 地面反射

当梁下地面为刚性面时，应考虑地面对噪声的反射。可将刚性壁面前的声源辐射声场看作声源与一个对称位置的虚声源所产生的合声场。虚声源对受声点处的贡献与直达声强度相当，相位相反。故地面反射声也按线声源偶极子来等效计算：

式中：

Pr——虚声源在受声点处产生的声压；

ω——振动角频率；

k——波数;

r2——虚声源到受声点的距离；

H——桥梁距地面的高度。

1.5 桥梁结构振动噪声

桥梁结构振动噪声由桥梁各结构板振动产生(以底板贡献最大)，其中主要贡献为各桥板法向振动速度分量v，其三角函数表示为：

vz=v0cos(ωt-φ)

式中：

v0——振动速度；

φ——初相位。

桥板振动导致的声功率为各计算点声强的积分为：

式中：

WB——桥梁底板振动功率级；

A——桥梁底板面积。

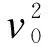
式中：

v0i——计算节点的法向振动速度，振动速度是频率的函数；

ne——计算节点数；

Ni——插值函数[8]。

受声点处的声压可认为是桥面板上各点振动导致的声压之和：

桥梁结构振动角频率ω与桥梁的结构性质有关。已有的研究表明，对于中小跨度简支梁的振动，取一阶振型就可得到满意结果[9-10]，本文研究中桥梁结构一阶振动频率为4.72 Hz。

2 高架线路噪声振动实测结果

为验证建立的简化预测模型可行性，选取实际城市轨道交通高架线路进行噪声和振动数据实测，并以测试结果进行模型验证。在上海轨道交通16号线高架段进行实际测试，该线路梁型为U型梁，梁跨为27 m，跨中横截面尺寸见图3。

测试时，列车运行速度为80 km/h，信号截取长度为6 s，测试段轨道结构为WJ-2A扣件+支撑块承轨台，测点布置形式见图3。测试时，天气为晴天，风速小于5 m/s，符合监测标准要求。列车通过时，梁跨底板测点Z振级频域如图4所，时域结果如图5所示。噪声结果见表1和图6～7。

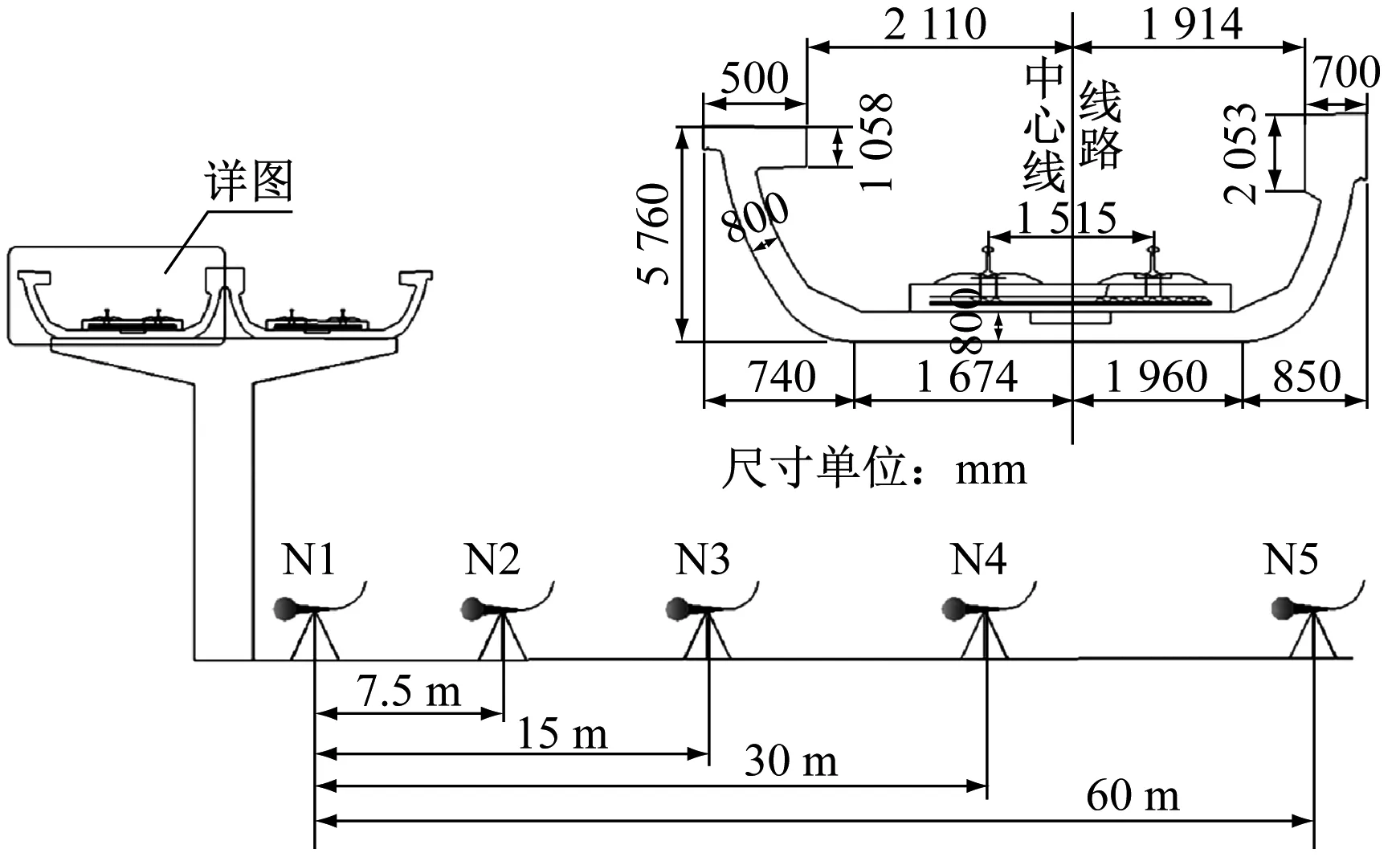
图3 测试梁跨横截面图和测试点位示意图

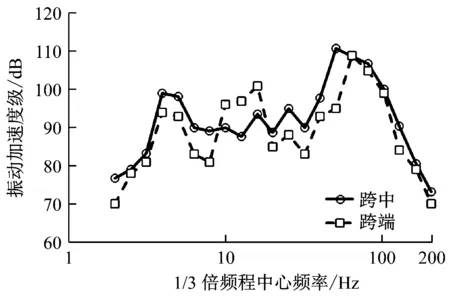
图4 桥梁底板测点Z振级1/3倍频程结果

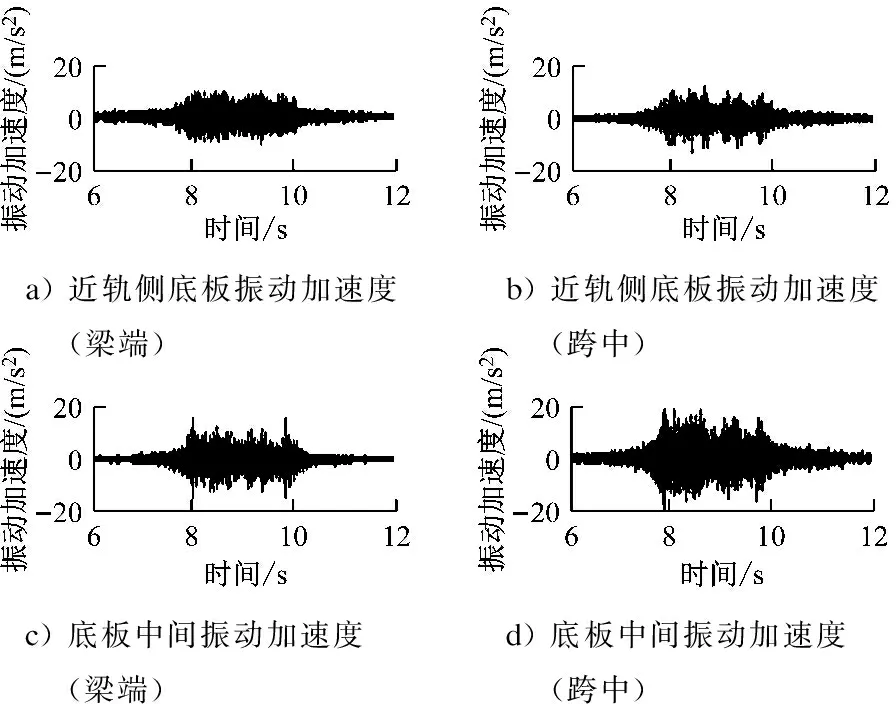
a) 近轨侧底板振动加速度(梁端) b) 近轨侧底板振动加速度(跨中) c) 底板中间振动加速度(梁端) d) 底板中间振动加速度(跨中)

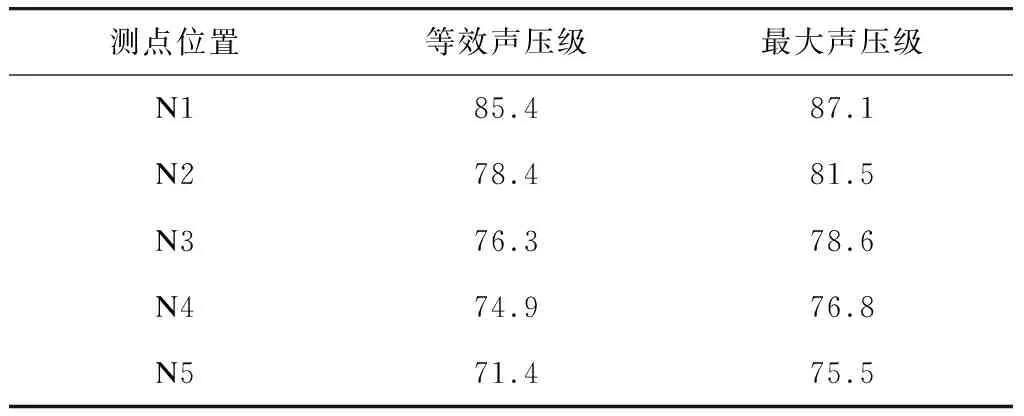
图5 桥梁底板测点Z振级时域结果

3 简化预测模型计算及对比验证

不同测点位置主要噪声贡献源不同，预测计算时不同测点位置取不同噪声贡献量叠加计算。测试选取的上海轨道交通16号线测量地段，梁下地面为疏松草地，因此预测时忽略地面反射贡献量。

图6 不同噪声测点的时域结果

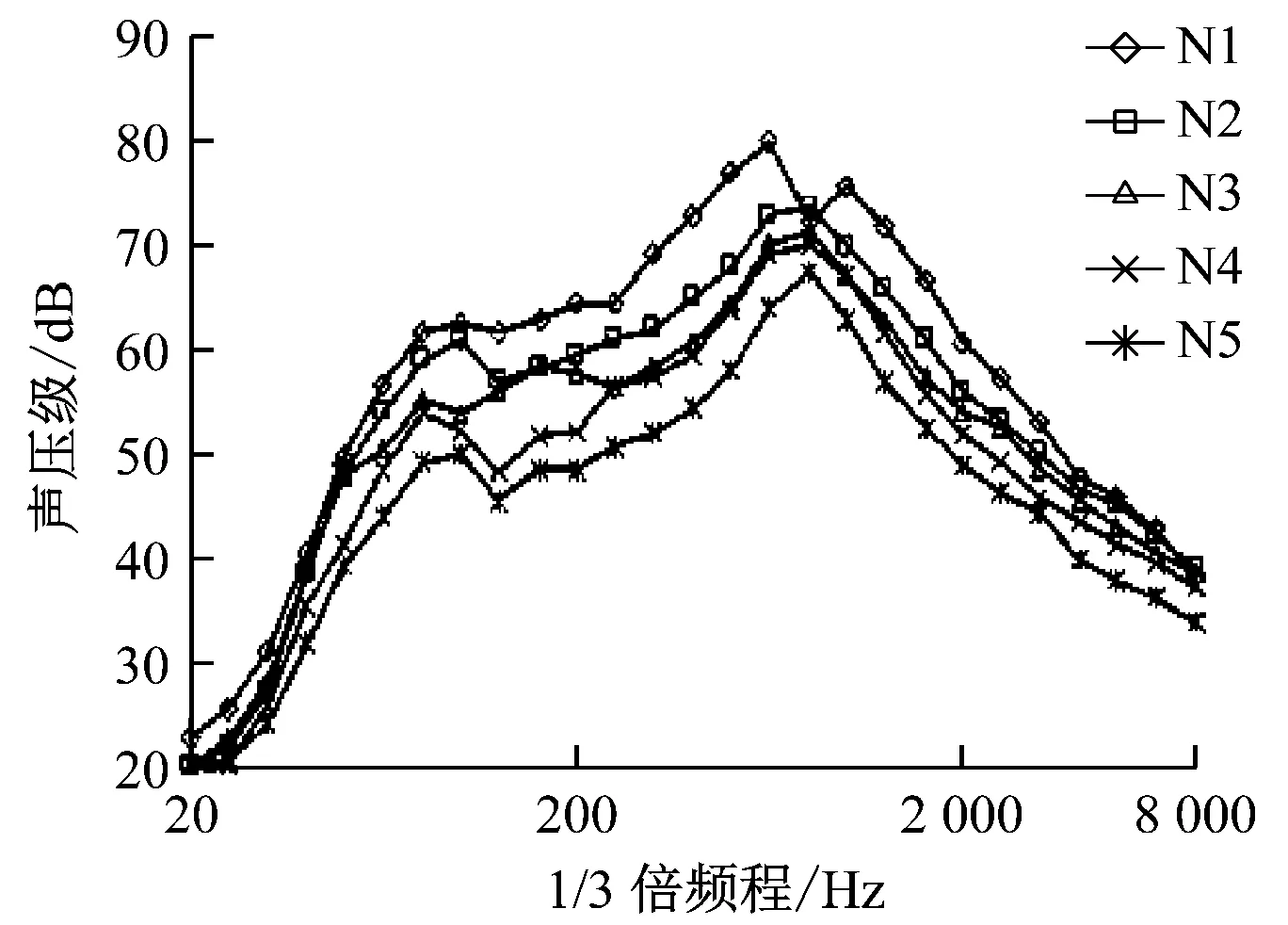
图7 不同噪声测点的1/3倍频程结果

具体计算说明：测点N1位于梁下地面以上1.5 m，桥面以上线路噪声的传播受桥面板遮挡影响，主要噪声贡献量为桥梁结构(尤其是桥梁底板)振动噪声以及桥梁结构与地面构成的混响区噪声；预测计算时以结构噪声叠加混响噪声作为预测值。测点N2—N5距离梁跨7.5～60.0 m，这些测点的噪声主要受桥梁结构噪声、混响区噪声、桥面以上线路噪声绕射影响，因此叠加上述噪声贡献量为预测值。各测点不同噪声贡献量预测计算结果见表2。预测结果与实测结果比较图如图8所示。

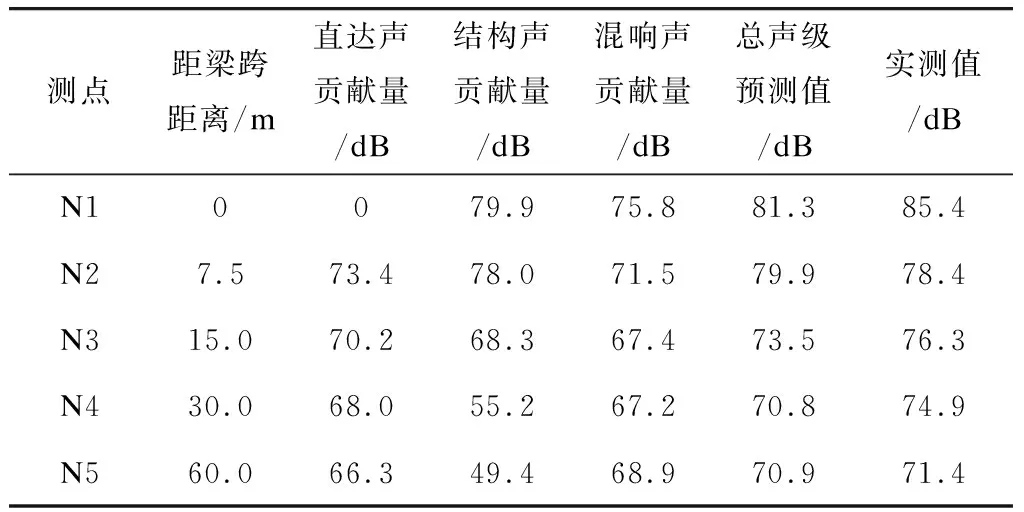
表2 不同测点噪声预测计算结果

经验算，除测点N1外，其余各测点的预测值与实测值误差在1.6～2.7 dB之间，结果表明本文所建立的简化计算模型具有较好的精度。测点N1的计算误差为4.1 dB，误差较大的原因为结构噪声计算贡献量较大。结构噪声产生的机理复杂，声压级与桥梁底板上不同位置处的振级、声振转化效率等因素有关。本文在计算中为简化计算过程，以底板中心的振动加速度结果作为整个底板的振动响应情况，未考虑底板不同位置的振动转化效率，因此导致测点N1噪声的计算结果偏高，但可作为结构噪声影响的快速、简便预测计算。

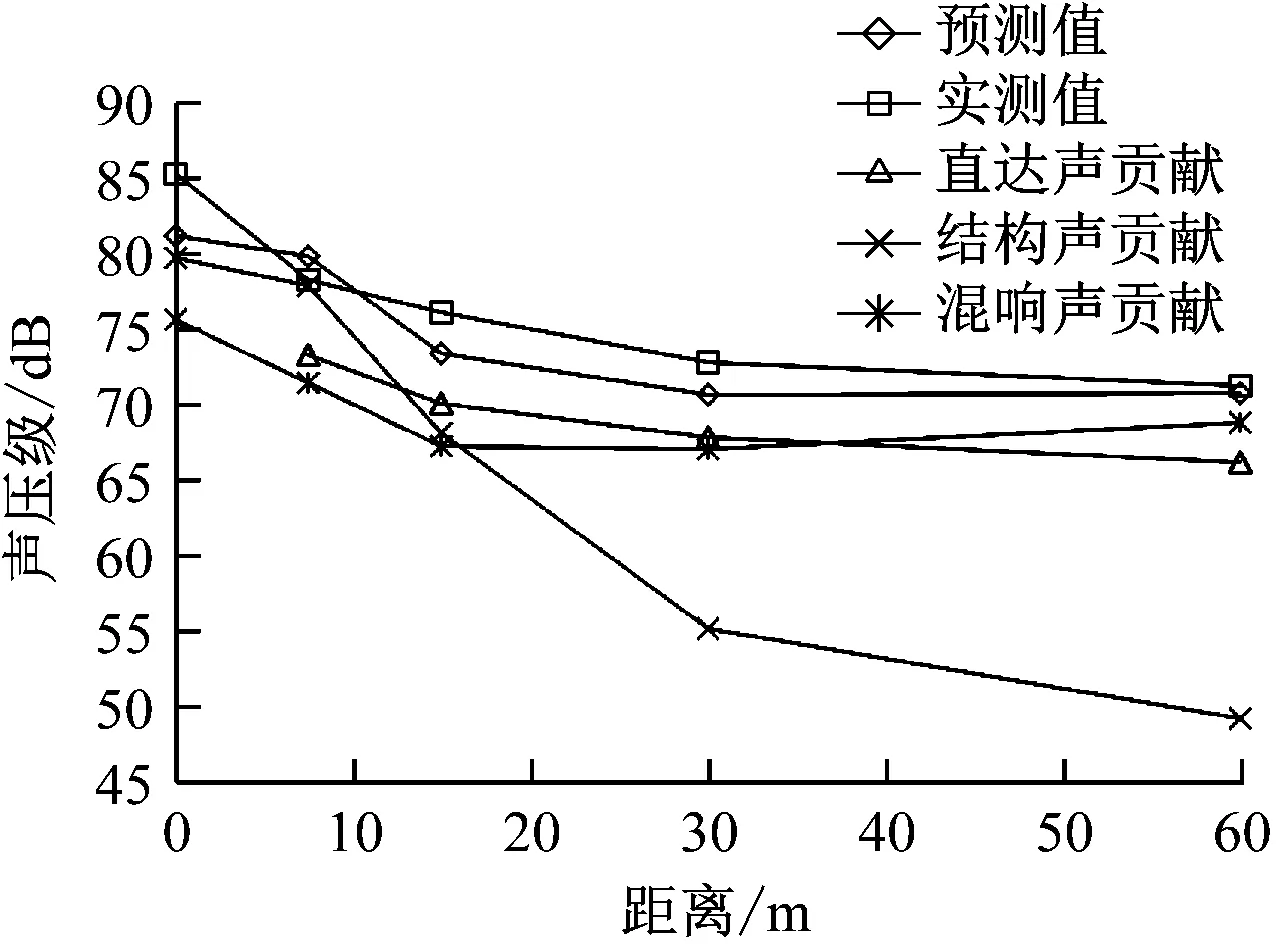
图8 预测结果与实测结果比较图

4 结语

本文所建立的预测城市轨道交通高架线路噪声源强的简化预测模型，区分轮轨噪声和桥梁结构噪声的不同贡献分别进行计算。与实测结果对比，该模型的计算精度较好，可用于高架线路环境影响预测分析。

本文所建立的计算模型为简化桥梁结构噪声复杂的传递机理，以桥梁底板中心振动结构代替梁板不同位置的实际振动情况，未考虑不同位置振动贡献程度的不同，模拟结果误差较大。下一步研究中可通过对梁板不同位置区分计算，引入不同位置处的振动转化效率修正系数，来进一步提高计算精度。