地铁车辆低落弓位受电弓线导板算法研究

2019-08-21王俊勇

城市轨道交通研究 2019年8期

贾荣陈超王俊勇

(1.北京中车赛德铁道电气科技有限公司,100176,北京;2.同济大学铁道与城市轨道交通研究院，201804，上海； 3.西南交通大学机械工程学院，610031，成都//第一作者,助理工程师)

根据地铁车辆受电弓的相关设计标准以及用户对受电弓的技术要求，设计时要求受电弓在工作高度范围内的静态接触压力保持在(120±10) N。另一方面，对受电弓的落弓高度也有要求。由于刚性接触网空间占用率低、免维护及安全可靠性高等特点，被广泛应用于地铁线路隧道区段。刚性接触网的高度通常较低，因此要求地铁车辆受电弓的落弓高度尽可能降低，以降低车辆的整体高度，减少隧道的开挖量。地铁低落弓位受电弓采用空气弹簧侧置的方式，可以将受电弓的落弓高度降至300 mm以下(基准为绝缘子安装面)。但是低落弓位受电弓驱动方式的改变却增大了其线导板的设计难度。

本文以受电弓与接触网的静态接触压力恒定为目标，提出了适用于低落弓位受电弓线导板廓形的计算算法，利用MATLAB软件编写了计算程序，并通过试验，验证了算法的正确性。

1 地铁低落弓位受电弓结构计算模型

1.1 受电弓框架结构计算模型

低落弓位受电弓是由底架、升弓装置、下臂、下导杆、上臂、上导杆、弓头等几部分组成的空间机构，并通过绝缘子与车顶固定。受电弓可以在高度方向上大范围运动以适应接触网高度的变化。在实际研究中，通常选择列车的纵剖面为研究平面，将各部分向该平面投影，简化为图1所示的计算模型。该模型为连杆机构。

图1 受电弓框架结构计算模型

图1中,A为下臂与底架间绞点，B为下导杆与底架间绞点，C为下导杆与上臂间绞点，D为下臂与上臂间绞点，E为上臂与弓头间绞点，F为上导杆与弓头间绞点，G为上导杆与下臂间绞点；Fc为弓头滑板中心，Q1、Q2、Q3、Q4、Q5分别为下臂、下导杆、上臂、上导杆及弓头组成的重心；α、β、γ、λ、δ分别为线段AD、BC、DE、GF与水平方向的夹角及CD与DE的夹角，将α设为升弓角。

1.2 几何关系

以A为原点，建立坐标系，如图1所示。根据几何关系，可得AB长度为：

AB与水平方向夹角为：

ε=arctan[(yA-yB)/(xA-xB)]

BD的长度为：

根据三角形内角与外角关系可得：

γ=∠CBD+∠BCD-∠ADB-α-δ

β=π-∠CBD-∠ABD-ε

点G的坐标为：

点E的坐标为：

EG的长度为：

在△EGF中，可以进一步求得：

λ=arctan[(yE-yG)/(xE-xG)]-∠EGF

得到点F的坐标为：

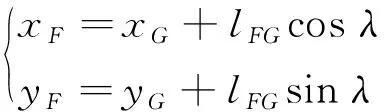
由于受电弓运动时，弓头几乎为水平状态，且滑板在列车运行方向上关于E点对称安装。因此，可以设静态接触力作用点Fc的坐标为：

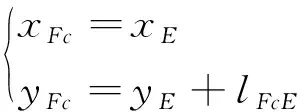
其中，lFcE表示上臂管轴中心与滑板平面的高度差，为常数。

由上述几何关系可知，受电弓框架结构的计算模型为单自由度模型，若升弓角α已知，则各点的位置即被确定。

1.3 受电弓升弓转矩函数的建立

受电弓的静态接触力由作用于下臂与底架间绞点的升弓转矩提供,各绞点润滑状态良好，因此，在计算升弓转矩时，忽略绞点的摩擦阻力。采用矩阵法对受电弓的框架结构进行受力分析，将受电弓的各部分分解出来建立计算模型，如图2所示。

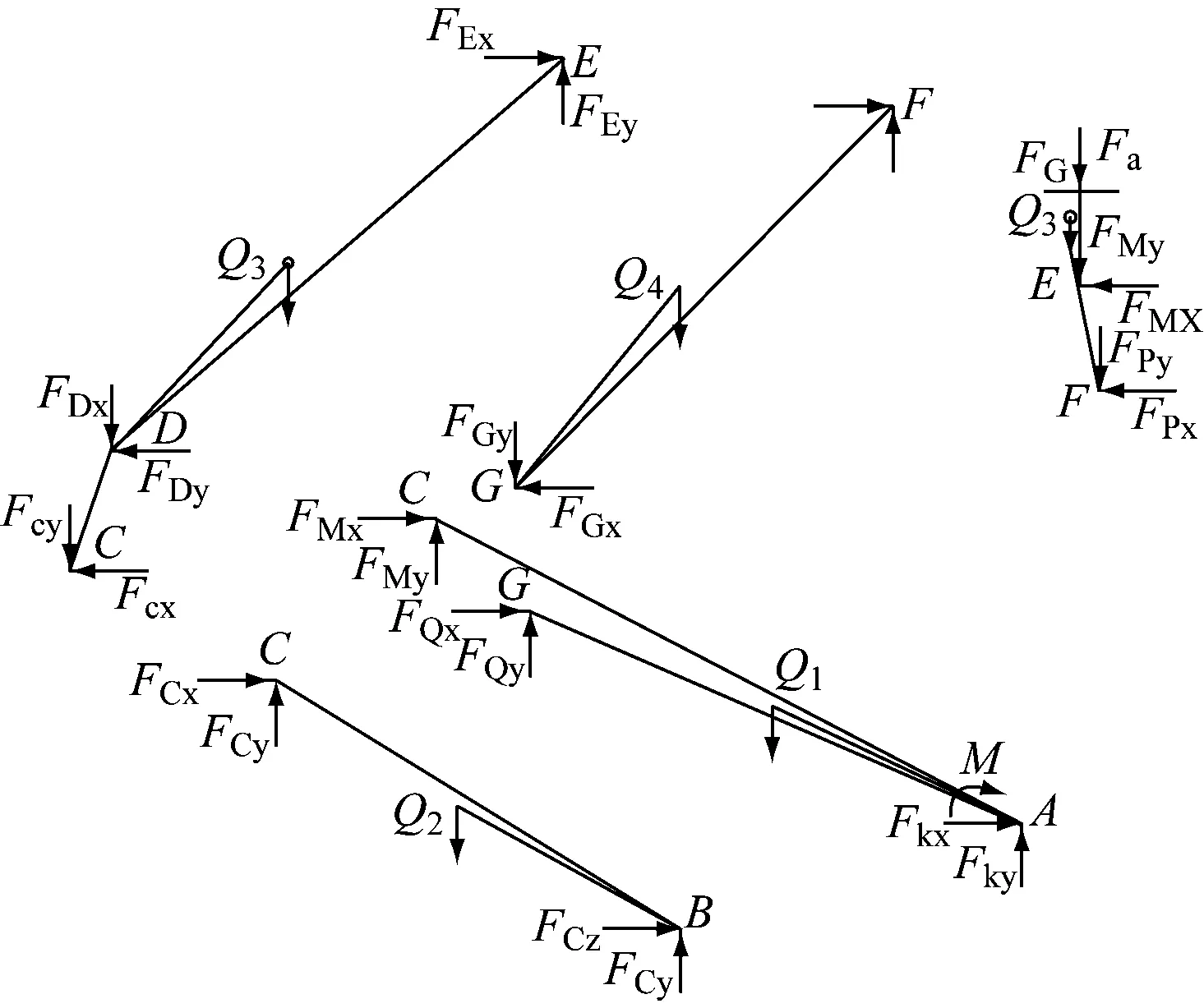
图2 受电弓各部分受力分析

根据受力分析，列出整个受电弓的平衡方程，并转化为计算矩阵;对计算矩阵进行求解，即可得到受电弓的升弓转矩M。通过对计算矩阵的分析可知，当升弓角α确定时，升弓转矩M即被唯一确定，因此可将升弓转矩设为升弓角α的函数M(α)。根据几何关系和计算矩阵利用MATLAB软件编写计算函数M(α)，以便于直接调用。根据计算结果，受电弓在工作高度范围内的升弓转矩函数图像如图3所示。

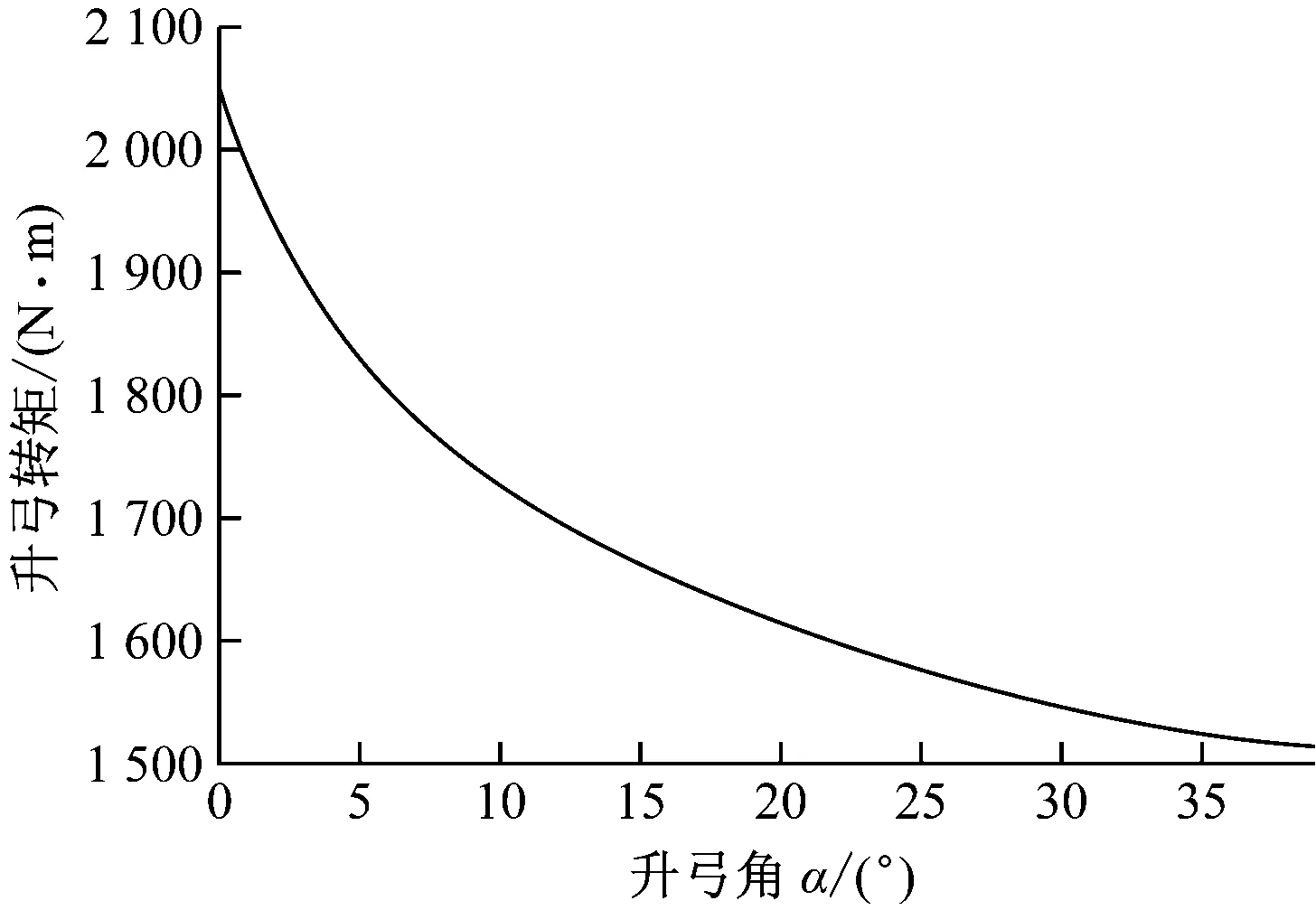
图3 升弓转矩函数图像

2 低落弓位受电弓升弓装置计算模型

地铁低落弓位受电弓的升弓装置采用空气弹簧驱动。为降低落弓高度，将空气弹簧放置在下臂侧面，如图4所示，简化为如图5所示的计算模型。

图5中，点H为升弓摆臂与底架间绞点；点K为钢丝绳安装绞点；点J为空气弹簧上端盖的中心；MN表示空气弹簧下端盖平面。

空气弹簧的输出力由输入气压和弹簧上下两端盖间的高度差共同决定，作用方向垂直于上端盖，空气弹簧的静态特征值如图6所示。空气弹簧工作时，上下端盖存在一定的夹角，但由于设计时将夹角限制在允许的范围内，因此，弹簧的输出力依然可以采用静态特征值进行计算。地铁受电弓空气弹簧的工作气压通常为0.4 MPa，两端盖间高度差h通常在100～200 mm间。在该范围内，空气弹簧的静态特征值曲线线性较好，因此进行线性差值计算，得到静态输出力f的函数h为：

f(h)=-0.062h+22.7

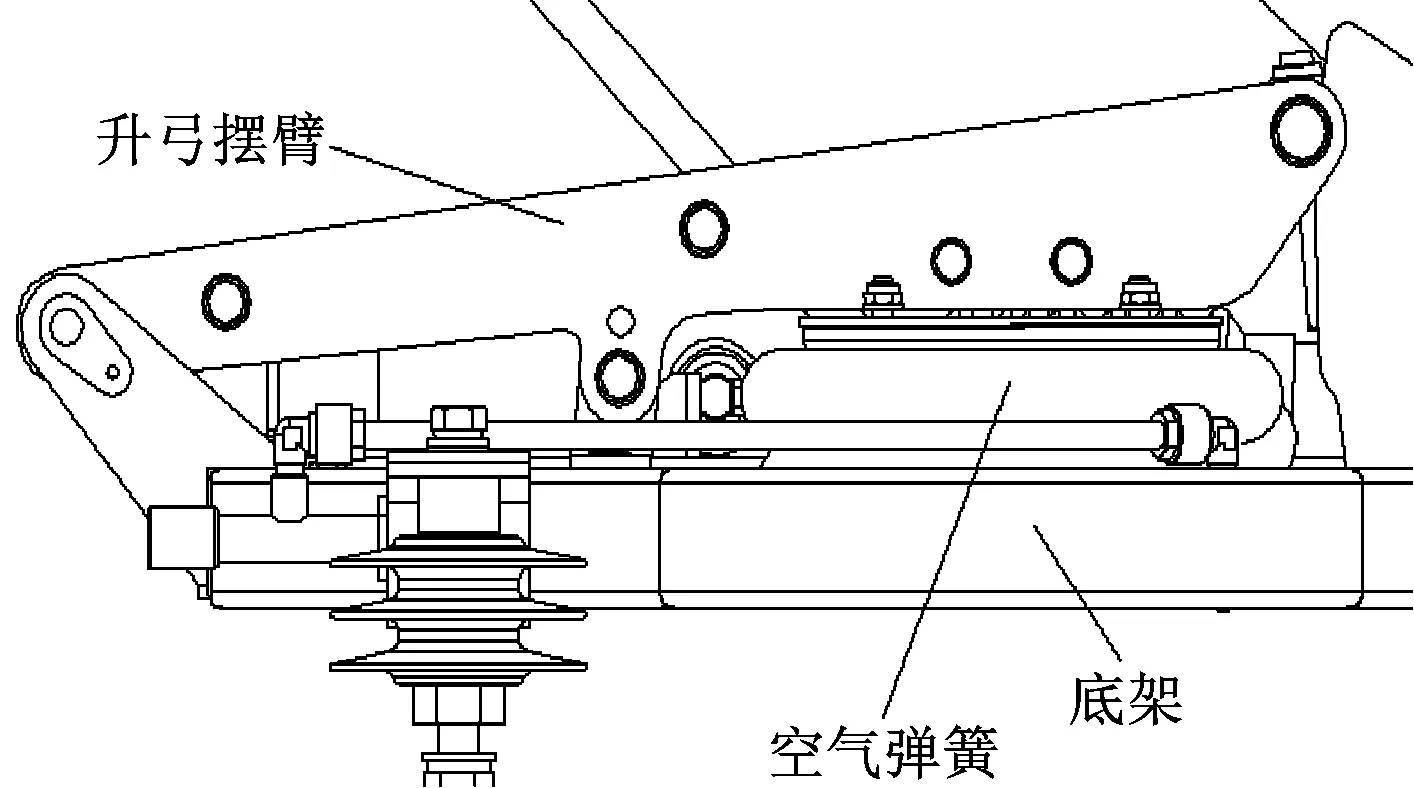
图4 低落弓位的受电弓升弓装置

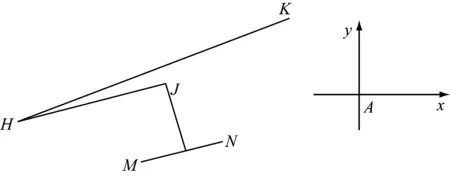
图5 升弓装置计算模型

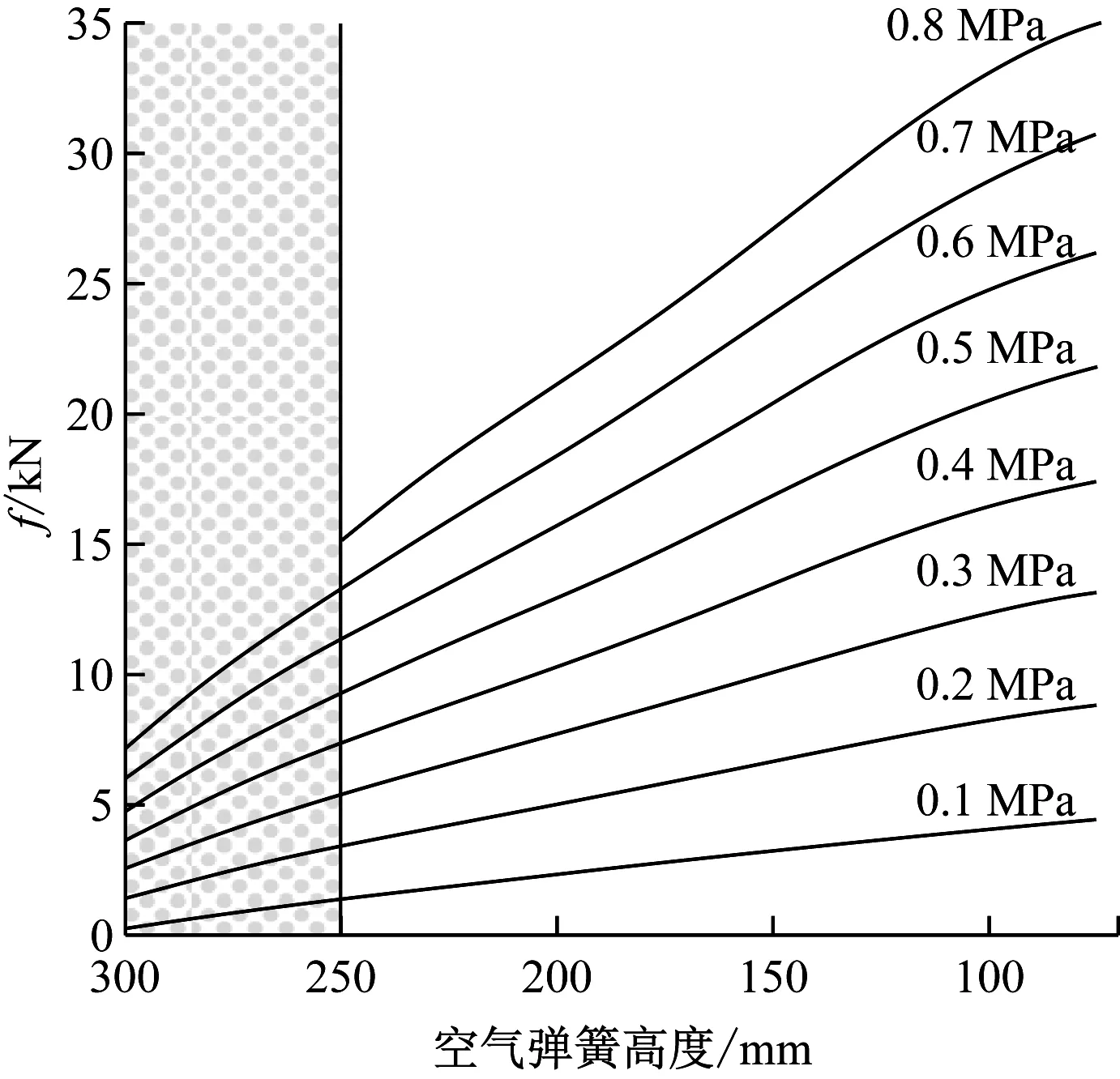
图6 空气弹簧静态特征图

3 地铁低落弓位受电弓线导板算法

3.1 受电弓工作状态计算模型

受电弓的升弓装置如图7所示。钢丝绳一端与升弓摆臂相连，另一端与安装于下臂的线导板固定，并缠绕在线导板上。通过线导板的调节作用，钢丝绳拉力产生满足升弓转矩要求的力矩。计算模型如图8所示，点P为钢丝绳与线导板轮廓线切点。

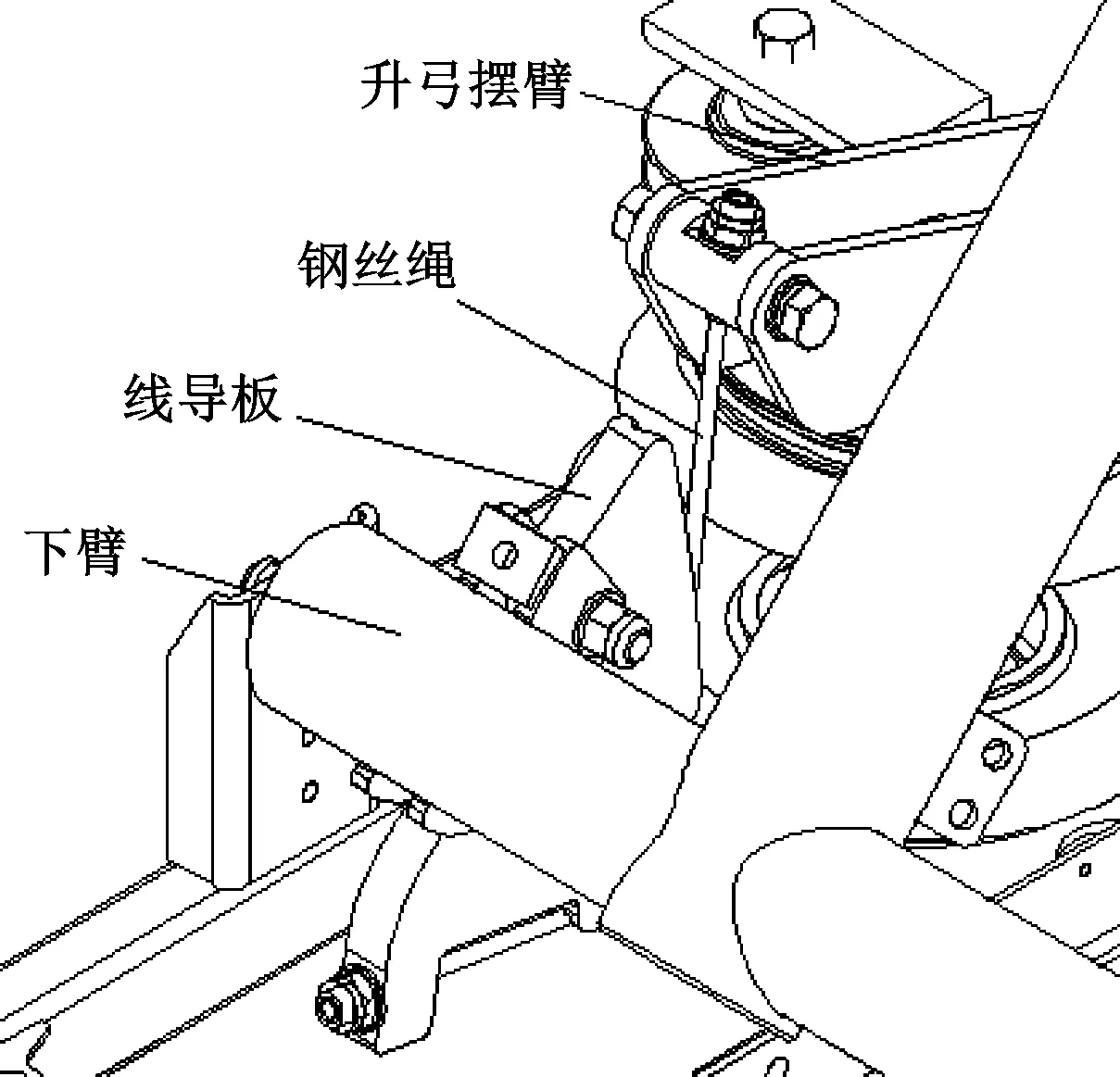
图7 升弓装置

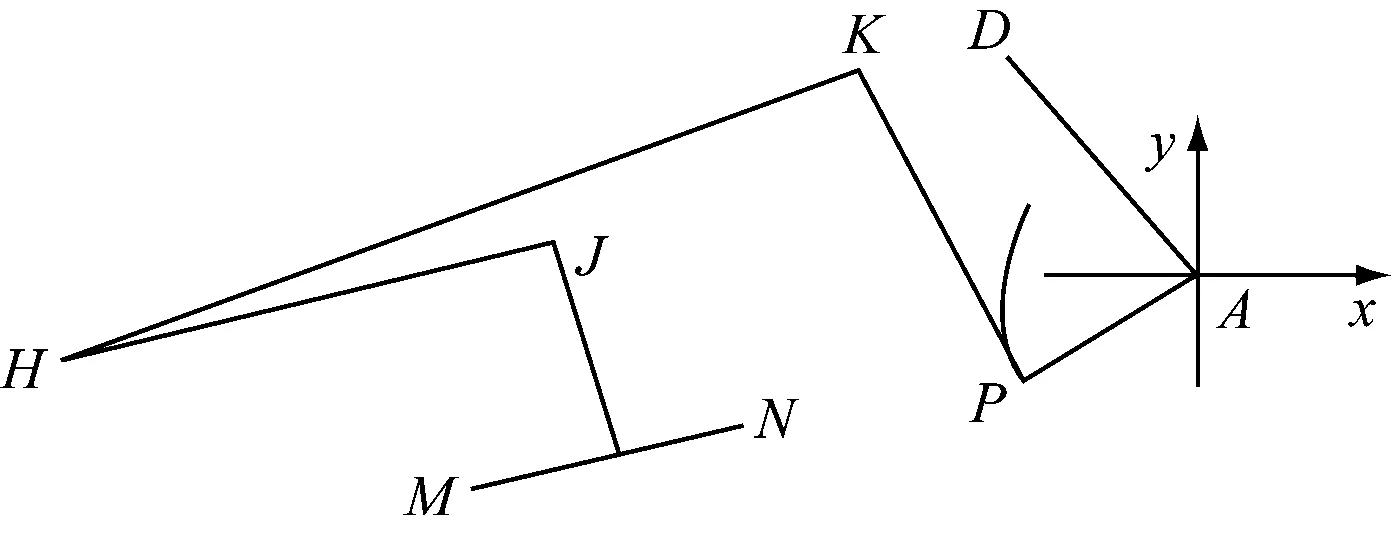
图8 受电弓工作状态计算模型

3.2 受电弓线导板算法

假设当升弓角为α时，受电弓整体处于平衡状态，静态接触压力为120 N，受电弓各部分状态如图9所示。为了模拟钢丝绳缠绕在线导板上的运动特性，线导板在计算时，将下臂杆AD逆时针旋转，对应于受电弓的降弓过程。

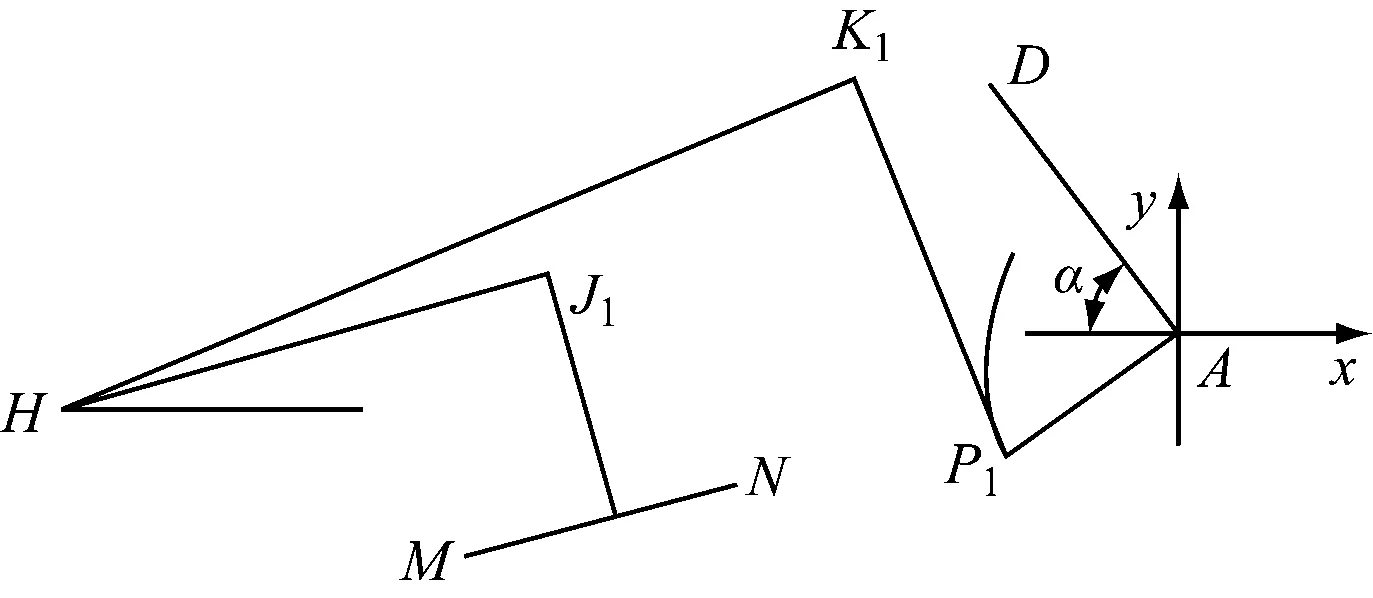
图9 受电弓平衡状态示意图

将下臂杆AD逆时针旋转Δα，升弓角变为α-Δα，升弓角为α时对应的切点P1旋转至点P2处，如图10所示。

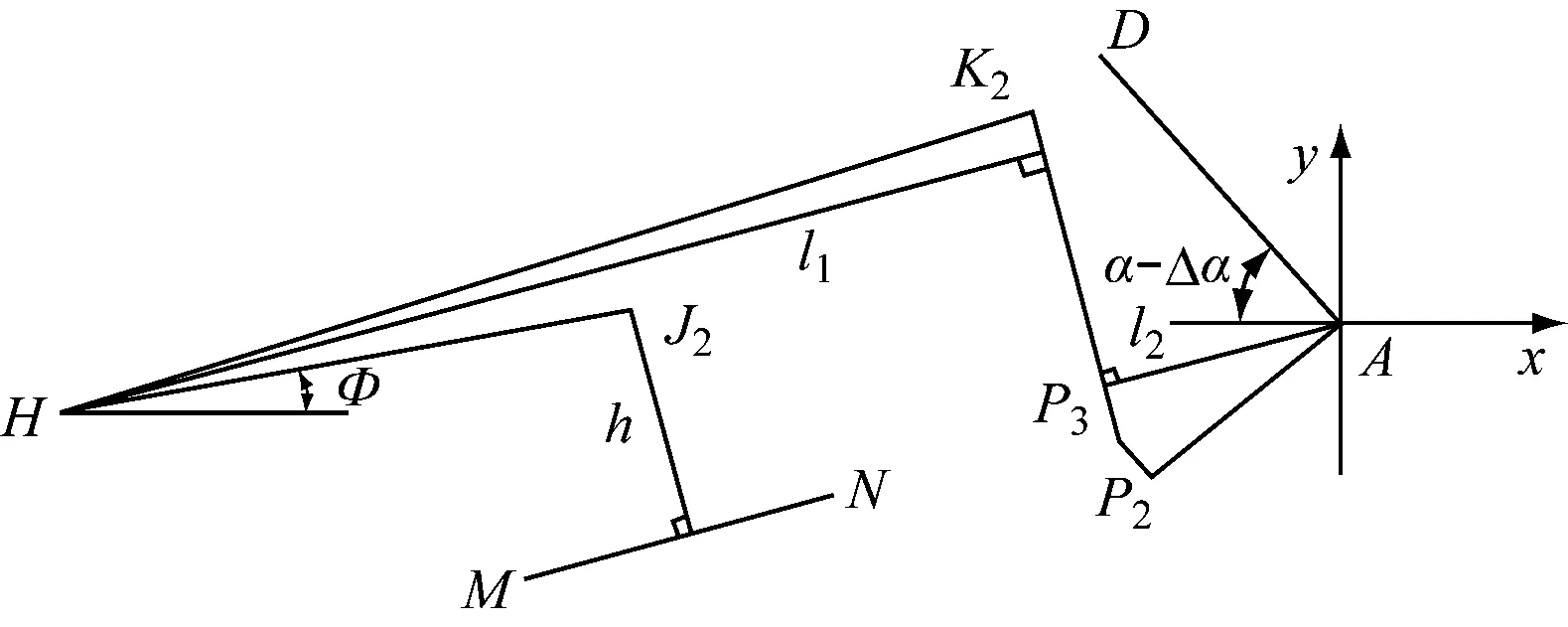
图10 旋转后受电弓平衡状态示意图

点P2的坐标为：

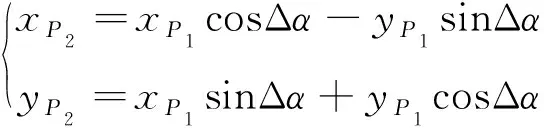
设旋转后，线导板与钢丝绳的切点为P3，图10中的点K1、点J1相应地分别运动到点K2、J2处，满足∠AP2P3=∠AP1K1，当Δα较小时，可用直线段P2P3表示线导板的轮廓曲线。根据图10中的几何关系可知，HP3的长度为：

在运动过程中钢丝绳总长不变，可得K2P3的长度为：

lK2P3=lK1P1-lP2P3

HJ2与水平方向夹角为：

φ=∠K2HP3-∠K2HJ2-arctg((yH-yP3)/

(xH-xP3))

K2的坐标为：

J2的坐标为：

由于直线K2P3不经过原点A，因此，设K2P3的表达式为：

ax+by+1=0

求解如下方程：

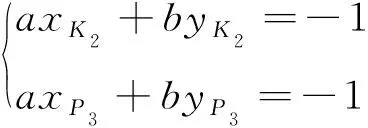
可得a和b的值。则点H到直线K2P3的距离l1为：

点A到直线K2P3的距离l2为：

同理，求得J2到MN的距离h。

通过计算可知，当切点P3坐标确定后，受电弓升弓装置的状态即被确定。假设此时受电弓处于静态接触力为120 N的平衡状态，平衡方程为：

式中：

T——钢丝绳拉力；

f(h)——空气弹簧推力；

M(α-Δα)——升弓转矩。

将T消掉，可得：

M(α-Δα)=f(h)lHJ2l2/l1

因此，只需确定点P3的坐标。利用MATLAB的模式搜索算法，将对点P3的坐标求解过程转化为优化问题，优化的初始点为点P2。将几何关系和平衡方程转化为约束条件，优化方向为lp2p3最小，即可求得点P3的坐标。在受电弓的工作高度范围内，对上述过程进行多次循环，当计算间隔足够小时，可得线导板轮廓线上的点集，进行光顺化，即可得到符合要求的线导板轮廓曲线。