径向型高温超导轴承悬浮特性的有限元分析

2019-08-21周艳秋余志强

城市轨道交通研究 2019年8期

周艳秋余志强

(1.大连科技学院电气工程学院,116052,大连；2.石家庄铁道大学电气与电子工程学院，050043，石家庄//第一作者，副教授)

近年来，随着新型超导材料的成功研制，高温超导技术得到了快速发展。其中，高温超导磁悬浮具有无源自稳定的优良悬浮特性，其相关应用已经成为国内外研究的热点之一[1-3]。高温超导轴承是其中的重要代表(以下简称“超导轴承”)之一[4]，由超导定子和永磁转子两部分组成，如图1所示。在设计和优化超导轴承结构时，采用数字方法分析其悬浮特性是非常必要的。

本文采用H法(磁场强度法)在二维轴对称空间建立了径向型超导轴承的有限元数学模型。超导体E-J关系(电场强度与电流密度的关系)采用幂指数模型。通过试验测量值与数值计算结果的比较，验证了本模型的正确性。在此基础上，应用本模型分析了径向型超导轴承的电磁特性。本文提出的数学模型不仅能够分析大功率负载的径向型超导轴承的电磁特性，而且对于内转子和外转子两种类型的超导轴承均适用。

1 二维轴对称空间H法有限元模型

1.1 模型建立

本文试验用的径向型超导轴承装置2D(二维)轴对称模型原理图如图1左图所示。原理图中参数含义及其数值见表1。

如图1 a)所示，径向型超导轴承装置的超导定子由16个超导块材组成的2层超导环组成，永磁转子由3个永磁环和4个聚磁铁环组成。所建立的2D轴对称模型结构和尺寸与试验装置完全相同。

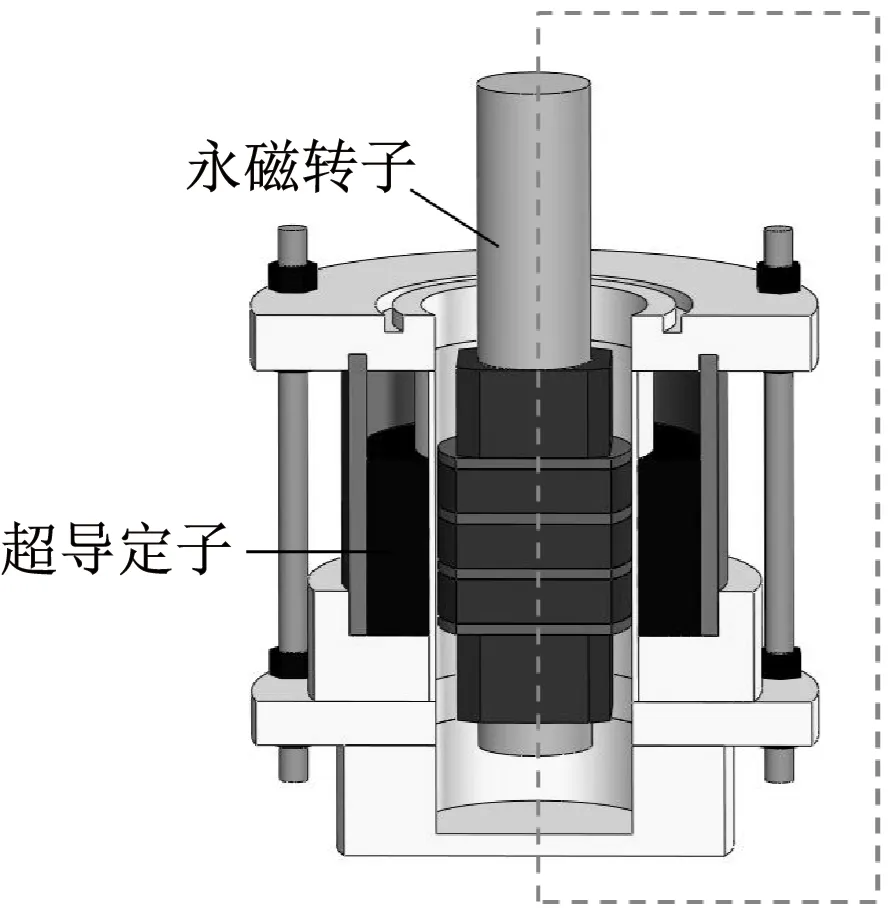
a) 结构图

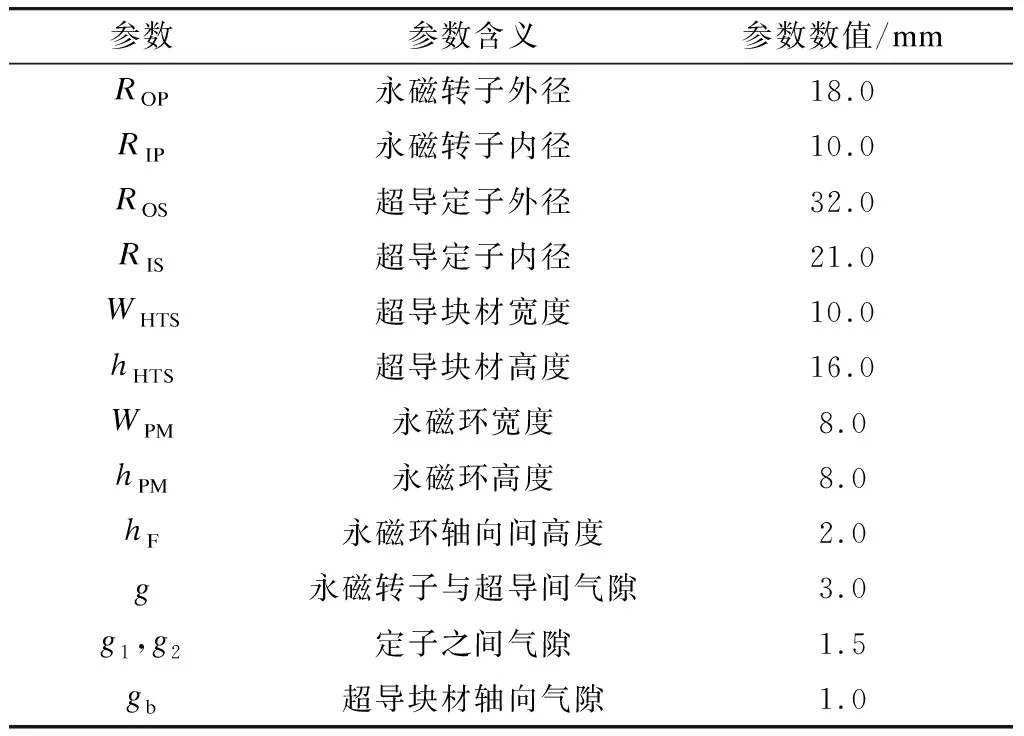
参数参数含义参数数值/mmROP永磁转子外径18.0RIP永磁转子内径10.0ROS超导定子外径32.0RIS超导定子内径21.0WHTS超导块材宽度10.0hHTS超导块材高度16.0WPM永磁环宽度8.0hPM永磁环高度8.0hF永磁环轴向间高度2.0g永磁转子与超导间气隙3.0g1,g2定子之间气隙1.5gb 超导块材轴向气隙1.0

如图1 b)所示，在二维轴对称空间里，向量H具有两个自由度：Hr和Hz。电流密度J和电场强度E仅在φ方向具有非零分量：Jφ和Eφ。根据Ampère定律，电流密度J可表示为：

(1)

式中：

z——二维坐标纵轴坐标值；

r——二维坐标横轴坐标值；

超导体E-J关系采用幂指数模型形式：

(2)

式中：

Esc——超导块电场；

E0——常量，取值为1×10-4V/m；

Jc——临界电流密度；

Jsc——感应电流密度；

ni——定义为U0/kT，其中U0和k分别为超导体的钉扎势能和Boltzmann常量。

采用Kim模型[5]描述外场强度对临界电流的影响。引入超导体的等效电阻率(effective resistivity)ρsc计算超导体的内部磁场，即其定义为：

(3)

将本构关系E=ρJ和Ampère定律(1)式代入到法拉第电磁感应定律▽×E=-μ∂H/∂t中，得到关于向量H的抛物型偏微分方程：

(4)

式中：

μ——磁导率;

ρ——电阻率;

▽——梯度算子;

t——时间。

(4)式即为本模型的电磁场控制方程。该方程较为简洁，体现了H法的优越性。

1.2 数值计算

本节采用伽辽金法和格林公式对上面得到的电磁场控制方程(4)式进行推导，得到其弱形式为：

(5)

式中：

S——整个求解域；

Г——S的边界；

∂H/∂n——边界上法向微分，n为S表面法向单位矢量；

W——向量H的权函数。

对计算域进行网格划分，选择一阶三角形单元为试探函数，则在一个网格单元里，向量H的表达式为H=Hj，e(t)Nj，j=1，2，3,e表示单元；根据伽辽金法，权函数与试探函数相同即W=Ni，i=1，2，3；式中i，j是单元节点的编号。这样，在网格单元的一个节点上的弱形式方程可以写为：

(6)

在时域中，采用后向Euler法对时间导数进行离散化处理，将每个单元质量矩阵和单元刚度矩阵进行扩充，并把扩充后的矩阵中具有相同下标的元素进行累加，将单元列向量扩充为含所有节点向量的列向量。这样，就得到了该非线性系统的最终的有限元方程，其形式如下：

([M(μ)]+[S(ρ)]·Δt){Hc}=

[M(μ))]{Hc-1}

(7)

式中：

Δt——连续时间步的时间间隔；

c、c-1——分别代表当前时间步和上一个时间步。

对应于单元矩阵，[M(μ)]和[S(ρ)]分别为非线性系统的质量矩阵和刚度矩阵。列向量{Hc-1}在本时间步为已知，放在方程的右侧。

径向型超导轴承的悬浮力F，是永磁转子的磁场作用到超导定子中超导块材的感应电流所产生的电磁力在轴向的分量。因为超导块材中的感应电流密度Jsc为φ方向，所以产生悬浮力的外磁场方向为径向，即磁场的径向分量Br。根据Lorentz方程和有限元法的特性，悬浮力F的公式可表示为：

(8)

式中：

Br——磁场的径向分量;

ΔSsc,e——超导域网格单元的面积均值；

Ng——网格单元的数量；

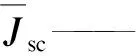
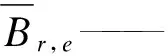
数值计算的计算流程如图2所示。

2 结果与讨论

本节应用所提出的数值计算方法，计算径向型超导轴承模型的悬浮力并与测量结果进行比较，然后分析其电磁行为。在计算的过程中，超导定子保持静止，冷却温度为77.3 K。永磁转子的移动速度为1 mm/s，移动范围为0～10 mm。在超导体的幂指数模型中，ni通过U0/kT计算，其值为15。

图3所示为径向型超导轴承悬浮力的计算结果，从图中可以看出随着永磁转子的轴向移动，悬浮力呈现出非线性变化。悬浮力上升段曲线可以分成两部分：线性上升段(对应的移动距离为0～5 mm)和饱和段(对应的移动距离为5～10 mm)。在线性上升段，悬浮力几乎线性上升，临界电流密度Jc高的曲线更接近测量曲线。在饱和段，悬浮力曲线的增加率逐渐变慢，在悬浮力达到最大值后变成负值。悬浮力的这些非线性特征主要是由于场冷条件下的磁通钉扎效应造成的。也就是在线性上升段，超导块材的捕获磁通的数量几乎保持不变，感应电流较大，外磁场较强，所以悬浮力随着永磁转子的移动迅速增加。而在饱和段，随着永磁转子的继续移动，超导块材受到的外磁场变弱，导致了悬浮力增加缓慢进而减少。就悬浮力曲线的形状而言，计算曲线反映了以上两部分的特性。

图2 计算流程图

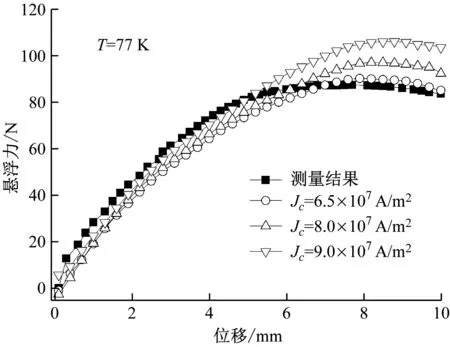
图3 悬浮力数值计算结果

2.1 悬浮力的计算

图3亦清楚地表明了计算曲线的变化趋势与测量曲线是一致的。随着Jc的增加，计算曲线的最高点亦上升。由于试验中的超导块材为单晶熔融织构的YBCO材料，所以计算中Jc分别设置为6.5×107A/m2、8.0×107A/m2以及9.0×107A/m2，这些值均在材料可达到的正常范围内。当Jc=6.5×107A/m2时，计算曲线在线性上升部分的最大误差为9.2%，饱和部分的最大误差仅为3.7%，与测量结果具有较好的一致性。

2.2 电磁行为分析

图4为永磁转子沿轴向移动的6个位移处的计算域中磁场的分布情形。由图4可以看出，大量的磁力线集中分布在聚磁铁环附近，一小部分磁通线渗入到超导块材的边缘然后穿出超导块材返回到相邻的磁极附近。由于超导体的强抗磁性，只有非常少的磁通线进入到超导块材的内部。因此，大部分磁力线被限制在了2个小的气隙中：永磁转子和超导定子之间的气隙(图1b中标记为g)和2个超导环(图1b中标记为超导块材)之间的轴向气隙(图1b中标记为gb)。从图5可以看出，超导块材中感应电流主要分布在其边缘部分，因此在超导块材的内边缘部分存在较大的电磁力。

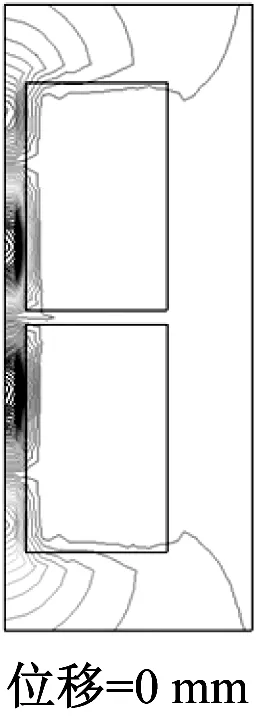
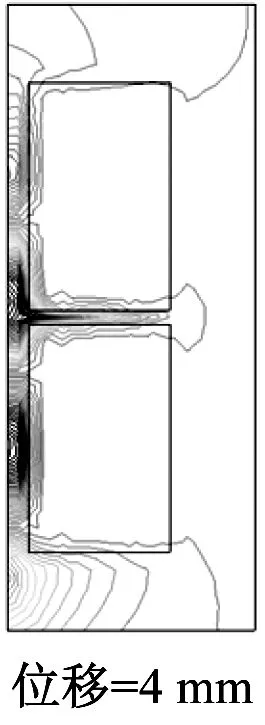
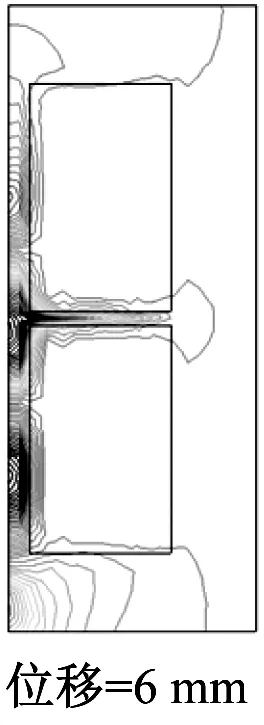
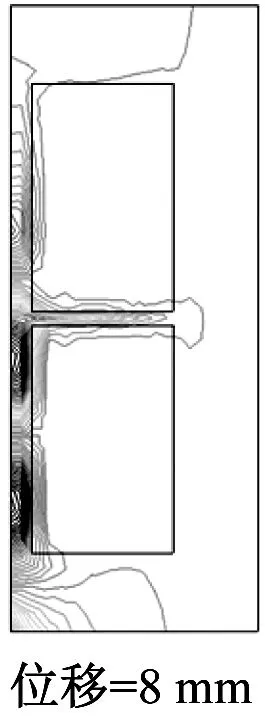
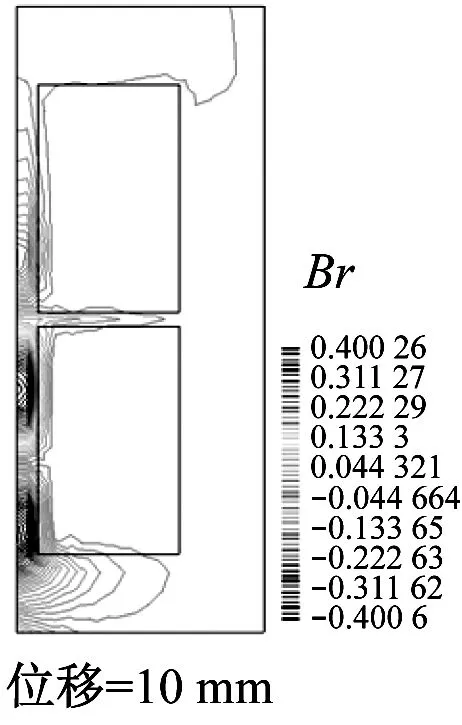
图4 不同位置时计算域的磁场分量Br分布

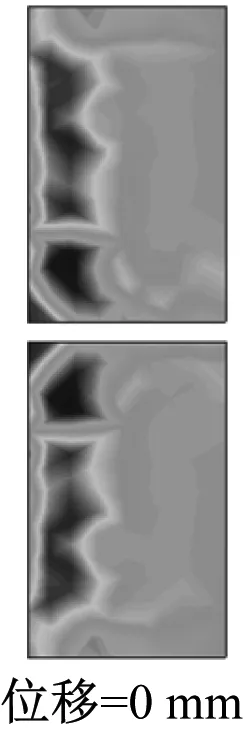
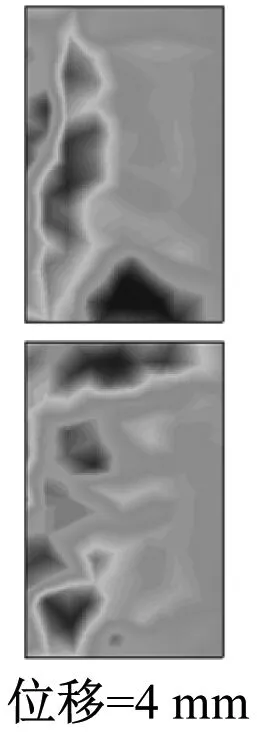
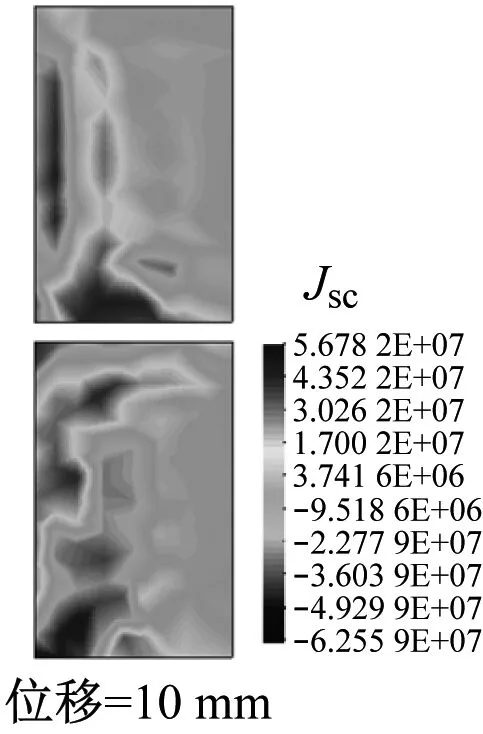
图5 不同位置时超导块材中感应电流密度Jsc的分布

为了定量说明超导块材中的磁场和电流密度的变化情况，在图1b)下方超导块材的横截面上选取了A—G 7个点，其位置如图6示。

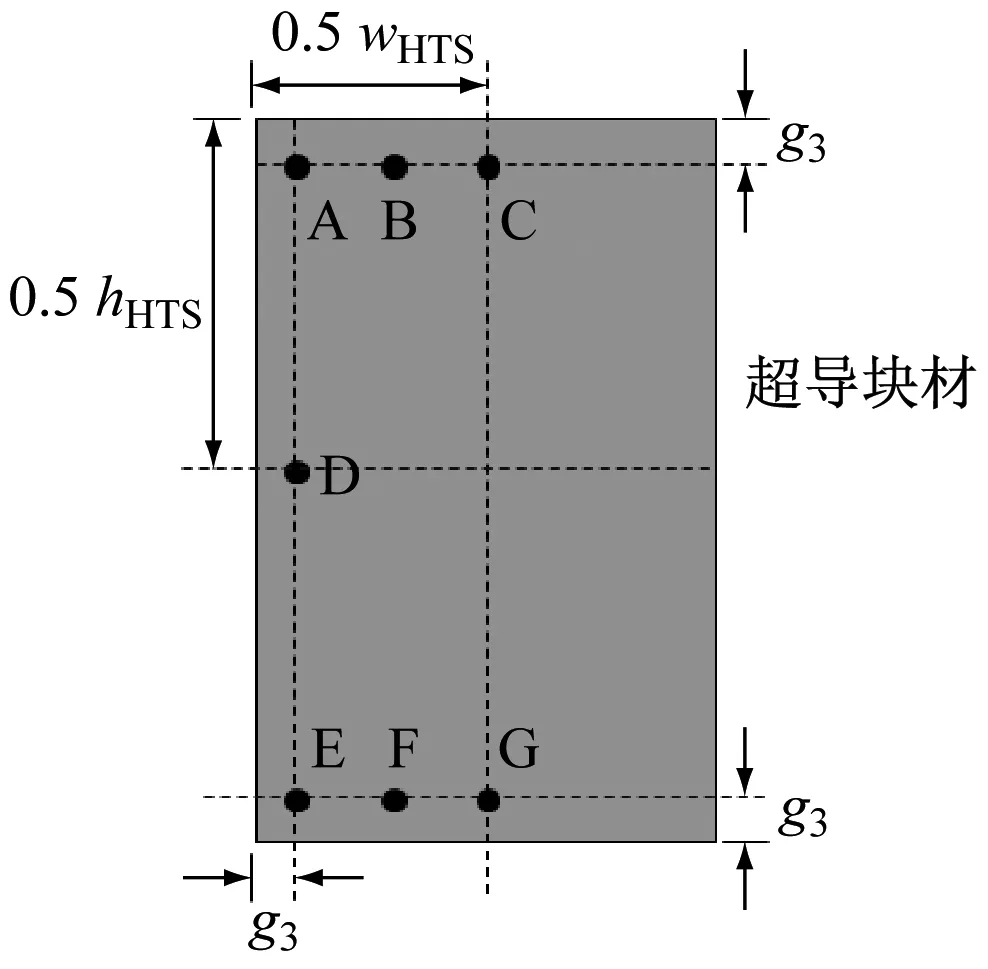
注:g3——A—G点各点到超导块材边缘的距离

下文定量地说明这7个点的磁场和感应电流密度。图7～11分别为磁场和感应电流密度随永磁转子轴向移动时的数值变化图。

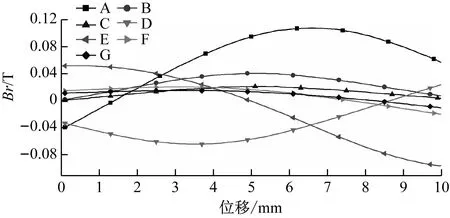
图7 永磁转子轴向移动时A—G点磁场径向分量Br

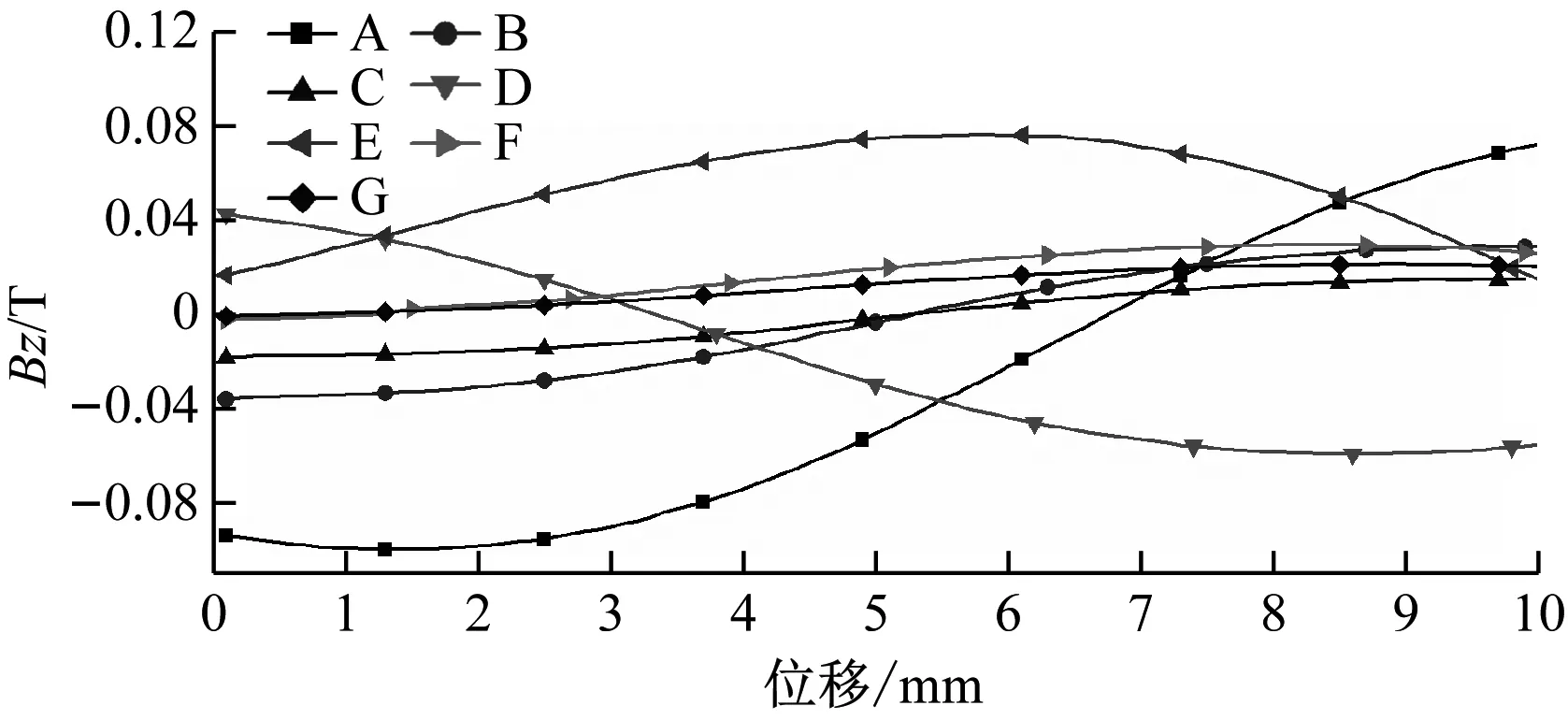
图8 永磁转子轴向移动时A—G点的磁场纵向分量Bz

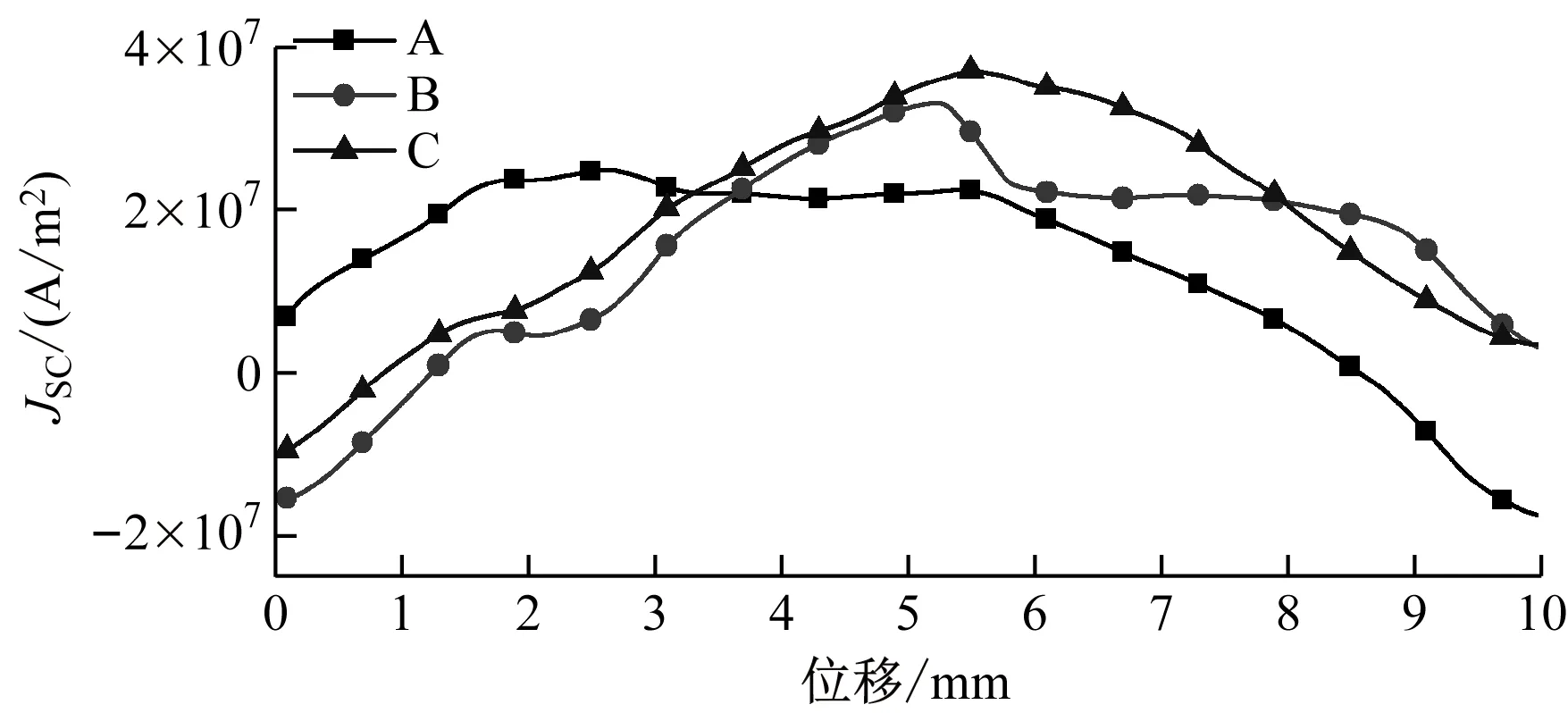
图9 永磁转子轴向移动时A、B、C点感应电流密度

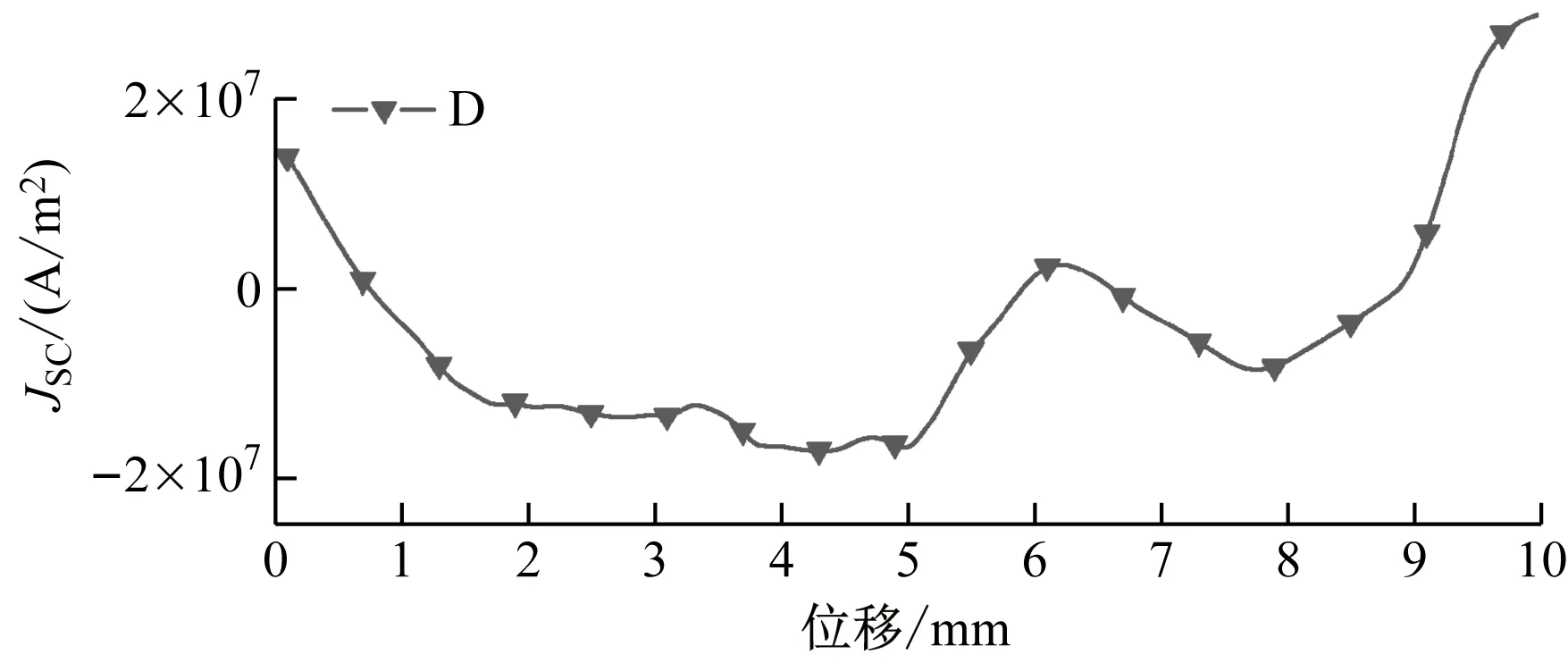
图10 永磁转子轴向移动时D点感应电流密度

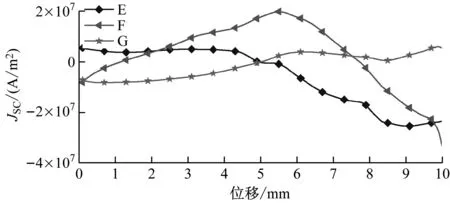
图11 永磁转子轴向移动时E、F、G点感应电流密度

设置每个点到离它最近的超导块材边线的距离为1 mm。对于A、D、E点，它们磁场的幅值相对较高，如图7～8所示。这是因为这些点距离永磁转子最近，渗入进来的磁通线较多的缘故。尽管A点和E点距离超导块材的两条边都是最近的，但是A点同时离气隙gb很近，其磁场幅值是最大的。从数值上看，A点Br和Bz的幅值分别为0.107 6T和0.099 8T。图7亦清楚的表明，对于B、C、E、F点，其磁场幅值随永磁转子的移动而减少。另一方面，由于磁通钉扎效应和磁场的连续性，在永磁转子移动的过程中，每个点处磁场的变化曲线为光滑的波浪线，变化较为缓慢。

从图9～11可看出：G点的感应电流密度的变化量是最小的，其范围为-8.118 6×106～7.245 4×106A/m2，这是因为有较少的磁通线渗入到G点，磁场变化较小。注意到由于较多的磁通线渗入到A点和E点，使得它们的磁场幅值较大，但它们的感应电流密度并不是较大的。也就是说，较高幅值的磁场并不能产生较大的感应电流，即感应电流随磁场变化的增大而增加。最大的电流密度出现在C点，其值为3.789×107A/m2。图5中C点处的较深颜色也能定性地反映这个结论。

通过以上分析表明，本文提出的有限元数学模型能够用于分析包含多层超导环和多层永磁环的径向型超导轴承的电磁行为，计算其悬浮力。