城市轨道交通列车运行节能策略研究

张赟昀

(深圳地铁建设集团有限公司, 518035， 深圳//工程师)

据统计，城市轨道交通列车的牵引能耗在列车总能耗中的占比达到60%[1]。因此牵引能耗是城市轨道交通列车运行节能的主要突破点。

目前，国内外对列车运行能耗的研究对象主要是单列车节能与多列车节能[2]。其中，多列车节能方式主要是多车追踪节能以及考虑时刻表的再生制动节能[3]。列车运行节能的限制条件也由原先的强约束条件逐步转向更接近现实运行情况的弱约束条件；列车运行节能优化目标也逐步由原先的仅考虑能耗指标转向综合考虑列车运行时间、运行能耗、停车精准度、乘客舒适度等多个指标[4]。研究列车运行节能的算法主要有数值法、解析法和智能算法[5-7]，三种算法各有其优缺点。考虑到解析法理论比较复杂，数值法存在求解缓慢问题，而智能算法适应性强、可移植性高，因此本文采用智能算法。

1 列车运行数学模型

1.1 列车运动学模型

参照《列车牵引计算规程》建立式(1)所示的列车运行单质点模型。

(1)

式中：

Fp——单位质量列车受到的牵引力；

fb——单位质量列车受到的制动力；

f0(v)——单位质量列车受到的基本阻力；

fadd(x)——单位质量列车受到的线路附加阻力；

x——列车在线路中的位置；

t——运行时间；

p——列车采用的牵引系数；

z——列车采用的制动系数；

v——列车运行速度。

1.2 适应度衡量指标模型

式(2)为运行过程中的能耗、乘客舒适度以及运行时间这3个指标的舒适度隶属度函数。

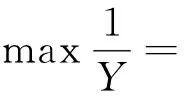
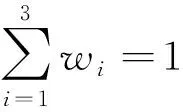
(2)

式中：

Ke——列车能耗；

Kt——列车运行时间；

Kc——乘客舒适度；

F(x)——Ke、Kt、Kc的综合衡量函数；

Wi—w1∈[0.5,0.7];w2∈[0.2,0.3];w3∈[0.2,0.3]

Et——列车牵引能耗；

Er——列车巡航能耗；

Eb——列车制动能耗；

E0——列车惰行能耗，取值为0；

T——列车运行时间；

Ta——时刻表规定运行时间；

ta——可接受的时间误差；

a——目标舒适度值；

σ——模型宽度。

1.3 基于多种群遗传算法的列车节能策略

基于多种群遗传算法的列车节能策略：基于线路数据及相关的列车运行数据进行相应的受力分析，然后利用ATO(列车自动运行)的高层结构并采用多种群遗传算法对列车推荐速度曲线进行优化；利用ATO的底层结构并采用PID(比例积分微分)跟踪策略跟踪优化后的速度曲线，得到列车实际运行的能耗。图1为ATO系统结构图。

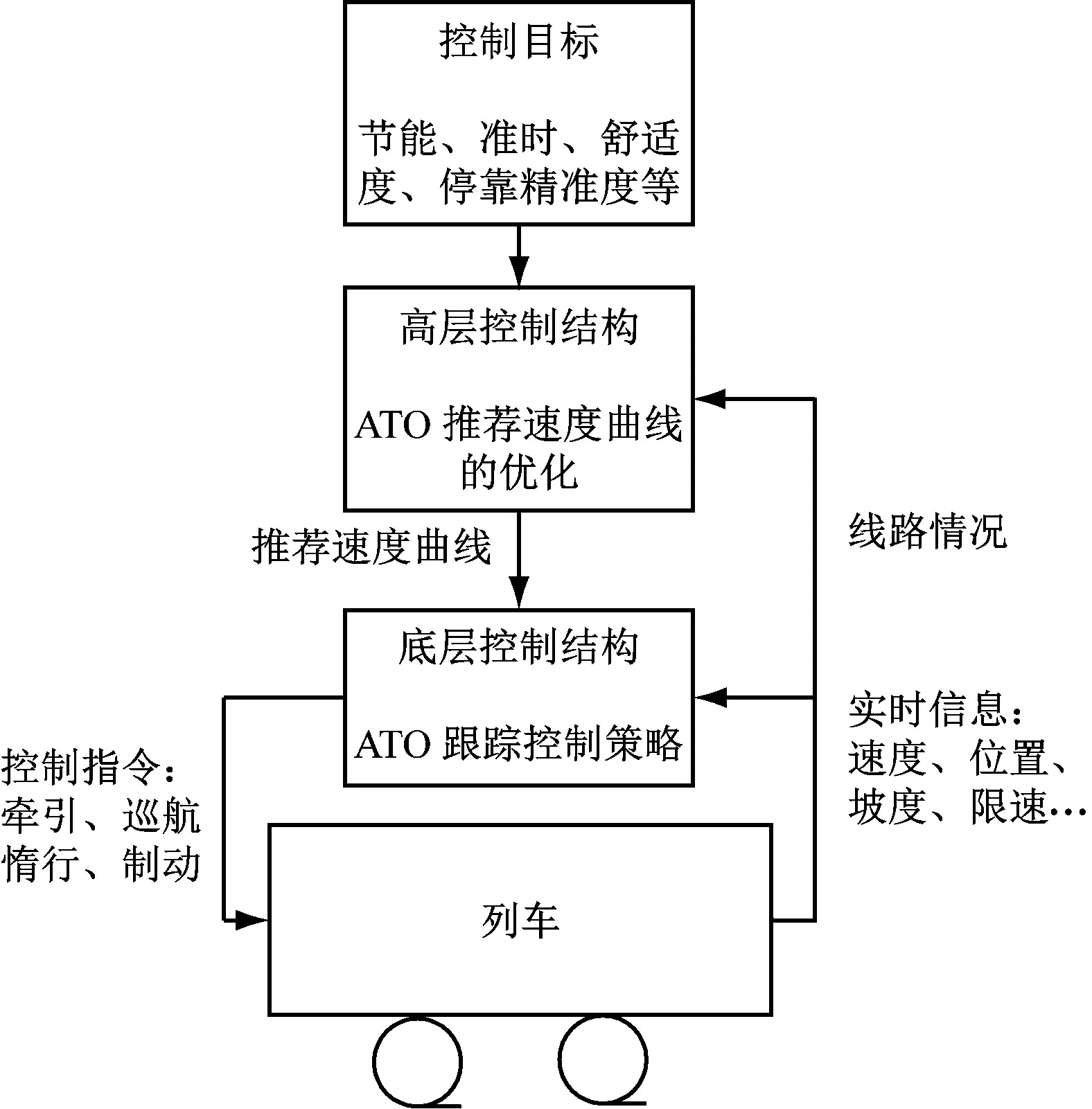
图1 ATO系统结构图

由图1可知，当通过ATO高层结构并采用相关的多种群遗传算法优化得到对应的列车推荐速度曲线以后，列车按照ATO底层结构追踪曲线运行。如果追踪不够精准，那么列车实际的运行能耗依然会很大，所以推荐速度曲线的优化与追踪这两个环节紧密相连，必不可少。本文采用PID控制器对列车推荐速度曲线进行追踪，控制器的传递函数表达式如式(3)所示。

(3)

式中：

Gc——控制器传递函数；

Kp——比例增益；

Ki——积分时间常数；

Kd——微分时间常数；

s——s域。

由式(1)经过推导线性化后的列车模型状态空间表达式如式(4)所示。

(4)

式中：

M——列车质量；

b——戴维斯参数；

本文将基于式(4)设计ATO的速度控制器，以达到按照算法优化后的列车推荐速度曲线对列车进行精确跟踪。

2 多种群遗传算法

2.1 采用遗传算法求解的必要性

列车推荐速度曲线优化算法常采用遗传算法、蚁群算法、粒子群算法、禁忌搜索等智能算法。应用最广泛、技术最成熟的智能算法是遗传算法。遗传算法因其具有隐含并行性，计算速率更快。此外，遗传算法还具有较好的可移植性，在遗传操作过程中不容易受到外部条件的制约。

2.2 多种群遗传算法与普通遗传算法的对比

遗传算法虽然有很多优点，但仍然存在以下问题：

1) 遗传算法中的选择操作直接由适应度决定，因此当种群中某些个体适应度较大时，很容易被多次选中，这会导致种群丧失多样性、种群进化停滞。

2) 遗传算法中的变异概率和交叉概算的选择决定了算法的收敛能力，如果只是单独地确定一个值，很难综合算法的收敛速度和收敛能力。

针对上述问题，本文采用多种群遗传算法。多种群遗传算法能够弥补遗传算法的上述缺陷，针对性解决遗传算法存在的问题。

1) 对于适应度，考虑采用多个指标，且每个指标的权重在某一区间内变化，以保证种群的多样性。

2) 对相关遗传算子赋予不同的参数，并采用多个种群并行搜索的方法，既能够达到不同的搜索目的，又能够加快算法的收敛速度和收敛能力。

多种群遗传算法结构示意图如图2所示。其操作方式是：首先建立多个种群，每个种群所采用的遗传算子取值各不相同；然后通过移民算子将多个种群联系起来，达到信息互换、协同进化的效果。这样便使得交叉概率及变异概率等的取值是一个范围，而不是固定值，从而很好地平衡了遗传算法的局部搜索能力和全局搜索能力。

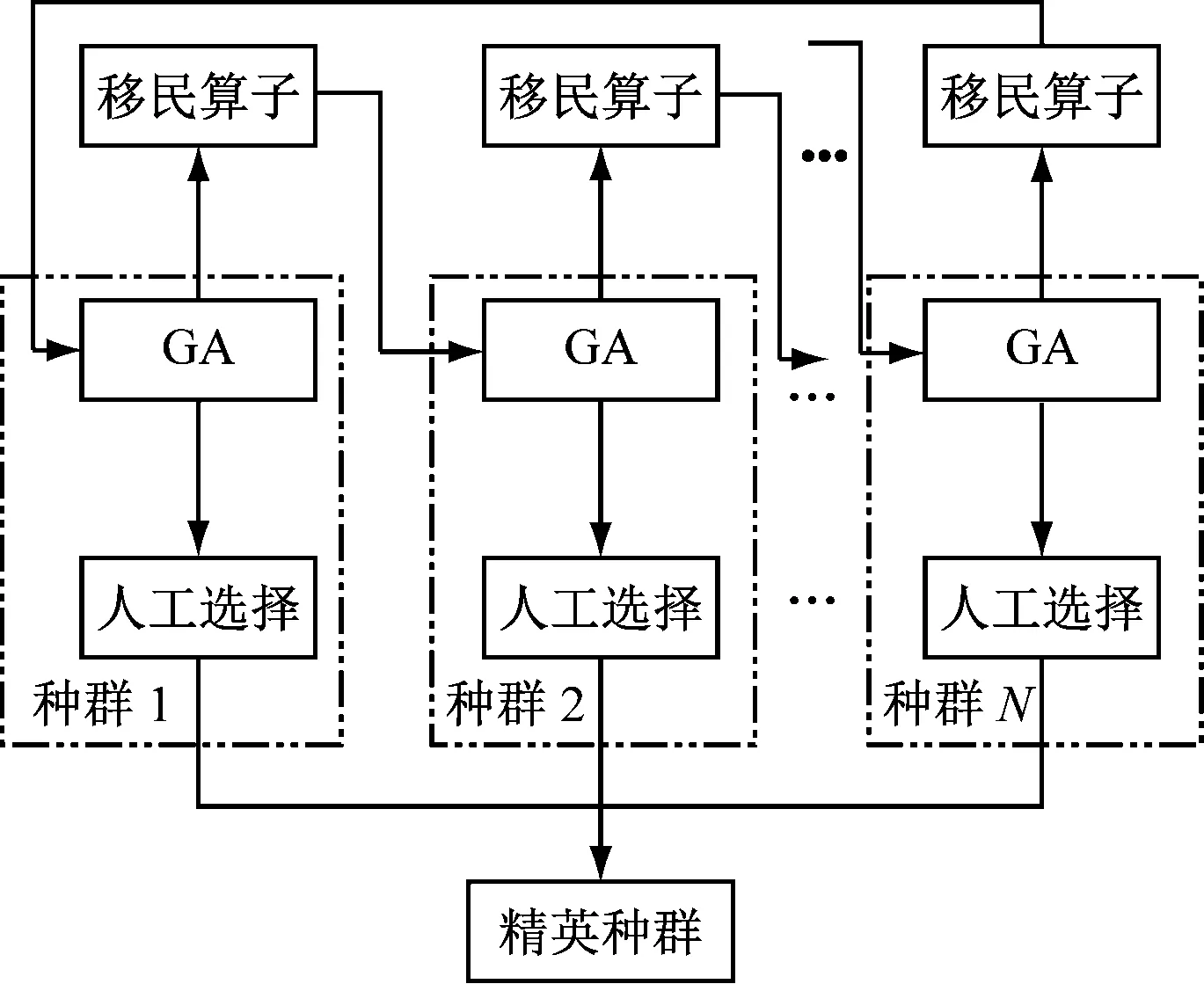
注：GA——遗传算法

2.3 选择算子对进化过程的影响

在其他遗传算子取值相同的前提下，选择算子取值分别为0.75、0.85、0.95时,算法的适应度函数同算法的进化代次数间的关系如图3所示。

由图3可知，当选择算子取值为0.75时，遗传算法收敛大约需要28代；当选择算子取值为0.85时，遗传算法收敛大约需要26代；当选择算子取值为0.95时，遗传算法收敛大约只需要10代。由此可知，在其他参数不变的情况下，选择算子取值的增大，对遗传算法的收敛速率有加速作用。基于仿真结果，本文交叉概率的取值为[0.85,0.90]。

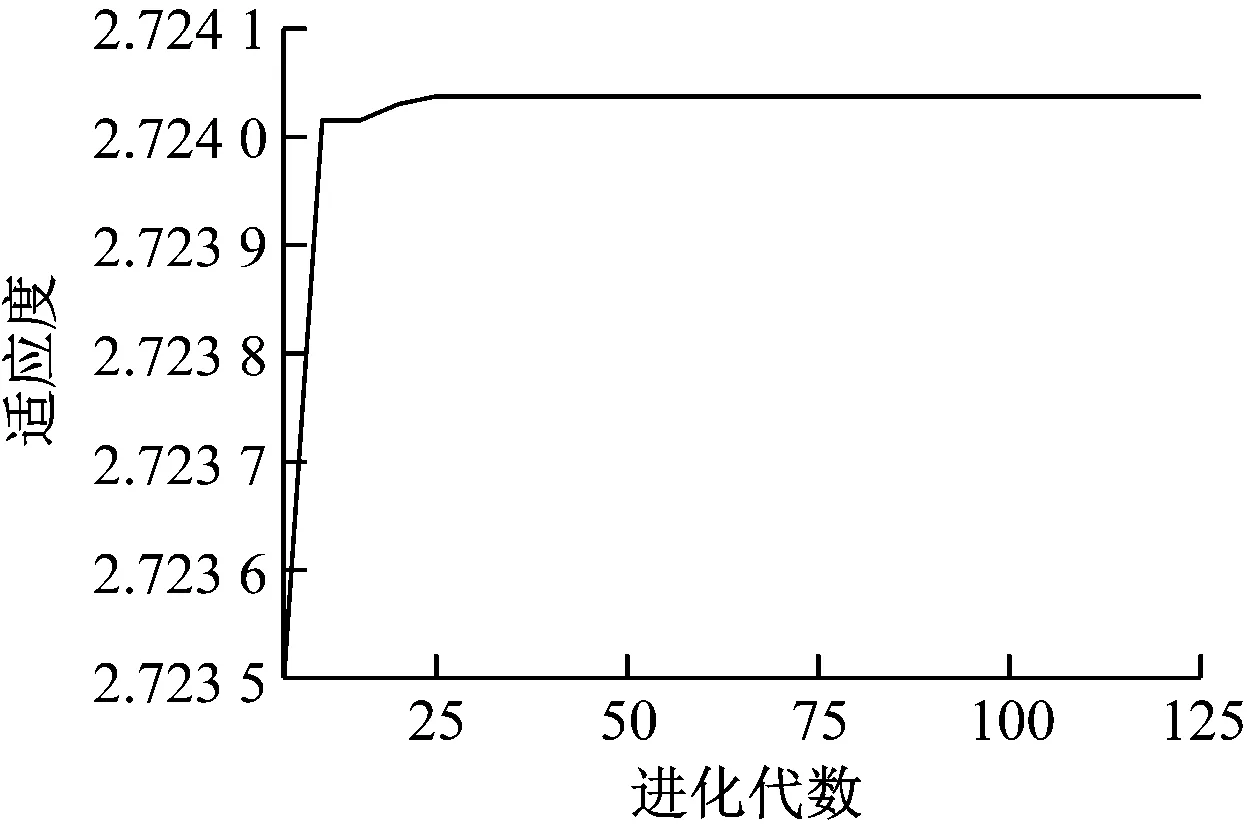
a) 遗传算子取值为0.75

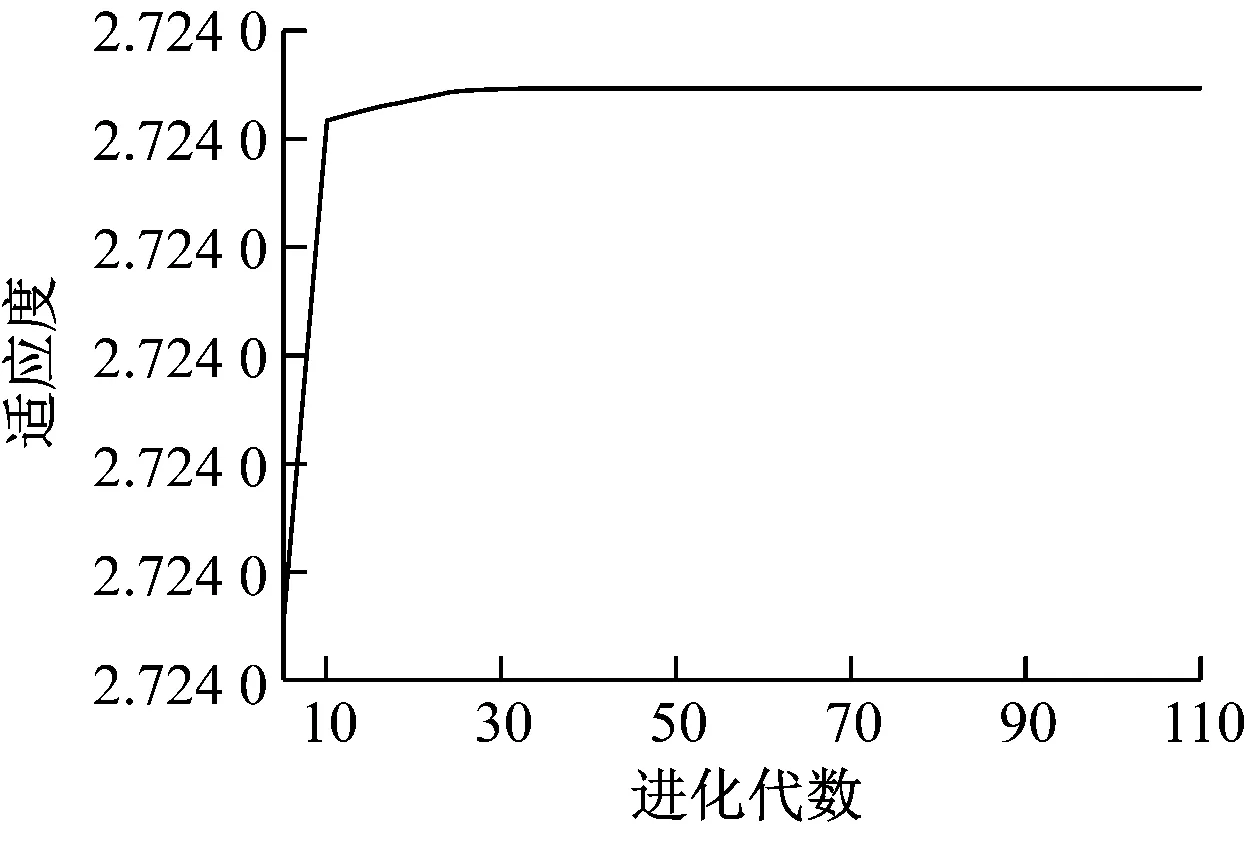
b) 遗传算子取值为0.85

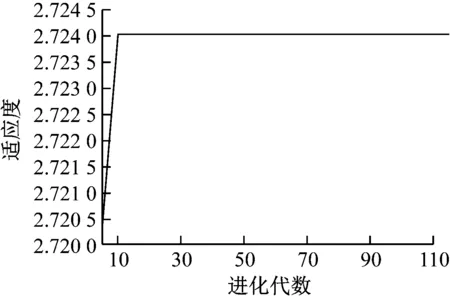
c) 遗传算子取值为0.95

2.4 交叉算子对进化过程的影响

在其他遗传算子取值相同的前提下，交叉算子的取值分别为0.7、0.8、0.9时,算法的适应度函数同算法的进化代次数间的关系如图4所示。

由图4可知，当交叉算子取值为0.8时，算法的适应度值更加接近最优适应度取值；当交叉算子取值为0.9时，算法的适应度值逐渐偏离最优适应度取值。由此可知，在其他参数不变的情况下，交叉算子的取值既不宜过大，也不宜太小。基于仿真结果，本文交叉算子的取值为[0.75,0.90]。

2.5 变异算子对进化过程的影响

在其他遗传算子取值相同的前提下，变异算子的取值分别为0.003、0.004、0.005时,算法的适应度函数同算法的进化代次数间的关系如图5所示。

由图5可知，当变异算子取值为0.003时，算法收敛大约需要7代；当变异算子取值为0.004时，算法收敛大约需要8代；当选择算子取值为0.005时，算法收敛大约需要15代。由此可知，在其他参数不变的情况下，选择算子的取值增大，对算法的收敛速率有减速作用。基于仿真结果，本文变异算子的取值为[0.004 5,0.006 5]。

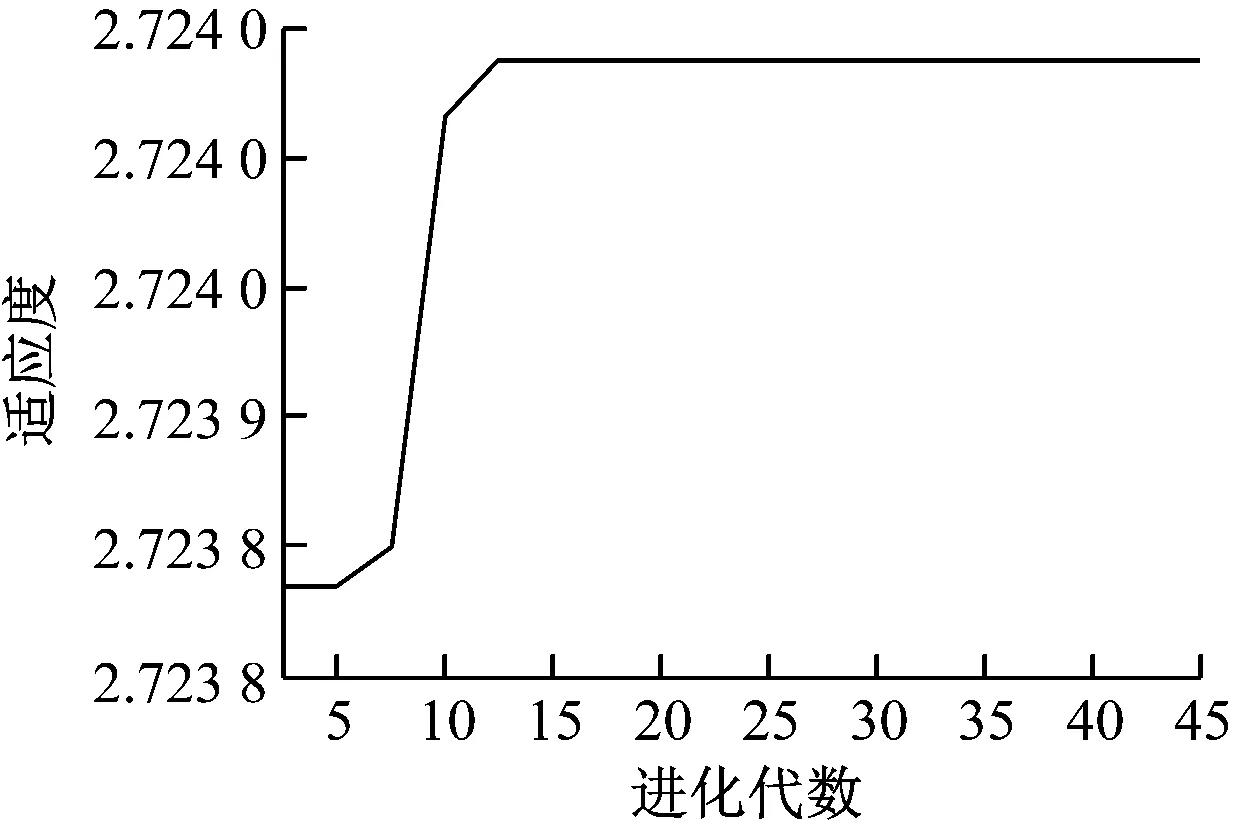
a) 交叉算子取值为0.7

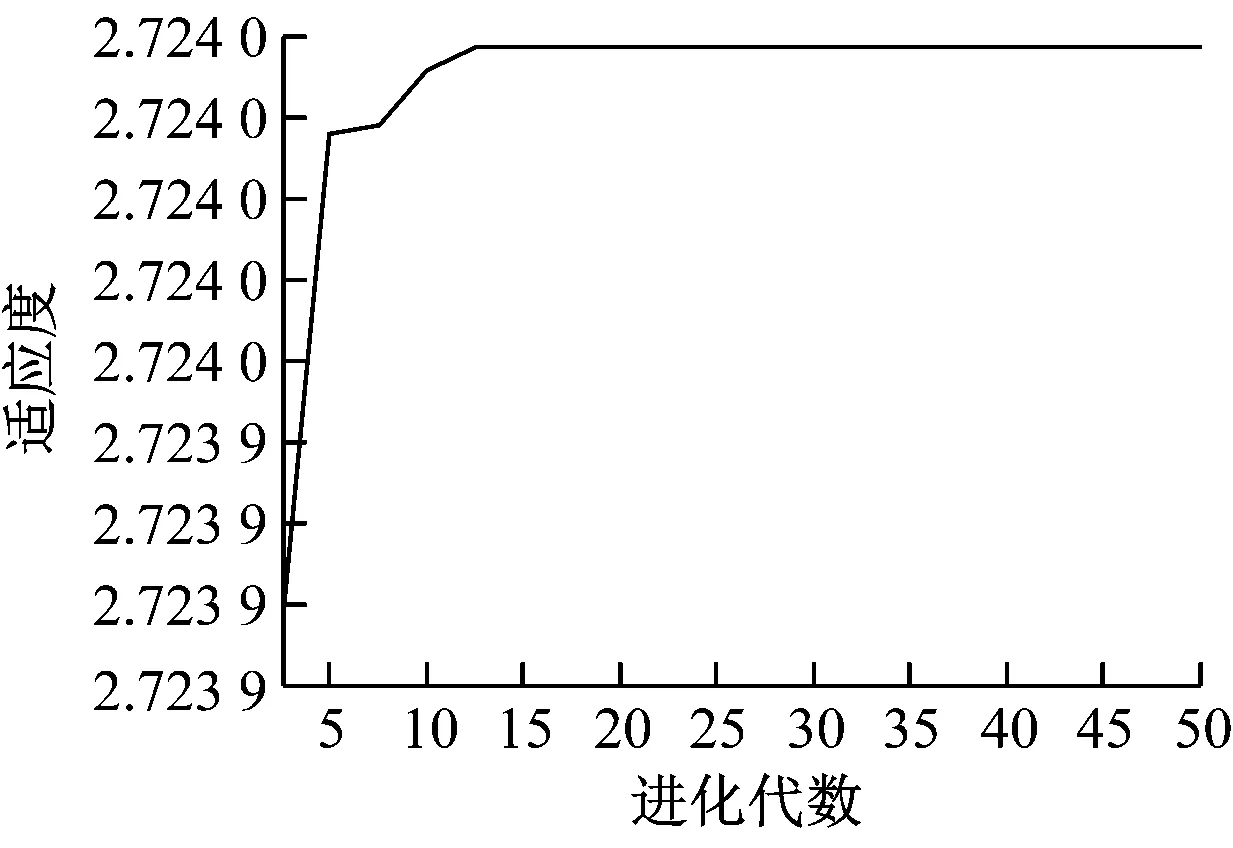
b) 交叉算子取值为0.8

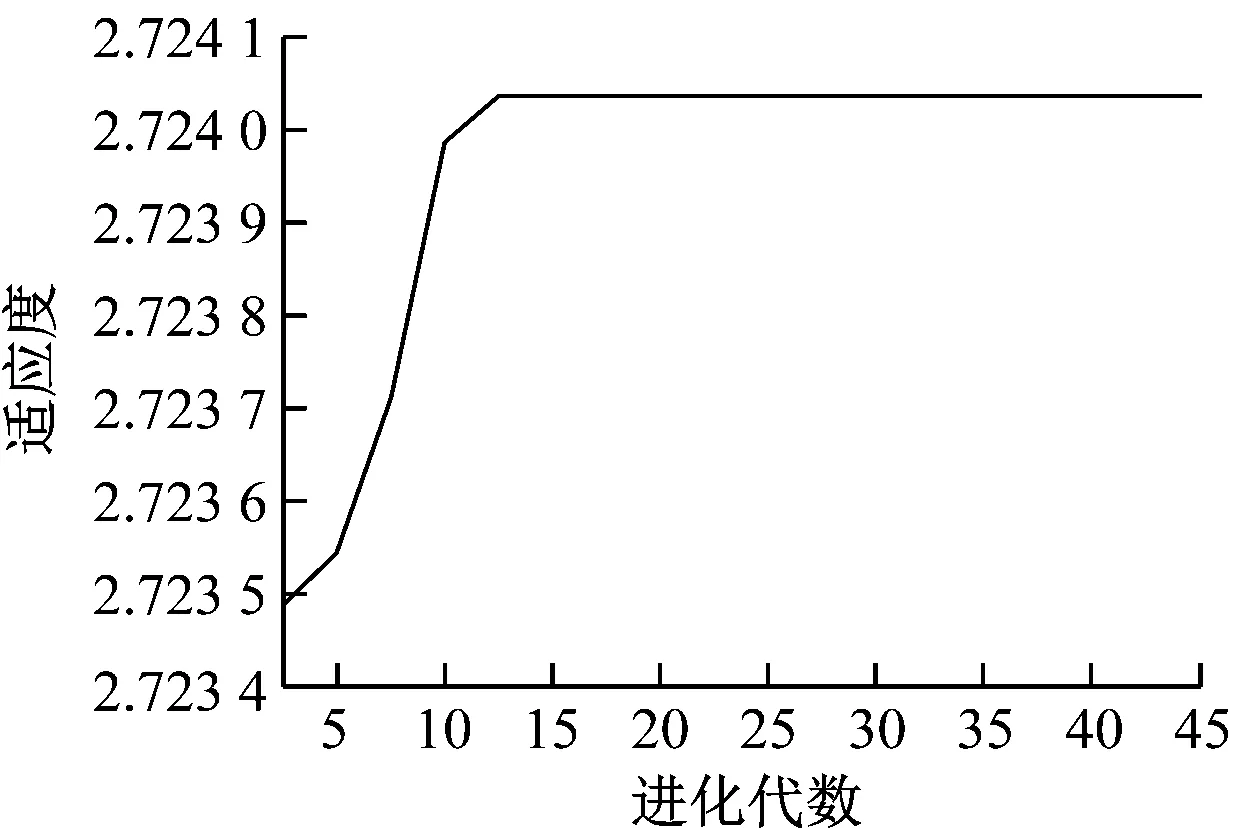
c) 交叉算子取值为0.9

3 仿真分析

3.1 仿真参数的设定

3.1.1 线路参数设定

本文选取北京地铁亦庄线的亦庄火车站站至次渠站进行仿真验证，线路参数及其取值见表1。

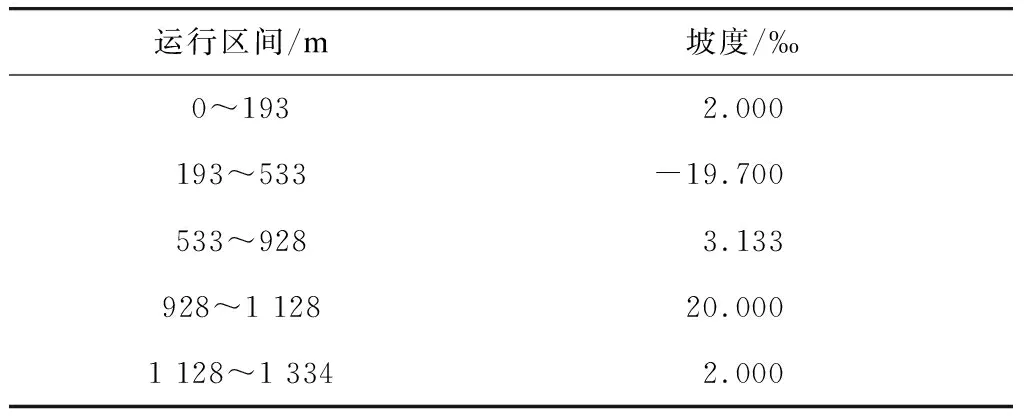
表1 北京地铁亦庄线的亦庄火车站站至次渠站的线路参数及其取值

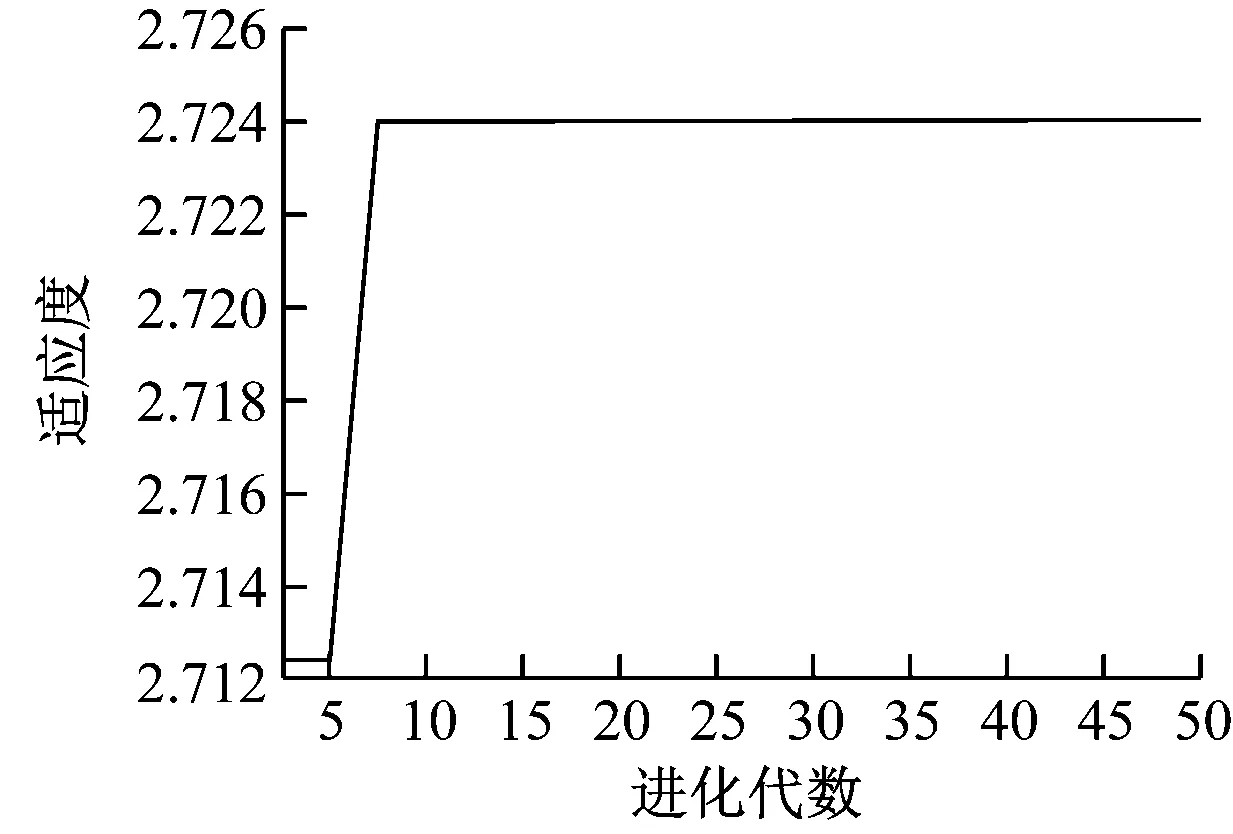
a) 变异算子的取值为0.003

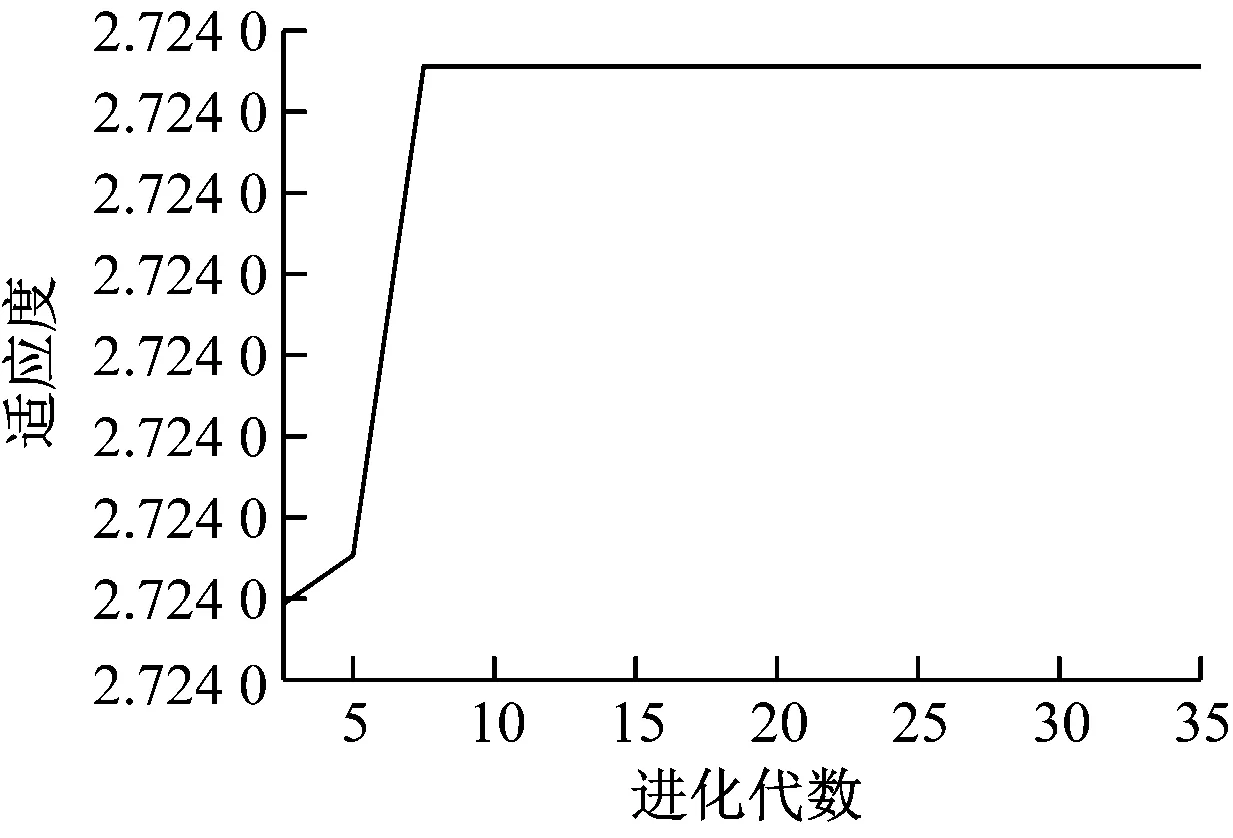
b) 变异算子的取值为0.004

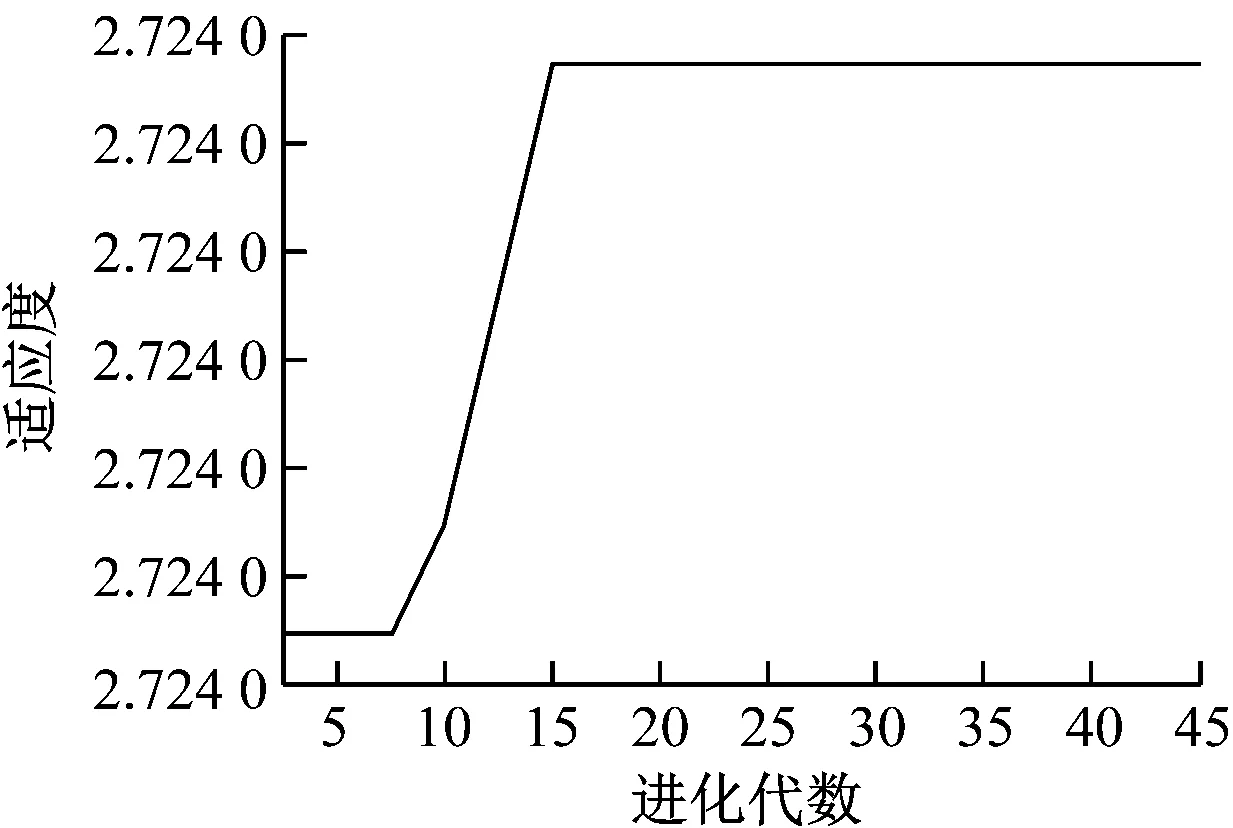
c) 变异算子的取值为0.005

3.1.2 车辆参数设定

式(5)为列车的最大牵引力Fmax计算公式。

(9)

式(6)为列车的最大制动力Bmax计算公式。

(10)

3.2 仿真系统架构

本文采用基于MATLAB软件的仿真系统，其总体架构如图6所示。该仿真系统主要包括参数输入模块、列车牵引模块、ATO控制器模块和结果输出模块。

3.3 多种群遗传算法的仿真分析

为验证本文所提运行节能策略的有效性，选取北京亦庄线亦庄火车站站至次渠南站进行仿真验证。选择算子的取值范围为[0.85,0.90]，交叉算子的取值范围为[0.75,0.90]，变异算子的取值范围为[0.004 5,0.006 5]。采用本文提出的适应度衡量指标模型，仿真结果如图7所示。

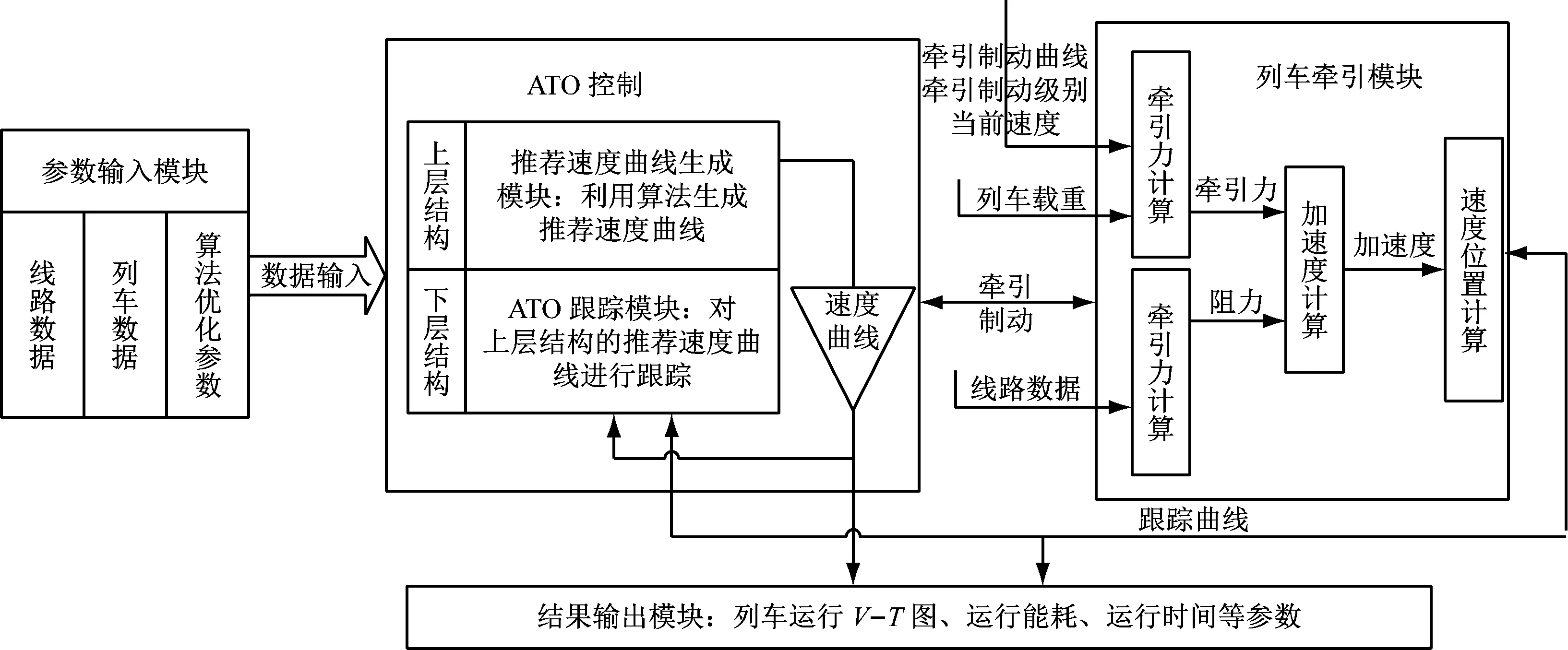
图6 仿真系统总体架构图

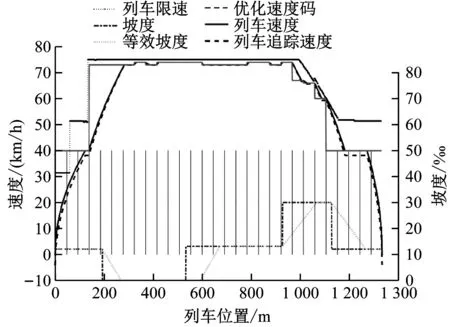
图7 采用多目标遗传算法的优化结果

多种群遗传算法显示PID跟踪得到的列车实际运行能耗为13.98 kW·h，运行时间为111.76 s。北京地铁的实际运行能耗为15.67 kW·h。与实际相比，本文所提列车运行节能策略可以节约10.78%的能耗。

4 结语

分析了不同遗传算子对多种群遗传算法的影响，确定了各遗传算子选取的原则及最优取值范围。通过建立适应度衡量指标模型，在综合考量运行列车的能耗、运行时间等多个指标的基础上给出了基于多种群遗传算法的列车节能策略。建立了基于MATLAB软件的列车运行仿真系统，验证了本文提出的列车节能策略的有效性。仿真结果表明，本文所提运行节能策略相较于目前实际运行能耗，可以节约10.78%的能耗。