基于瞬时边界元的轨道交通高架槽形梁桥声辐射特性及影响分析
2019-08-21彭思源
张 燕 彭思源
(华东交通大学土木建筑学院,330013,南昌//第一作者,副教授)
列车过桥时引起的声辐射问题一直是国内外学者关注的热点,人们对这个问题进行了较为系统的研究,取得了一定的成果。文献[1]采用有限元-边界元法对高速铁路U型梁进行了数值模拟和试验分析。文献[2]采用时域边界元法对轨道交通荷载作用下的钢连续梁振动产生的瞬态噪声场进行了试验分析和数值模拟。文献[3-4]结合边界元与统计能量分析法对32 m长混凝土简支梁的结构噪声进行理论与试验研究。文献[5]通过车桥耦合动力学理论结合间接边界元法研究了高速铁路32 m长简支槽形梁结构噪声的声辐射特性。
文献[6]采用模态叠加法分析了桥梁的结构噪声,研究表明:增加底板的厚度可以降低梁底的结构噪声。但是,文献[7]研究发现:桥梁底板厚度的变化对桥梁各个板件的振动、噪声无明显影响。因此,板厚对槽形梁结构噪声的影响有待进一步分析研究。
本文以某拟建高架线路30 m的混凝土槽形梁为研究对象,基于SIMPACK软件和ANSYS软件联合协同仿真分析方法,建立了车桥耦合系统振动分析模型以及槽形梁结构声辐射有限元/边界元模型;在计算列车负载时槽形梁结构振动响应的基础上,采用瞬时边界元法,探讨了底板厚度对槽形梁结构噪声的影响。
1 轨道交通高架槽形梁声振分析模型
1.1 轨道交通高架槽形梁桥模型
某拟建槽形梁桥处于高架平坡线路段,下部结构采用T型桥墩,梁下净空大于4.5 m,为双线分离式槽形梁桥如图1所示。梁体两侧的腹板结构采用非对称形式,即其中一侧为弯弧形不等壁折腹式腹板(中、上段面隆鼓,平滑加厚),连接该侧腹板顶部的翼缘板选用T形翼缘板,即拥有内、外侧两个可兼做疏散平台的凸缘;梁体另外一侧腹板结构为弯弧形腹板(等壁腹板结构),该侧腹板的顶部采用7形翼缘板连接,即仅存在向内侧的凸缘。槽形梁桥的标准跨径为29.94 m,梁宽为5 m,高为1.8 m,底板厚度为0.28 m,腹板厚度为0.24 m,支座设在距梁端0.57 m处。
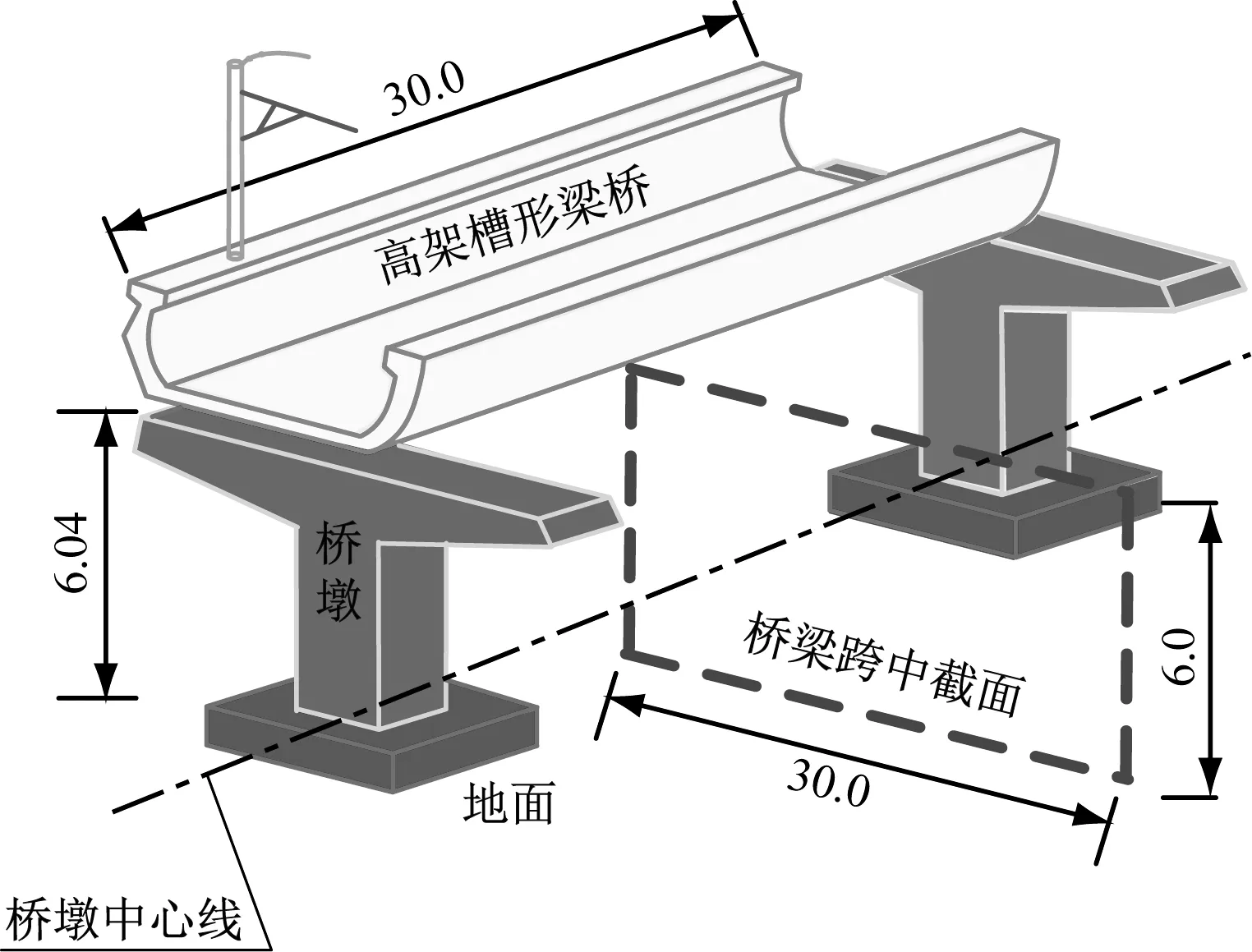
尺寸单位:m
图1 拟建高架槽形梁桥
1.2 轨道交通高架槽形梁有限元模型
基于有限元理论,建立轨道交通高架槽形梁模型。假设钢轨为能承受拉、压作用的纵向连续梁,其拉压刚度处处相等,且为常量;轨道板、底座板、CA砂浆层(砂浆层不开裂)都为“纵连”轨道结构,轨道板、底座、CA砂浆固结为一体能够承受外界拉、压作用;主要探讨槽形梁桥的结构噪声,故忽略桥墩的影响,在数值分析模型中桥墩的模拟采用线性弹簧模拟。
在分析模型中,将钢轨视为Euler梁,用梁单元模拟;槽形梁梁体、轨道板、CA砂浆层均用实体单元模拟,为避免病态网格的出现,采用体扫掠法划分将其划分为大小合适的六面体单元;连接钢轨与轨道板的扣件采用间距为0.625 m的离散弹簧阻尼单元模拟。主要结构参数见表1。
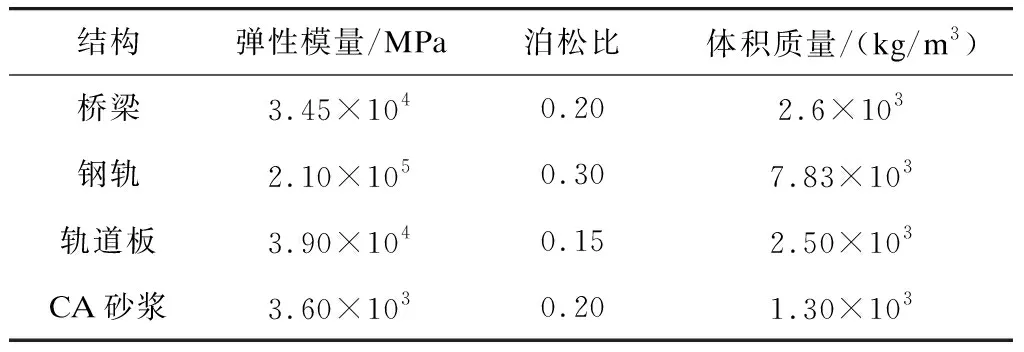
表1 槽形梁模型主要结构参数表
槽形梁的截面形式参照某拟建高架轨道交通选用的简支槽形梁设计图纸,其有限元模型如图2所示。各项模型参数经过多次调试,能满足GB 50157—2013《地铁设计规范》的要求。

图2 轨道交通槽形梁有限元模型
1.3 轨道交通槽形梁边界元模型
瞬时边界元法是基于有限元法求解的桥梁瞬态动力响应结构通过插值的方法分配到桥梁结构声学边界元网格上作为边界条件,然后求解出槽形梁的瞬态声辐射特性。
槽形梁的表面为封闭的边界表面,通过对其离散,可以得到边界元求解方程:
Ap(ra)=Bvn(ra)
(1)
式中:
A、B——系数矩阵;
p(ra)——封闭边界表面Ωa的声压;
vn(ra)——封闭边界表面Ωa的速度。
槽形梁表面外部无限域V内任意一点的声压p0(r)可以通过Helmholtz积分方程求得。
瞬时边界元法用于计算桥梁结构振动声辐射问题时,不仅能够反映声压在时间域的分布,并且能够合理反映列车荷载作用下桥梁辐射噪声情况,同时避免了采用模态叠加法时出现的模态截断误差,与稳态边界元相比,避免了对边界条件进行稳态简化,计算精度更有保障。
因此,基于瞬态边界元理论建立了槽形梁结构声辐射边界元模型如图3所示。在进行瞬态边界元分析计算时,边界元网格必须是三角形网格,故采用自由网格划分。

图3 轨道交通高架槽形梁边界元模型
1.4 车桥耦合模型
为了避免车桥耦合振动分析交叉迭代计算量较大的弊端,基于多体动力学理论,建立了精细化车桥耦合的空间动力学分析模型。地铁列车模型是在参照了国内地铁B型车的结构参数及动力学参数的基础上,做了一些合理简化,通过SIMPACK软件建立的。车辆模型的基本参数,见表2。每节地铁B型车一共考虑了34个自由度,其中,假定每节地铁B型车数值分析模型由1个车体、2个转向架、4个轮对等刚体组成。车辆刚体、转向架刚体考虑了伸缩、横摆、浮沉、点头、侧滚、摇头6个自由度,轮对考虑了4个自由度。轮对和转向架以及转向架和车体之间分别通过一系、二系弹簧连接,轮轨接触采用单点非线性弹性接触。

表2 地铁列车基本参数
通过多体动力学软件SIMPACK和有限元软件ANSYS分别建立了钢轨、扣件、轨道结构等的槽形梁桥有限元模型和包含了轮对、转向架、车体等部(构)件的多刚体系统列车车辆模型。将槽形梁桥有限元模型作为柔性体导入多体动力学软件SIMPACK中,同时,导入槽形梁桥模态分析和子结构分析的结果文件,利用SIMPACK软件中柔性轨道模块,实现列车模型和桥梁模型的共同求解。
其中,列车模型和槽形梁桥有限元模型作为两个系统,分别求解轮流迭代。通过轮轨接触之间的离散点实现车桥耦合模型之间位移、速度以及相互作用力的数据交换。此外,为了控制列车车辆系统和桥梁系统所有自由度的计算结果相对于前一迭代步的误差都不超过系统迭代控制误差精度的要求,文中控制精度取10-4。
2 轮轨激振力的获取和加载
基于车桥耦合模型,采用联合仿真法,获取轮轨激振力。采用地铁B型车6节编组模拟加载,计算速度为80 km/h,将列车实际运行过程简化为一系列随时间移动的集中力荷载,采用节点加载方式分析高架桥槽形梁桥的结构噪声辐射特性,每节车辆按轮对左右对称分布共8个集中力荷载,加载时间步长为0.005 s,加载方式如图4所示。
图4 轮轨激振力加载方式
3 结构噪声的影响参数分析
3.1 轨道交通高架槽形梁桥声辐射特性分析
将基于车桥耦合模型计算出来的轮轨激振力加载到轨道—槽形梁有限元模型上,进行槽形梁的瞬态动力响应分析,从而求得槽形梁桥的振动响应;随后在LMS平台的Virtual.lab声学软件中建立边界元模型,并将槽形梁桥有限元模型各节点的振动响应通过插值的方法导入到槽形梁桥声学边界元网格上作为边界条件,采用瞬时边界元法对轨道交通槽形梁结构噪声瞬时辐射特性进行预测分析。
图5、图6分别给出了列车以80 km/h的时速通过桥梁时的整个桥梁振动变化情况以及声场、声压的变化情况。其中图5为第一节列车刚上桥时槽形梁桥的振动情况,图6为第一节车第一个转向架位于桥梁跨中附近时刻槽形梁桥的振动与瞬时辐射噪声情况。
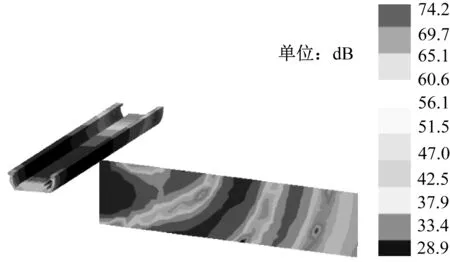
图5 0.65 s时刻桥梁振动变化云图
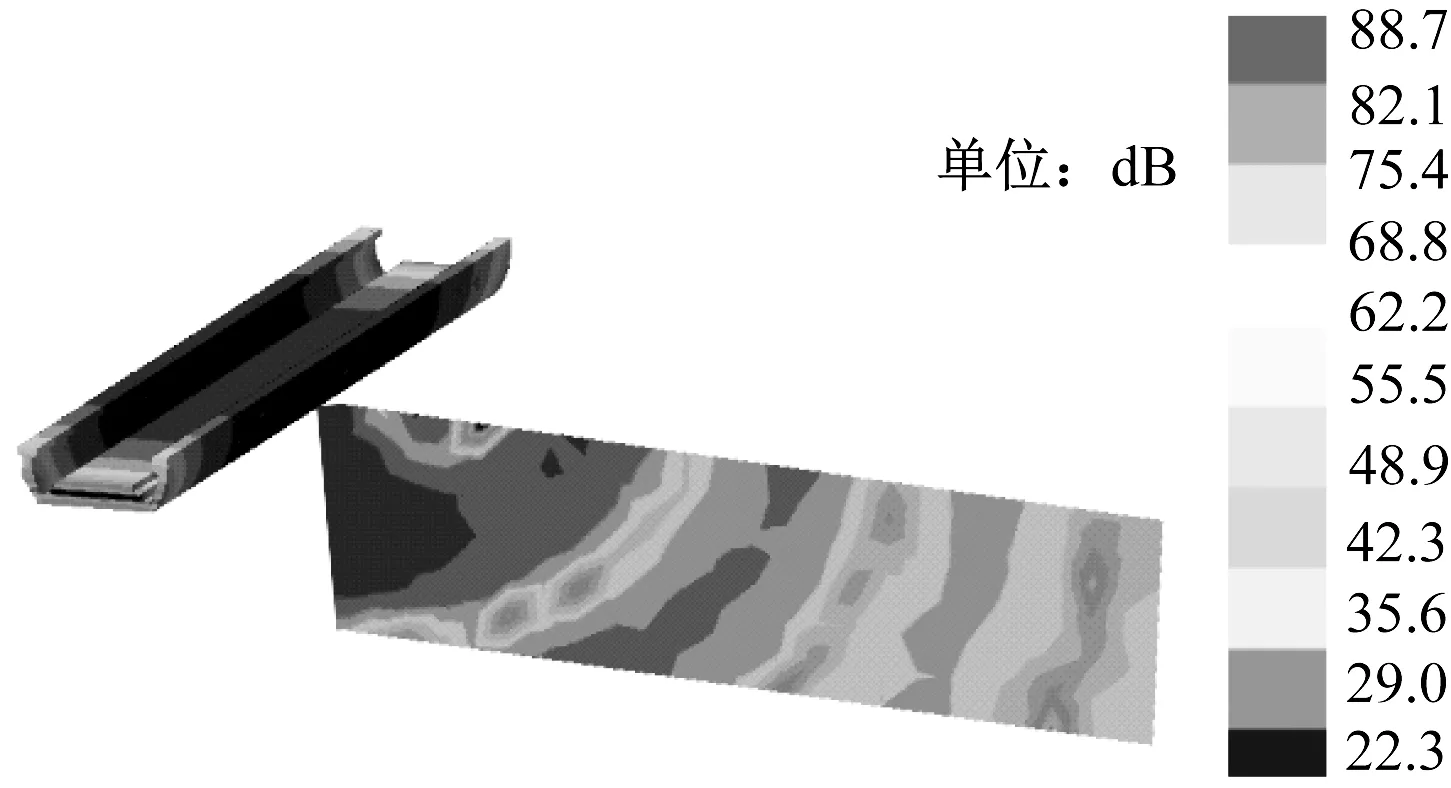
图6 2.7 s时刻桥梁振动变化云图
从图5、图6可知:列车以80 km/h的速度通过槽形梁的整个过程中,在任何位置、任何时刻的声压级都是一个迅速变化的量;跨中截面各个场点的瞬时声压级变化较大,但主要集中在槽形梁底板正下方;从总体上来看,距离线路中线越远,声压级越小,但也越发复杂,局部会出现声压级突变的区域。这一分析结果为槽形梁结构振动与辐射噪声问题的深入研究,提供了非常直观的可视化过程。
3.2 轨道交通槽形梁桥结构噪声影响分析
为了研究底板厚度对槽形梁桥结构辐射噪声的影响,分别选取梁体正下方距离地面1 m的声学场点1作为近声场考察点,距离线路中心线25 m,且距地面1 m的声学场点2作为远声场考察点进行分析,如图7所示。
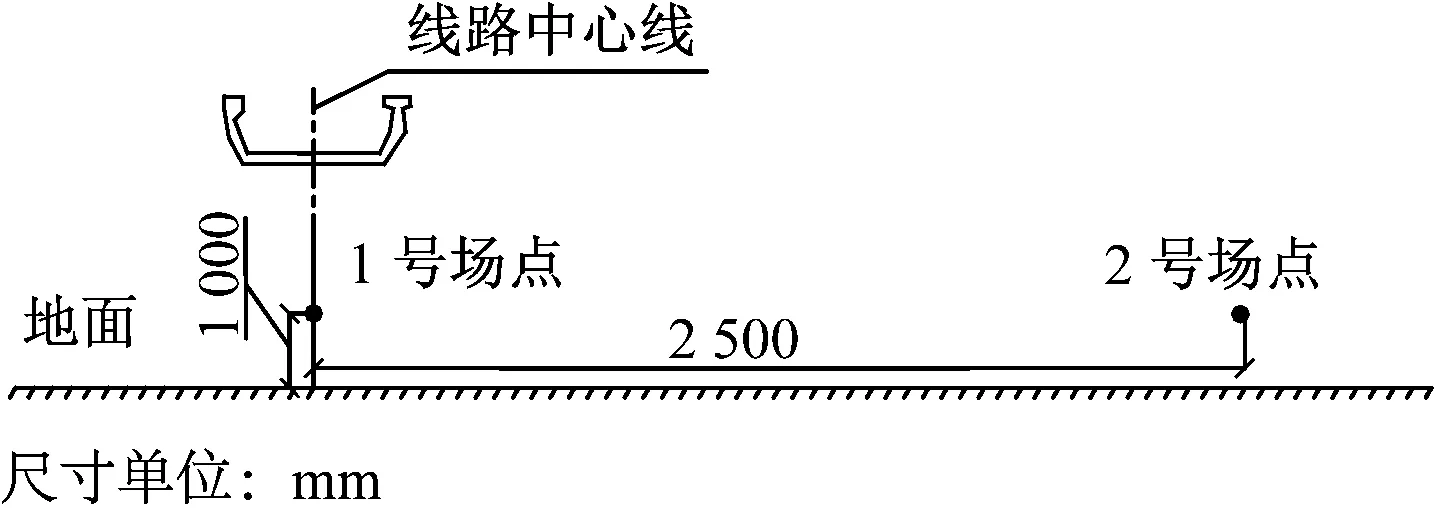
图7 声学场点分布
以跨径30 m槽形梁为标准模型,通过改变底板厚度,得到其他模型。槽形梁结构如图8。其板件厚度和高度满足《混凝土结构构造手册》的要求[8]。
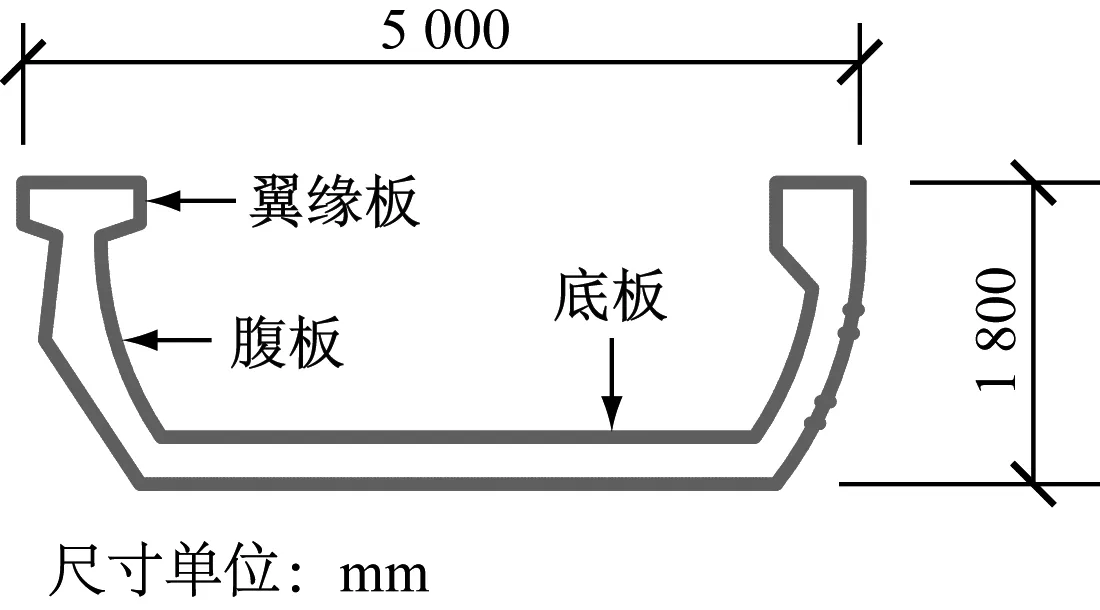
图8 槽形梁结构截面示意图
图9、图10分别给出了近声场、远声场考察点的瞬时声压辐射情况。对比分析图9、图10可知,编组列车在最后一节车到达桥梁跨中时,结构瞬时辐射噪声出现最大值;高架槽形梁桥底板厚度的增加对梁体正下方的近声场具有较好的降噪效果,最大瞬时声压降低约5 dB,但并非越厚越好,据表3可以发现,当底板厚度从0.32 m增大到0.34 m时,出现瞬时辐射噪声放大现象;增加底板厚度对结构远声场有一定程度的影响,但不明显。
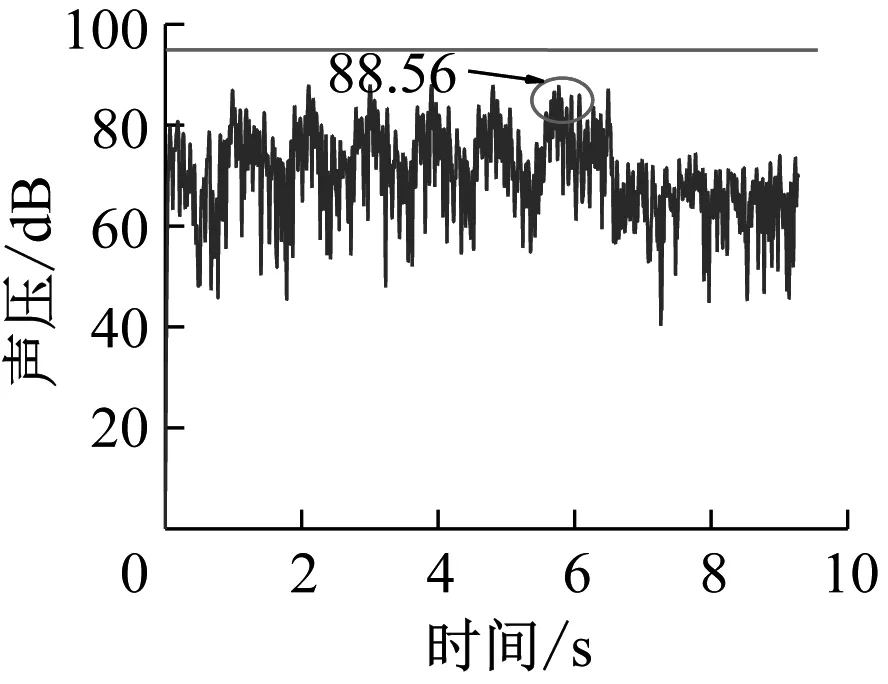
a) 底板厚度为0.28 m
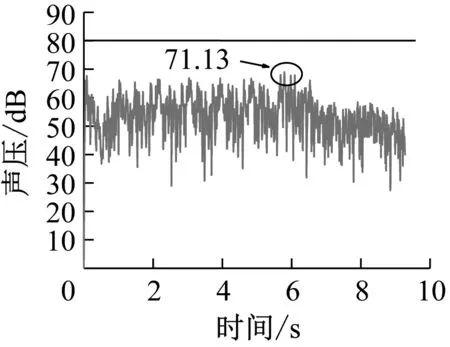
a) 底板厚度为0.28 m
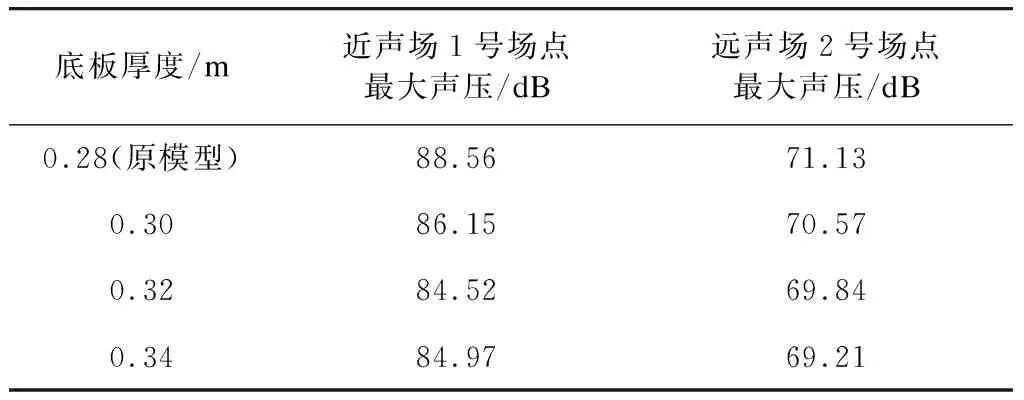
底板厚度/m近声场1号场点最大声压/dB远声场2号场点最大声压/dB0.28(原模型)88.5671.130.3086.1570.570.3284.5269.840.3484.9769.21
4 结论
1) 列车以80 km/h的速度通过槽形梁的整个过程中,在任何位置、任何时刻的声压级都是一个迅速变化的量。
2) 轨道交通槽形梁结构噪声主要集中在底板附近,针对槽形梁桥采取减振降噪措施时,可优先考虑桥梁底板结构。
3) 距离线路中线越远,声压级越小,但也越复杂,局部会出现声压级突变的区域。
4) 高架槽形梁桥底板厚度的增加对梁体正下方的近声场具有较好的降噪效果;对结构远声场,有一定程度的影响,但并非越厚越好,其最佳值有待进一步确定。
