跨坐式单轨车辆转向架构架疲劳寿命预测研究
2019-08-21杜子学
杜子学 马 帅 杨 震 唐 飞 李 耀
(重庆交通大学机电与汽车工程学院,400074,重庆//第一作者,教授)
转向架构架作为跨坐式单轨车辆的承载基础,不仅应具有足够的刚度和强度,而且还应有满足要求的疲劳强度。构架在复杂的交变载荷作用下极易形成疲劳裂纹,威胁列车的运行安全。
对跨坐式单轨转向架构架进行疲劳寿命预测,最合适的方法是名义应力法。名义应力法以材料或构件的应力—循环寿命曲线为基础,应用载荷计数统计方法和疲劳损伤累积理论评估试样或构件的疲劳寿命[1]。
1 转向架构架有限元模型建立
转向架主要由厚度和大小不同的薄板组装焊接而成,因此采用四边形单元为主,三角形单元为辅的板壳单元对构架进行网格划分[2]。转向架构架有限元模型如图1所示。
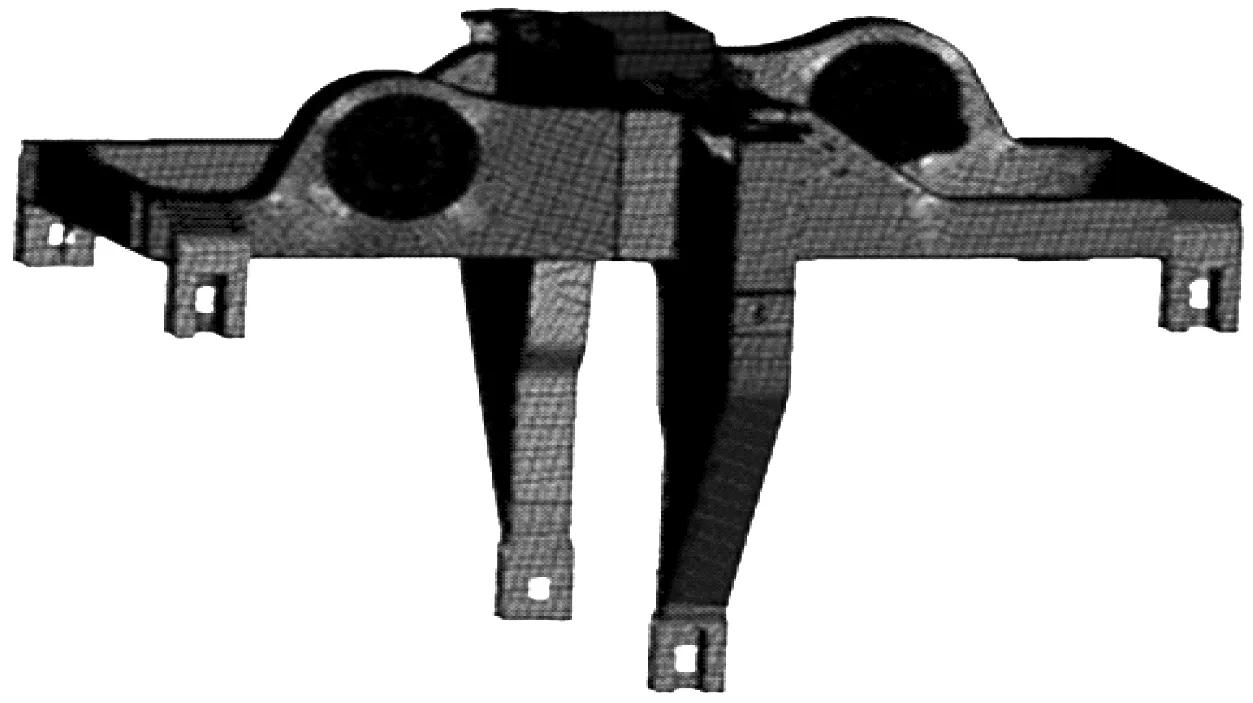
图1 转向架构架有限元模型
2 转向架构架单位载荷静强度分析
转向架构架疲劳寿命分析考虑的是满载直线匀速工况,采用Hyperworks软件对其满载直线匀速工况进行有限元计算,得到Von Mises应力最大值为154.4 MPa,位置在侧梁内部加强筋与侧梁内板焊缝连接处,其应力最大值小于材料Q 345D的屈服强度345 MPa。
采用准静态载荷叠加法,把转向架构架各载荷输入点处的单位载荷下的应力计算结果叠加起来,作为转向架构架疲劳寿命分析的有限元应力分析结果输入。在Hypermesh软件中建立关联点耦合空气弹簧座的安装面,将垂向载荷以集中力的形式施加到对应的关联点上,使用这种加载方式可以使集中载荷均匀分布在与关联点相耦合的面上。在左右空气弹簧、左右导向轮、前后车轴和导向轮等单独加载单位载荷通过惯性释放进行有限元计算,得到了典型工况下的应力分布情况。前车轴单位载荷应力分布云图如图2所示。
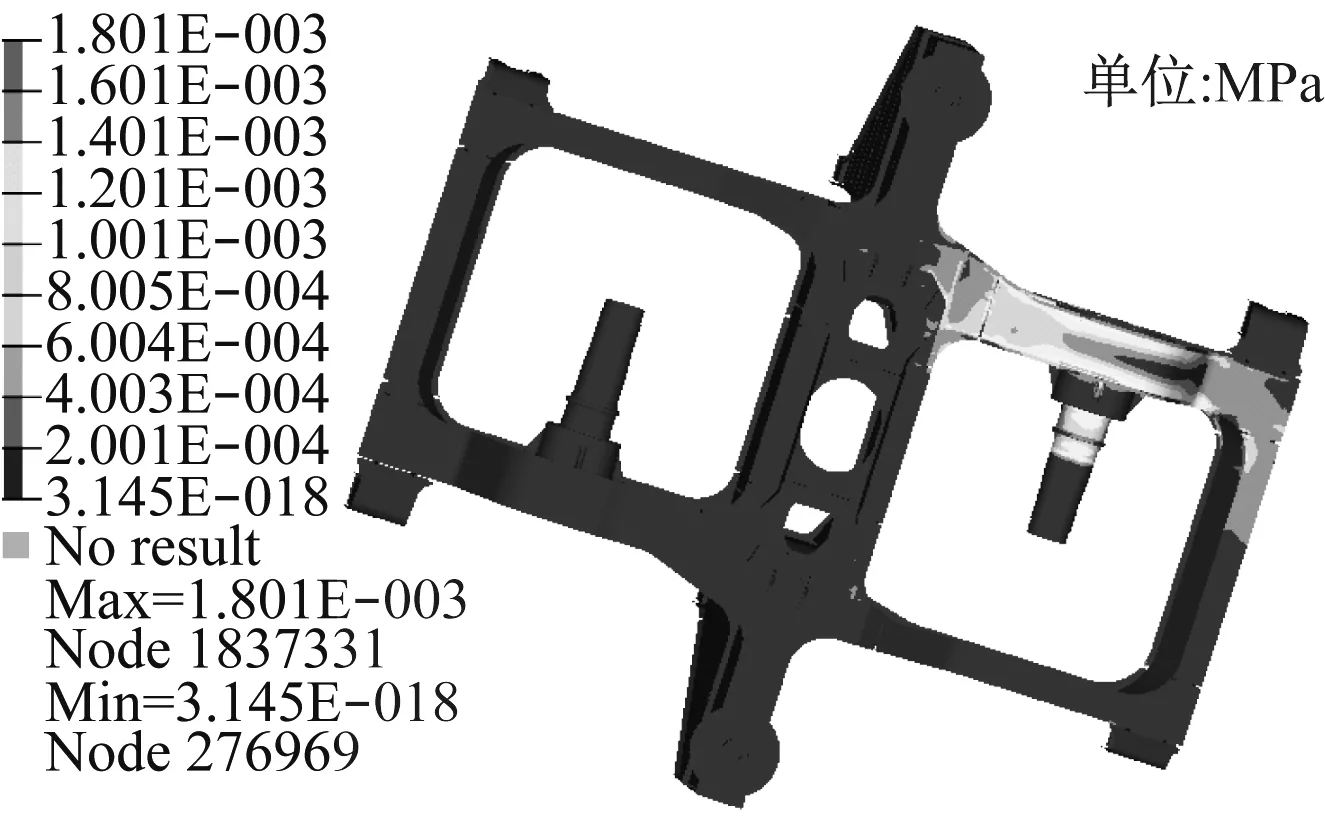
图2 前车轴单位载荷应力分布云图
3 转向架构架疲劳分析用载荷
由于实车试验条件的限制,以及转向架构架车轴和空气弹簧座主要承受垂向载荷,因此,试验只测量了车轴和车体的垂向加速度时间历程,通过在车轴和空气弹簧座施加垂向载荷时间历程计算疲劳寿命。
3.1 仿真载荷时间历程的获取
采用多体动力学方法,利用Adams软件,建立单轨车辆动力学仿真模型。将轨道走行面设定为A级路面,通过轮轨耦合动力学分析,获得车速60 km/h、满载直线行驶工况下,5~30 s时间内的转向架左右空气弹簧座垂向、左右导向轮、左右稳定轮、前后走行轮上的载荷时间历程。图3为左空气弹簧和右空气弹簧的载荷时间历程。
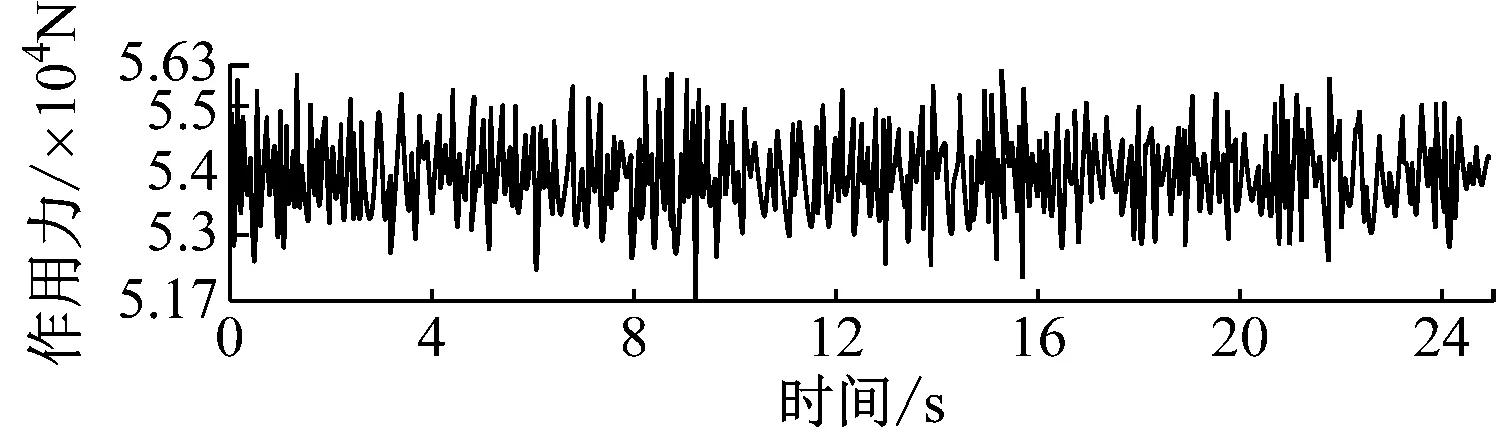
a) 左空气弹簧载荷时间历程
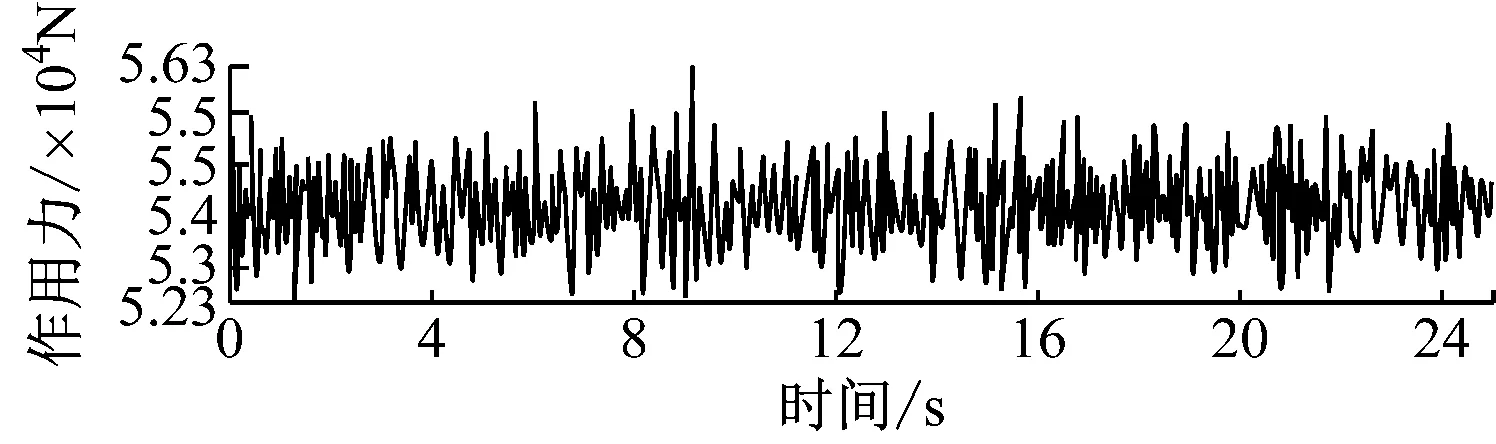
b) 右空气弹簧载荷时间历程
3.2 试验载荷时间历程的测取
试验在单轨线路上进行,车辆载荷模拟为AW3(满座+9人/m2超常载)状态。试验采用加速度传感器,分析处理采用IMC-CRSL-02-NET采集仪。
3.2.1 加速度时间历程测取
在车厢中加载11.4 t沙袋,试验获得了60 km/h转向架构架车轴和车体满载的加速度,采样频率为2 000 Hz,灵敏度系数车体地板为-1 000 Hz,转向架车轴为-20 Hz。图4分别为前车轴、后车轴和车体的垂向加速度历程。
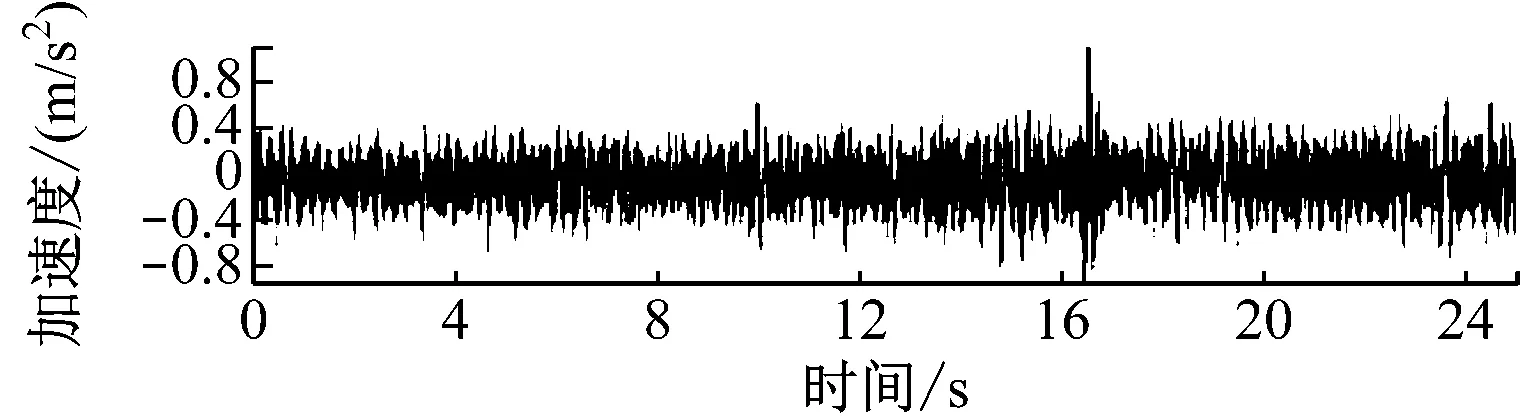
a) 前车轴垂向加速度历程
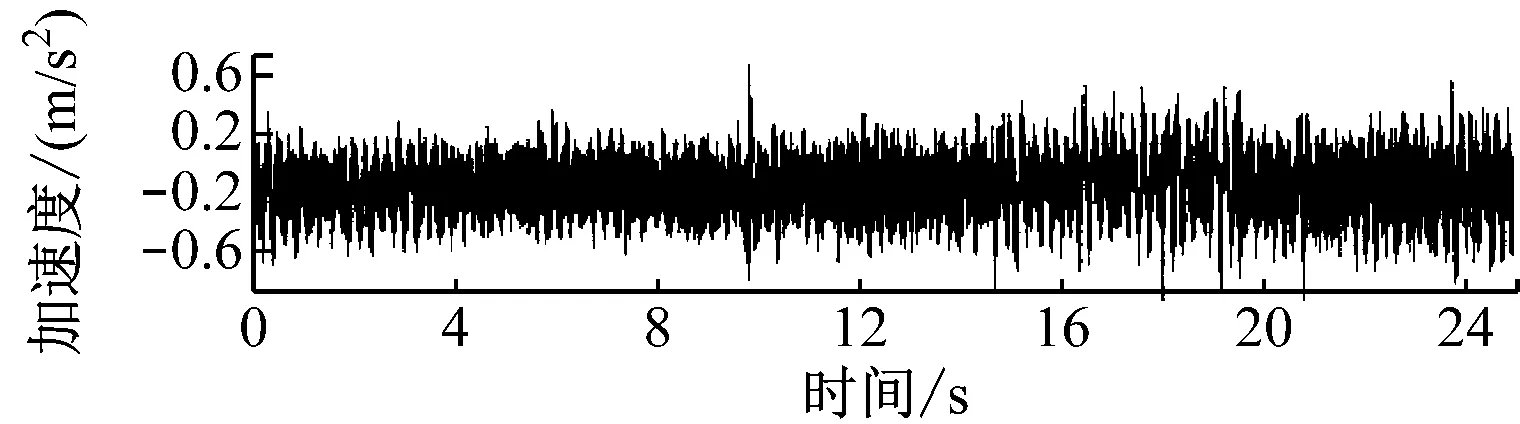
b) 后车轴垂向加速度历程
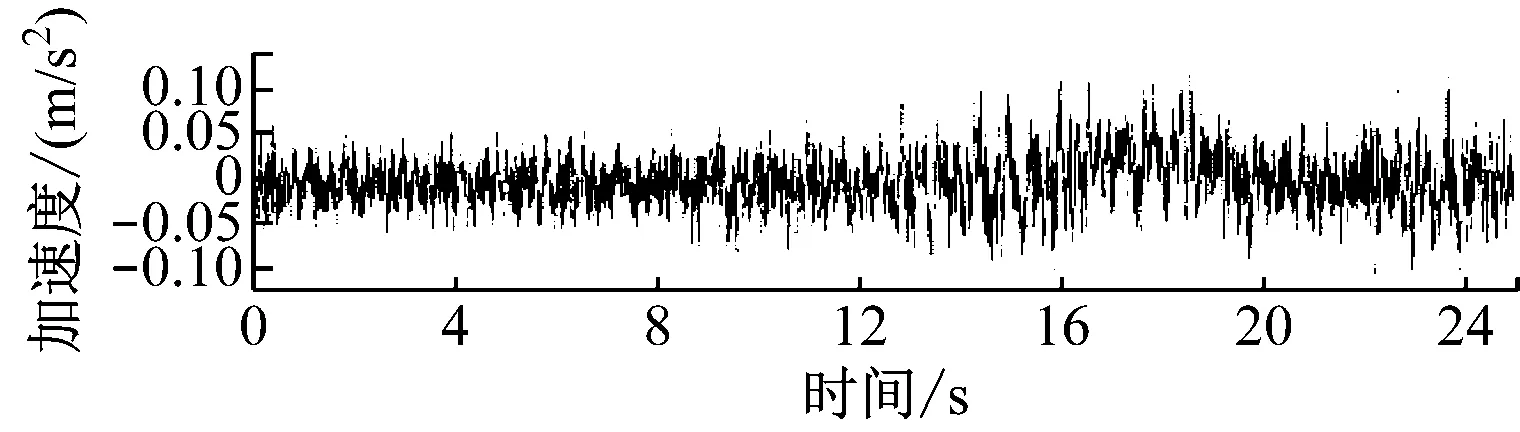
c) 车体的垂向加速度历程
3.2.2 载荷时间历程的处理
基于有限元软件计算疲劳寿命的方法有两种,一种是通过约束车轴的6个自由度,在空气弹簧上施加垂向载荷时间历程;另一种是基于Ncode软件计算方法,同时在车轴和空气弹簧座上施加垂向载荷时间历程,通过惯性释放的方法来计算疲劳寿命[3]。该试验采用基于Ncode软件计算方法计算转向架构架的疲劳寿命。
通过加速度与合外力的关系,用车轴和空气弹簧所受载荷除以重力加速度,模拟车轴质量和空气弹簧座质量。将加速度时间历程转换为载荷时间历程的公式如下:
(1)
式中:
FK1——左空气弹簧座载荷;
FK2——右空气弹簧座载荷;
nk——空气弹簧数量;
mc——满载时车体质量;
g——重力加速度;
ac——车体加速度。
(2)
(3)
Fz1——前车轴载荷;
Fz2——后车轴载荷;
nz——车轴数量;
mz——车轴质量;
g——重力加速度;
az1——前车轴加速度;
az2——后轴加速度。
得到的载荷时间历程谱如图5所示。
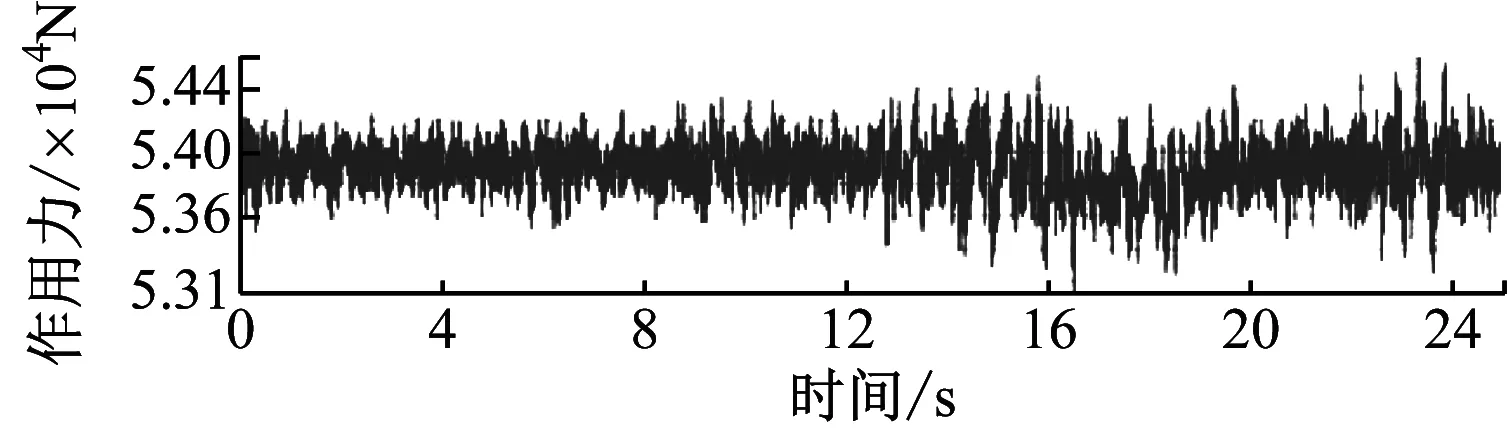
a) 左空气弹簧
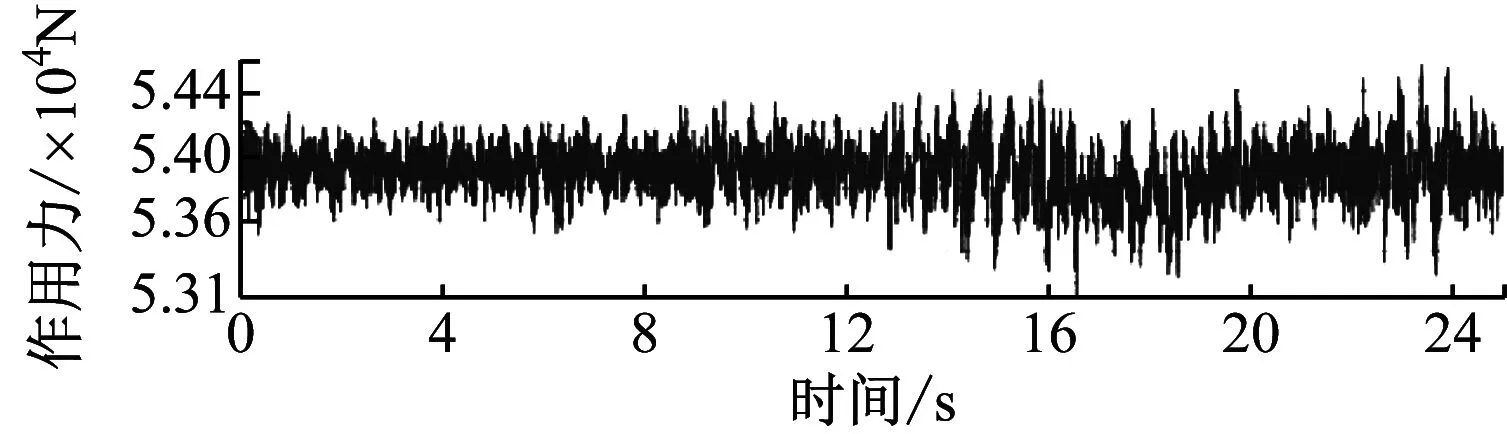
b) 右空气弹簧
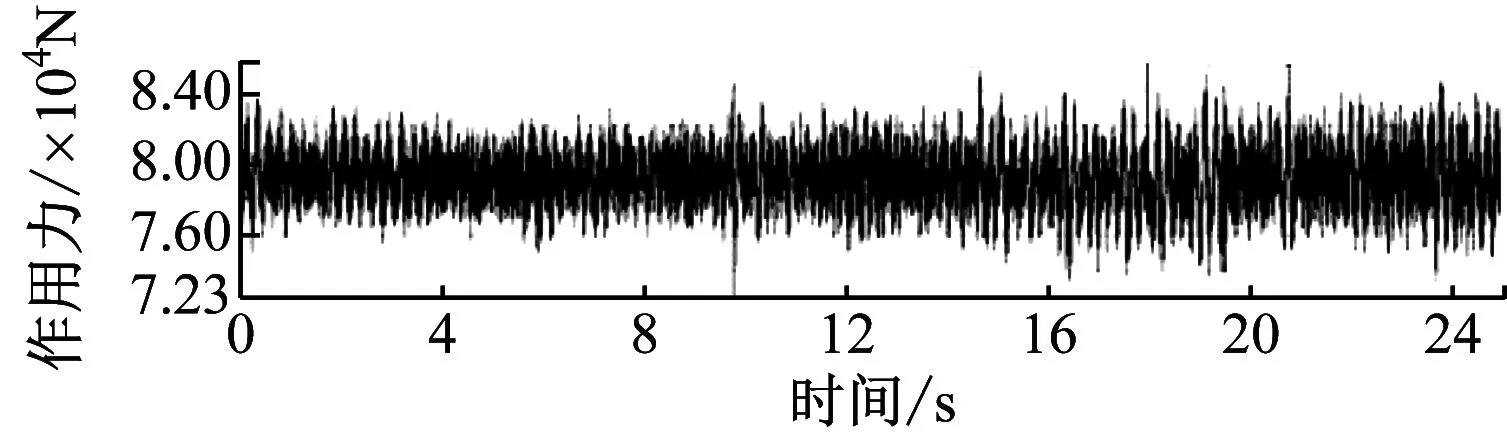
c) 前车轴
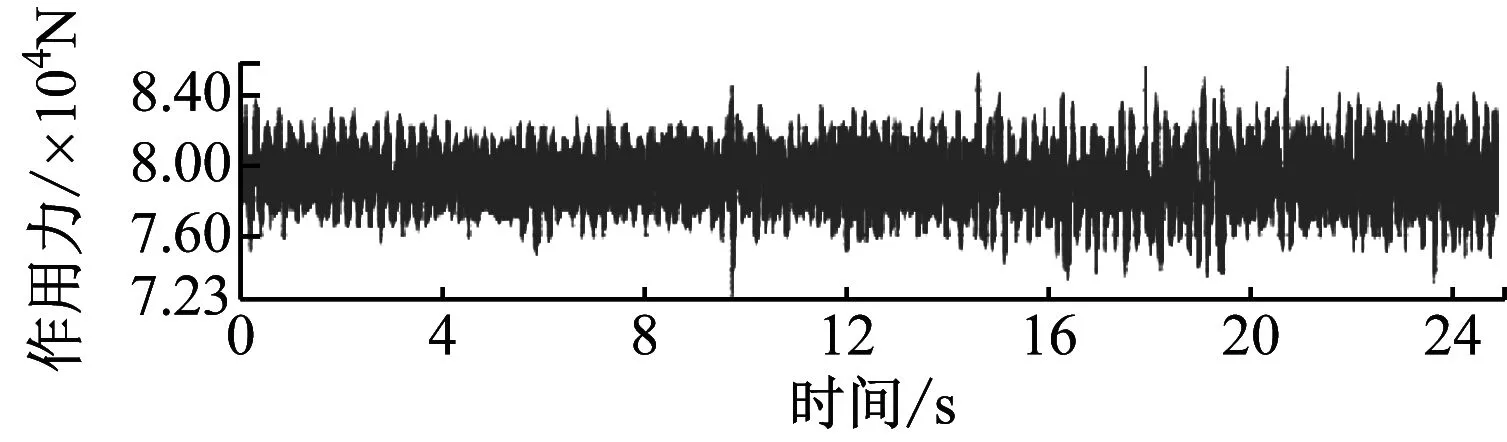
d) 后车轴
4 基于试验载荷疲劳寿命预测
4.1 平均寿命修正
跨坐式单轨车辆转向架构架所承受的主要载荷的应力循环特性是非对称循环,所以应考虑平均应力的影响。Goodman直线模型适用于脆性材料,对延性材料偏于保守,故选择Goodman直线平均应力修正方法。修正公式如下:
(4)
式中:
Sa——应力幅;
SN——修正之后的等效应力幅;
Sm——平均应力;
Su——拉伸极限强度。
4.2 S-N曲线
疲劳曲线在其有限寿命范围内的曲线方程为:
σmN=C
(5)
式中:
σ——疲劳极限;
N——疲劳试验循环次数;
C、m——材料常数,由疲劳试验确定。
查机械疲劳与可靠性设计可得,材料Q 345D的抗拉强度σb为490 MPa,应力比为-1、应力集中系数为1时,材料在N=103处的条件疲劳极限取为抗拉强度的0.9倍[4],疲劳极限的均值σ-1,103为441 MPa,材料在N=107处的条件疲劳极限取为抗拉强度的0.47倍[5],疲劳极限的均值σ-1,107为230.3 MPa。
为得到转向架构架材料实际的S-N曲线,需要对材料S-N曲线进行修正,标准光滑试样和构件的疲劳强度满足[6]:
(6)
式中:
σ-1c——构件的疲劳强度;
σ-1——标准光滑试件的疲劳强度;
βq——强化系数;
Kσc——综合修正系数,由式(7)确定。
(7)
式中:
Kσ——有效应力集中系数;
εσ——尺寸系数;
β——表面系数。
4.3 Miner法则
Miner线性累积损伤理论是工程上广泛采用的一种疲劳寿命计算方法。文献[7]详细介绍了线性、非线性、两级线性疲劳累积损伤理论。
记各应力水平下的寿命分别为N1,N2,…,Nr,各应力水平下的循环分别为n1,n2,…,nr,可得出:
(8)
式中:
ni——某应力水平下的循环数;
Ni——该应力水平下发生破坏时的寿命。
当损伤等于1时,构件发生破坏,即:
(9)
4.4 基于仿真载荷时间历程的疲劳寿命分析
将有限元模型导入Ncode软件中,读入各单位载荷工况下的应力分析结果,采用Goodman应力修正方法,设置存活率为99%,结合材料Q 345 D的疲劳特性曲线,将单位载荷工况下的应力结果与对应的载荷时间历程相关联,对构架进行全寿命疲劳仿真计算。
从仿真计算结果可以得出:疲劳寿命最短的节点对应的部位在转向架构架齿轮箱座下面的加强筋上,可经受的循环次数为2.588×107次,换算成可以安全行驶的里程数为1 080.49万km,大于转向架要求的安全行驶的里程数578.16万km(按时速33 km/h,每天工作16 h,每年运行365 d,设计寿命30年计算),寿命年数为56.1年。
4.5 基于试验载荷时间历程的疲劳寿命分析
从构架试验载荷疲劳寿命分析可以得出:疲劳寿命最短的节点对应的部位在转向架构架齿轮箱座根部,可经受的循环次数为2.861×107次,换算成可以安全行驶的里程数为1 194.5万km,大于转向架要求的安全行驶的里程数578.16万km,寿命年数为62.0年。
4.6 疲劳计算结果对比分析
由构架疲劳计算结果发现基于试验载荷时间历程激励的疲劳寿命比基于仿真载荷时间历程激励的疲劳寿命多了6年。对两种形式载荷历程的峰值、均值和频谱进行对比,结果如表1和图6所示。

表1 载荷谱峰值和均值对比分析表 N
由表1和图6可见,两种形式的载荷谱的主频都是2 Hz,但试验载荷谱的载荷幅值的峰值和均值都小于仿真载荷谱的峰值和均值,由此造成基于试验载荷的疲劳寿命高于基于仿真载荷的疲劳寿命。
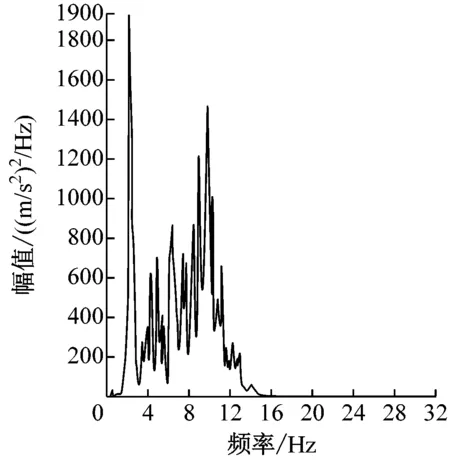
a) 仿真载荷谱频谱图
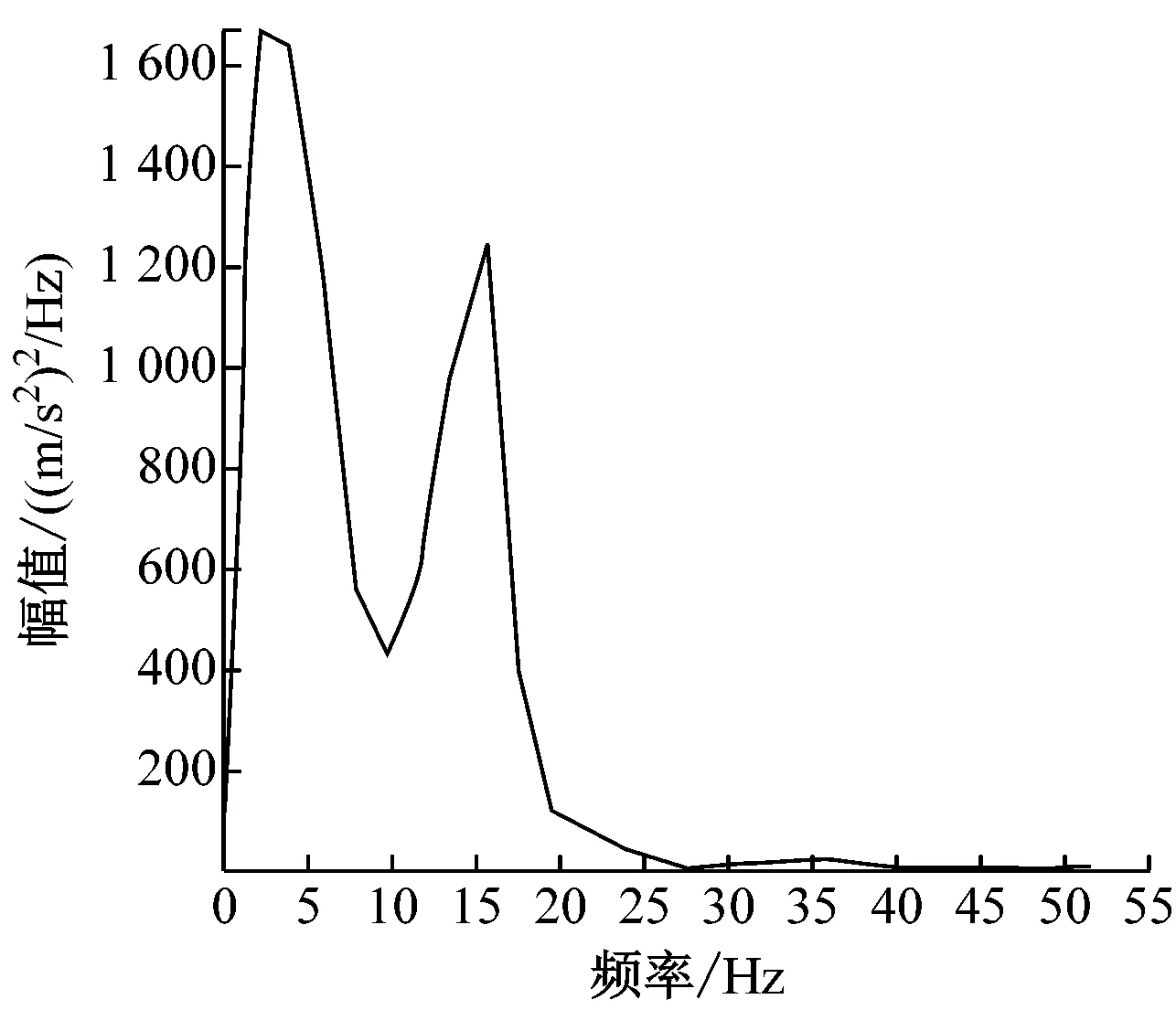
b) 试验载荷谱频谱图
5 结语
1) 基于仿真载荷的疲劳寿命小于基于试验载荷的疲劳寿命,说明基于仿真进行疲劳寿命预测具有可行性。
2) 为得到更准确的疲劳寿命,应对动力学仿真分析中的A级路面道路谱进行重新构造,以逼近跨坐式单轨走行面道路谱,提高仿真分析的准确性。
