搏动式电磁血泵电控系统的研究
2019-08-21陆通葛斌刘京京张少伟伍进平张宸
陆通 葛斌 刘京京 张少伟 伍进平 张宸
急性呼吸窘迫综合征(Acute respiratory distress syndrome,ARDS)是临床上比较常见的呼吸衰竭危急重症,表现为顽固性低氧血症、进行性加重的呼吸困难和呼吸窘迫,病人死亡率高[1−2].体外膜肺氧合(Extracorporeal membrane oxygenation,ECMO)技术作为ARDS重要的体外循环辅助治疗方式,可以有效纠正低氧血糖症,同时避免呼吸机相关性肺损伤[3−4].
ECMO包括泵血装置和氧合装置.目前ECMO使用的血泵有滚压泵和离心泵,滚压泵可提供搏动的血流,但由于其产生的压力极高,造成了较高的溶血性;而离心泵[5−6]具有对血液破坏相对较小,安全性高等特点,但在其使用过程中又有其维护价格昂贵、对人员操作技术要求高等问题;由于尺寸、能耗和稳定性以及可植入方面的优势,轴流式血泵[7−8]目前成为国内外研究的热点.由于以上血泵只能实现血液的一端进一端出,而不能模拟心脏左右两房室泵血;驱动方式均为电磁力矩的旋转驱动,流场会产生非生理性的流动及对血细胞的剪切应力[9],因此研究倾向于左心室辅助装置方向.
本文所设计的血泵基于磁体–线圈结构,通过理论计算与实验得到该结构应产生的动力大小,并由此确定工作电流大小;根据输出电流的要求来计算和设计控制电路,并提出一种用于搏动式电磁血泵的电控系统.利用控制电路、加速度传感器和示波器等搭建实验台,对空载状态下血泵的工作性能进行测试,验证该设计方案的可行性,为改进该血泵控制系统的方案和调整提供基础.本文的主要贡献和创新工作总结如下:
1)通过力学分析计算与实验,得到不同参数下磁体–线圈结构磁力与两者距离的关系曲线以及各因素对磁力影响的显著性,并利用分析结果确定血泵的基本工作参数.
2)根据血泵工作基本参数确定控制电路的输出电流值,并设计控制电路.
3)通过一系列实验得到血泵工作时间与加速度波形参数,利用上述参数设计程序验证血泵工作的稳定性与连续性.
1 搏动式血泵驱动的描述
1.1 血泵原理
本文所设计的搏动式电磁血泵由类似于心脏房室的血泵腔体、用于搏动的磁体以及为磁体运动提供磁场的线圈组组成,各线圈依次紧密排列;腔体被磁体分割成两个独立空间(类似于心脏的左右房室);磁体位于腔体内,当磁体磁场方向与线圈磁场方向相同时磁体将受吸力,而静止磁体的两极在磁场中受力不平衡时,磁体将沿着合外力方向运动.此血泵即利用磁体往复运动挤压腔体内的血液实现泵血的功能.原理图如图1所示,图中1为出入血口;2为线圈;3为磁体;4为泵体.
1.2 力学模型建立
对于计算磁体–线圈模型之间的磁力,国内一般采用有限元法得到[10];对于外文文献[11−12],Robertson等总结的方法主要包括:“Filament method(线等效法)”、“Shell method(面等效法)”以及“Integral method(积分法)”等方法.由于本文是磁体与线圈之间的作用力,而对于沿轴向磁化均匀的圆柱形磁体,可等效为相同体积的薄线圈,因此利用“Filament method”的方法,可将磁体和线圈等效为同形状无限薄的环电流.对于磁体的等效电流[12]如式(1);对于线圈的电流I2由稳压电源决定,因此磁体–线圈模型可以等效为双线圈结构.
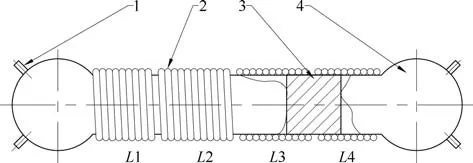
图1 血泵工作原理图Fig.1 Working principle of blood pump

2 血泵驱动的力学设计
2.1 磁力理论与推导
磁力可以由载流线圈之间的互感系数求得[13],之间的关系如式(2):I1I2分别为永磁体等效电流和线圈载流,zQ为广义坐标,由于两等效线圈为同轴位置,所以只需考虑力的轴向分量[14].

根据图2的两等效线圈,其互感方程如式(3)所示[13−14].
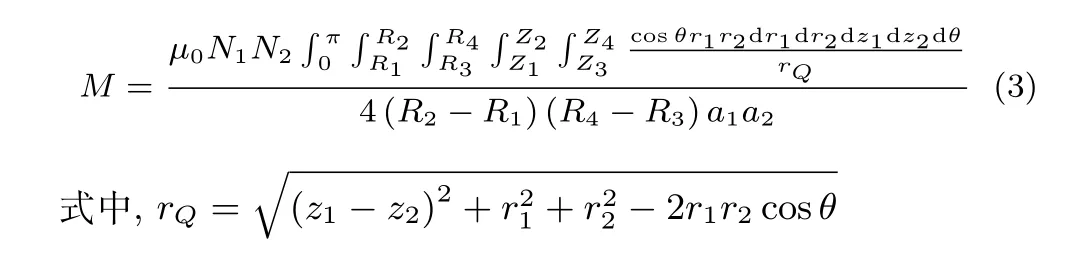
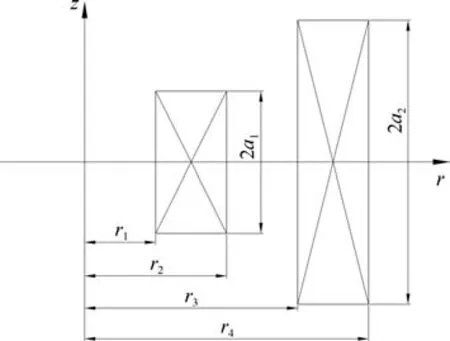
图2 双线圈模型Fig.2 Twin-solenoids model
此时的磁力:
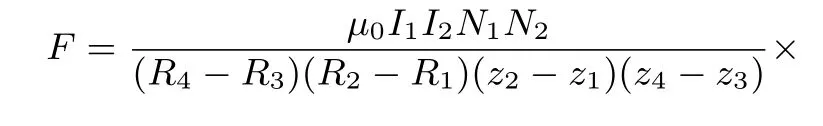

2.2 磁力正交实验
为设定血泵各参数的值,将各因素实验水平的顺序进行随机处理,如下表并进行正交实验.
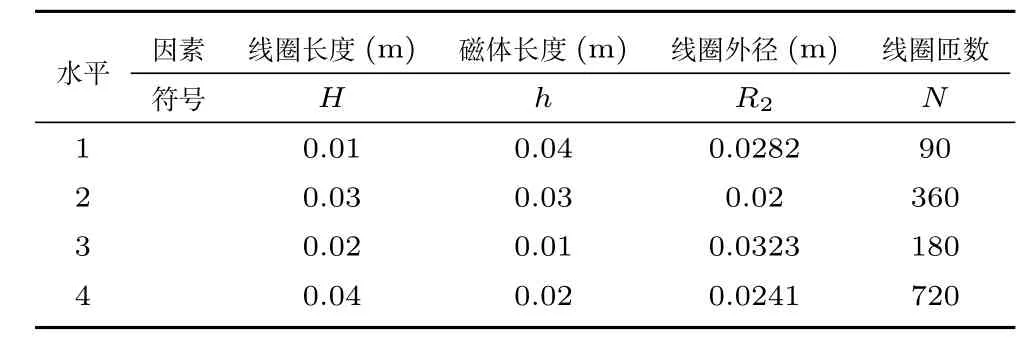
表1 磁力实验的因素水平Table 1 Levels of magnetic test factors
正交表L16(45)设计如下:
根据正交实验的结果,绘制磁力随各因素变化的趋势图如图3.
利用SPSS软件进行正交实验结果的方差分析如表3,由表1可以看出显著性顺序由大到小依次为:线圈匝数、线圈长度、磁体长度、线圈外径.
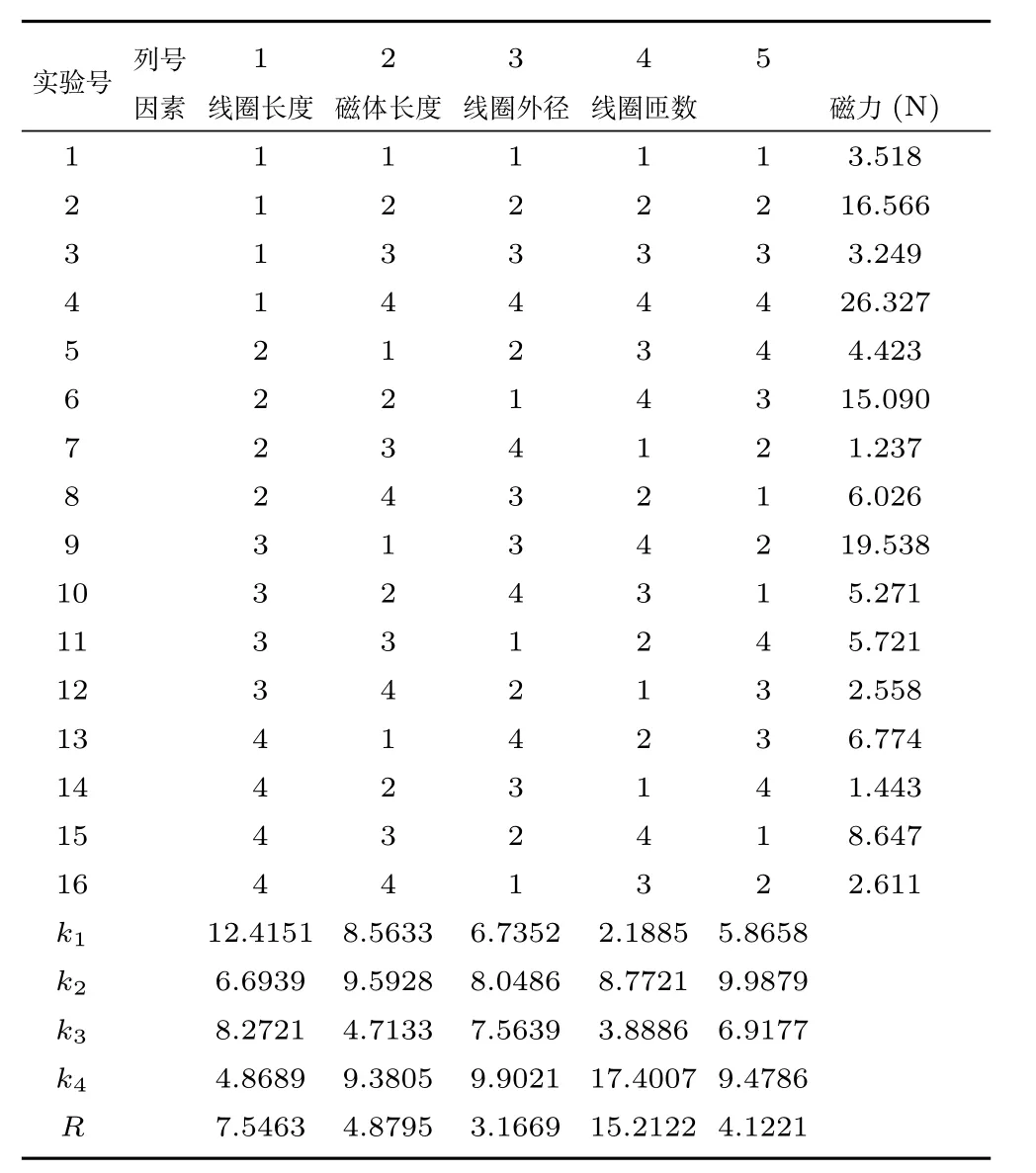
表2 磁力实验结果及极差分析Table 2 Magnetic test result and range analysis
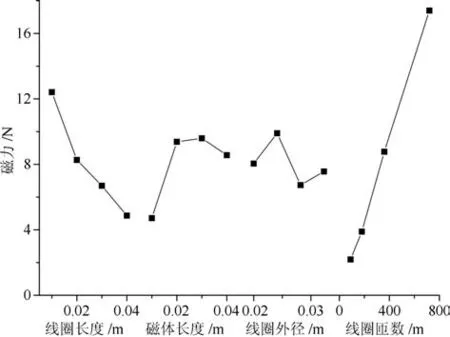
图3 磁力随各因素变化的趋势图Fig.3 Line chart of magnetic force variation with various factors
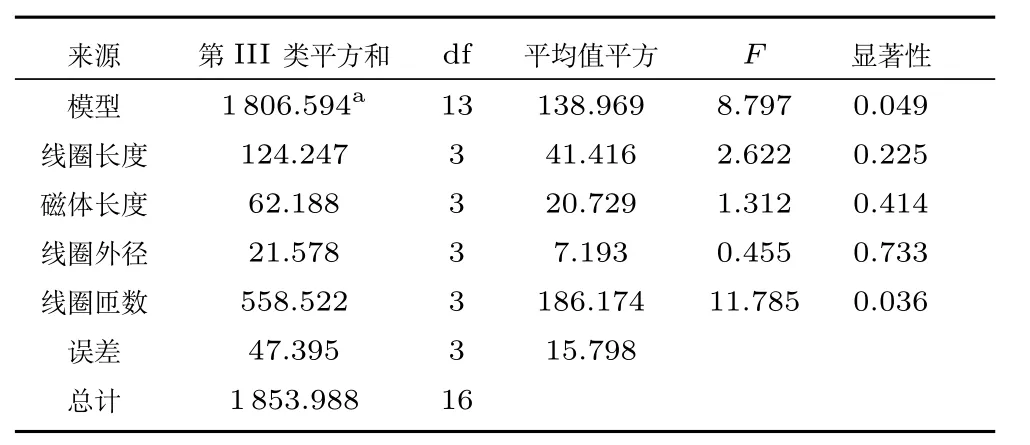
表3 正交实验结果方差分析Table 3 Variance analysis of orthogonal test
2.3 力学分析
根据显著性分析结果,选取永磁体为圆柱形N35的烧结钕铁硼磁铁,直径φ35mm,厚度h=2a2=20mm;线圈宽度为LN2=20mm,线圈厚度为2层,漆包线厚度为φ0.41mm,作为薄壁螺线管处理R3=R4,正常成年人[10]平均动脉压正常值为70∼105mmHg,则计算产生此压强的血压需F0=1.13N.根据国家标准,体外循环设备主动脉供血时使用管路内径为3/8in,即9.525mm,因此血液阻力F1=0.097N,而磁体的摩擦系数µ约为0.01∼0.001,取摩擦力F2=0.02N.为满足安全需求,取安全系数为2并取整,得到F1=0.2N,F2=0.05N,则所需平均驱动力F=F0+F1+F2=1.383N.利用Mathematica绘制不同电流下磁力随距离变化的图像如下图所示.
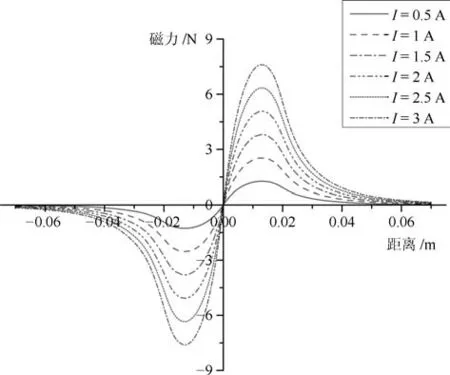
图4 磁力–距离关系图Fig.4 The relationship between magnetic force and distance
当线圈与磁体的距离为zQ=0.02m,即线圈与磁体刚好接触时,利用式(6)计算磁体与线圈之间的磁力,磁体受力理论值与磁体所受力实际值及摩擦力如表4和表5所示.载流线圈各匝的磁通总和为称为磁链Ψ,理论上若N匝线圈的磁通均为Φ,则磁链Ψ=NΦ.然而各交链的磁通不一定完全相同[17],因而影响磁链Ψ值;同时线圈通电产生的热量,磁体本身的表面处理等都会对作用力产生影响.利用测力计和血泵实验平台测量实际值:首先用测力计测得泵体固定时,磁体在缓慢滑动的情况下摩擦力的大小.设定磁体在线圈L1处于受力平衡的位置,为磁体向线圈L2运动的初始位置.线圈L2通电待磁体稳定后,用测力计测其初始位置时拉力大小.

表4 当zQ=0.02m时不同电流产生的磁力Table 4 Different magnetic force caused by different current when zQ=0.02m
从图3可以看出,磁体与线圈之间的磁力与线圈电流大小以及两者之间的距离有明显关系,当两者距离从0开始逐渐增大,磁力先增大后减小.在磁力增大过程中,增长率随距离的增大而减小;在减小过程中,衰减率随距离的增大先增大后减小.
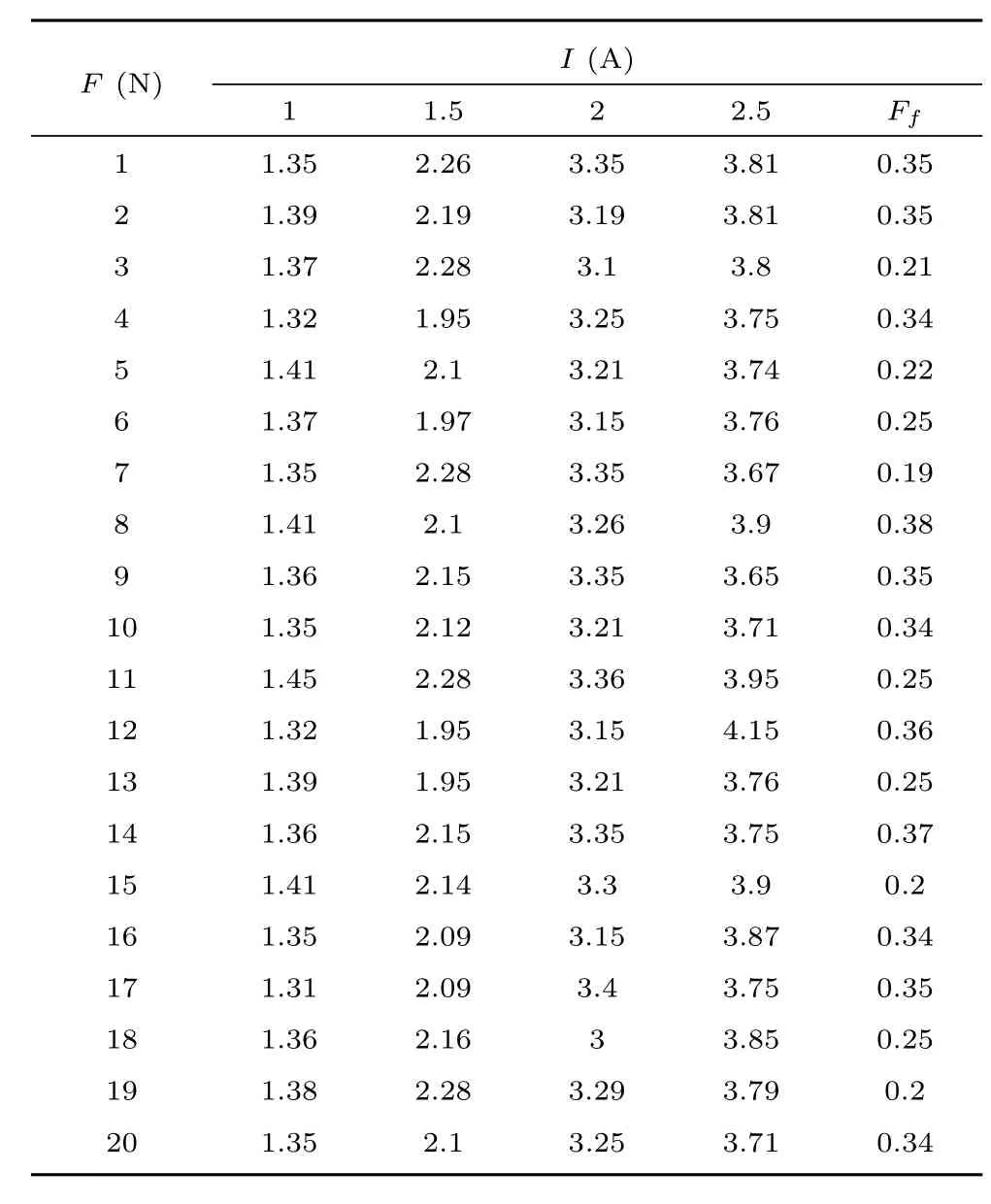
表5 在不同电流下实际测得磁力及磁体所受摩擦力Table 5 Different magnetic force caused by different current and the friction on permanent magnet slider
结合上图的趋势从表4可知,当电流I≤0.5A时,计算所得线圈与磁体在设定位置力不大于0.93N,因而小于血泵正常工作所需要的力;而当I≥3A时,计算所得的磁力将超过5.56N明显大于1.383N超过工作需求.
从表5可知,实验测得磁体所受磁力略小于理论计算值,磁体在腔体内的摩擦力略小于电流为0.5A时的理论值,因此选1.5A电流可保证血泵工作充足的动力性.
3 血泵驱动的电学设计
3.1 控制电路理论设计
搏动式电磁血泵驱动系统电路框图如图5.系统通过单片机将信号经转换电路将数字信号转换为模拟信号,经同相比例运算电路和达林顿管组成的放大电路向线圈输出,由继电器控制线圈的工作顺序实现泵血的功能.
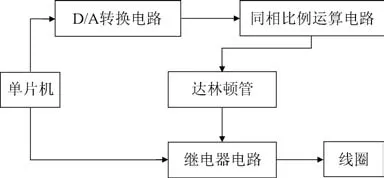
图5 实验原理图Fig.5 Schematic diagram of experiment
控制电路如图A1所示,电路采用单片机(U1)为AT89C52[18],D/A(U2)转换采用 DAC0832芯片[19−20],此八位芯片可根据需要输出0x00∼0xFF的不同大小电流.单片机P0口作为通用I/O口与DAC0832芯片的输入端DI0∼DI7相连,采用直通方式,通过运算放大器[21]LM324(U3A)输出电压信号.
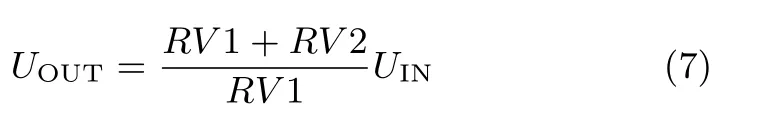
D/A转换后串联同相比例运算电路[18]和达林顿管TIP142[22](同相比例运算电路由U3B,可调电阻RV1,RV2组成,RRV1=10kΩ,RRV2=20kΩ)的局部电路如图A2.由式(7)可得同相比例运算电路放大的比例为3倍,即电压输出UOUT=15V.由于达林顿管由两个三极管串联得到,因此可以估算其输出电流:在理想状态下,VBB=UOUT=15V,VCC=15V,VBE=1.4V,可以求的VEE=13.6V,根据式(8)可以估算出状态下的电流大小为IE=3.16A.

使用继电器[23](RL1,RL2)控制血泵电磁线圈(L1∼L4)的通电顺序,继电器为低电平触发,由单片机通过经P2.6,P2.7口控制.血泵的继电器分为两组,线圈L4、L2分别接继电器常闭和常开触点,为第一组;线圈L1、L3分别接继电器常闭和常开触点,为第二组,运用Proteus软件绘制电路图并仿真得到输出电流的大小.
3.2 控制原理
单片机发出的信号控制继电器触点切换实现工作线圈的切换,由于在泵血时需要保证对血液应产生足够的压力,即要求泵体内部的磁体保持运动的连续及相对恒定的加速度,因此血泵空载时磁体需做加速运动,磁体经过各个线圈的时间各不相同.
在单片机控制系统中程序由C语言编写,主要包括主程序和定时器程序.
主函数用于:1)完成各种设置(如设置堆栈和单片机初始化等工作);2)通过定时器程序控制继电器[23]触点开闭工作的时间间隔以切换线圈组及控制线圈的工作时间;3)通过向D/A[19−20]转换器输出的数字量以控制该系统的输出值.
定时器函数主要用于设置定时时间,主函数通过循环运行若干次定时器函数实现对电路中元件运行时间的控制.由于磁体在运动过程中做加速运动,因此定时器控制时间的参数需经过实验获得.
4 电控实验
血泵实验平台包括控制电路部分、泵体部分和测试部分.控制电路部分和泵体部分如上文所述,测试部分包括加速度传感器和示波器等.本实验用于获取泵体部分的工作参数,包括血泵线圈的电阻值、磁体在磁场中运动状态与加速度波形的关系.
4.1 线圈的参数实验与仿真
取电源的输出电流为0.5∼3A,间隔0.1A分别向各个线圈通电20次,读取电压值并求得平均数,各线圈电压结果如表6.利用欧姆定律求的各线圈阻值的平均数分别为:RL1=2.2Ω;RL2=2.1Ω;RL3=2.0Ω;RL4=2.1Ω.
根据线圈的电阻参数设置Proteus软件电路图的阻值,设置同相比例运算电路的可调电阻RRV1=10kΩ,RRV2=20kΩ.运行Proteus仿真电路,仿真显示线圈通过的最大电流为3.12A,明显大于1.5A满足磁力计算的电流值.
4.2 磁体的加速度波形实验
连接设备如图A3,取工作电流为1.5A以保证磁力.当磁体处于初始位置,将线圈L2接入稳压电源,示波器A,B端口分别接加速度传感器和线圈,此时磁体运动受力而产生的加速度状态可由加速度传感器输出反映.示波器横轴为时间轴,磁体运动加速度波形的持续时间由横轴读取;纵轴为电压轴,示波器加速度电压输出信号.根据图6(a)示波器显示,图中图线1为加速度波形,图线2为参考电压;第一段正向波段即为磁体单向运动时间,从图中可以读出磁体起始加速时间约为0.1s.由此编写程序:设置通电时间为0.1s,间隔时间为10s,启动单片机后预留10s准备时间.工作0.1s断电后,磁体做减速运动直到速度减为0.过程中,磁体从线圈L1的位置运动到线圈L3的位置.图6(b)正向波形为加速持续时间0.1s信号,负向波形为减速波形.
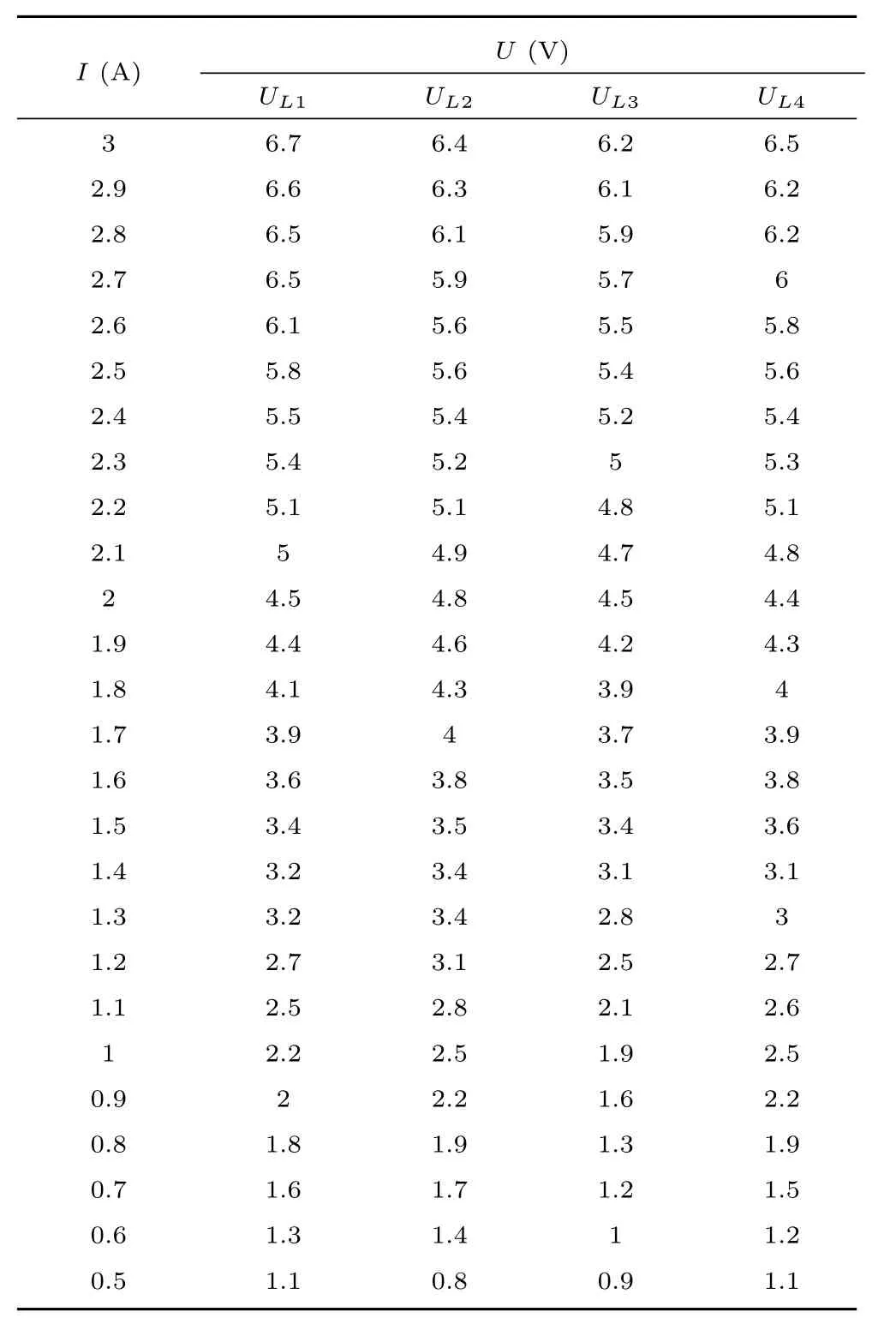
表6 血泵线圈通过电流与电压关系Table 6 The relationship between current and voltage of blood pump coils
4.3 血泵连续工作实验
本实验利用稳压电源、单片机电路、加速度传感器和示波器,确定磁体运动单向连续性的相关参数并验证.继电器对线圈的控制电路图如图A3.在泵血过程中,磁体从起始位置由电磁线圈驱动依次经过线圈L2、L3与线圈L4重合,随后再回到起点位置即一个运动周期.实验在1.5A电流的作用下获得磁体连续运动的控制参数,并以此为依据编写单片机驱动程序,实现磁体的连续运动.为确保运动的连续性,设计线圈前半周期的通电顺序为线圈L1、L4,线圈L2、L3,线圈L3、L4,线圈L1、L4.
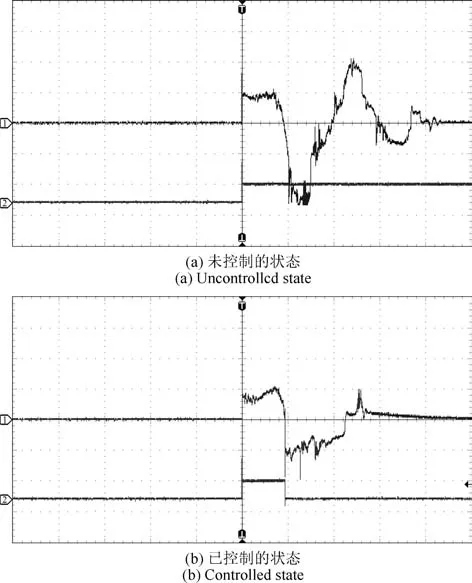
图6 示波器所观察到的信号和观察到持续0.1s的信号Fig.6 Output of acceleration waveform and output of 0.1s sustained signal observed by oscilloscope
首先对线圈L1、L4通电,使其处于工作的初始位置.设置线圈L2和L3工作时间为1s,运用上一实验方法确定其单向加速过程的时间.由输出波形可知磁体在本段单向运动时间为0.1s,编写程序设置单片机控制线圈L2、L3工作时长的应为0.1s.在测其单向加速过程的时间时,为保证磁体运动不受线圈L4的影响需首先把继电器RL1的常闭触点与继电器RL2的公共端直接连接,断开线圈L4.
确定线圈L3、L4的工作时长应保证磁体具有的磁体经过线圈L2、L3后的初速度,即磁体从初始位置运动到其在线圈L2、L3受力平衡位置时,线圈L3、L4通电L2断电.设定L2、L3的通电时间为0.1s;设定L3、L4的通电时间为2s.磁体自初始位置起,单片机向线圈L2、L3通电0.1s使磁体到达线圈L2、L3所产生磁场的受力平衡位置;随后向线圈L3、L4通电,磁体经过0.03s到达线圈L3、L4所产生磁场的受力平衡位置.从输出波形的时间轴读取磁体在此段运动时间为0.03s,则单片机控制L3、L4工作时长为0.03s.
同理设定L2、L3的通电时间为0.1s;L3、L4的通电时间为0.03s;L1、L4通电时间为2s.从输出波形的时间轴读取磁体在此段运动时间为0.01s,则单片机控制L1、L4工作时长为0.01s.
本实验通过示波器输出的加速度波形如图7所示,按照图中顺序,分别为磁体从初始位置运动到线圈L2、L3,线圈L3、L4,线圈L4以及前半周期的波形.磁体在前半周期的运动时间为0.14s,因此整个周期各组线圈的工作时长如表7所示.

表7 血泵线圈工作时长Table 7 The working time of blood pump coils
当单片机晶振为12MHz,采用定时器方式2,则函数每循环4000次计时1s,由以上实验获得的参数编写程序即可实现磁体的连续运动即血泵的稳定工作.
5 结论
论文从理论和实验的角度出发,设计了适用于驱动搏动式电磁血泵工作的电控系统模型.通过理论计算分析了磁力与磁体之间距离以及影响磁力的因素;通过实验测得当线圈负载为1.5A时,磁体在初始位置的平均作用力可以满足血泵动力需求.血泵泵体部分为缠绕了4组线圈的塑料管,结构设计的4组线圈参数相同,因此在相同阻力的条件下各线圈对磁体的作用力相等.
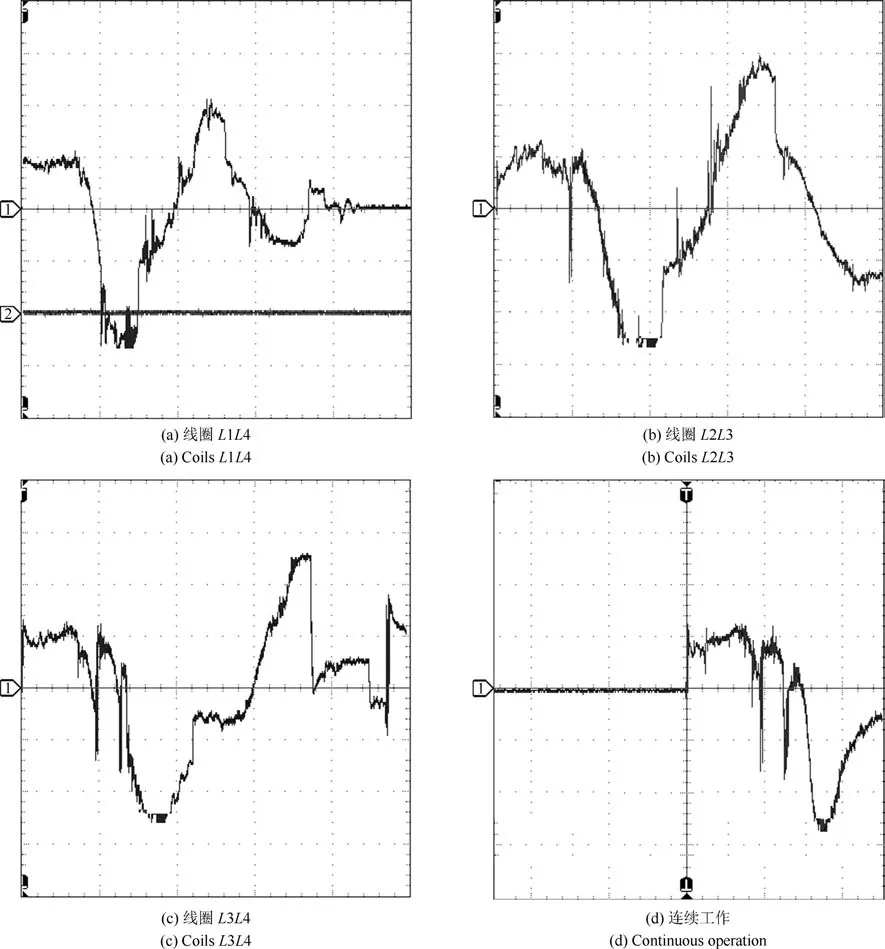
图7 示波器所观察到的信号Fig.7 Output of signal observed by oscilloscope
本文利用Proteus软件设计并仿真了控制电路,根据线圈的电阻实际测得最大输出3.1A.该电路可根据需要输出256种不同大小的电流,实现电流输出的变化;同时可以通过调节同相比例运算电路两可调电阻的阻值来对输出电流值进行微调.通过磁体的加速度波形实验,确定了磁体各运动状态与加速度变化的关系及磁体单向运动的控制方法;通过磁体运动的连续运动实验,得到了控制磁体在线圈中连续单向运动的有关参数.最后根据以上参数编写了程序,通过实验验证了磁体单向运动的连续性.
综上所述,本文测试表明设计的电控系统使血泵各参数满足搏动式磁力泵的动力需要,验证了该电控系统对血泵控制的稳定性和连续性达到了研究的目的.此研究对于进一步优化电磁驱动控制具有重要应用前景,尤其对于ECMO的发展和推广以及对于体外循环血泵的发展具有重要意义.
附录A
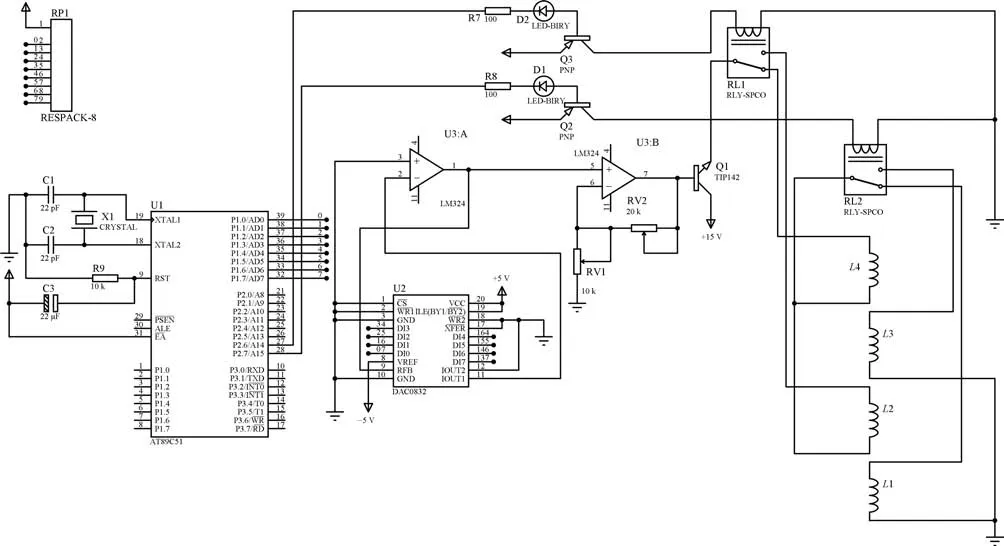
图A1 控制电路Fig.A1 Control circuit
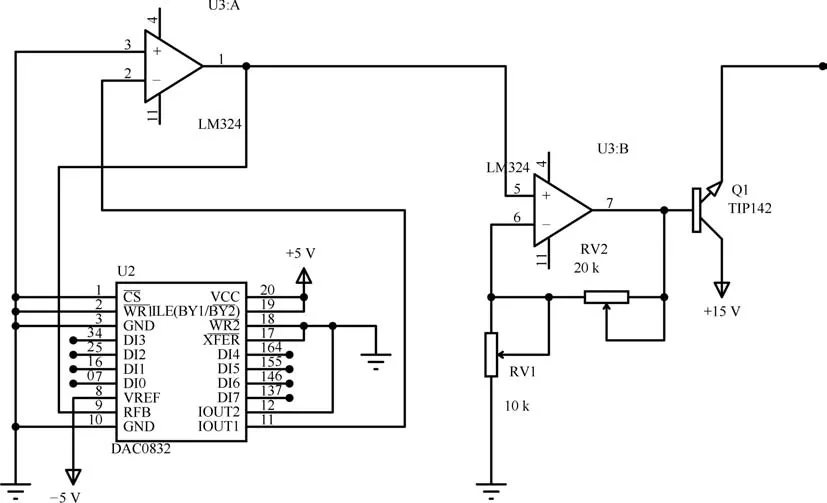
图A2 放大电路Fig.A2 Amplifying circuit
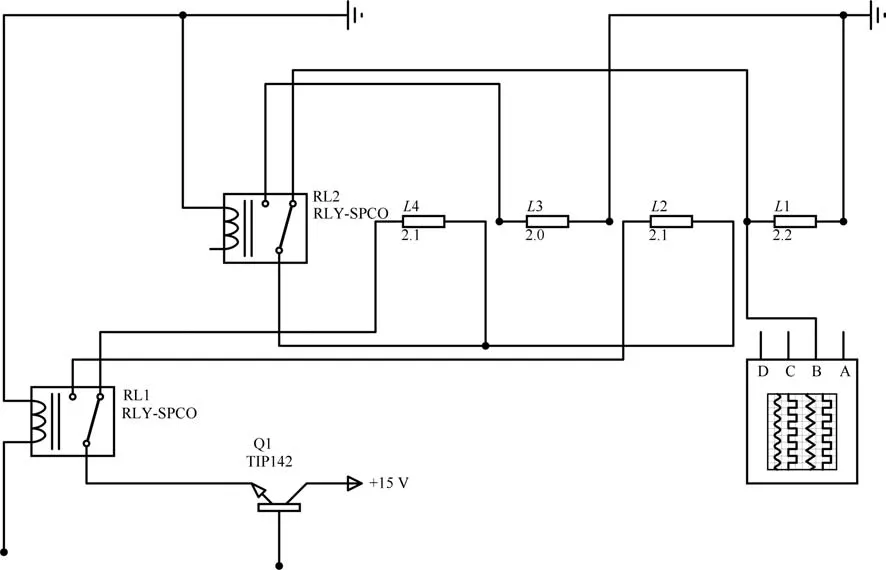
图A3 实验电路Fig.A3 Test circuit
