卫星星箭耦合力学分析模型二次缩聚方法

谢伟华，尹家聪，林勇文，董 锴，陈 曦，李正举

（1. 中国空间技术研究院 通信卫星事业部，北京 100094； 2. 北京宇航系统工程研究所，北京 100076）

0 引言

建立卫星有限元物理模型并进行力学分析是卫星结构分系统设计、组件力学试验条件制定、正弦振动力学试验预示以及星箭耦合分析的重要基础。有限元缩聚技术是利用模态综合法[1-7]，将有限元物理模型内部节点的刚度、质量信息缩聚在边界点上，生成缩聚模型。采用有限元缩聚模型代替物理模型进行力学分析，一方面可以避免输出结构设计的技术细节，起到技术保密的作用；另一方面可以大大减少模型本身的自由度，有利于提高力学分析的计算效率。

模态综合法在航天器设计制造中应用广泛：运载火箭的建模[8-9]，星箭耦合分析[10]，大型部件如航天相机、氦气瓶等的建模[11-12]，复合柔性结构航天器建模[13]以及卫星的动力学分析[14]中均有采用此方法。

卫星发射任务中，卫星设计方须向运载设计方提供卫星有限元缩聚模型（主要包括缩聚后的刚度矩阵、质量矩阵和星上特征点的响应转换矩阵）作为星箭耦合分析出口模型，与火箭模型进行主动段耦合载荷分析（coupled load analysis，又称“星箭耦合分析”），输出星箭界面冲击谱及星上特征点的响应。星箭界面冲击谱是整星正弦振动试验下凹条件制定的重要依据；特征点响应可用于评估星上部件在主动段飞行过程中的响应水平，以及星外大部件与火箭整流罩的振动干涉情况。

目前，星箭耦合分析出口模型主要采用“一次缩聚技术”获得，即首先建立卫星整星的有限元物理模型（其中包括天线、太阳电池阵等大部件的纯物理模型，而非缩聚模型），然后利用固定模态综合法将整星有限元模型缩聚到星箭界面，生成星箭耦合分析出口模型。然而，随着卫星产业的不断发展，多部门甚至不同国家间的合作越来越多，卫星制造方有时无法获得大部件的纯物理模型，须利用已缩聚过的“一次缩聚模型”进行“二次缩聚”。为此，本文提出一种将包含天线缩聚模型的卫星有限元模型进行二次缩聚，输出星箭耦合分析出口模型的方法，并与火箭研制方联合开展星箭耦合分析及结果校验，以验证该方法的有效性。

1 二次缩聚方案

1.1 二次缩聚流程

1）在有限元软件中建立卫星主结构发射状态的有限元物理模型。

2）在有限元软件中建立卫星全部次级结构在发射收拢状态的有限元物理模型。

3）利用混合界面模态综合法，将需要一次缩聚的次级结构有限元物理模型分别缩聚到各自的一组固定界面边界点和自由界面边界点上，获得次级结构的一次缩聚数学模型。其中，固定界面边界点应设置为次级结构与卫星主结构的安装连接点，自由界面边界点应从次级结构的外轮廓点及外表面上振动响应最大的点中选取。

4）在有限元软件中，将卫星主结构的有限元物理模型依次和每个次级结构有限元物理模型或一次缩聚模型通过梁单元或多点约束单元模拟安装螺钉装配在一起，获得含一次缩聚次级结构的卫星有限元混合模型。当采用多点约束单元装配时，主节点应设置为各缩聚模型的固定界面边界点，从节点应设置为次级结构在卫星主结构上对应的安装点。

5）选择卫星有限元混合模型中各结构舱板及各次级结构的振动响应最大的节点构建星箭耦合载荷分析需要计算的内部响应点集合，从有限元软件中提取混合模型的刚度矩阵和质量矩阵，采用固定界面模态综合法将该有限元混合模型缩聚到卫星与运载火箭的界面节点上，获得二次缩聚后的刚度矩阵和质量矩阵，以及内部响应点对应的转换矩阵。

1.2 混合界面模态综合法原理

假设有m个次级结构的有限元模型需要进行一次缩聚，那么对每个次级结构i（i=1, 2, ···,m），从有限元软件中提取其在自由边界条件下的刚度矩阵K(i)和质量矩阵M(i)；选择次级结构i的个固定界面边界点和个自由界面边界点作为缩聚模型的保留节点，用个PLOTEL显示单元将保留节点连接起来，获得次级结构缩聚模型的显示轮廓。记固定和自由界面边界点对应的自由度集合分别为B(i)和C(i)，剩余的内部自由度集合为O(i)；并将K(i)、M(i)按 B(i)、C(i)、O(i)的自由度顺序重新排列为矩阵分块形式[7]：

式中：上标(i)及下标B、C、O表示第i个次级结构的刚度矩阵、质量矩阵中对应于 B(i)、C(i)、O(i)的行或列。确定次级结构i的缩聚模型需保留的广义自由度为q(i)，其值一般取为50～200，记其集合为Q(i)，并用Lanczos或其他特征值解法求解次级结构i的广义特征值问题

计算次级结构i一次缩聚后的刚度矩阵=(T(i))TK(i)T(i)和质量矩阵=(T(i))TM(i)T(i)，其中缩聚转换矩阵T(i)为

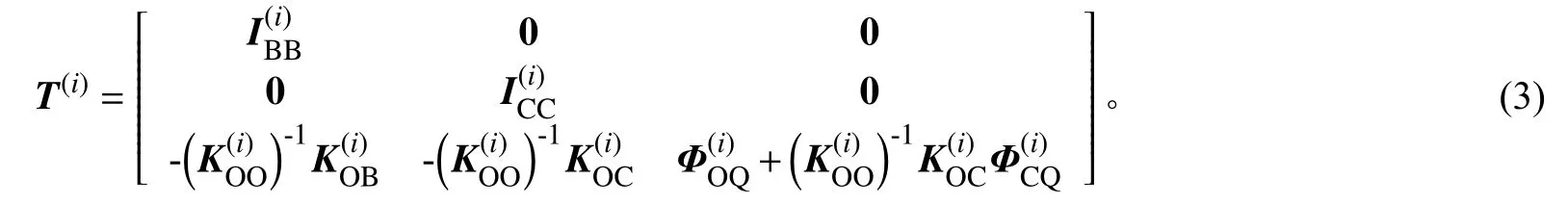
将次级结构i的一次缩聚模型整理为有限元软件可识别的数据文件，存储内容包括：

1.3 二次缩聚原理

选择卫星有限元混合模型中重点关心的各主结构舱板以及天线、太阳电池阵、气瓶、贮箱等次级结构上振动响应最大的点作为载荷耦合分析需要计算的内部响应点（其自由度集合记为U）。记卫星有限元混合模型与运载火箭的星箭界面主节点的自由度集合为B，其余自由度集合为O，提取卫星有限元混合模型在自由边界条件下的刚度矩阵K和质量矩阵M，并将它们按B、O的顺序排列为[2]：

用Lanczos或其他算法求解广义特征值问题

2 算例验证

2.1 一次缩聚

假设将某卫星的一副对地天线有限元模型进行一次缩聚，如图1所示，该有限元模型包含壳单元和体单元，节点数约2.5万，单元数约7万，自由度数约7.5万。利用1.2节的混合界面模态综合法，对有限元软件Nastran进行二次开发，可将天线的有限元物理模型（图1(a)）转化为有限元一次缩聚模型（图1(b)）。一次缩聚后的模型包含22个PLOTEL轮廓单元，仅有148个自由度（包括100个正交模态），相比物理模型的自由度减少了2个数量级。

图1 天线有限元模型Fig.1 The finite element model of antenna

表1给出了该天线缩聚前/后在固定边界条件下的固有频率对比结果，可以看出，该天线的有限元物理模型和缩聚模型的振型和固有频率一致。说明一次缩聚算法正确有效，可用于卫星整星的有限元建模。

表1 某天线有限元模型一次缩聚前/后的固有频率对比Table 1 Comparison of natural frequencies of an antenna between reduced and unreduced finite element model

2.2 二次缩聚

将该卫星另一副对地天线用相同方法进行一次缩聚得到有限元缩聚模型后，再将2副天线的有限元缩聚模型都装配到卫星的有限元模型上（如图2所示），并使用1.3节的二次缩聚方法对该混合模型进行二次缩聚。

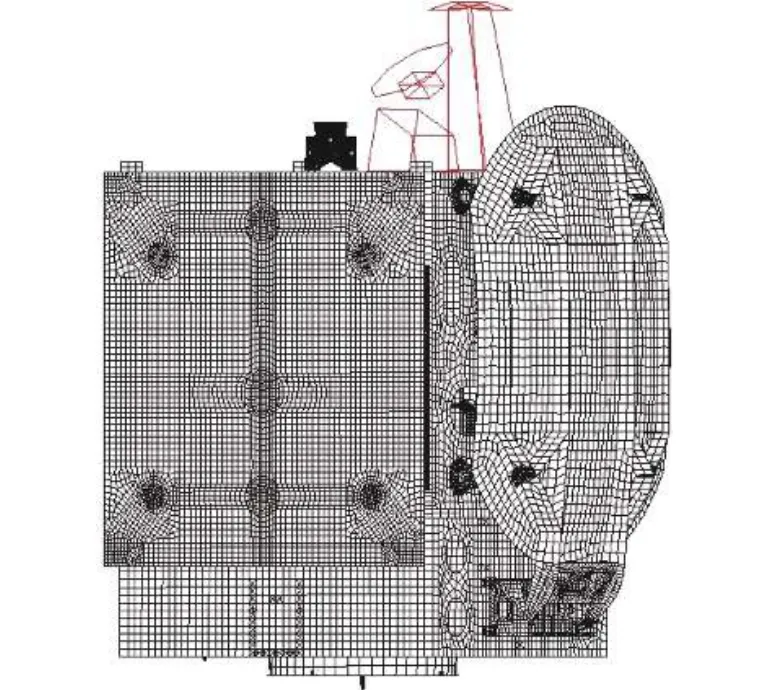
图2 天线有限元缩聚模型与整星装配图Fig.2 A finite element model of a satellite containing both unreduced and reduced sub-structures

2.3 二次缩聚结果验证

为了验证二次缩聚在星箭耦合分析中的正确性，将不包含任何缩聚模型的卫星整星有限元物理模型（如图3所示）采用现有的一次缩聚方法进行缩聚。

图3 天线有限元物理模型与整星装配图Fig.3 A finite element model of a satellite containing unreduced sub-structures

将由图2和图3分别生成的整星星箭耦合分析出口模型均提供给火箭研制方，联合开展星箭耦合分析及结果校验，得到某工况下星箭界面点x向等效正弦谱，如图4所示。可以看出，2种模型的结果曲线吻合很好，验证了本文所提出的二次缩聚方法的正确性。

图4 某工况下星箭界面x向等效正弦谱对比Fig.4 Comparison of coupled load analysis results between one-time and second-time condensation models

3 结束语

本文以大型复杂航天器为对象，研究了利用混合界面模态综合法进行一次缩聚的原理，以及将该一次缩聚模型装配于星本体物理模型上进行二次缩聚的方法；给出算例验证基于混合界面模态综合法的一次缩聚及二次缩聚方法的正确性，并进一步与火箭研制方合作开展星箭耦合分析验证该方法的正确性。结果表明：利用混合界面模态综合法进行一次缩聚的天线有限元模型规模大幅下降，且基频、振型等与有限元物理模型一致；利用二次缩聚方法将含天线一次缩聚模型的整星模型进行二次缩聚后，与原有一次缩聚法生成的星箭耦合分析出口模型的x向等效正弦谱一致，即本文的二次缩聚方法可以用于将含子结构一次缩聚模型的卫星有限元混合模型进行二次缩聚。

本文的一次缩聚方法可用于将卫星上的部件进行一次缩聚后装配于整星上进行动力学分析，可大大减少分析计算量，提高计算效率；二次缩聚方法解决了含一次缩聚模型的航天器有限元混合模型的再次缩聚问题。以上方法可以扩展到其他行业如航空、船舶等的动力学分析中。