基于ArcGIS Runtime模型三维姿态旋转变换的研究

(成都理工大学 四川 成都 610059)

引言

ArcGIS Runtime 是ESRI公司开发的二次开发包，可构建本地应用程序并将其部署到各种流行的平台和设备中。为原生应用添加强大的空间功能，并使应用用户能够执行所有GIS。三维坐标转换一直是测量领域的一个重要内容[1]，在图形学中，三维建模技术提供了很多必要的方法用来将现实世界中的物体转化为三维坐标系下的数学表达形式,并通过计算机程序进行渲染,从而实现在虚拟空间中模拟真实世界的效果[2]。三维坐标转换中最重要是坐标转换参数的求解。坐标转换参数分为旋转、平移和尺度参数，其中旋转参数的确定是坐标转换的核心[3]。本文将通过控制变量的方法进行观察ArcGIS Runtime的旋转现象，并通过该现象推导出ArcGIS Runtime的旋转机制，计算出该旋转机制的旋转矩阵，然后进行不同旋转机制旋转角的解算，最后验证成果。

一、三维模型旋转机制的确定

本文实例三维模型为电塔模型，该模型是由多个组件模型通过三维空间旋转角和坐标定位定姿态组合而来，旋转角及坐标都存储在renderALL.db数据库中，该模型的旋转机制如下：

1.绕Heading轴旋转Rotate_z，用于确定模型侧身角度。

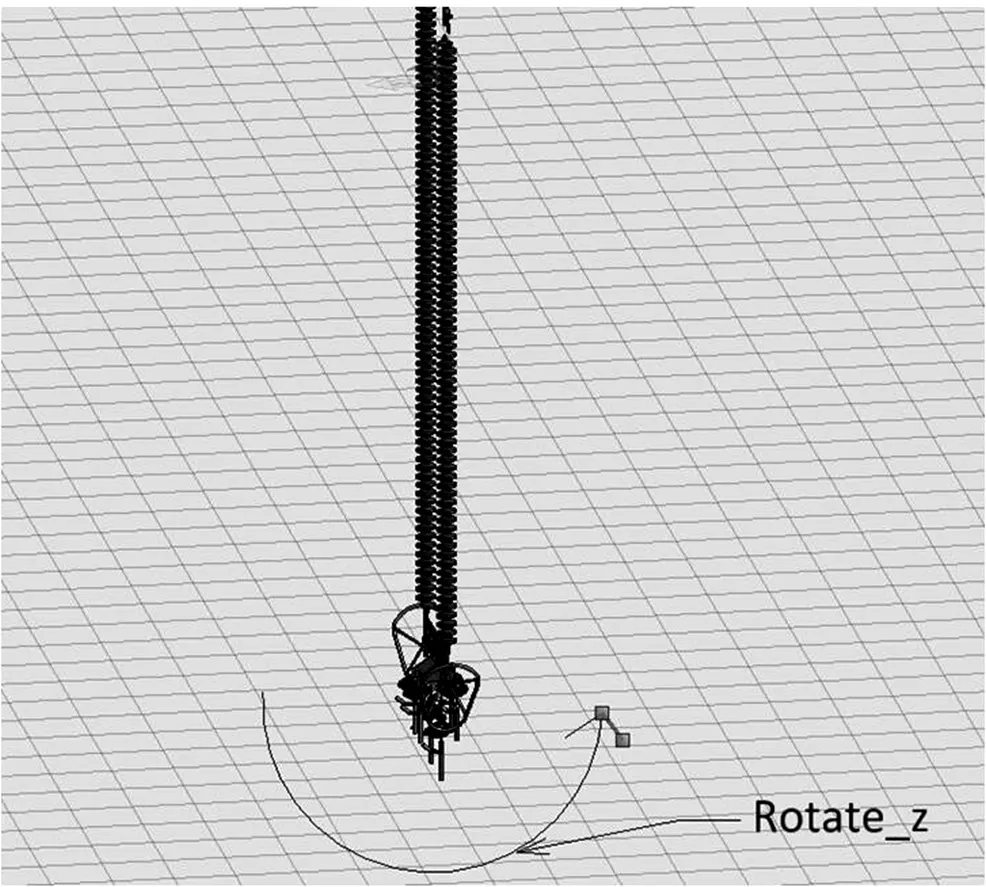
图1 绕Heading轴旋转Rotate_z

2.绕Roll轴旋转Rotate_x，用于确定模型俯仰角度。

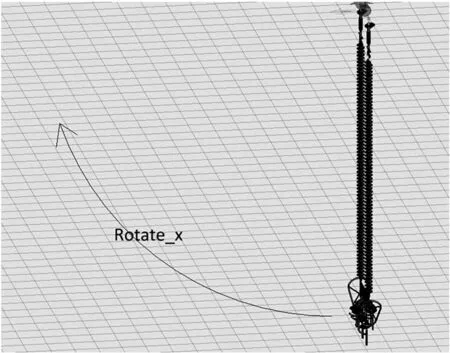
图2 绕Roll轴旋转Rotate_x

3.绕Heading轴旋转Rotate_y，第二次绕Heading轴旋转弧度值，用于确定模型的指向方向。

图3 绕Heading轴旋转Rotate_y

4.从以上描述可以看出该模型的旋转机制是Heading-Roll-Heading的不带轴旋转。

二、ArcGIS Runtime三维姿态旋转机制的确定

(一)技术路线

图4 技术路线

首先通过对模型的转动进行其转动轴方向的确定，然后对是否带动其他轴的待测轴进行转动，转动到适当的角度后，再对其他轴进行转动并比较观察此时其他轴是否与模型初始的转动轴一致。从而得出轴旋转的带动情况，最后分析解释现象得出结论。

(二)旋转现象的观察

直接给Heading，Picth，Roll赋值，进而测试旋转轴的带动情况。

通过对模型进行测试转动，得到以下成果：

图5 ArcGIS Runtime中三个转动轴

(其中黄色轴为Heading轴，红色轴为Pitch轴，橙色轴为Roll轴)

Figure5ThreeRotatingaxesinArcGISRuntime

(The yellow axis is the Heading axis,the red axis is the Pitch axis,and the orange axis is the Roll axis)

图6 Pitch轴的旋转不带动Heading轴

图7 Pitch轴的旋转带动Roll轴

图8 Roll轴的旋转不带动Heading轴

图9 Roll轴的旋转不带动Pitch轴

图10 Heading轴的旋转带动Pitch轴

图11 Heading轴的旋转带动Roll轴

图中白线旋转轴为被带动后的旋转轴，其他颜色旋转轴与初始旋转轴一致。利用此方法观察ArcGIS Runtime的模型旋转，现象总结如下：

表一 ArcGIS Runtime中旋转轴的带动现象

(三)旋转现象的解释和旋转机制的确定

但ArcGIS Runtime的模型旋转并非如此复杂，当Pitch，Roll，Heading任意一个的值发生改变时，并不是基于上次的空间姿态改变相应的角度，而是计算机重新通过获取到的三个旋转角度进行计算空间姿态。通过上面的旋转现象可以看出，ArcGIS Runtime的旋转机制是带轴旋转的，在旋转的顺序上，后面轴的旋转是不会影响前面的旋转的，而现象中出现的不带轴的情况是因为该轴在旋转顺序的后面，导致每次改变处于顺序后面的旋转角度时，计算机都会重新通过旋转顺序计算模型空间姿态，处于顺序前面的旋转角度没有改变，因此后面的旋转轴与以前的一致，当计算到顺序后面的轴旋转时，由于顺序前面的轴已经旋转过了，而后面也没有该轴的旋转，因此造成了后面的旋转没有带动处于旋转顺序前面的轴旋转的假象，因此可以得出结论有不带轴旋转假象的旋转处于旋转顺序的后面，由此结论及该现象便可以推论出ArcGIS Runtime的旋转机制是Heading - Pitch - Roll顺序的带轴旋转。

在旋转顺序上，顺序后面的轴旋转将不会影响顺序前面轴的旋转，而顺序前面的轴旋转会带动后面旋转的旋转轴。当逆顺序的不带轴旋转时，由于是不带轴旋转，因此顺序前面的轴旋转不会影响顺序后面的轴旋转，此时讨论顺序后面的轴旋转是否带动顺序前面的轴也已经没有意义了，因为带不带动都不会影响顺序后面的旋转，正顺序的带轴旋转，顺序后面的轴旋转不会影响顺序前面的轴旋转，因此，两者影响顺序后面旋转的旋转轴带动情况是一致的，当对应轴的旋转角度一致时，两种旋转方法也将会达到一样的效果。因此可以得出结论，逆顺序的不带轴旋转效果等同于带轴旋转，这也为后面的旋转角矩阵解算提供了支撑。

就以ArcGIS Runtime的旋转机制为例，当逆顺序不带轴旋转时，Roll轴的旋转不带其他轴。Pitch轴的旋转，首先不会带动Heading轴，而Roll轴顺序上在Pitch轴前面，因此Pitch轴会不会被带动已经没有意义了(实际上是带动的)，因为不会影响后面的旋转，而这里为了方便比较就记为Pitch的旋转带动了Roll，而最后的Heading轴更是如此，会不会带动其他轴已经没有意义了，为了方便比较同样记为带动了Pitch轴和Roll轴，由此可以看出现象：

表二 逆顺序的不带轴旋转旋转轴的带动现象

该现象与ArcGIS Runtime的旋转现象一致，当对应轴的旋转角度一致时，两种旋转机制效果等同。

三、不同旋转机制旋转角的相互转换

(一)旋转矩阵

坐标变换，利用欧拉角描述一次平面旋转，见图12。

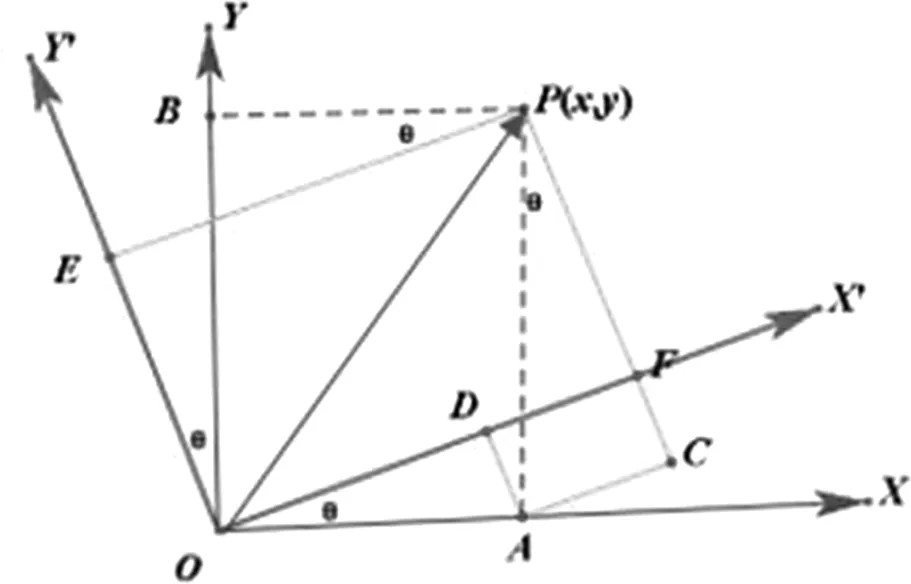
图12 坐标系间的变换关系

设坐标系绕O点旋转θ角后得到坐标系X′ OY′,空间中有一矢量OP在坐标系XOY中的坐标为r1，在坐标系X′OY′中坐标为r2,Z坐标未变，即有[4]：

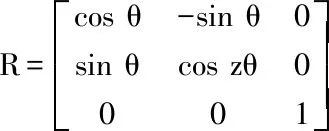
(1)

r2=R*r1

旋转矩阵是由9个元素组成的3×3的正交矩阵[5]。假设绕着Heading，Pitch，Roll旋转的角度为z，x，y，以此类推，则空间的三个旋转矩阵如下：

(2)

(二)旋转矩阵的左乘与右乘

空间的旋转矩阵是由多个单次旋转组成。如果第二次及以后的旋转是相对于基础坐标系来做的，则第二个及以后的旋转矩阵左乘之前的旋转矩阵。

如果第二次及以后的旋转矩阵是相对于前一次旋转后带动的坐标系，则第二次及以后的旋转矩阵右乘之前的旋转矩阵[6]。

而ArcGIS Runtime的旋转是带轴旋转的，因此旋转矩阵的组合是矩阵的右乘，假设在ArcGIS Runtime中绕着Heading，Pitch，Roll旋转的角度为z，x，y，则ArcGIS Runtime旋转矩阵为RHeading(z)RPitch(x)RRoll(y)。

(三)不同旋转机制旋转角的解算

ArcGIS Runtime的旋转矩阵是：

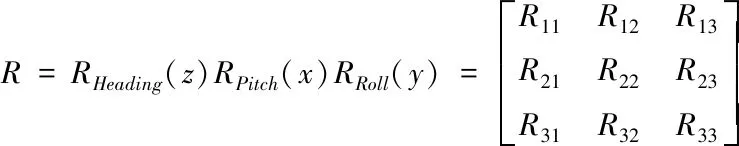
R11=cos y cos z-sin y sin x sin z

R12=-sin z cos x

R13=sin y cos z+cos y sin z sin x

R21=cos y sin z+sin y sin x cos z

R22=cos x cos z

(3)

R23=sin z sin y-sin x cos z cos y

R31=-sin y cos z

R32=sin x

R33=cos y cos x

从上列等式可以导出x,y,z的角度，公式如下：

y=arctan2(-R13,R33);

(4)

z=arctan2(-R21,R22)

这样便可以将任意的旋转机制的旋转角转换为ArcGIS Runtime旋转机制的旋转角了。假设电塔模型旋转机制的旋转角分别为Rotate_z,Rotate_x,Rotate_y，由于是不带轴旋转，旋转矩阵的组合是矩阵的左乘，而带轴旋转与不带轴旋转的相互转换是逆顺序旋转即可，因此该旋转矩阵如下：

P11=cos(Rotate_z)cos(Rotate_x)cos(Rotate_y)-sin(Rotate_z)sin(Rotate_y)

P12=-cos(Rotate_z)cos(Rotate_x)sin(Rotate_y)-sin(Rotate_z)cos(Rotate_y)

P13=cos(Rotate_z)cos(Rotate_x)

(5)

P21=sin(Rotate_z)cos(Rotate_x)cos(Rotate_y)+cos(Rotate_z)sin(Rotate_y)

P22=-sin(Rotate_z)cos(Rotate_x)sin(Rotate_y)+cos(Rotate_z)cos(Rotate_y)

P23=sin(Rotate_z)sin(Rotate_x)

P31=-sin(Rotate_x)cos(Rotate_y)

P32=sin(Rotate_x)sin(Rotate_y)

P33=cos(Rotate_x)

两个旋转矩阵都是使同一个初始姿态到同一个目标姿态，因此令R=P;则有:

y=arctan2(-P13,P33);

(6)

z=arctan2(-P21,P22)

由此可得由电塔的旋转机制的旋转角推导出ArcGIS Runtime旋转机制的旋转角。

通过该公式编写程序进行成果测试。

通过测试，无论当前是怎样的姿态，当转动三个旋转轴来改变Rotate_z,Rotate_x,Rotate_y的值时，在ArcGIS Runtime中刚好和塔模型旋转机制中的侧身，俯仰和指向相对应，通过这样的算法，将ArcGIS Runtime的旋转机制转化为了塔模型的旋转机制。这也说明了该公式和方法的正确性。

结语

三维模型姿态变换是三维模型应用领域的重要基础技术，随着三维模型在各行各业中的广泛应用，三维模型姿态变换技术也得到了飞速的发展[7]。而对于ArcGIS Runtime而言，三维模型姿态变换也影响用户的直观体验，模型的精准定位定姿态是三维应用最基本的保证。本文不仅给出了ArcGIS Runtime的旋转机制和不同旋转机制的旋转角转换，更是提供了观察旋转机制和不同旋转机制的旋转角转换的解算方法，这为更多的三维GIS开发者提供了支撑。