基于仿真分析和疲劳试验的服役铸铝横梁剩余寿命预测

窦伟元，张乐乐，周 挺，刘长青，张海峰

(1.北京交通大学 机械与电子控制工程学院，北京 100044；2.中车长春轨道客车股份有限公司，吉林 长春 130062)

国内某型动车组牵引电机采用体悬式，即通过万向轴将牵引力或制动力由牵引电机传递到轮对上的齿轮箱，该悬挂方式有助于降低一系簧下质量和轮轨作用力。由于电机系统质量较大，目前使用1对铸铝横梁共同承担电机系统重量，通过吊装方式连接于车体。铸铝横梁作为电机系统主要承载结构，整体呈树状对称拓扑形式，内部为空腔且带有肋板补强，设计寿命要求满足1.2×107km运营里程。铸铝横梁载荷来源包括由车体振动引起的大质量电机系统振动和电机自身驱动转矩，其中电机系统振动由轨道激扰引起，经转向架悬挂系统→车体传递到铸铝横梁；驱动转矩通过牵引电机经传动轴作用于铸铝横梁。铸铝横梁采用A357-T6铝合金铸造工艺，产品结构通常存在铸造缺陷(气孔、缩孔等)，初始缺陷状态复杂，且服役条件下所受载荷类型不唯一、产品未知的初始应力状态经服役后更加复杂，采用现有方法难以直接评估结构的累积损伤及剩余寿命。

目前，常用的轨道车辆结构疲劳性能的评估、预测方法包括实车测试、台架试验和仿真分析。实车测试成本较高，虽由真实线路作为测试条件的数据更加可信可靠，但对数据处理和过滤的要求较高；台架试验时依据标准或模拟实际激扰，通过作动器对结构进行加载，需合理设计载荷和输入信号；仿真分析成本最低，可用于探查复杂结构难以贴片位置的应力状态，其结果准确性依赖于仿真模型和边界条件。刘德刚等[1]基于实测载荷和材料S—N(其中S为应力幅值，N为疲劳寿命循环次数)曲线，通过有限元仿真分析转8A型转向架侧架危险部位并预测其疲劳寿命。王萌等[2]通过对线路实测载荷与动应力响应关系的解耦，实现对各载荷损伤影响程度的评估。张涛等[3]通过台架试验实现多频带激励条件下高速列车齿轮箱结构模态参数的识别。邬平波等[4]建立C64K型提速货车的非线性动力学模型，分析其在沈大线运行时转K2型转向架侧架的动态响应，并采用仿真方法对其疲劳寿命进行预测。朴明伟等[5]以高速列车刚柔耦合动力学模型为载体，研究空气弹簧特性对垂向振动的影响，结果表明曲线半径和垂向弯曲模态振型对车体垂向振动影响显著。王珊珊等[6]研究表明弹性模型对车体振动加速度影响显著，仿真结果与翟婉明等[7]进行的线路实测数据吻合较好。Miner准则作为等损伤线性疲劳累积损伤理论，未考虑载荷顺序及谱块中载荷间的相互影响[8]，嵇应凤等[9]研究表明随机谱块载荷下Miner准则精度与Manson准则和Corten-Dolan准则相当，且模型计算简单，易于应用。徐庆元等[10]基于Miner线性累积损伤模型研究无砟轨道钢筋混凝土结构在组合载荷下的疲劳特性。陈道云等[11]提出基于分段函数的结构动应力谱拟合方法，该模型应力谱采用Miner线性累积损伤模型的结果与实测谱损伤趋势一致。上述研究中针对寿命预测通常采用单一仿真或在线测试的方式，无法全面追踪结构应力状态或明确实际结构在承载条件下的累积损伤，可能导致预测结果偏于危险或过于保守。

本文针对服役一定里程后铸铝横梁剩余寿命预测，考虑其不确定性(初始损伤和内部缺陷未知、材料S—N曲线离散性等)，假设剩余寿命累积损伤可通过台架试验累积损伤进行等效表征，通过动力学和有限元仿真分析手段建立铸铝横梁应力谱，利用线性累积损伤评估方法实现对服役铸铝横梁剩余寿命的预测。以试验辅助验证仿真分析，由仿真全面评估铸铝横梁剩余寿命，该方法可为我国高速列车同等类型结构剩余寿命预测和优化设计提供依据。

1 服役铸铝横梁剩余寿命预测方法

结构寿命通常基于大量疲劳试验数据获得，而服役一定里程后的铸铝横梁具有残余应力状态复杂、累积损伤难以量化、内部初始损伤和缺陷未知等不确定性条件，导致难以基于已服役结构直接预测铸铝横梁剩余寿命。同时，Miner准则认为疲劳失效是不同(或相同)应力水平下产生的损伤通过线性叠加达到临界值时的结果，不同应力水平造成的损伤相互独立且仅与当次循环载荷大小有关而与时序无关。由此，服役铸铝横梁的全寿命累积损伤与分段累积损伤的关系为

D全寿命=D已服役+D试验+D未服役

(1)

式中：D全寿命为铸铝横梁由服役初始到最终出现宏观疲劳裂纹导致结构失效时的全寿命累积损伤；D已服役为铸铝横梁服役一定里程后的已服役累积损伤，此阶段产生的累积损伤未知；D试验为对服役一定里程后的铸铝横梁进行N次等幅循环台架疲劳试验产生的试验累积损伤，可通过试验和仿真分析进行量化；D未服役为实际线路条件下铸铝横梁可继续服役里程对应的损伤。

由式(1)可知，服役铸铝横梁剩余寿命对应的损伤可由D试验(试验后产生裂纹)或D试验+D未服役(未产生宏观裂纹)进行表征，可通过等幅循环载荷疲劳试验产生的累积损伤作为服役铸铝横梁剩余寿命的评估依据。具体地，若经107次加载，铸铝横梁产生疲劳裂纹，则可认为此时各评估点产生累积损伤对应的换算里程即为铸铝横梁最大剩余寿命；若经107次加载，铸铝横梁未产生疲劳裂纹，则采用此时各评估点累积损伤对铸铝横梁剩余寿命进行保守预测。

Miner线性累积损伤模型认为累积损伤与寿命(承载次数)的关系为

(2)

式中：D为累积损伤；ni为应力谱中各级应力水平下的循环次数；Ni为各应力水平下的疲劳寿命；p为应力谱级数。

对于具有不确定性影响因素的服役铸铝横梁，其剩余寿命(里程)为

(3)

式中：LPre为剩余寿命预测里程；DLimit为经过台架疲劳试验产生的累积损伤，作为寿命预测的损伤基准值；δj为实际线路中各工况占比；q为工况数；LSim为仿真分析计算的线路长度，km；Dj为与之对应的线路仿真工况累积损伤，由动力学和有限元分析建立应力谱，结合材料S—N曲线根据式(2)计算而得。

基于多体动力学模型分析铸铝横梁外载荷特性，将载荷作为经静载试验校验后有限元模型的边界条件进行瞬态响应分析，结合雨流计数法，建立各评估点应力谱；根据材料疲劳特性曲线，由上述疲劳试验获得累积损伤作为预测基准，结合仿真计算应力谱实现服役铸铝横梁剩余寿命预测。预测流程如图1所示。

图1 服役铸铝横梁剩余寿命预测流程

2 基于线路工况的服役铸铝横梁动态载荷

2.1 车体—铸铝横梁刚柔耦合模型

为获得服役铸铝横梁在实际线路工况下的动态载荷，建立弹性化车体—铸铝横梁动力学分析模型。服役铸铝横梁与牵引电机等组成体悬式电机系统，系统间相互作用使得铸铝横梁受载状态复杂，且由于铸铝横梁吊装于车体下方，以1阶垂向弯曲为主的车体弹性振动对铸铝横梁的影响不可忽视。

基于车体和铸铝横梁有限元模型，经自由度缩减生成弹性体模型，通过主节点与悬挂系统和电机系统匹配组成刚柔耦合模型，如图2所示。建立的刚柔耦合模型由弹性车体、弹性铸铝横梁、转向架系统、牵引电机系统及驱动轴等组成，同时考虑悬挂系统阻尼及轮轨接触等为非线性。

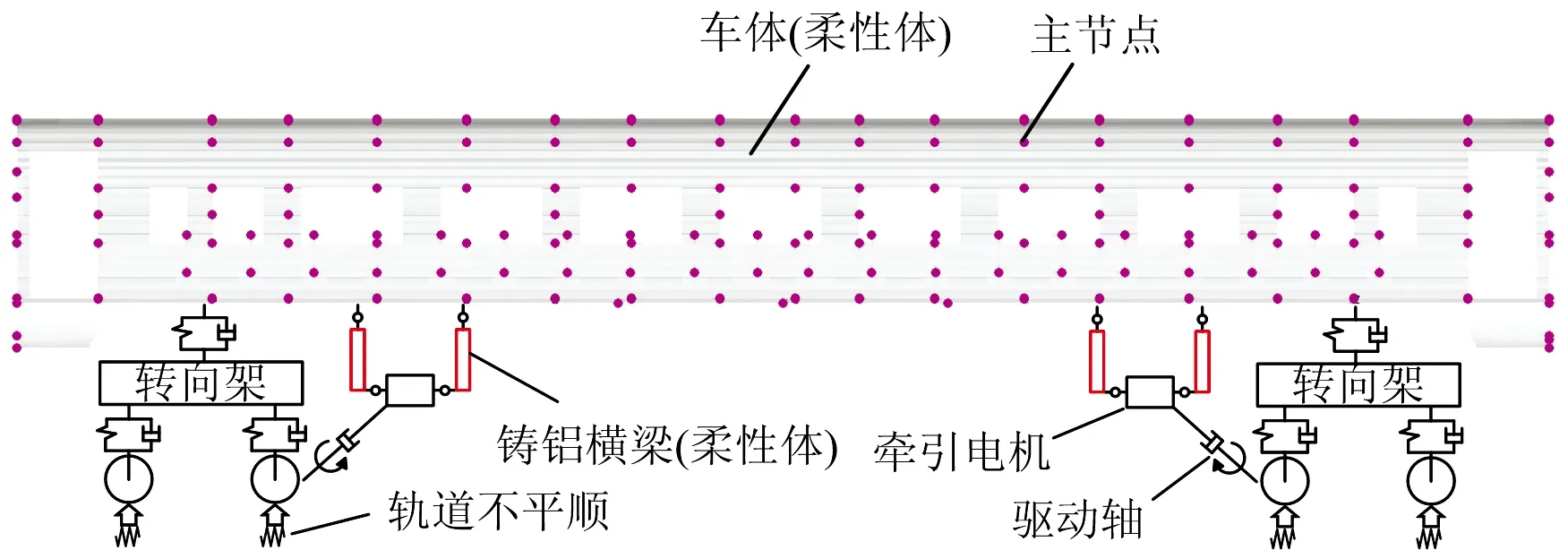
图2 车体—铸铝横梁刚柔耦合模型

车体和铸铝横梁前5阶全自由度和缩减自由度后的模态频率对比见表1。由表1可见，自由度缩减前后各阶模态频率误差均小于0.1%，缩减模型满足计算精度的需求。

2.2 线路工况及车体振动响应

该型车运营时速为250 km·h-1，采用国内200 km·h-1等级提速线路轨道谱[12]作为刚柔耦合模型线路激扰输入条件，其表达式为

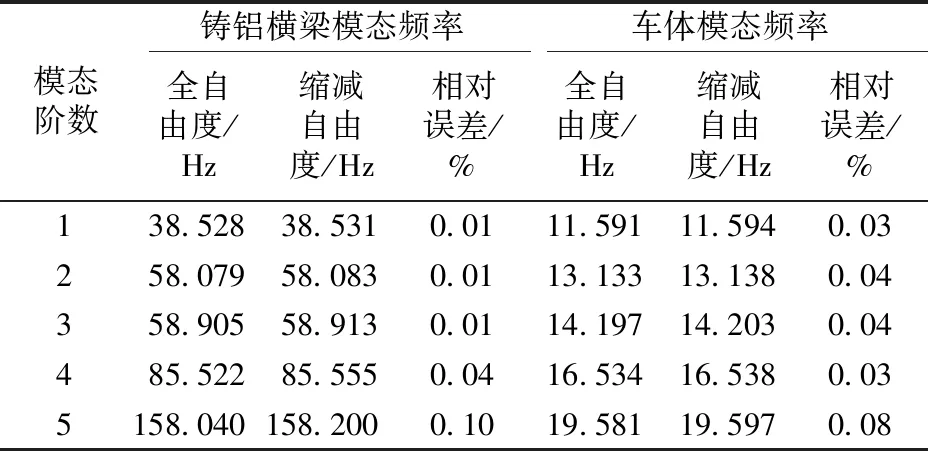
表1 车体和铸铝横梁的模态频率对比

(4)

式中：P(f)为轨道谱拟合函数；f为轨道激扰的空间频率；a，b，c，d，e，k均为轨道激扰特征参数，取值见表2。

表2 轨道激扰特征参数

国内某高速铁路7种典型线路工况(缓和曲线、曲线、直线段占比)见表3[13]。由表3可见，该线路中直线占比约70%，曲线占比约30%，其中小曲线半径(≥3 km)占比2%。

表3 某线路曲线占比统计

刚柔耦合模型在直线工况下车体地板中部位置的振动加速度如图3所示。由图3可见，车体垂向的振动加速度幅值整体高于横向，两者峰值分别为0.61和0.49 m·s-2；车体垂向振动加速度主要为分布在10 Hz以下的低频振动，而横向振动加速度是由频率为10与20 Hz的振动加速度叠加而成，2种振动形式分别由弹性车体的垂向和横向1阶振型引起。

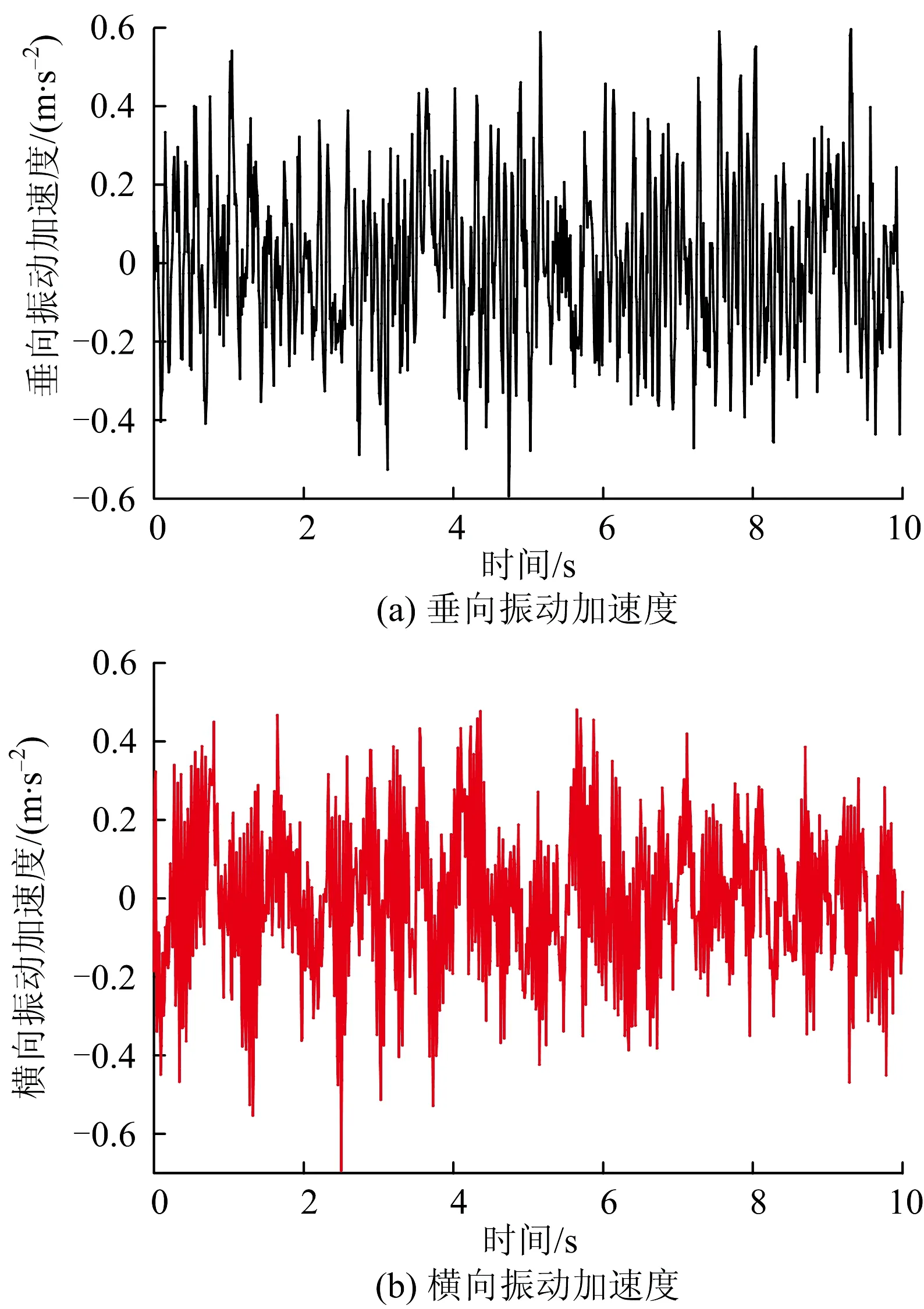
图3 刚柔耦合模型中车体振动加速度

2.3 铸铝横梁动态载荷

提取牵引电机与铸铝横梁间弹簧力元载荷时程曲线，可知作用于铸铝横梁的动态载荷由大到小依次为垂向、横向和纵向载荷，且垂向和横向载荷远大于纵向载荷，如图4所示。由图4可知，作用于铸铝横梁垂向载荷的频率高于横向载荷，两者均为非对称循环载荷；随着曲线半径的减小，垂向和横向载荷绝对椎均随之增大，其中垂向和横向载荷的最大值分别为-6 900和1 200 N，表明小半径曲线工况下铸铝横梁承受的动态载荷水平较大。

图4 不同线路工况下铸铝横梁动态载荷

3 铸铝横梁有限元模型及试验校验

铸铝横梁内部中空，中部腹板和电机支撑座位置通过加强筋肋板进行补强，顶部树形结构与车体地板和底架边梁通过螺栓固定，单侧两电机支撑座承载电机载荷，建立的静载分析铸铝横梁有限元模型如图5所示。忽略非主承载区细小几何特征，采用四面体单元进行网格离散，对应力集中和评估点位置进行渐进式网格加密，最小和最大网格尺寸分别为0.2和10 mm。疲劳试验条件下，对树形结构顶部施加全约束，分别采用PRETS179和CONTACT173单元施加螺栓预紧力和表面接触，通过两侧工装传递三向动载荷。采用线弹性模型，铸铝材料A357-T6主要力学参数见表4。

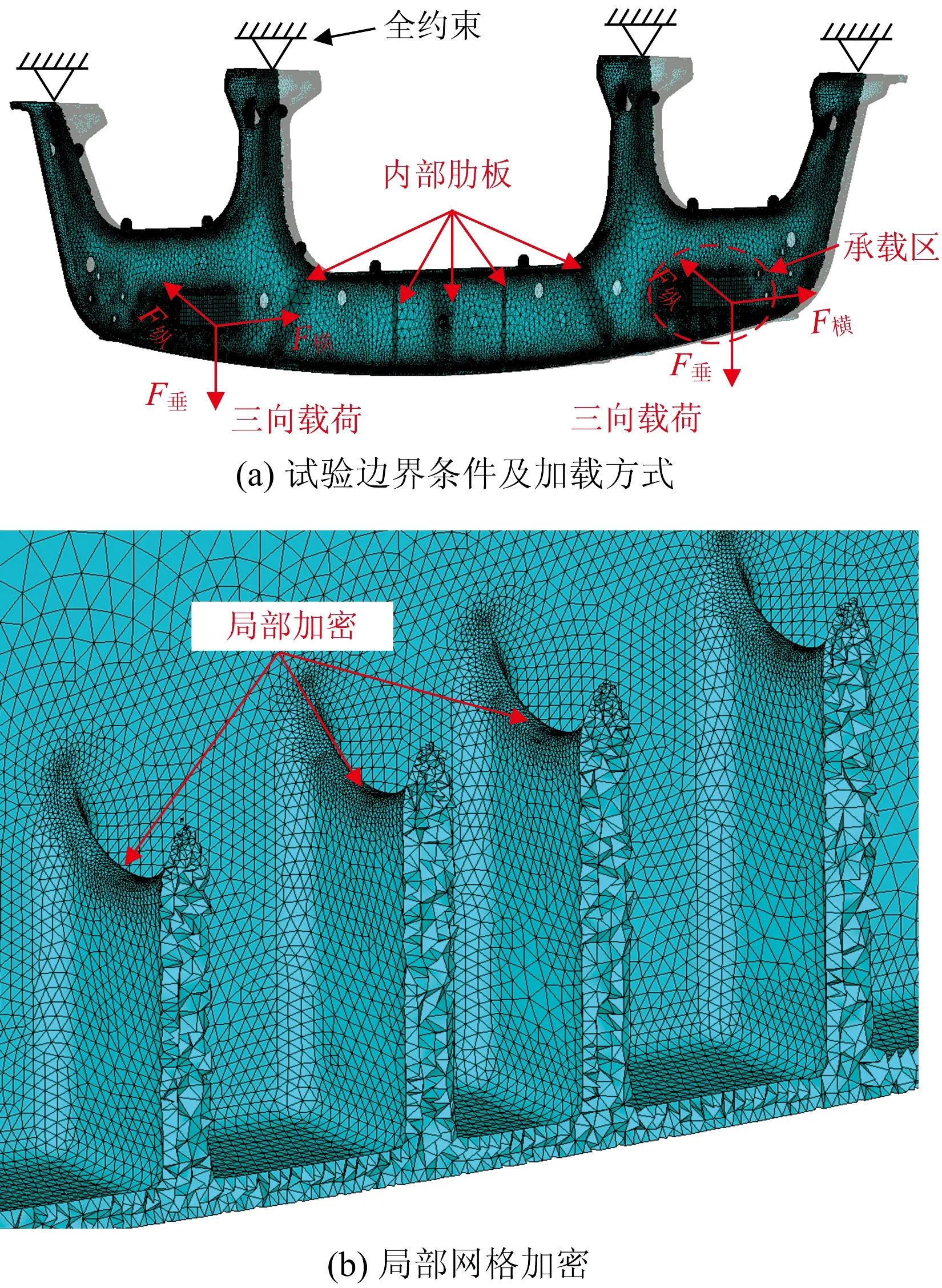
图5 静载分析铸铝横梁有限元模型

表4 A357-T6铸造铝合金力学性能参数

试验工装如图6所示，控制两侧三向作动器内油缸压力实现不同幅值水平和组合的静态载荷施加。根据探伤、初步仿真结果并考虑应力集中的影响，在铸铝横梁主承载区位置进行贴片并采集各载荷水平下的应力数据，各测点应力随载荷变化曲线如图7所示。

图6 工装约束及加载

图7 各测点应力随载荷变化曲线

在建立的铸铝横梁有限元分析模型施加试验工况相同载荷，根据贴片位置提取应力数据，并与试验结果对比，如图8所示。由图8可见，与试验应力对比，仿真结果中90%测点上应力的绝对误差在1 MPa以内，80%测点上应力的相对误差在10%以内，绝大部分仿真测点应力与试验数据吻合，表明铸铝横梁有限元模型的精度满足需求。

图8 铸铝横梁静载试验与仿真误差对比

4 基于瞬态分析的铸铝横梁结构应力谱

4.1 应力响应

为建立不同线路工况条件下铸铝横梁评估点应力谱，结合有限元瞬态仿真对铸铝横梁振动响应进行分析。实际线路工况下2根横梁配合使用，铸铝横梁的边界条件比试验工装稳定，因此在静载试验校验的有限元牛型上，在工装位置增加对称约束以模拟对侧结构的约束作用；载荷则输入线路工况(图4中的载荷曲线)获得的动态载荷，如图9所示。

图9 线路条件边界及加载

采用全积分求解器进行计算，各工况计算时长15 s，仿真步长0.01 s。计算结果表明，曲线半径的变化对应力分布云图影响较小，应力幅值随曲线半径减小而增加。t=3 s时刻铸铝横梁典型等效应力分布云图如图10所示。由图10可见，应力较大位置主要位于树状吊座过渡圆弧(评估点1)、内部补强肋板顶部(评估点2)和承重支座根部铸造圆角(评估点3)及过渡圆角(评估点4)等位置，选取以上位置作为评估点进行剩余寿命预测。其中评估点1应力最大，为17.2 MPa，该点等效应力时程曲线如图11所示。

图10t=3 s时铸铝横梁典型等效应力分布云图(单位：GPa)

图11 评估点1等效应力时程曲线

4.2 评估点应力谱

瞬态分析表明，铸铝横梁应力响应幅值较低，小幅值应力比例远高于大幅值应力，各评估点位置始终处于拉伸应力状态，即各点应力比大于0。由于最小主应力与最大主应力之比介于-0.25～0.25之间则可认为该点处于单轴应力状态[1]，因此，可采用雨流计数统计得到铸铝横梁各评估点二维载荷谱。此外，由于铸铝横梁各点应力状态通常为非对称循环应力，采用由对称循环载荷获得的材料S—N曲线(R=-1，平均应力为0)进行评估时，需通过Goodman方程修正平均应力的影响，即

(5)

式中：Sa为修正后应力幅；S-1为对称循环下材料疲劳极限；Sm为平均应力；SU为材料拉伸极限。

修正平均应力后，铸铝横梁4个评估点8级应力谱见表5。由表5可见，最大应力出现在评估点1处，约为2.14 MPa。

表5 评估点应力谱

5 服役铸铝横梁剩余寿命

5.1 铸铝A357-T6疲劳特性

铸铝横梁采用A357-T6铝合金铸造而成。由瞬态分析可知评估点位置处应力可近似为单轴应力，可采用材料S—N曲线评估其剩余寿命。文献[14]认为小尺度铸造缺陷对不同应力比下该铸铝材料疲劳特性影响不大，且其公布的应力比为-1时的疲劳试验数据，通过Basquin方程进行拟合，即

SmN=C

(6)

式中：m和C为材料常数，通过拟合获得。

截止106次循环时，材料S—N曲线如图12所示。一般将107次循环以后的S—N曲线视为水平直线，但会导致低幅应力损伤预测结果偏于危险[15]，而直接法[16]外推的S—N曲线远低于实测数据，安全裕度偏大，故基于欧洲ECCS和瑞典BSK标准中的2m-1指数法对S—N曲线进行外推。该方法采用2m-1斜率对5×106次循环以后的长寿命S—N曲线进行平滑外推，参数取值见表6。

图12 铸铝A357-T6疲劳寿命S—N曲线

表6 S—N曲线拟合参数

根据式(6)可得，铸铝A357-T6疲劳极限(疲劳寿命循环次为107次时)约为86 MPa。

5.2 服役铸铝横梁疲劳试验

铸铝横梁结构现阶段尚缺乏成熟的疲劳试验标准，综合考虑标准BS EN 12663《铁路应用—铁道车辆车体的结构要求》和标准IEC 61373《机车车辆设备冲击和振动试验标准》中对车体及其附属结构疲劳试验载荷和振动试验加速度的要求，设计铸铝横梁疲劳试验。垂向载荷动载系数取0.75，其余载荷按标准施加，试验载荷高于实测数据[7]和本文仿真值。

试验前，采用渗透染色法对结构表面进行探伤以明确初始状态，仅非主承载区存在2处小尺寸铸造缺陷，无表面宏观裂纹。通过MTS多通道协调系统对铸铝横梁进行三向加载，输入波形为5 Hz正弦曲线，三向载荷同相位施加，共计加载107次；通过铸铝横梁表面布置应变片，采集动应力数据，结果表明：加载过程中各测点以拉应力为主，个别位置存在压应力状态，测点最大拉应力为27 MPa，最大压应力为-5.8 MPa；所有测点应力平均值不为0，应力幅最高为16.35 MPa，80%测点应力幅值低于10 MPa。试验结束后，对铸铝横梁进行2次探伤，未产生表面宏观裂纹，局部铸造缺陷未产生裂纹扩展。

5.3 剩余寿命(里程)预测

铸铝横梁经107次等幅循环台架疲劳试验后未产生表面宏观裂纹，针对其剩余寿命预测，以评估点1为例：通过式(5)对非对称循环的平均应力进行修正，获得对称循环下应力幅和循环次数(疲劳试验取107次)，结合Miner线性累积损伤理论和材料S—N曲线获得此时该点的累积损伤DLimit作为铸铝横梁剩余寿命预测的基准损伤值；由表5中采用有限元仿真分析和雨流计数法获得评估点1的8级应力谱，通过式(2)和式(3)对其在仿真里程LSim下各工况的累积损伤进行计算，根据运营里程与累积损伤之间的线性比例关系，外推当线路工况累积损伤与台架试验累积损伤DLimit等效时的运营里程LPre作为铸铝横梁的剩余寿命里程。计算表明该服役铸铝横梁剩余寿命里程为6.41×1011km，仍高于铸铝横梁设计要求的最低寿命里程1.2×107km，见表7。

表7 铸铝横梁台架试验应力统计与剩余寿命里程预测

6 结 论

(1)考虑轨道激扰和牵引电机输入力矩，由动力学仿真获得铸铝横梁在线路条件下的外载荷，作为有限元模型输入条件，获得评估点应力时程曲线，通过雨流计数建立各点应力谱。由多级载荷中低的应力水平(经Goodman修正平均应力后评估点的最大应力幅为2.14 MPa)计算得到的累积损伤远低于损伤临界值。

(2)通过铸铝横梁静载试验对有限元模型进行校验，试验与仿真测点结果一致性较好，仿真模型精度满足计算要求。服役铸铝横梁疲劳试验结果表明：经107次等幅循环加载，结构未产生疲劳裂纹，试验条件下最大应力幅18.1 MPa(小于疲劳极限86 MPa)，以此计算的累积损伤作为剩余寿命预测基准条件。

(3)以分段累积损伤表征结构全寿命的方法可以避免服役结构初始不确定性条件的影响，同时提供剩余寿命预测所需的基准条件，并由试验和仿真结合的方法实现结构剩余寿命的预测。考虑材料S—N曲线外推方法和Miner准则通常偏于保守，以此时的累积损伤作为基准，剩余寿命预测结果偏保守；应力谱和损伤基准的计算均表明铸铝横梁设计大的安全裕度，符合与车体等寿命设计的要求，预测剩余寿命仍满足1.2×107km运营里程。