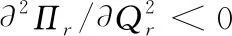基于“搭便车”行为的双渠道供应链库存竞争和促销策略
2019-08-19易超群万光羽
曹 裕,易超群,万光羽
(1.中南大学商学院,湖南 长沙 410083;2.湖南大学经济与贸易学院,湖南 长沙 410006)
1 引言
近些年,我国电子商务发展迅速。据中国电子商务研究中心数据表明,2017上半年中国电子商务交易额高达13.35万亿元,同比增长27.1%。其中,B2B市场交易额9.8万亿元,同比增长24%。网络零售市场交易额3.1万亿元,同比增长了34.8%[1]。随着电子商务和信息技术的快速发展,越来越多的制造商,例如Dell,IBM,Nike,Apple等通过传统零售渠道和网络渠道将产品销售给消费者[2-5]。与此同时,消费者行为也呈现出新的特点。这种环境给双渠道供应链发展主要带来了两个方面的影响:渠道间竞争和跨渠道搭便车现象。由于传统零售渠道和网络渠道的产品本质上是相同的,因此消费者在购物时会在传统零售渠道和网络渠道进行选择[6-9]。而且因为同一种产品在传统零售渠道和网络渠道间的相互替代性,因此当其中一个渠道缺货时,消费者会以一定的概率转向另一个渠道购买产品[10]。同时随着网络渠道的引入,传统供应链系统受到巨大冲击,双渠道供应链系统的发展使得搭便车现象即消费者和拥有在线渠道的制造商搭乘线下零售商便车,迅速增加。在双渠道消费者搭便车行为发生的过程中,没有提供促销努力的制造商也是搭便车者,他们没有付出促销努力,却间接地享受了付出促销努力的零售商而带来销售的增加。尤其当“搭便车”行为程度很大时,零售商付出促销努力的动机会很小。也就是说,“搭便车”行为会影响零售商促销策略。总之,渠道间库存竞争和“搭便车”行为下零售商促销努力的双渠道供应链问题是制造商和零售商不得不面临的重要问题。
双渠道供应链问题一直以来是学术界众多学者关注的重点。其中不少学者研究了双渠道供应链的协调及契约设计问题[11-14]。另外有不少学者研究了双渠道缺货替代问题。在双渠道中,因同种产品渠道间的相互替代性,因此当某一渠道缺货时,顾客通常会转移到另一个渠道购买。研究表明,当消费者所偏好的产品购物渠道缺货时,约有21%~43%的消费者会转向其他渠道购买产品[15]。所以这类现象引起了很多学者的关注,其中有部分学者研究了随机需求下的双渠道缺货替代问题。侯琳琳和邱菀华[16]研究了随机需求下,不同渠道间存在缺货替代的传统渠道和直销渠道间的库存竞争问题。雷延军和李向阳[17]研究了随机需求下,不同渠道间存在缺货替代的两级双渠道供应链的马尔科夫库存优化模型。Chiang和Monahan[18]研究了随机需求下,不同渠道间存在缺货替代的两层双渠道供应链库存管理策略。Takahashi等[19]研究了随机需求下,不同渠道间存在缺货替代的两层双渠道供应链模型的库存控制策略。Yang Jiaquan等[20]研究了随机需求下,不同渠道间存在缺货替代的双渠道库存竞争。当两种渠道并存时,不可避免会出现“搭便车”问题。例如,顾客在购买衣服时先去实体店了解衣服的款式和价格并试穿,最后去网络渠道以更低的价格购买。在此基础上,本文考虑了缺货替代和“搭便车”行为对渠道间库存竞争和零售商促销策略的影响。
消费者基于服务的搭便车行为普遍存在于现实生活中。当传统零售实体店开展各种促销活动时(如进行专业讲解、提供免费体验等),传统零售实体店的促销活动使消费者可以先享受传统零售实体店提供的讲解服务并体验产品性能,然后转移到网上渠道以较低的价格购买产品。Baal和Dach[21]研究发现,在实体零售渠道和网络渠道构成的双渠道中有高达20%消费者采取“搭便车”行为。随着网络渠道的引入,消费者“搭便车”现象迅速增加。这一现象引起了国内外学者的广泛关注。其中不少学者研究了双渠道供应链系统中的“搭便车”问题。周建亨和赵瑞娟[22]研究了搭便车效应影响下双渠道供应链信息披露策略。He Rongyao等[23]研究了消费者搭便车对双渠道闭环供应链中碳排放的影响。网络渠道和传统零售渠道并存的双渠道供应链将成为一种长期的市场格局,而这类供应链的促销策略也一直是学术界关注的重点。李建斌等[24]研究了零售商之间存在价格竞争和双向搭便车情形下双渠道供应链最优定价与销售努力水平决策。浦徐进和龚磊[25]研究了消费者“搭便车”行为影响下的双渠道供应链定价和促销策略。Xing Dahai和Liu Tieming[26]研究了消费者“搭便车”行为影响下供应链销售努力协调。尽管国内外已有不少文献研究了“搭便车”行为下的促销策略,但由于分析的复杂性,很少考虑需求随机情况。而本文将研究扩展到随机需求,研究了双渠道随机需求下,制造商及消费者都存在搭传统零售商服务便车的双渠道库存竞争和零售商促销努力策略。
现有文献中,部分考虑了随机需求下渠道间缺货替代问题,部分考虑了确定性需求下“搭便车”行为影响下促销策略问题。但是没有同时考虑渠道间缺货替代和“搭便车”这两种行为。然而在现实生活中,“搭便车”行为和渠道间缺货替代行为广泛存在。因此,本文研究了“搭便车”行为和缺货替代行为并存的双渠道库存竞争和零售商促销努力策略,同时把需求扩展到随机需求,分析了分散式和集中式决策双渠道供应链两种模式下“搭便车”行为程度和缺货替代率对零售商促销努力水平和其最优订购量及制造商最优库存量的影响。
2 模型
本文考虑由单个风险中性的制造商和单个风险中性的零售商组成的双渠道两级供应链系统,其中制造商通过传统零售渠道和自身网络渠道销售同一种产品。鉴于同一种产品在传统零售渠道和网络渠道间的相互替代性,即当其中一个渠道缺货时,一定比例的顾客会转向另一渠道购买产品[27]。同时,考虑到“搭便车”行为的影响,即零售促销努力不仅能提高自身渠道需求,也会提高制造商网络渠道需求。鉴于此,本文研究双渠道供应链系统随机需求下“搭便车”行为和渠道间缺货替代行为对供应链库存竞争与促销决策的影响。
在销售周期开始之前,零售商首先决策促销努力水平S,紧接着向制造商订购库存量Qr,同时制造商决定自身网络渠道销售的库存量Qm。在该双渠道供应链系统中,传统零售商以单位产品批发价格w从制造商购买产品,并以零售价格pr将该产品销售给顾客且提供促销努力水平S,其促销努力成本为ηS2/2[3],η为促销努力成本因子。同时,制造商在自身网络渠道以零售价格pm将该产品销售给顾客,并通过第三方物流将产品送至消费者,其交货前置期为l,其中制造商所需支付成本h/(2l2)[20],h为交货前置期成本因子。传统零售渠道和制造商在线渠道单位产品成本分别为cr和cm。本文假设所有价格[20, 27]和交货前置期[28]是外生的。在期末,零售商和制造商分别以单位产品期末残值sr和sm(sr
考虑到“搭便车”行为和渠道间缺货转换行为,本文参考Yang等[20]、浦徐进和龚磊[25]、Geng和Mallik[27]建立需求函数:
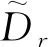
本文用下标r和m分别表示零售商和制造商相关参数;上标d和c分别表示分散式决策和集中式决策下相关参数;“*”表示最优解。
2.1 分散式决策双渠道供应链模型
本节考虑分散式决策双渠道供应链,制造商和零售商各自以收益最大化为目标决策自己的最优策略。
分散式决策下零售商期望收益Πr为:
Πr=prEmin(Qr,Dr)+srE(Qr-Dr)+-wQr-ηS2/2
(1)
分散式决策下制造商期望收益Πm为:
Πm=(w-cr)Qr+pmEmin(Qm,Dm)+smE(Qm-Dm)+-cmQm-h/(2l2)
(2)
下面应用逆向推导法探讨制造商和零售商最优解。首先在给定的零售商促销努力水平条件下,证明解的存在与唯一性,接着求解出最优制造商库存水平和零售商最优订购量,最后探讨零售商最优促销努力水平满足的条件。
定理1(1)分散式决策下,对给定的零售商促销努力水平,零售商传统零售渠道和制造商网络渠道的库存竞争存在唯一的纯策略纳什均衡。
(2)对给定的零售商促销努力水平,分散式决策下零售商期望收益是其订购量的严格凹函数;制造商期望收益是网络渠道库存量的严格凹函数。
(3)分散式决策下传统零售渠道中零售商促销努力水平Sd*满足下列条件:
其中
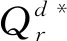
下面考虑零售商促销努力水平、“搭便车”行为程度及渠道替代率对零售商订购量和制造商网络渠道库存量的影响。
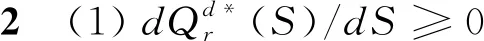
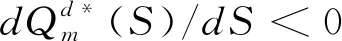
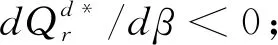
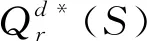
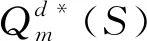
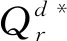

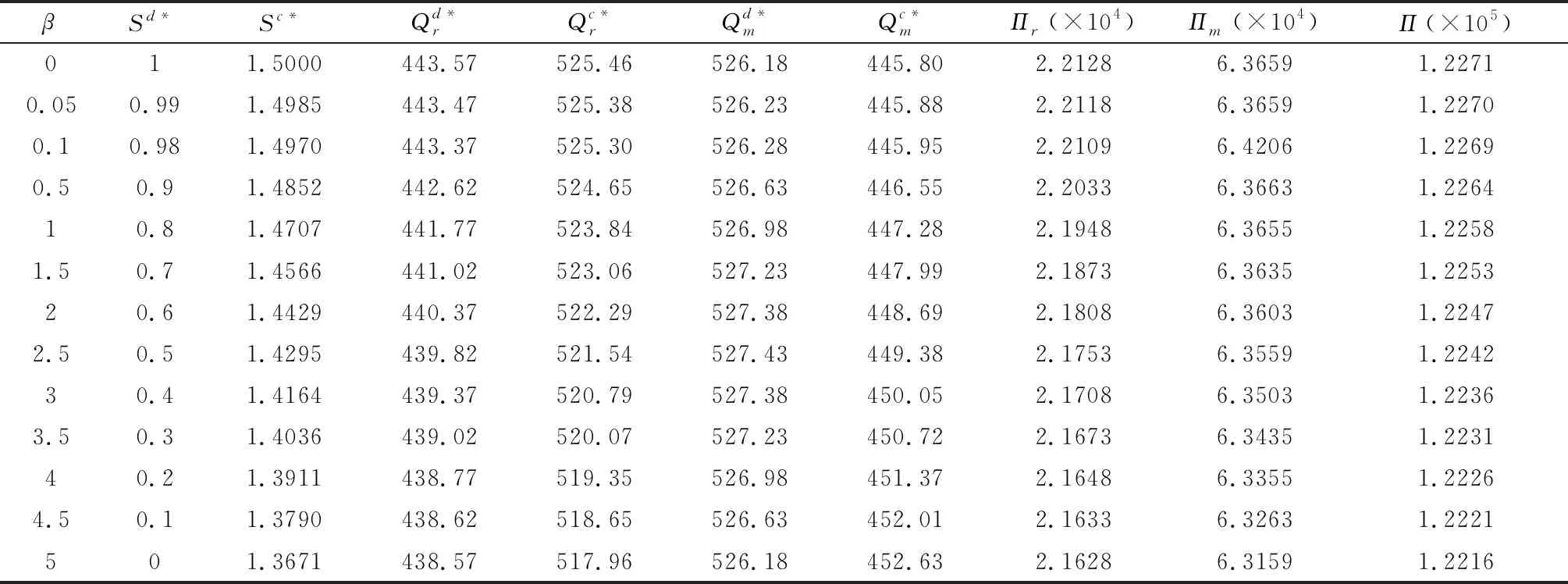
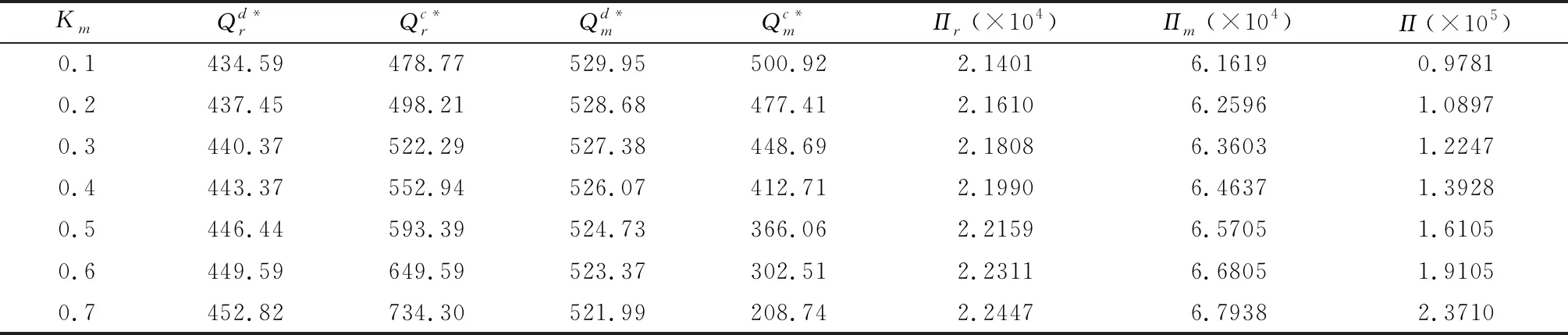
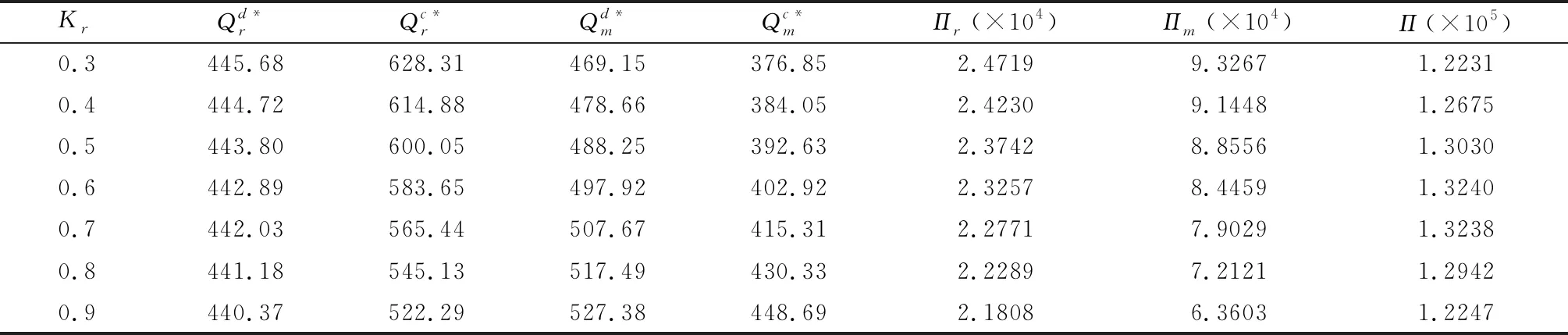
Qr-(r-β)S-λl<θ Qm-βS+vl<θ 假设传统零售渠道和网络渠道都为制造商所拥有或控制,则制造商和零售商将共同追求整个供应链利润最大化。因此Π=Πr+Πm,其中Πr,Πm分别满足(1)(2)式。 定理3(1)集中式决策下,对给定零售商促销努力水平S,整个供应链期望利润Π是Qr和Qm的严格凹函数。 (2)集中式决策下,零售商最优促销努力水平Sc*满足条件: Sc* 本节分析分散式决策和集中式决策下“搭便车”行为程度、传统零售渠道替代率、网络渠道替代率对零售商最优促销努力水平、零售商最优订购量、制造商网络渠道最优库存量、零售商收益和制造商收益、及供应链期望利润的影响。 下面分析“搭便车”行为程度β对零售商订购量、制造商网络渠道库存量以及利润函数的影响。参数设置如下:传统零售渠道替代率Kr=0.9,网络渠道替代率Km=0.3,其他基本参数不变。 由表1可知(1)分散式决策和集中式决策下,随着“搭便车”行为程度增加,零售商的最优促销意愿都在不断减少,且集中式决策下零售商最优促销努力水平Sc*大于分散式决策下零售商最优促销努力水平Sd*。特别地,当所有顾客“享受”完促销服务后都转移到网络渠道购买时,分散式决策下零售商不愿做出促销努力,但集中式决策下零售商仍愿意付出促销努力。 (4)分散式决策下零售商期望收益Πr随着“搭便车”行为程度β增加而减少;同时制造商期望收益Πm随着“搭便车”行为程度β的增加先增加而减少。在集中式决策下,供应链期望收益Π随着“搭便车”行为程度β增加而减少。对于不同的“搭便车”行为程度β,集中式决策下供应链期望Π收益大于分散式决策下供应链期望总收益Πr+Πm。 表1 “搭便车”行为程度(β)的敏感性分析 首先分析网络渠道替代率Km对零售商订购量、制造商网络渠道库存量以及利润函数的影响。参数设置如下:“搭便车”行为程度β=2,传统零售渠道替代率Kr=0.9,其他基本参数不变。 (2)分散式决策下,零售商期望收益Πr和制造商期望收益Πm随着网络渠道替代率Km增加而增加。集中式决策下,供应链期望收益Π随着网络渠道替代率Km增加而增加。对于不同的网络渠道替代率Km,集中式决策下供应链期望Π收益大于分散式决策下供应链期望总收益Πr+Πm。 表2 网络渠道替代率(Km)的敏感性分析 表3 传统零售渠道替代率(Kr)的敏感性分析 下面分析传统零售渠道替代率Kr对零售商订购量、制造商网络渠道库存量以及利润函数的影响。参数设置如下:“搭便车”行为程度β=2,网络渠道替代率Km=0.3,其他基本参数不变。 (2)分散式决策下,零售商期望收益Πr和制造商期望收益随着传统零售渠道替代率Kr增加而减少。集中式决策下,供应链期望收益Π随着传统零售渠道替代率Kr增加而增加。对于不同的传统零售渠道替代率Kr,集中式决策下供应链期望Π收益大于分散式决策下供应链期望总收益Πr+Πm。 本文建立了由一个制造商和一个零售商组成的双渠道供应链模型,研究了随机需求下“搭便车”行为和渠道间缺货替代行为对供应链库存竞争与促销决策的影响。证明了渠道竞争纯策略纳什均衡结果的存在和唯一性,分析了零售商促销努力水平、“搭便车”行为程度和缺货替代率对零售商最优订购量和制造商最优库存量的影响,并在假设传统零售渠道与网络渠道的潜在市场规模服从均匀分布的前提下,求出了分散式决策下零售商最优促销努力水平且分析了“搭便车”行为程度对零售商最优订购量和制造商最优库存量的影响。随后建立了集中式决策双渠道供应链模型,分析了零售商最优订购量和制造商最优库存量对整个双渠道供应链期望利润的影响,并在假设双渠道潜在市场规模服从均匀分布的前提下,求出了集中式决策下零售商最优促销努力水平且比较了分散式决策下零售商和集中式决策下零售商最优促销努力水平。 主要研究结论有:1)分散式决策下,网络渠道缺货会提高零售商的最优订购量,同样零售渠道缺货时,制造商会为网络渠道提供更多的库存;而“搭便车”行为对零售商与制造商订购量的影响则取决于渠道替代率的变化,但“搭便车”行为会降低零售商促销努力水平。特别地,在假设传统零售渠道与网络渠道的潜在市场规模服从均匀分布的前提下,“搭便车”行为程度越高,零售商需订购更少的最优产品。然而对于制造商而言,其网络渠道最优库存量取决于市场需求对传统零售渠道中促销努力水平的弹性系数。2)集中式决策下,对给定零售商促销努力水平,整个双渠道供应链期望利润是零售商订购量和制造商库存量的严格凹函数。3)数值分析发现,分散决策下制造商的最优库存量大于零售商最优订购量,而在集中式决策下零售商最优订购量大于制造商最优库存量;在不同的“搭便车”行为程度、传统零售渠道替代率、网络渠道替代率下,集中式决策下供应链期望收益大于分散式决策下供应链期望总收益。 附录: 定理1证明:(1)令 其中 =-η<0,令dΠr/dS=0得证。 推论2证明:由于 dQr(S*)/dβ=(dQr/dS)·(dS*/dβ)+∂Qr/∂β =-2(r-β)(pr-w)/η<0 同理dQm(S*)/dβ=(r-2β)(pr-w)/η。因此当0≤β≤r/2,dQm(S*)/dβ≥0;r/2<β≤r,dQm(S*)/dβ<0。 定理3证明:(1)易知∂2Πr/∂Qr∂Qm=∂2Πr/∂Qm∂Qr且∂2Πm/∂Qm∂Qr=∂2Πm/∂Qr∂Qm,类似Yang Jiaquan等[20]易证(1)成立。(2)通过对零售商期望收益Π关于S求一阶导数并令其等于零和隐函数定理可得零售商最优促销努力水平Sc*所满足的条件。 推论3证明:易知当θ>β2(pm-sm)/η时,d2Π/dS2=(β2(pm-sm)-θη)/θ<0。令dΠ/dS=0可得最优促销努力水平Sc*。

2.2 集中式决策双渠道供应链模型
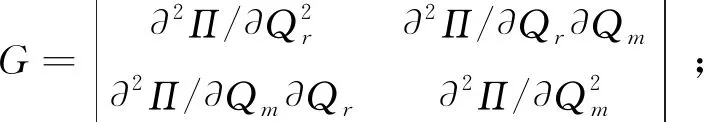
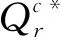


3 数值模拟
3.1 “搭便车”行为程度敏感性分析
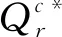
3.2 替代率敏感性分析
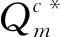
4 结语