异参离散广义Nash汇流模型及应用

闫宝伟，李正坤，霍 磊，张 俊，杨文发

（1.华中科技大学 水电与数字化工程学院，湖北 武汉 430074；2.长江水利委员会 水文局，湖北 武汉 430010）

Nash 瞬时单位线作为流域汇流的经典理论，在水文学发展历程上具有里程碑意义［1］，极大地推动了流域汇流理论的发展，是目前应用最为广泛的汇流计算方法之一。作为地表汇流的通用方法，Nash 瞬时单位线同样适用于河道汇流，闫宝伟等［2］基于Nash 瞬时单位线推导了河道洪水演算的完整公式，将河槽初始蓄水量的退水过程包含进来，创建了广义Nash 汇流理论［3］，并进一步建立了离散广义Nash 汇流模型，将下游河道出流表达为时段初、末入流量与当前及之前若干时刻出流量的线性组合，系数由S 曲线唯一确定［4］。S 曲线是Nash 瞬时单位线的积分函数，表征的是单位持续入流经过n 个相同线性水库的连续调节，在出口断面形成的出流过程［5］。调蓄参数K 是反映河道洪水传播时间的参数，与河道地形（坡降和断面形状）有关，这n 个水库具有相同的参数K，意味着河道的地形变化比较均匀，当地形变化较大时，各个水库的参数K 也将不同，此时宜采用异参瞬时单位线及其形成的异参S 曲线［6］，相应的，离散广义Nash 汇流模型将演化为异参离散广义Nash 汇流模型。非零初始条件下，高阶异参Nash 汇流系统微分方程的求解将变得非常困难，致使异参情形下广义Nash 汇流公式难以通过求解微分方程的方式直接获得。本文将另辟新径，通过对离散广义Nash 汇流模型的概念解析和数学推导，构建异参离散广义Nash 汇流模型，并分析其应用效果。

1 离散广义Nash 汇流模型的概念解析

根据闫宝伟等［4］的研究，离散广义Nash 汇流模型的计算公式为：

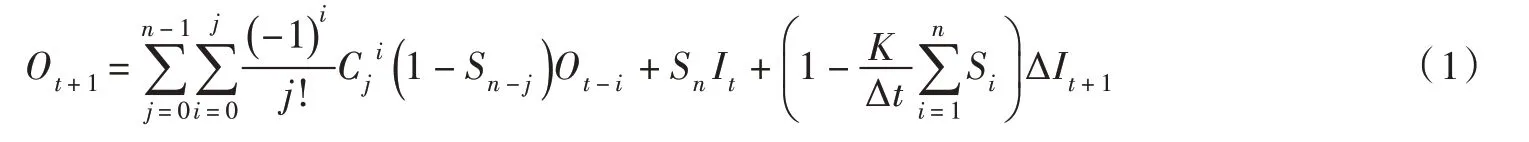
式中：为组合数计算公式；Ot±i为河段在t±iΔt 时刻的出流； Δt 为计算时段长； It为河段在t 时刻的入流； ΔIt+1为时段［t，t+Δt］内的入流增量；n、K 为模型参数；Si由下式计算：

根据S 曲线的定义，Si表示持续单位入流经过i 个水库的连续调节在时段末形成的出流。离散广义Nash 汇流模型的计算公式表明，下游断面的出流是由式（1）右边三项组成，其中第一项表示河槽当前蓄水量的退水流量，是由每个水库的初始蓄水量经由后面水库调蓄后形成流量的叠加；第二项表示当前入流经河槽调蓄形成的出流，由Si的定义知，其表示当前入流It持续不变时经过n 个水库的连续调节在时段末形成的出流；第三项表示时段初、末的入流增量经河槽调蓄形成的出流，由Si的定义和线性水库的蓄泄关系知，KSi表示持续单位入流时每个水库在Δt 时段内的蓄水量，则表示单位入流形成的槽蓄量的比例，则表示流出河槽水量的比例。概括来讲，下游断面的出流是由留在河槽中的“旧水”和上游入流的“新水”产生的。“新水”一部分流出下游断面，成为出流的一部分，另一部分则留在河槽中补充“旧水”，“旧水”消退，成为出流的另一组成部分，如此循环往复，则形成了下游断面的出流过程。

2 异参瞬时单位线及其S 曲线

流域的调蓄性能受地理特征的影响，具有空间异质性。Nash 瞬时单位线将流域的调蓄作用等效为多个相同线性水库的连续调节，对于地形变化较均匀的流域，这种概化有一定的合理性，而对于地形变化比较大的流域，调蓄作用的空间差异受地形地貌影响将更加显著。为考虑流域调蓄作用的空间异质性，Singh［7］提出了两个线性水库调蓄作用不同，即参数K 相异时的瞬时单位线。Bhunya 等［8］提出了两个水库的K 成比例时的瞬时单位线。张文华等［6］则进一步推导了n 个水库相异情形下的异参瞬时单位线：

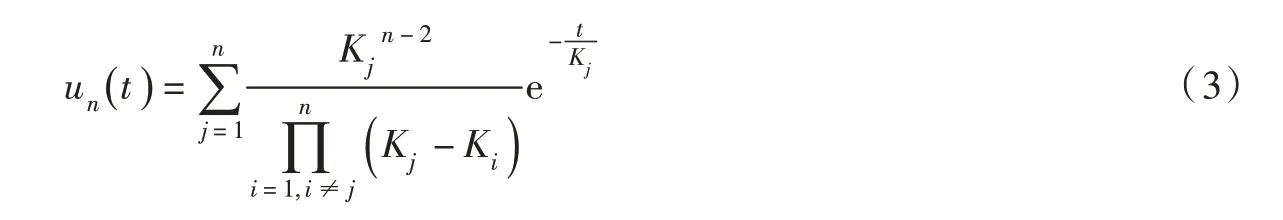
其中，Ki（i=1，…， n）为第i 个水库的调蓄参数（此处为正向编号，即最上游水库编号为1，最下游水库编号为n）。相应的，由异参瞬时单位线形成的异参S 曲线为：

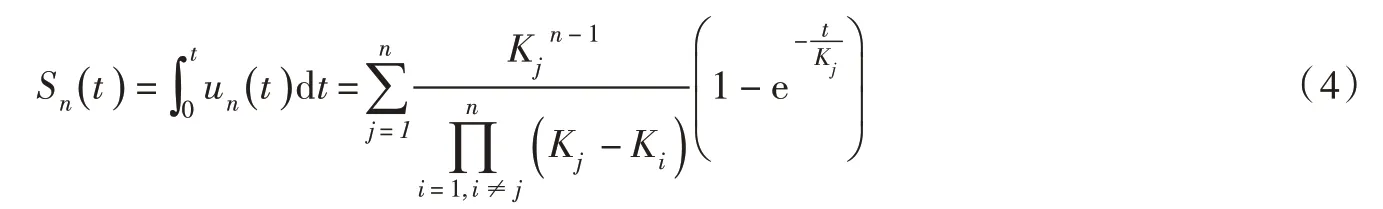
则Sn(t)表示1 个单位的持续入流经过n 个不同调节性能水库的连续调节，在出口断面形成的出流过程。若进一步定义滞蓄曲线，有：

则Rn′(t)=1-Sn(t)，表示1 个单位持续入流在流经这n 个水库时，滞留在这些水库或流域的流量过程。

异参瞬时单位线是对流域调蓄作用的更精确的概化，是Nash 瞬时单位线在理论上的进一步拓展，由于其考虑了调蓄性能的空间异质性，对于地形变化较大的流域，尤其适用。离散广义Nash 汇流模型是在Nash 瞬时单位线的基础上发展而来的，致使其在河道地形变化较大河段应用时有其理论局限性，异参瞬时单位线的引入可以反映各子河段对洪水调节性能的差异，从而提高整个河段洪水的模拟精度。

3 异参离散广义Nash 汇流模型

离散广义Nash 汇流模型的概念解析表明，下游断面的出流是由留在河槽中的“旧水”和上游入流的“新水”产生的，分别用Oold和Onew表示，则：

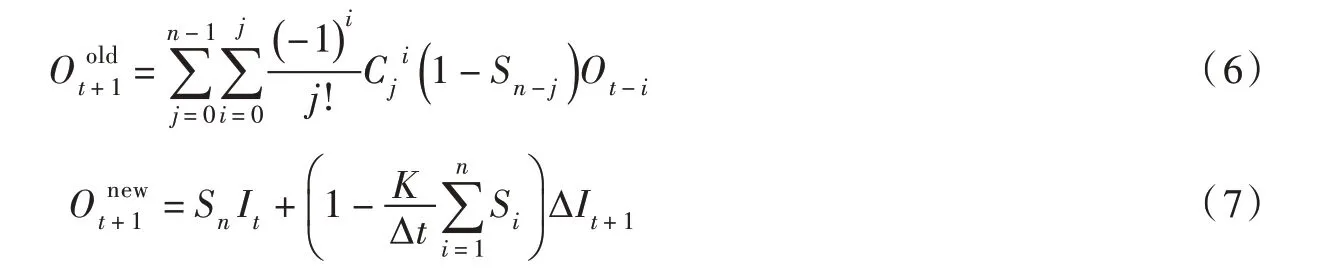
对于异参线性水库系统，由于Sn（t）表示单位持续入流经过n 个不同调节性能水库的连续调节，在出口断面形成的出流过程，则由线性水库的蓄泄关系可知，KiSi表示持续单位入流时第i 个水库在△t 时段内的蓄水量，则表示流出河槽水量的比例。因此，异参情形下上游入流，即“新水”产生的出流为：

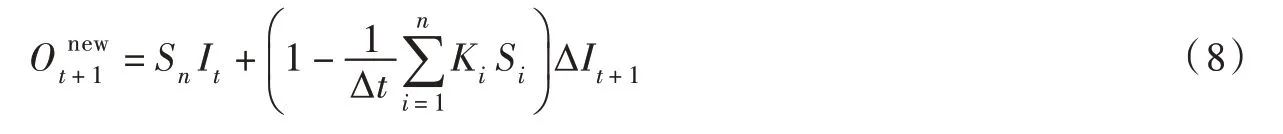
由此，通过离散广义Nash 汇流模型的概念解析，即可演绎出“新水”形成的出流Onew，下面继续分析河槽中的“旧水”产生的出流Oold。简便起见，假设最下游水库编号为1，最上游水库编号为n，即对这n 个水库进行逆向编号，则由水量平衡方程可得第i 个水库的调蓄方程为：

基于广义Nash 汇流理论，河槽当前蓄水量的消退过程是各水库当前蓄水量经后面水库连续调节后叠加而成。由式（9）可知，各水库当前时刻的出流量分别为：

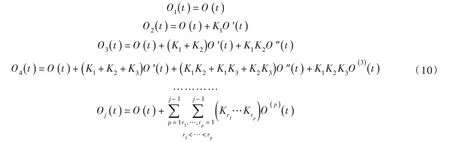
由线性水库的概念可知，第j 个水库当前时刻的蓄水量为KjOj(t)，将其作为瞬时入流注入河道，形成的时段末出流为KjOj(t)uj(Δt)，则所有水库当前蓄水量形成的时段末出流为：

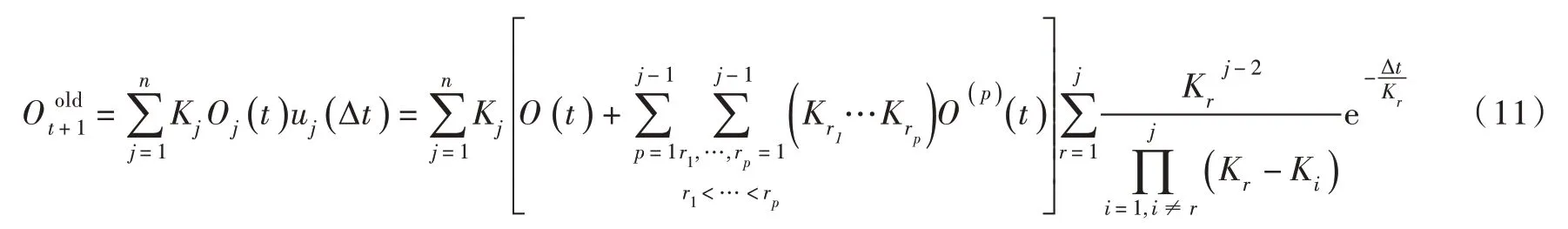
式（11）表明，该退水过程最终可以表达为当前时刻O(t) 的0～（n-1）阶导数的线性组合，即

式中， Ap(p=0，…，n-1) 分别为O(t)各阶导数的系数，则：

同理，可得：

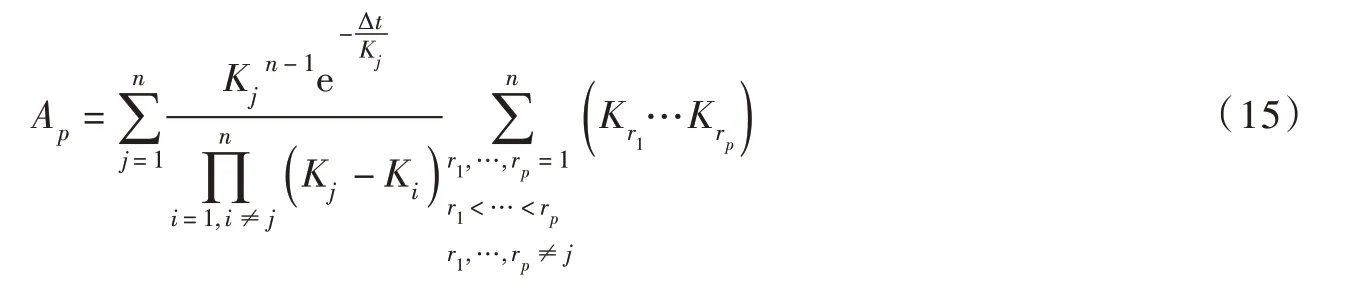
Ap是在逆向编号的情形下推导得出的，其计算公式表明，Ki具有对称性，因此，正向编号情形下，Ap的计算公式同式（15）相同，由此保证了Oold与Onew是在同一编号系统下进行计算的。采用前向差分近似计算O（t）的各阶导数，即：

若进一步定义无量纲参数：

则当p=0 时，结合式（5）滞蓄曲线的定义，可知R0=Rn′(Δt)，表示1 个单位的持续入流流经n 个水库时在Δt 时刻的滞蓄流量。当p＞0 时， Rp的物理含义尚需进一步研究。

联立式（12）、式（16）与式（17），可得：

根据离散广义Nash 汇流模型的概念解析，下游断面的出流是由留在河槽中的“旧水”和上游入流的“新水”共同产生的，则有：

该式即为异参离散广义Nash 汇流模型的计算公式，可以看出，它与离散广义Nash 汇流模型具有相同的结构。

4 实例分析

由模型的结构可知，异参离散广义Nash 汇流模型更加适用于河道地形变化较大的河段，选取汉江中游黄家港-襄阳河段进行模型的应用研究。黄家港水文站位于丹江口水利枢纽坝址下游6 km 处，为丹江口水库出库控制站，集水面积为95 217 km2；襄阳水文站位于丹江口水库下游111 km 处，是汉江中游的重要控制站，集水面积为103 261 km2，地理位置及河道形势如图1所示［9］。黄家港-襄阳河段地处丘陵平原区，山丘阶地及人工束窄段与平原宽谷段相间分布，在平面上呈明显的藕节状，宽段主泓摆动较大，洲滩较多，窄段较单一［9］，断面形状沿程变化较大。图2进一步给出了该河段的高程变化。从图2可以看出，山丘阶地段河道坡降较大，而平原宽谷段河道坡降较小，束窄段与宽谷段相间分布的特点使得该河段坡降呈现出起伏变化的规律。总之，该河段的断面形状和坡降沿程变化较大，宜采用异参离散广义Nash 汇流模型进行河道洪水演算。

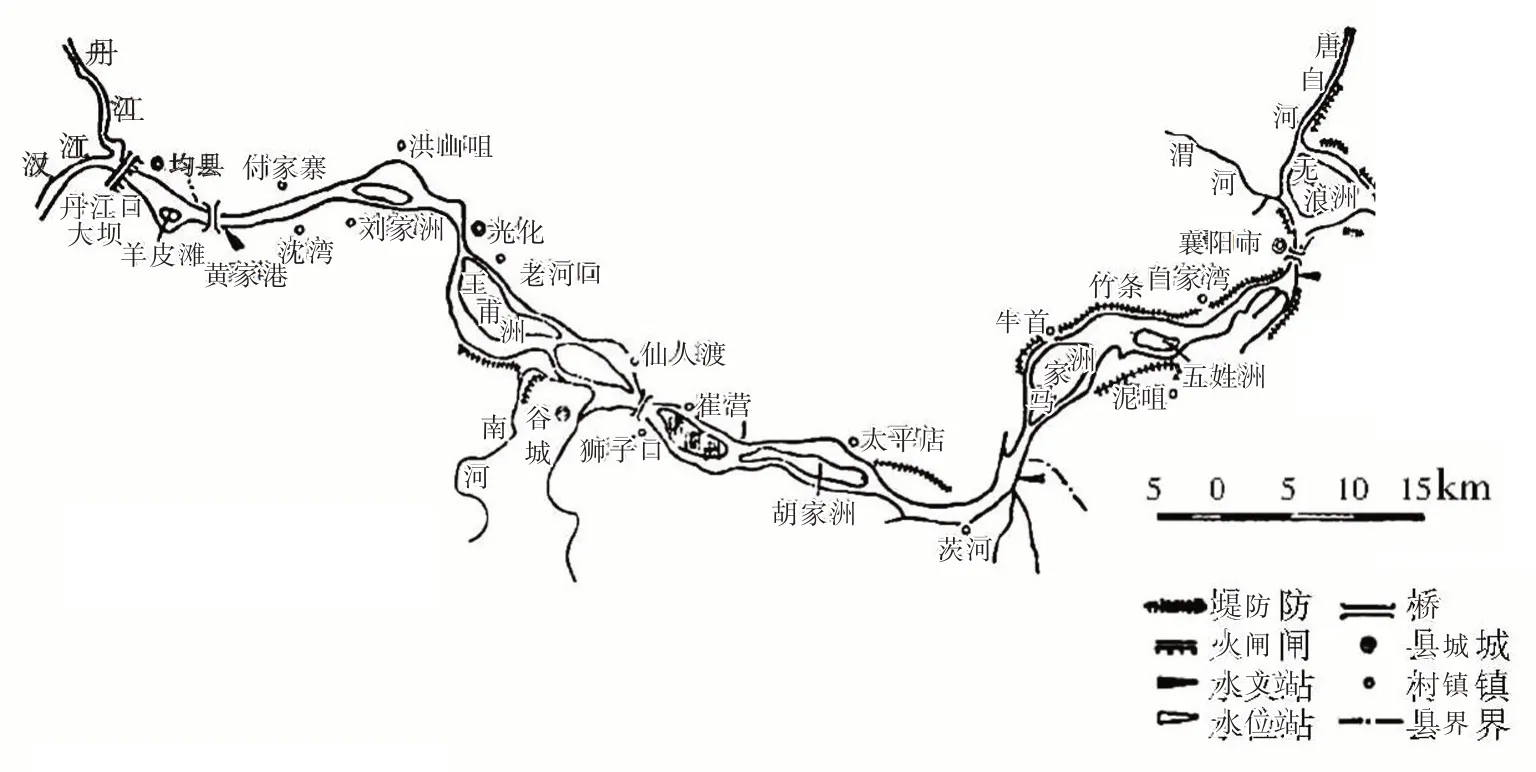
图1 研究河段地理位置及河道形势

根据黄家港、襄阳水文站1970—1989年的洪水摘录资料，选取该河段区间来水所占比重较小的6 场洪水过程（计算时段△t=3 h）进行模拟。为了保持水量平衡，将区间来水按比例均匀分摊到上游断面来水。为了展示异参离散广义Nash 汇流模型的模拟效果，检验其预报能力，选取离散广义Nash 汇流模型进行对比。SCE-UA 算法具有全局收敛性、鲁棒性和通用性等优点，已成为水文模型参数率定常用的优化方法［10］。SCE-UA 算法的参数较多，但大都可以采用已有研究成果的默认值，只有复合形个数需要根据具体问题确定，根据文献［10］的研究，本文复合形个数取为5。以均方根误差最小为目标函数，采用SCE-UA 算法进行模型的参数率定，得到离散广义Nash 汇流模型的参数n=3，K=3.63 h，异参离散广义Nash 汇流模型的参数n=3，K1=1.52 h，K2=9.26 h，K3=1.53 h。参数K 反映了线性水库调蓄性能的差异，离散广义Nash 汇流模型的3 个线性水库具有等效性，实质是对河段的地形差异做了均化处理。而异参离散广义Nash 汇流模型的3 个线性水库中有两个近似相同，而另一个与这两个相差较大，因此能够更加客观地反映地形差异对河槽调蓄性能的影响，理论上可以提高河道洪水的模拟精度。

图2 黄家港-襄阳河段高程变化

两种不同方法的精度评价结果见表1，离散广义Nash 汇流模型的洪峰相对误差基本在8%以内，均值为4.34%，而异参离散广义Nash 汇流模型的洪峰相对误差有所减小，均值为2.59%。洪水过程的模拟结果如图3所示，较之离散广义Nash 汇流模型，异参离散广义Nash 汇流模型均有不同程度的提高，模拟结果与实测过程线也更为接近，尤其是洪峰附近，6 场洪水的平均确定性系数达到0.9766，较离散广义Nash 汇流模型的平均确定性系数0.9672 有一定程度提高。模拟结果表明，较之离散广义Nash 汇流模型，由于考虑了参数K 的空间异质性，使得异参离散广义Nash 汇流模型具有更强的适用性，在河道地形变化较大的河段尤其适用。

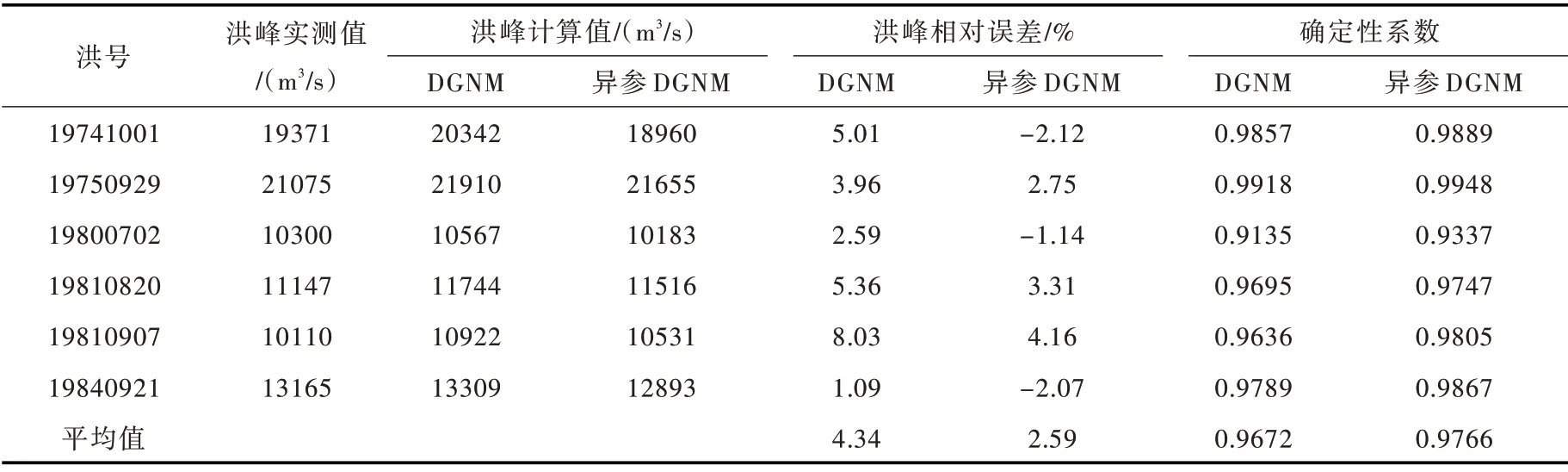
表1 河道洪水演算精度评价结果

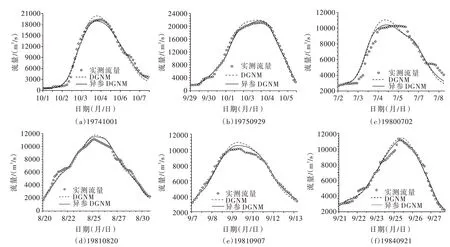
图3 洪水过程模拟结果

5 结论

根据离散广义Nash 汇流模型的概念解析，下游断面的出流是由留在河槽中的“旧水”和上游入流的“新水”共同产生的。其中，“旧水”产生部分可看作是河槽当前蓄水量的退水过程，将各线性水库的当前蓄水量作为瞬时入流，借由瞬时单位线的概念叠加各水库瞬时入流在出口断面的出流过程，即可得到相应的退水过程；“新水”产生部分是上游当前入流及其增量经由各线性水库连续调节而得。离散广义Nash 汇流模型中各水库的调蓄参数K 是相同的，表明该模型主要适用于河道地形变化较小的河段，对于河道地形变化较大的河段，引入异参瞬时单位线及其S 曲线，在离散广义Nash 汇流模型概念解析的基础上，推导得出了异参离散广义Nash 汇流模型，从而丰富了现有广义Nash 汇流理论，扩大了离散广义Nash 汇流模型的适用范围，实例分析也表明，一定程度上还可以提高模型的模拟精度。