响应面优化法在1-MCP 贮藏猕猴桃中的应用

李 劼，王文光，强 磊

（杨凌职业技术学院，陕西杨凌712100）

乙烯是果实成熟的催化剂，典型的呼吸跃变型水果猕猴桃对乙烯更为敏感，贮藏环境中存在微量的乙烯就可以加速猕猴桃后熟衰老。所以控制猕猴桃贮藏环境中的乙烯含量及有效控制采后诱发乙烯代谢过程是延缓猕猴桃果实后熟衰老的有效手段之一。1-MCP（1-methylcyclopropene，1-甲基环丙烯）是乙烯的一种可竞争性抑制剂[1-5]，通过与乙烯受体蛋白结合，调解猕猴桃组织对乙烯的反应[6-9]，从而可以有效地延缓猕猴桃的后熟，延长猕猴桃贮藏期。目前，市场上1-MCP 虽已在猕猴桃贮藏中大量使用，但大多处理方法不规范，尤其在具有较大市场前景的新品种猕猴桃上，使用剂量和处理时间比较随意，导致处理后猕猴桃出现后熟加剧、品质下降及果实腐烂变质等现象。猕猴桃新品种红阳口感独特，具有较大的市场潜力，是目前世界上唯一具有商品价值的红肉型猕猴桃品种[10]。

本研究通过响应面优化法来确定1-MCP 处理红阳猕猴桃的浓度和时间，旨在为延长红阳猕猴桃的贮藏时间提供一定的理论支持。

1 材料和方法

1.1 材料与试剂

供试品种为红阳猕猴桃，采自陕西眉县一个管理较为完善的猕猴桃果园。供试试剂为1-MCP（1-甲基环丙烯），纯度99%，医药级。

1.2 试验方法

1.2.1 1-MCP 处理浓度和处理时间的单因素试验在1-MCP 处理时间为24 h 的条件下，分别用质量浓度为0，0.3，0.6，0.9，1.2，1.5 μg/L 的1-MCP 处理猕猴桃，当乙烯释放量下降趋势放缓时，可以确定1-MCP 适宜的质量浓度范围；在1-MCP 质量浓度为0.6 μg/L 的条件下，分别处理猕猴桃0，12，24，36，48 h，当乙烯释放量变化趋势不明显时，为1-MCP适宜的处理时间范围。

1.2.2 中心组合设计（CCD） 依据对处理浓度和处理时间的单因素试验结果，确定1-MCP 处理的浓度和时间范围，以乙烯释放量为响应值，进行中心组合设计（CCD），对1-MCP 在猕猴桃贮藏中的乙烯抑制效果进行优化。试验因素及水平如表1所示。

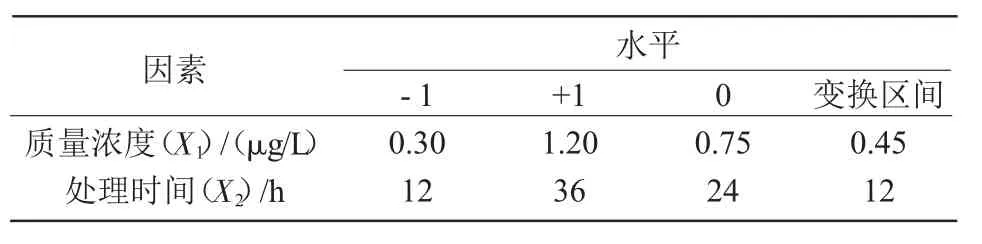
表1 试验因素水平编码

1.2.3 猕猴桃处理方法 选择成熟度一致、果形端正的果实，去除病虫害及机械损伤果。将猕猴桃置于密闭环境中，分别用不同浓度的1-MCP 熏蒸相应的时间，3 次重复，每个重复用猕猴桃10 kg。将处理后的猕猴桃分别装入聚乙烯塑料薄膜袋中，贮藏于温度为（2.0±0.5）℃、相对湿度85%～95%的气调库中，定期采集聚乙烯塑料薄膜袋中的气体进行乙烯测定。

1.2.4 乙烯测定方法[11]采用气相色谱法进行乙烯释放量的测定。用注射器抽取聚乙烯塑料薄膜袋中的气体1 mL，用岛津GC-2014C 型气相色谱仪（配FID 检测器，GDX-502 填充柱，柱温75 ℃，氢气0.7 kg/cm2，氮气1.0 kg/cm2，检测室温度120 ℃）测定乙烯含量。利用峰面积定量测定乙烯释放量。

1.3 数据处理

试验数据采用Design Expert 8.0.6 软件进行处理。

2 结果与分析

2.1 单因素试验结果

2.1.1 1-MCP 处理浓度对乙烯释放量的影响 从图1 可以看出，在1-MCP 处理时间为24 h 的条件下，1-MCP 处理质量浓度为0 时，乙烯释放量最大，达到了0.41 μL/L；随着1-MCP 处理浓度的增加，乙烯释放量呈现出逐渐下降的趋势，当1-MCP 质量浓度达到0.6 μg/L 时，乙烯释放量下降趋势放缓；当1-MCP 质量浓度达到设定的最大值1.5 μg/L时，乙烯释放量下降至0.26 μL/L。

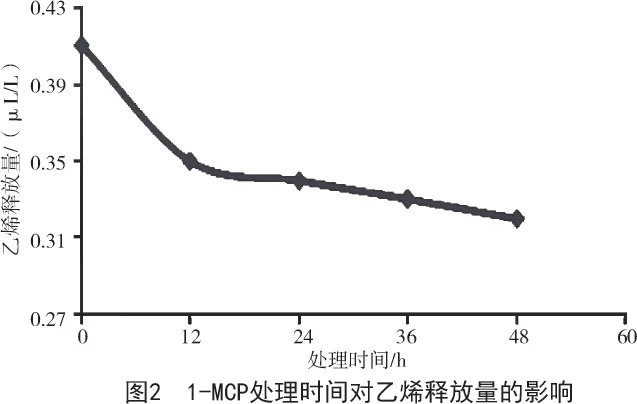
2.1.2 1-MCP 处理时间对乙烯释放量的影响 由图2 可知，在1-MCP 处理质量浓度为0.6 μg/L 条件下，处理0 h 时，乙烯释放量最大，达到了0.41 μL/L；随着1-MCP 处理时间的延长，乙烯释放量呈现出逐渐下降的趋势，当1-MCP 处理12 h 时，乙烯释放量为0.35 μL/L；随着处理时间的延长，乙烯释放量变化趋势不明显，当1-MCP 处理时间达到设定的48 h 时，乙烯释放量下降至0.32 μL/L。

2.2 回归方程的建立及显著性分析

按照中心组合设计（CCD）进行试验，其结果列于表2。

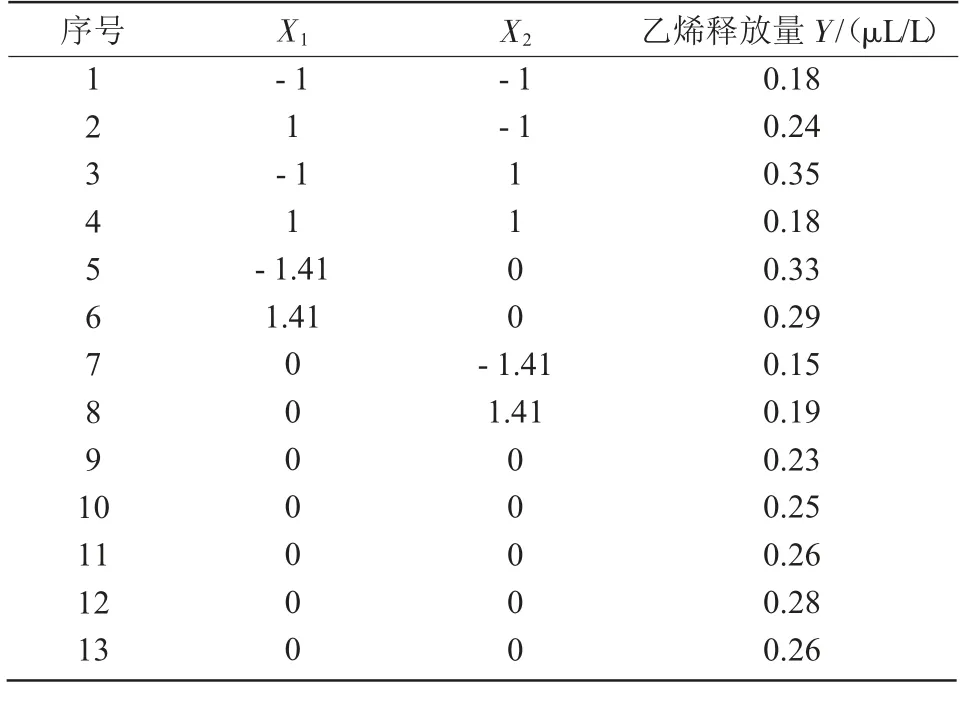
表2 各处理组的得率试验结果

对表2 的试验结果进行统计分析，以5%为置信区间进行显著性水平分析，可以得到如下方程。

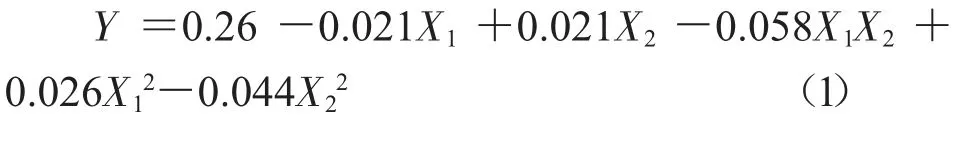
对方程（1）显著性进行统计分析，结果列于表3。

由响应面模型方差分析结果可知（表3），依据回归方程方差显著性要求，当方程模型的显著性为显著、失拟性误差的显著性为不显著时，方程呈现极显著。该方程模型的F 值为27.83，呈现极显著性，失拟性误差的F 值为0.73，呈现出不显著性，所以该方程呈现极显著性。在此回归方程模型中，各因素X1，X2，X1X2，X12，X22的P 值都小于0.05，说明各因素都显著。

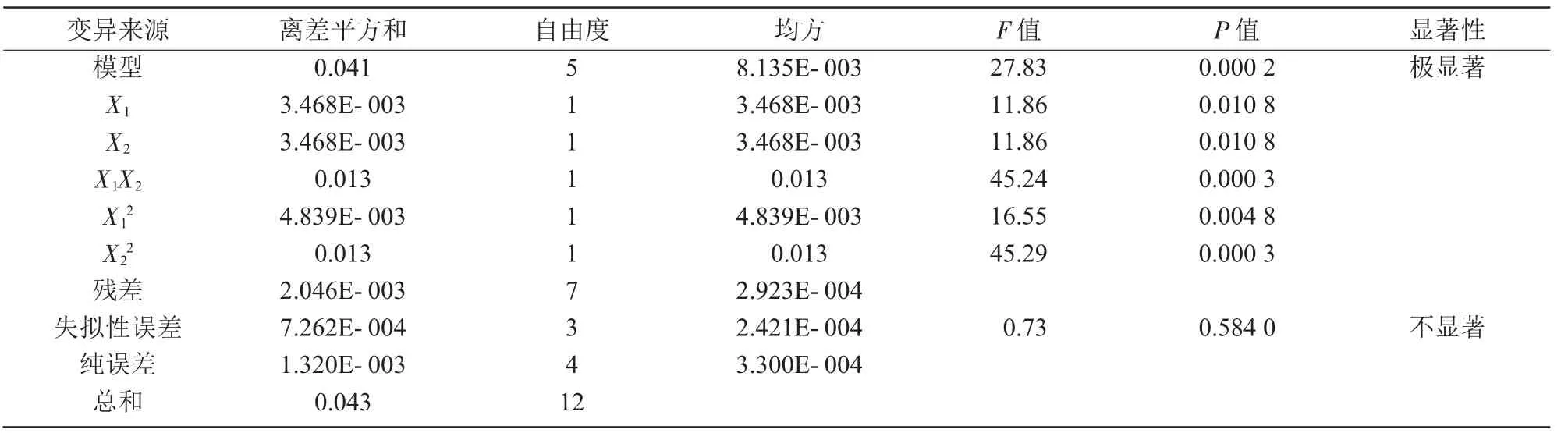
表3 响应面模型方差分析结果

由表4 可知，预测拟合度为0.830 8，校正拟合度为0.917 9，预测拟合度≤校正拟合度，说明模型是合理的。信噪比值大于4 为理想值，本模型的信噪比值为17.123，说明比值理想，本模型方程可以被用来解释设计方案。

表4 数学模型的统计结果

2.3 最佳试验方案的确定

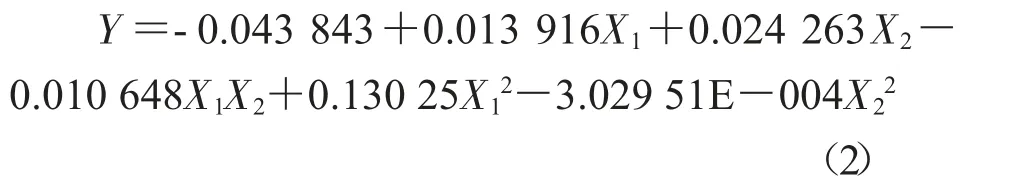
根据二次项中心化，将因素水平代入预测方程（1），可以得到回归方程（2）。从表3 可以看出，1-MCP 质量浓度和处理时间具有极显著的交互作用（P＝0.000 3），达到极显著水平（P＜0.05）。利用Design-expert 8.0.6 软件进行优化处理可知，当1-MCP 质量浓度为0.75 μg/L、处理时间为24 h 时，可以得到最佳的乙烯抑制释放量，此时理论预测的乙烯释放量响应值为0.256 μL/L（图3）。

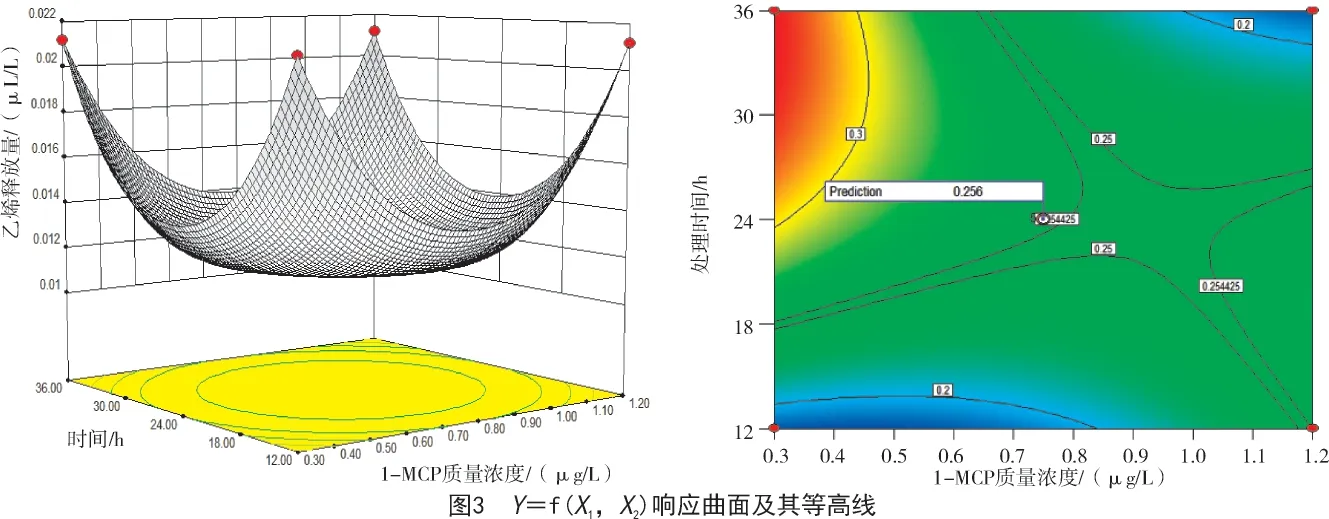
2.4 数学模型预测结果验证

在设定乙烯释放量Y＝0.256 μL/L 的条件下，约束条件取1-MCP 处理浓度和处理时间均在所选范围内（0.3＜X1＜1.2；12＜X2＜36），使乙烯释放量最小，通过数学模型对1-MCP 条件进行优化和预测，在Design-expert 8.0.6 中得出唯一的解决方案，即理论预测值为0.256 μL/L，此时1-MCP 质量浓度为0.75 μg/L，处理时间为24 h。在此条件下试验5 次，实际提取率为0.224 μL/L，与预测结果相吻合。说明利用响应面分析法优化1-MCP 是可行的。

3 结论

本研究采用中心组合设计（CCD）法对1-MCP在猕猴桃乙烯释放量进行预测，建立了乙烯释放量与1-MCP 浓度、处理时间之间的回归方程模型，用回归方程模型对乙烯释放量进行预测，确定了最佳的1-MCP 浓度和处理时间。当1-MCP 质量浓度为0.75 μg/L、处理时间为24 h 时，乙烯释放量达到了较低的释放水平0.224 μL/L。