Efficient solver for time-dependent Schrödinger equation with interaction between atoms and strong laser field∗

Sheng-Peng Zhou(周胜鹏), Ai-Hua Liu(刘爱华), Fang Liu(刘芳),Chun-Cheng Wang(王春成), and Da-Jun Ding(丁大军),†

1Institute of Atomic and Molecular Physics,Jilin University,Changchun 130012,China

2Jilin Provincial Key Laboratory of Applied Atomic and Molecular Spectroscopy(Jilin University),Changchun 130012,China

3School of Mathematics and Statistics,Changchun University of Technology,Changchun 130012,China

Keywords: time-dependent Schrödinger equation,Strong laser fields,Parallel numerical solver

1. Introduction

Theoretical simulation plays an important role in understanding of the interaction of atoms or molecules with a strong laser field. There are various methods of simulating the strong-field physical processes, such as the simple-man model,[1]strong-field approximation (SFA),[2,3]classicaltrajectory Monte Carlo simulation (CTMC),[4]quantumtrajectory Monte Carlo (QTMC),[5,6]etc. While the most accurate theoretical method of obtaining the complete information is to solve the time-dependent Schrödinger equation(TDSE).However, solving the three-dimensional(3D)TDSE for simulating such laser interactions with atoms becomes a challenge because,with the development of laser technology,the laser field intensity can be much higher than the overbarrier ionization region of atoms or molecules. Although many efforts have been made in the past few decades[7-14]to tackle this challenging problem, it still needs more efficient numerical methods,parallel to adapting to the development of computer technology.

Several efficient parallel methods of solving the 3D TDSE[15-18]have been developed, mainly based on direct TDSE solutions in Cartesian coordinates. Considering the atomic spherical symmetry,it should be better to choose spherical coordinates in computation but this is difficult because,in general, the methods with using the basis set expansion techniques in spherical coordinates are not suitable for parallel calculation.[15]To solve this problem, Patchkovskii et al.have proposed a parallel method,[18]and achieved the spatial derivatives of the radial coordinate by using the finitedifference method (FDM), which leads to an increase in the grids for the larger sized problem,[17]and finally significantly increasing the amount of computation in the case of higher accuracy.[19]Guan et al. solved TDSE of two-electron quantum system in spherical coordinates efficiently based on the finite-element(FE)discrete-variable-representation(DVR)and Short-Iteration-Lanczos(SIL)propagator,[20]because the FE-DVR can offer higher computing accuracy[21]and make the Hamiltonian matrix very sparse, whose effects are similar to those provided by the B-spline[22,23]and sine-DVR,[24]and the efficiency of the wave function evolution strongly relies on the sparsity of the Hamiltonian matrix for the SIL propagator.[25]The most ideal structure of the Hamiltonian matrix is expected to have diagonal or similarly sparse elements for the SIL propagator.

In this work, we develop a parallel numerical method of solving TDSE in spherical coordinates for simulating linearly polarized laser interacting with single active electron (SAE)atoms. First,a sparse Hamiltonian matrix is constructed based on the FE-DVR and spherical harmonics functions. Second,ideal sub-matrices are separated out from the Hamiltonian matrix for the SIL propagator,[26,27]which is based on the real space product formula (RSPF). This combination guarantees efficient parallel computing for the simulation of real physical problems. We then apply this method to the efficient calculation of atomic high harmonic generation(HHG).Atomic units are used throughout this paper unless otherwise indicated.

2. Method

To simulate the interaction of atoms with linear polarized laser fields,[24,28]the TDSE for the full wave function can be expressed as follows:

with the potential term V(r)=-1/r(atom hydrogen)and the laser-matter interaction term defined as

The length gauge is adopted in this computation. Thus, the Schrödinger equation for the reduced wave functions can be rewritten as follows:

with

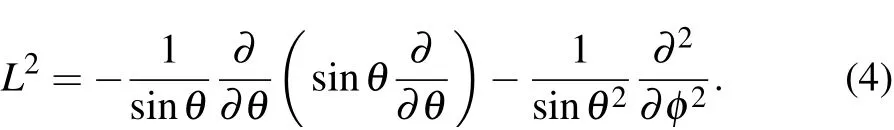
To solve Eq.(3),the reduced wave function ψ(r,t)is expanded into a series of spherical harmonics Ylm(θ,φ)and radial functions φlm(r,t),

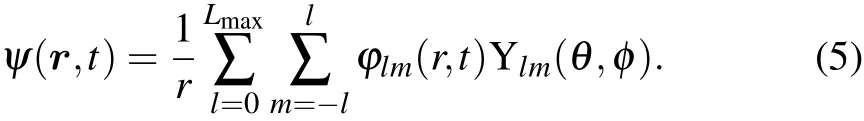
For a linear laser field,none of photons have angular momentum,so that all calculations can be done with m=0 if the initial atomic state has a zero magnetic quantum number. Thus,equation(5)is reduced as follows:

The partial waves can be further discretized as φl(r,t) =where χk(r) is FE-DVR base. Two vectors are set to be X(r) = (χ1(r),χ2(r),...,χk(r)) and Cl(t) =(cl1(t),cl2(t),...,clk(t)). Substituting Eq. (6) into Eq. (3), and separating the time-dependent parts from time-independent parts of the Hamiltonian matrix, the corresponding diagonal matrix element and off-diagonal matrix element are given by[24]

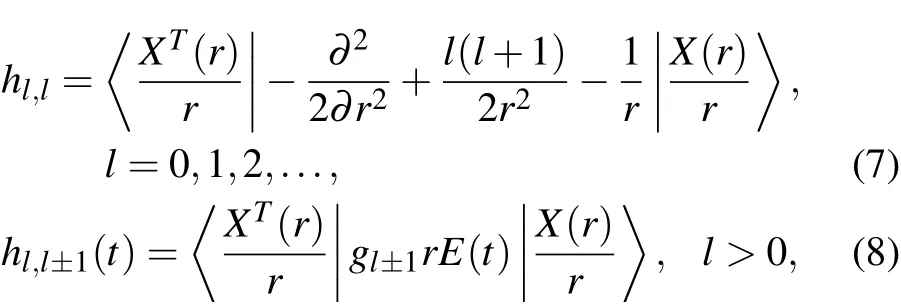
where glis

The Hamiltonian matrix is symmetrically tridiagonal,as indicated below.

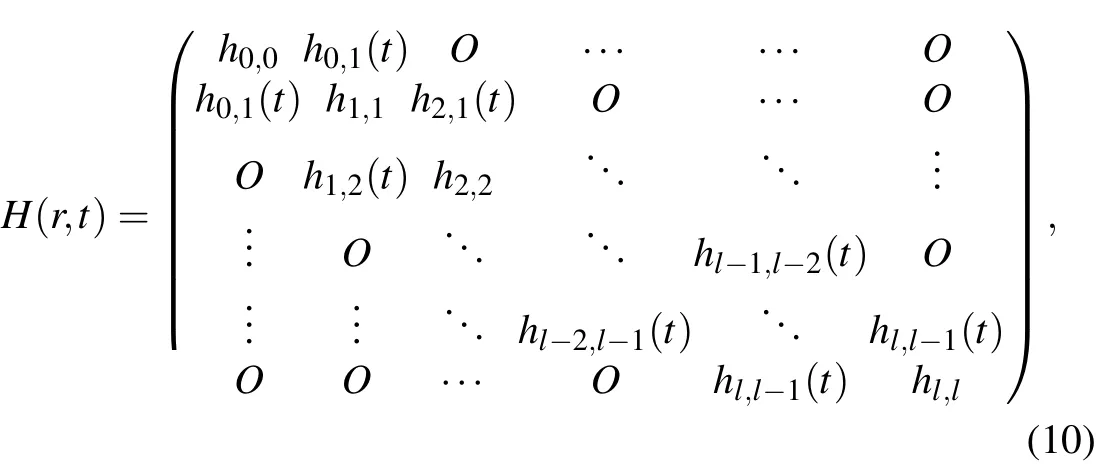
where O is the zero matrix.According to the RSPF,H(r,t)can be divided into two matrices A and B(t),

Here,B(t)is not a diagonal matrix and can be reshaped further.After setting

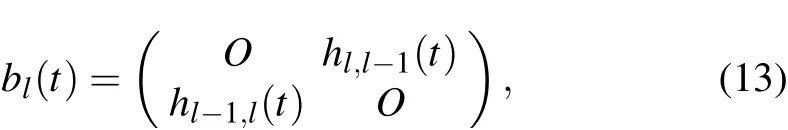
B(t) can be decomposed into two block diagonal matrices as follows:

Using Lie-Trotter-Suzuki product formula(LTSPF),[29,30]the propagation scheme can be expressed as

As shown in Eqs.(11)and(14),the matrices A,Beven(t),and Bodd(t)are block-diagonal matrices.The sub-matrices in these three matrices act independently on the corresponding partial waves. Thus, the parallelization of propagation scheme can be realized programmatically which can be used very well to solve TDSE as shown in a two-electron case.[31]From a concrete realization of the propagation exp(-iδtA), for each hl,lin matrix A,

And for each bl(t)in Boddand Beven,

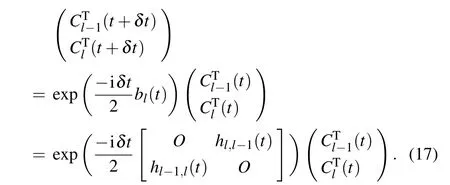
According to the space division scheme of FE-DVR,[32]the radial coordinate of the interval[0,rmax]is divided into nefinite elements. In each FE (i.e., in [ri,ri+1]), nglocal DVR bases χi,mare constructed based on the generalized Gauss-Lobatto points rimand weights wim. In the numerical computation,χk(r)=χi,m(r). So,the partial waves can be expressed. The boundary conditions that the wave function vanishes at r11=0 and rneng=rmaxare imposed by deleting the first and last functions χ1,1and χne,ng. There are nbasis=neng-ng-1 basis functions in use.

According to the characteristics of the FE-DVR bases,the potential-energy matrix and the matrix of any other local operator turn out to be diagonal with regard to the elements i and local DVR basis indices m;i.e.,

While for the kinetic-energy representation, the matrix is shown in a diagonal overlapping block structure as follows:[33]

Therefore, the elements of matrix hl,lin Eq. (11) can be expressed as

Since it is represented based on FE-DVR,the structure of Eq.(8)is also like the potential-energy matrix,

For hl,l-1(t)=hl-1,l(t),bl(t)in B(t)is expanded into a sparse symmetric matrix and expressed as

Obviously, bl(t) is an ideal matrix for the SIL propagator in the perspective of efficiency. The number of nonzero elements in bl(t) is equal to the size of diagonal element of bl(t). This suggests that the ideal method of propagating partial waves in Eq.(17)is the SIL propagator.For the SIL propagator,an orthonormal Krylov subspace is constructed through recursive relations for each time step,

where H=bl(t),αjand βjare expressed as

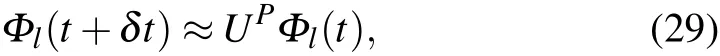
and

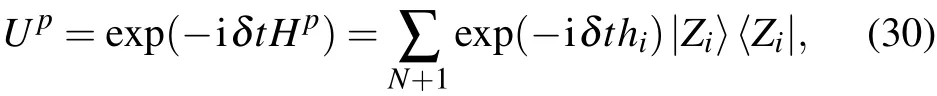
where|Zi〉and hiare the corresponding eigenvalue and eigenvector of Hp. Because it is mainly affected by the operator of bl(t) times the vector pjin Krylov subspace PN, the calculation scale of the SIL operator is proportional to

It is noted that for propagating the partial waves in Eq.(16)in the SIL frame,the calculation scale is proportional to

because the number of nonzero elements in hl,lis ne(ngng-1)-1. Comparing with the ideal matrix like bl(t),the calculation scale of the SIL propagator for hl,lincreases ngtimes approximately when neis large. It indicates that the SIL propagator is not a good choice in this case. To overcome this difficulty,in the numerical calculation we decompose the matrix hl,linto smaller sub-blocks, and then the sub-blocks are diagonalized as given in Ref.[26]. Compared with diagonalizing the whole matrix of hl,ldirectly,this method can greatly reduce the amount of computation. Meanwhile,the matrix hl,lis time-independent,and the operations of decomposition and diagonalization of hl,lonly need performing once before timedependent propagating, which further reduces the amount of computation.

3. Application to numerical simulation of atomic HHG

In the following, we mainly apply the present solver to the 3D TDSE of HHG from atomic hydrogen in a strong laser field. The parallel program is implemented in the FORTRAN language with openMP. The calculations are carried out on a workstation with two processors(Intel Xeon CPU,E5-2696v4,22 cores, 2.20 GHz). In the calculations, the laser field is 800 nm in wavelength and 1.0×1014W/cm2in power and has an envelope of cos2(πt/nT),where T is the time of an optical cycle,and n=10,the full width of half maximum of the laser pulse is about 13.34 fs.The initial state of hydrogen atom is 1 s. The parameter of time is set to be Ttotal=1200.0 a.u.and Δt=0.01 a.u. The radial space region is in[0,200.0]a.u.

As is well known,the reliability of the solver is very important for simulating the real physical process of atoms interacted with strong laser fields. Figure 1 shows the HHG obtained from the present program, compared with the result of well-established SCID-TDSE,[18]which is a program of time-dependent solution of 1-electron atomic Schrödinger equation in a strong laser field,and performed as well as LZHDICP.[24]The high-harmonic spectrum of SCID-TDSE is calculated from the Fourier transform of the real part of the expectation value of the dipole response. The high harmonic spectrum of our result is calculated from the Fourier transform of the real part of the expectation value of the time-dependent induced dipole acceleration response.[34]In this calculation,the parameters are chosen to be ng=6,ne=200,Lmax=100,and N=3. For obtaining a convergent result with the program SCID-TDSE, the parameters are Δr =0.3 a.u., Lmax=100,and Δt =0.0005 a.u. The consistency between the two re-sults indicates that our solver is reliable. The visible difference between the two high-harmonic spectra in the high energy region is due to the fact that the precision of HHG with high energy obtained from the dipole response is not enough.It is noted that our program is several times faster than the SCID-TDSE when the two programs run on the same workstation with 32 threads,which is in line with expectations for the reason why the FDM of the program SCID-TDSE requires smaller time steps to ensure the convergence.[35]The present solver can also be used to obtain the HHG of Ar atom in the same laser field with a model potential.[36]There is a need for more FEs(ne=320)in the radial space for the steeper potential of Ar atom near nucleus. The power of the HHG of Ar atom as shown in Fig. 1(b) is greater than that of hydrogen atom for the larger tunnel rate of 3p state with higher angular momentum.[37]

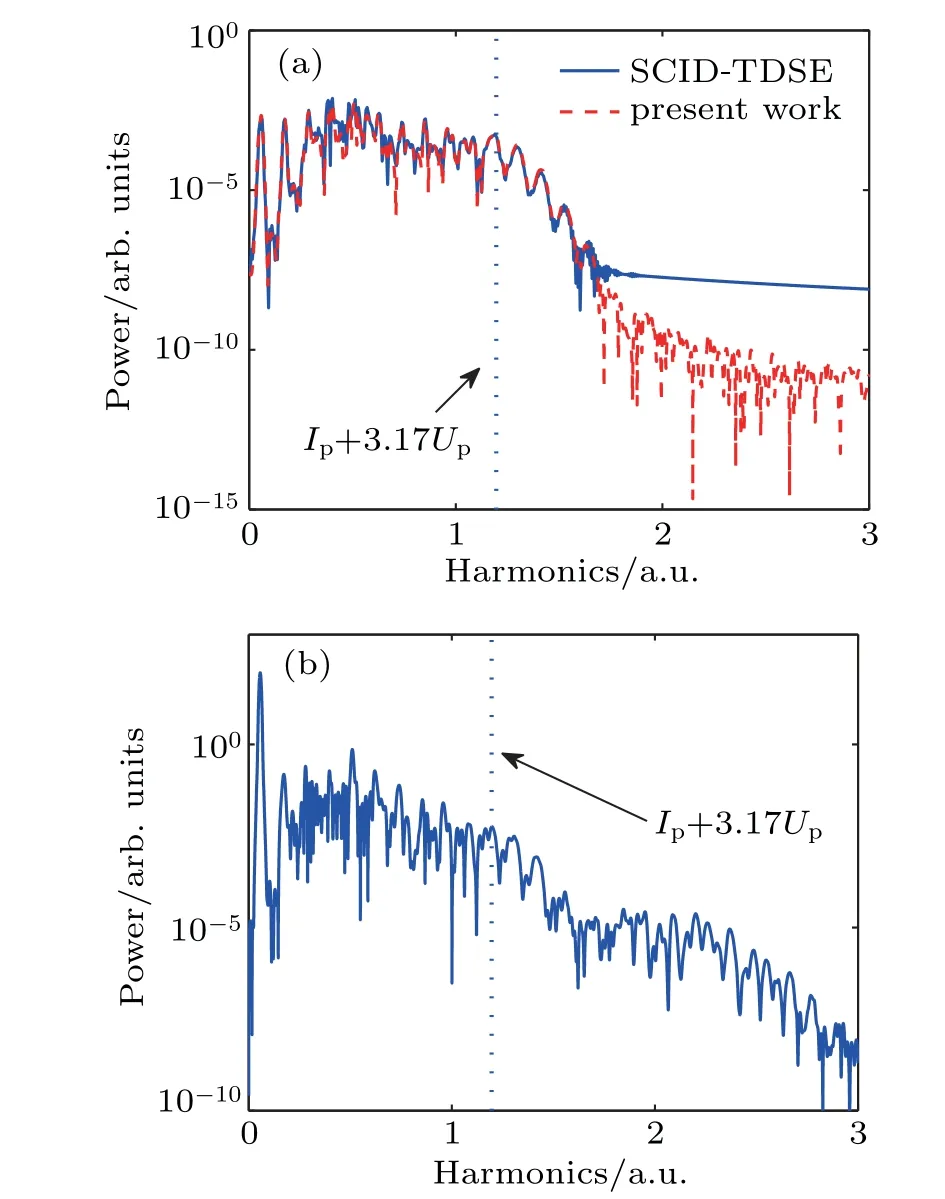
Fig.1. (a)Comparison between HHGs obtained from our program and the program SCID-TDSE,[18] (b)HHG of Ar atom driven by intense laser field(800 nm and 1.0×1014 W/cm2). Up represents ponderomotive potential,and Ip denotes ionization energy of hydrogen atom.Cut-off position of HHG is marked with blue dashed line Ip+3.17Up.

The precision of the present solver is mainly affected by the discretization of space and time. The precision of the discretization of space based on the FE-DVR has been discussed in detail in Ref. [27]. The inappropriate values of neand ngwill increase the error of calculation as done by underfitting or overfitting. The error caused by the discretization of time has two main sources, one is from the operator splitting of exponential function in Eq. (15)which is proportional to Δt3, and the other is from the propagation based on the SIL propagator in Eqs.(29)and(30)that relies on the order of the Krylov subspace,and expressed as

To investigate the total error of the solver, the HHG of the calculations with different orders of the Krylov subspace is shown in Fig.2(a). Figure 2(b)shows the comparison among the phases of HHG which are more sensitive to the accurate.The calculations are carried out with 32 threads. The parameters are ng=6,ne=200,and Lmax=200. Figures 2(a)and 2(b)show clearly that the results are convergent when N ≥3,since the precision of the SIL propagator is consistent with the precision of the operator splitting of exponential function when N=3 according to Eq.(31).

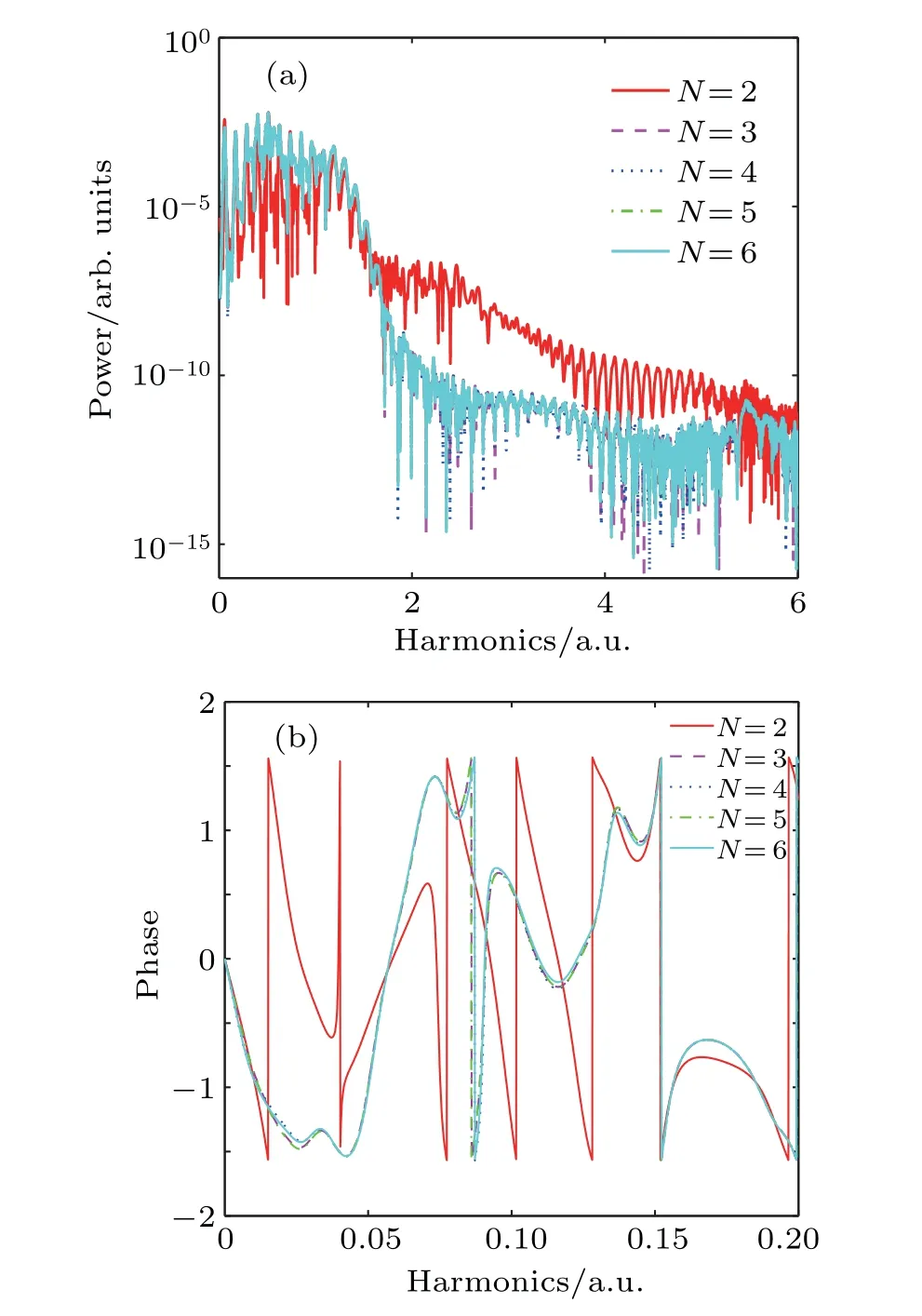
Fig. 2. Plots of (a) power and (b) phase versus harmonics of HHG of hydrogen atom driven by intense laser field (800 nm and 1.0×1014 W/cm2),obtained by using Krylov subspace with different orders.

It is noticeable that splitting out the centrifugal potential from the SIL propagator in our scheme is also one of the reasons of fast convergence with small order of Krylov subspace,which has the same result as that of Ref.[35].The requirement for the small order of Krylov subspace means that a lot of time consumption of calculation can be saved according to Eq.(31).It is known that the requirement of accuracy increases with the increase of the laser intensity. So we give out the phase of HHG of Hydrogen atom in the laser field with its intensity up to 1.0×1015W/cm2as shown in Fig. 3(a). It is obvious that three orders of Krylov subspace can meet the accuracy requirement. Three orders of Krylov subspace can also meet the accuracy requirement for Ar atom in an intense laser field as shown in Fig.3(b).

Fig.3. Plots of(a)phase of HHG of hydrogen in intense laser field(800 nm and 1.0×1015 W/cm2), (b)plots of a haze of HHG of Ar atom in intense laser field(800 nm and 1.0×1014 W/cm2),obtained by using Krylov subspace with different orders.

For a solver,propagating the wave packet efficiently with a dense matrix such as hl,lis a tricky problem. The propagator for the relatively dense matrix hl,lin our solver is not the SIL propagator, its time consumption does not dependent on the order of the Krylov subspace. It can be seen in Fig.4(a)that the total time consumption of calculations varies with the order of the Krylov subspace as a linear function of N, specifically f(N)=a×N+b. Thus,b=42.27(seconds)is the time consumption relating to the matrix hl,l,and a×N(a=11.63(seconds)) is the time consumption for the matrix bl(t). If the SIL propagator is adopted for the matrix hl,l, then based on Eqs. (31) and (32) it can be deduced that the time consumption can be given as f(N)≈(a/2)×ng×N. For the cases of N=3 and ng=6,the time consumption for the matrix hl,lis about 104.67 seconds,which is more time consuming than that of our method for the matrix hl,l. This can make a significant statement that the propagation for the matrix hl,lin our solver is high efficient.

Finally, the time consumption varying with the number of threads in the calculations of HHG is studied as shown in Fig. 4(b) with the parameters being Lmax= 200, ne= 200,and ng=6. This figure shows almost linearly scaling up to 32 threads,which indicates that the parallelism of the present solver is valid.

4. Conclusions

We have described an efficient parallel solver of TDSE simulating the interaction of atoms with a linearly polarized laser field. In this solver, the electronic wave function is expanded in terms of FE-DVR and the spherical harmonics. According to the RSPF, we implement the program in parallel,and improve the efficiency by separating out the ideal sparse sub-matrices from the Hamiltonian matrix for the SIL propagator. By decomposing and diagonalizing the sub-matrices including kinetic operator representation before time-dependent propagating, we can further improve the computational efficiency. Comparing with the split-Lanczos propagator,[35]the efficiency of our solver is high because the SIL propagator is applied to the sparser matrix bl(t) instead of the matrices including kinetic operator. We use the solver to simulate HHG of atomic hydrogen in an intense laser field. The results show that the solver of TDSE has less time consumption and better parallel efficiency. In addition, it is expected that the present solver combined with the Wigner rotation technique should be utilized for simulating the interaction of atoms with circularly polarized intense laser field. For the TDSE for a two-electron system in spherical coordinates,a lot of block sub-matrices exist in the Hamiltonian matrix as a result of transition limits or parity conservation,[20,38,39]our adopted method of separating and constructing block diagonal matrices may also increase the efficiency of solving the TDSE of a two-electron system interaction with an intense laser field.

Acknowledgment

We thank the High Performance Computing Center of Jilin University for the supercomputer time.