汽车悬置系统垂向耦合振动特性分析

马骏 韩加蓬 李煜

山东理工大学交通与车辆工程学院 山东省淄博市 255049

1 引言

研究表明，驾驶员及乘客如果处于低频率振动条件下较长时间时，易出现疲劳、反应迟缓、协调性差、注意力不集中等影响正常驾驶的不良状况，高强度的振动还会对乘员的腰部、脊柱、胸腔以及颈部等造成损伤，严重影响工作效率及身体健康[1-2]。

汽车行驶过程中，路面不平度产生的激励使轮胎发生振动，并通过悬架、车身、座椅传递给人体，引起振动使人体感觉不适。汽车的振动系统主要可分为三大隔振环节：轮胎、悬架及座椅[3]。本文通过搭建三自由度四分之一“轮胎——车身——座椅人体”垂向振动力学模型，采用模态分析法，分析模型的固有特性、振动传递特性以及输入响应特性，得到了人体最敏感的频率范围。

2 被动汽车悬架动力学模型

忽略弹簧及座椅底板等部件的变形，将弹簧视为线性化元件，轮胎视为考虑刚度和阻尼的质量单元，仅考虑轮胎、车身和座椅的垂向运动，建立如图1所示的三自由度四分之一车隔振系统模型。

图1中， mt、 mb、mc分别为悬架簧下质量、车身质量和座椅人体质量， K1、 C1分别为轮胎的等效刚度和等效阻尼系数， K2、C2分别为汽车半主动悬架的刚度和阻尼系数，K3、 C3分别为座椅悬架的刚度和阻尼系数，q为路面不平度位移输入， Zt、 Zb、 Zc分别为车轮垂向位移、车身垂向位移和座椅人体垂向位移。

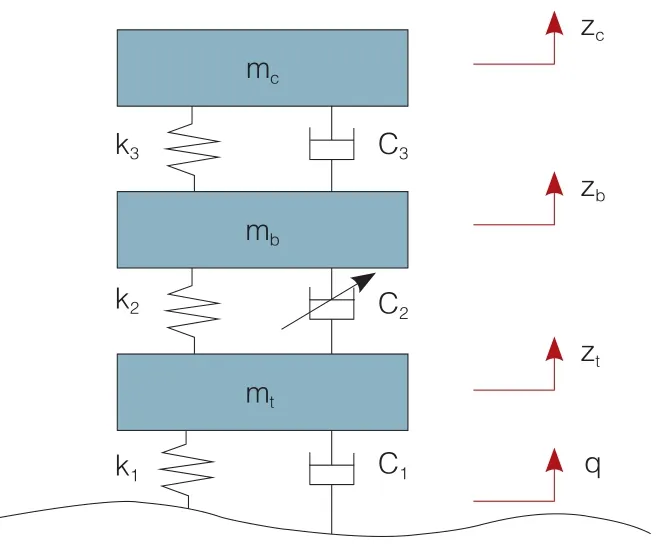
图1 汽车悬置系统三自由度1/4车体模型

根据牛顿第二定律，建立图1的动力学方程为

状态变量的物理意义分别为： x1为座椅人体的速度， x2为座椅悬架的动挠度， x3为车身的速度， x4为车身悬架的动挠度， x5为车轮的速度，6x为轮胎的动变形。选取输出变量

输出变量的物理意义分别为：1y为座椅人体加速度，2y、为座椅悬架动挠度，3y、为车身悬架动挠度， 为轮胎动变形。

悬架系统的状态空间[4]表达式

结合上述所建立的三自由度汽车半主动悬架系统模型，建立半主动悬架系统状态空间方程

其中，u为半主动悬架系统车身悬架阻尼力，ω为零均值的白噪声。

3 被动汽车悬架系统特性分析

3.1 系统固有特性

系统固有特性包括固有频率及主模态[5]。系统的固有频率，可由系统无阻尼自由振动微分方程得到，即

系统三个固有圆频率 ，可得

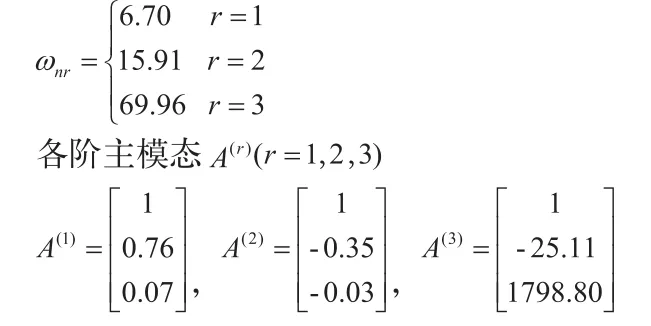
3.2 系统振动传递特性

由输入、输出量 )(tz 与 )(tq 的拉普拉斯变换Z(ω)与Q(ω)的比值[6]，可以求出系统的频率响应函数 H (jω )zc～q

车身位移和座椅位移对路面位移q的频率响应函数：

3.3 座椅人体加速度、悬架弹簧动挠度和车轮相对动载的幅频特性

图2 系统车轮、车身及座椅人体对简谐输入激励的幅频特性曲线

车轮相对动载 GFd/对·q的幅频特性

3.4 路面输入响应

分别采用脉冲激励和正弦波激励，对系统响应进行仿真[7]，仿真框图如图4所示。

脉冲激励响应开始及结束时间分别为4s和6s，仿真结果如图5所示。

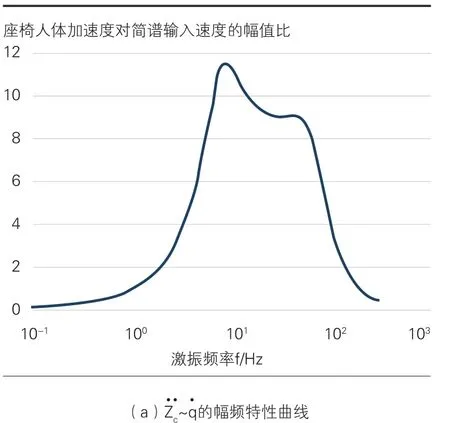
图3 座椅人体加速度、悬架弹簧动挠度和车轮相对动载对·q的幅频特性曲线

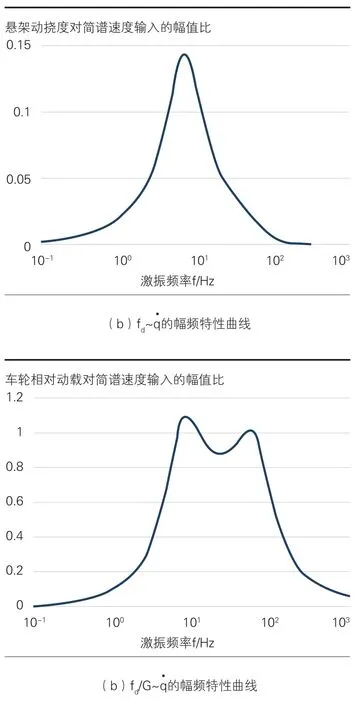
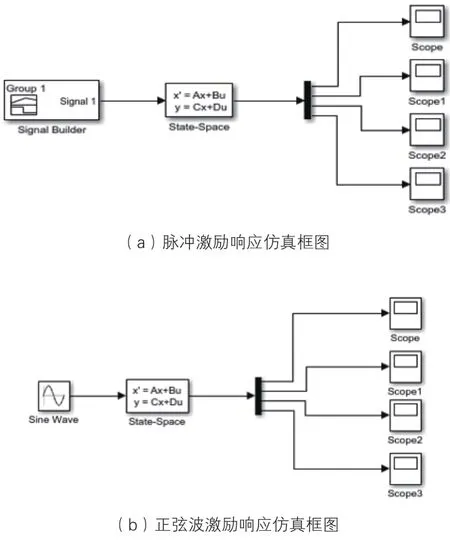
图4 仿真框图

正弦激励幅值取1m，频率取1rad/s ，仿真结果如图6所示。

4 结语

本文考虑车轮阻尼及座椅人体的垂向振动，建立了三自由度四分之一车辆被动悬架和半主动悬架隔振系统简化模型。通过简化模型建立的微分方程，分析了系统的固有频率和主振型，采用拉普拉斯变换法求得座椅人体位移对路面激励的传递特性，并分别求得座椅人体加速度、悬架弹簧动挠度和车轮相对动载对路面速度激励的幅频特性。以建立路面白噪声激励为基础，采用状态空间法，分别分析了在脉冲激励、正弦波激励下的座椅人体加速度、座椅悬架动挠度、车身悬架动挠度和轮胎动变形的响应。同时，通过上述分析可以看出，人体最敏感的频率范围为4～8Hz，上述悬架的低频固有频率为6.7Hz，在此激振频率作用下将产生严重的共振现象，极大的响应司乘人员的乘坐体验。

图5 脉冲激励响应

图6 正弦波激励响应