相对性原理与惯性系的时空变换
2019-08-15戴又善倪杰
戴又善 ,倪杰
(1.浙江大学城市学院,浙江杭州310015;2.浙江大学物理系,浙江杭州310027)
爱因斯坦在1905年提出了狭义相对论[1-2](以下简称相对论),100多年来,相对论经受了大量实验的检验,已成为近代物理的理论基础。传统相对论是建立在相对性原理和光速不变原理的基础上。传统相对论告诉我们,惯性系之间的时空变换为洛伦兹变换[3],但在各种相对论教科书和文献中,推导洛伦兹变换公式通常需要基于一些基本假设,如时空为线性变换的假设以及光速不变的假设[4-5];在一些教科书和文献中,常用牛顿惯性定律以及惯性系的时空平移不变性来证明惯性系的时空变换必须为线性变换[6-7]。当然,系统的能量守恒和动量守恒来源于时空的平移不变性。尽管这些物理定律和假设(如牛顿惯性定律,动量守恒和能量守恒定律,以及光速不变假设)可以与相对性原理相自洽,但其本质上均独立于相对性原理,对于洛伦兹变换公式的推导只是充分条件而不一定是必要条件。如果不依赖这些额外假设,仅仅由相对性原理能否推导出惯性系之间的时空变换公式是一个值得探讨的问题。
众所周知,在相对论运动学中依据光速不变假设可以推导出洛伦兹变换公式,而在相对论动力学中利用洛伦兹变换公式以及动量守恒和能量守恒定律可以得到质速关系和质能关系E=mc2[8]。在一些场论的教科书中则是通过构造单粒子的拉氏量来建立相对论力学[9-10],但拉氏量的构造需要以物理对称性作为理论基础,显然上述的拉氏量具有洛伦兹变换和时空平移变换下的不变性。拉氏量中的洛伦兹对称性和引进极限速度c的物理依据是光速不变假设,而时空平移不变性则意味着动量守恒和能量守恒。因而通常认为传统相对论理论必须是建立在光速不变假设和动量、能量守恒定律之上的。
光速不变假设是否为相对论的必要条件值得质疑,光速不变的实质是理论上将光子作为零静质量粒子以及引进了光速c作为极限速度。由于相对论是普遍适用的基础理论,不应建立在特殊物质的特性之上。即使不依赖光、不依赖静质量为零的粒子,相对论依然应当成立。笔者分别在文献[11]中通过讨论一个完全非弹性碰撞过程、在文献[12]中通过讨论一个两体弹性散射过程、在文献[13]中通过讨论粒子的两体衰变过程,均证明了只需依据相对性原理和动量、能量守恒定律,就可以建立相对论理论;也可以不依赖静质量为零的粒子来引进极限速度vm。说明光速不变假设只是建立相对论的一个充分而非必要条件。
虽然通常利用动量守恒和能量守恒定律来推导相对论质速关系和质能关系,但对于动量守恒和能量守恒定律是否为建立相对论的必要条件同样存有疑问。质能关系和质速关系应该是粒子的基本物理属性,而一个自由粒子本身所具有的质能关系和质速关系显然与相互作用过程无关,也与外部是否存在光子无关,因而粒子的质能关系和质速关系本质上并不依赖于光速不变假设和相互作用守恒定律。
本文仅依据相对性原理,就可证明惯性系之间的时空变换必为线性变换。说明惯性系的时空线性变换特性是相对性原理的直接推论。同时,建立了时空线性变换系数与粒子无量纲质速关系之间的普遍联系。因此,只要知道了质速关系就能完全确定时空变换公式。本文的推导无须讨论相互作用过程,因而也不再依赖动量守恒和能量守恒定律。依据相对性原理最终推导了惯性系之间时空变换的广义洛伦兹变换公式。需要说明的是,在笔者以前发表的相对论研究论文中,均假设了时空变换是线性变换[11-14],因而本文也是依据相对性原理提供了对于惯性系时空变换必须是线性变换的一个补充证明。
1 时空变换公式与粒子质速关系
下文仅限讨论存在静止参考系的粒子,即允许粒子静止在参考系中,因此可以定义这类粒子具有非零的静质量m0>0。当粒子运动速度为v时,粒子的动量为p=p(v)。考虑单位矢量令函数m()=|,由此可得 p(v)=m()。因为和p都是三维空间矢量,在空间反演下变号:则 有m(-)=m(),由此可知,要求 m()=m,其中v=|v|。而能量在空间反演下不变,E()=E。则粒子动量和能量的一般形式分别为

其中m=m(v2)是粒子运动速度的函数,且具有质量的量纲,称为动质量,其函数关系通常称为质速关系。粒子的静质量为

依据相对性原理,所有惯性系都是等价的,则在不同惯性系中要求动量和能量对于粒子速度的依赖关系具有相同的函数形式,即在任意惯性系S′中,当粒子的速度为v'时,其动量和能量可表示为
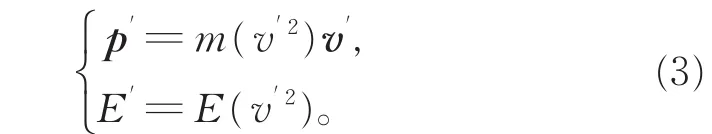
设一相对于惯性系S沿X方向以速度V运动的惯性系 S′,见图 1。
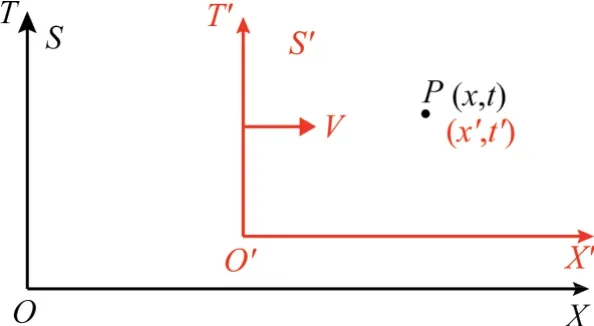
图1 不同惯性系的时空变换Fig.1 Transformation of space-time in different inertial reference frames
相应地,一般时空变换关系为
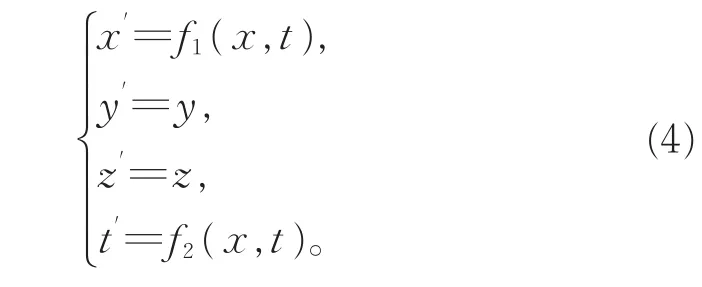
对式(4)求导可得
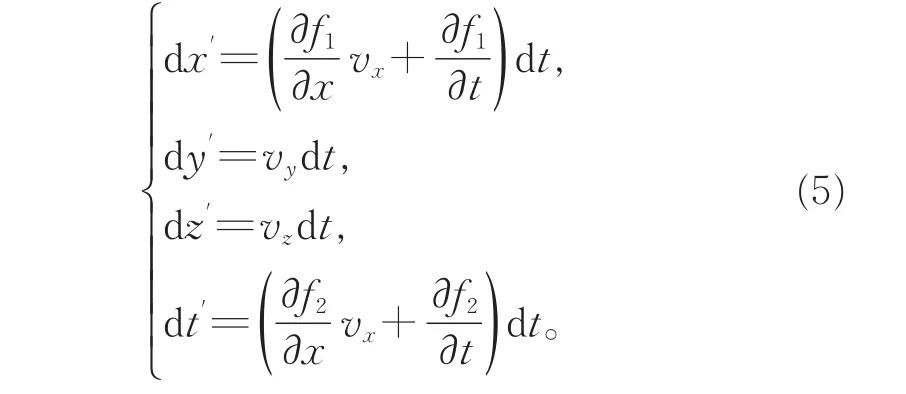
由此可求得一般的速度变换关系为

由于S′系和S系在Y方向无相对运动,因此,在2个参考系中粒子动量的Y方向分量保持不变:py=p′
y(严格证明见附录A)[15]。需要强调的是,这并非相互作用过程中的动量守恒要求,而是动量本身在参考系变换下所具有的线性变换特性。由式(6)可得

因而有
当一粒子静止在S′系中即v'=[0,0,0],在S系中 该 粒 子 的 速 度 为 v=[V,0,0],即 有 v′x=0,vx=V,v′2=0,v2=V2。 由 式 (6)第 1 式 可 得 0=即有

由式(8)则有

若考虑一粒子静止在S系中,即v=[0,0,0],则该粒子相对于S′系的运动速度为v'=[-V,0,0],即有 vx=0,v′
x=-V,v2=0,v′2=V2。代入式(8)后可化为
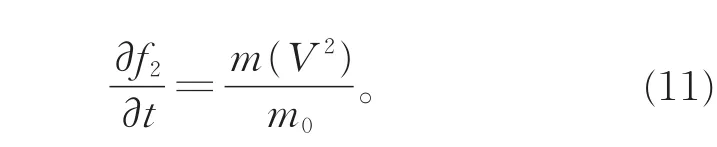
代入式(10),即有

需要说明的是,虽然上述关系是在粒子运动速度的某种特例情况下推得的,但由于f1(x,t)和f2(x,t)只是时空坐标的函数,而与具体粒子的运动速度无关,因此可推知上述关系式对粒子任意运动速度都普遍成立。代入式(5),则有
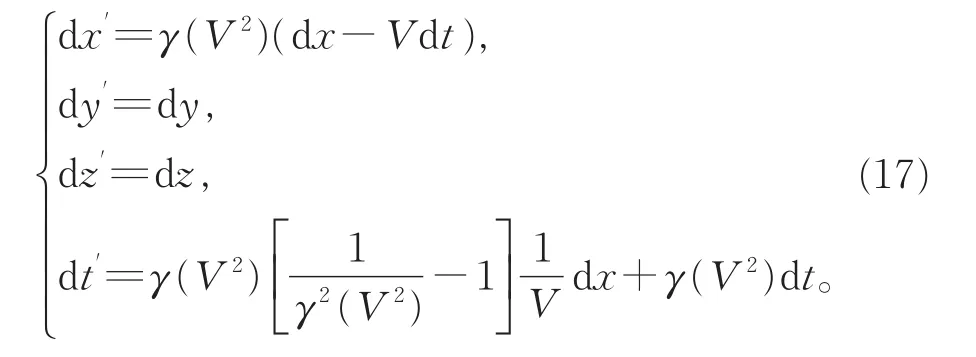
对于惯性系之间的相对运动,由于V为常量,因此γ(V2)也与时空坐标无关,对式(17)积分可得(取齐次时空变换,即令积分常数为0):
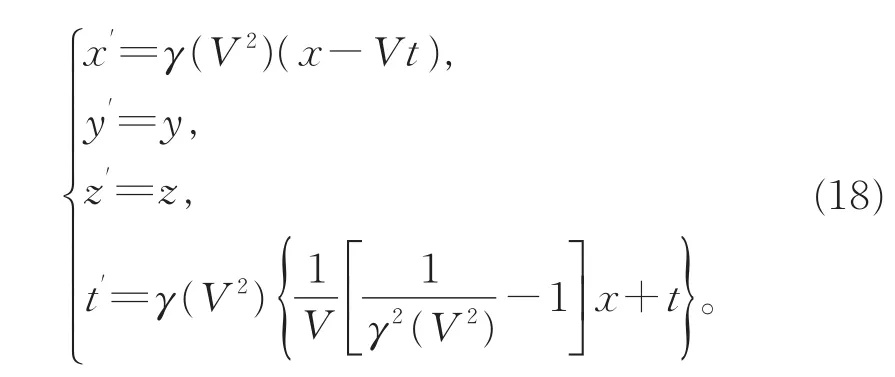
由此无须引入额外的假设,仅依据相对性原理证明了不同惯性系之间的时空变换为线性变换。而惯性系的速度变换关系则为
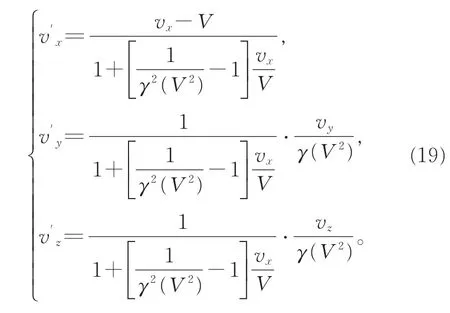
以上推导说明不同惯性系之间的时空线性变换系数与无量纲质速关系γ(V2)=m(V2)/m0的具体函数形式有关。通常在传统相对论中,利用光速不变假设建立的洛伦兹变换公式为
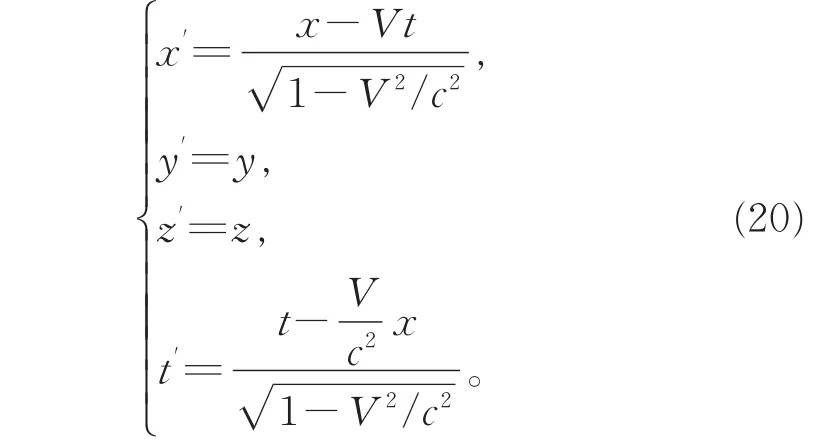
则可确定相对应的无量纲质速关系为
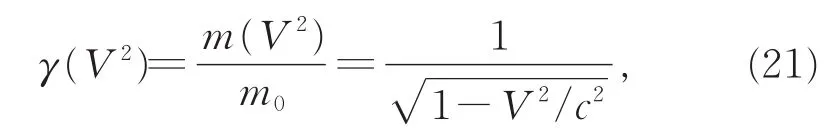
其中V为惯性系之间的相对运动速度。当粒子的运动速度为v=|v|时,粒子的质速关系则为
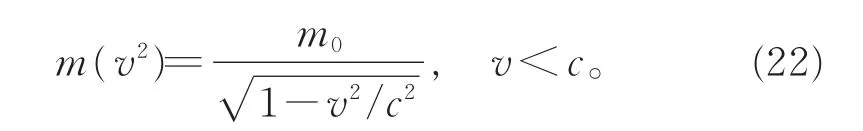
另一方面,若依据相对性原理能够求得粒子质速关系,即使不引进光速不变假设也可确定惯性系之间的时空变换公式。
2 相对论质能关系和质速关系
由于S′系和S系均为沿X方向的相对运动,因此,粒子动量在X方向分量的变换关系为(严格证明见附录 A)[15]:
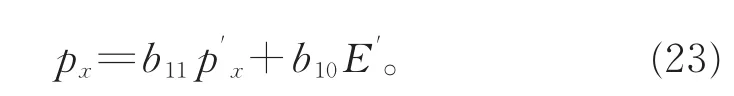
需要指出的是,动量和能量在不同参考系的线性变换特性是由广延量的物质相加性决定的,与时空是否具有平移不变性无关,即与动量和能量是否守恒无关。事实上,动量和能量的线性变换特性在非惯性系中同样成立,只是其相应的线性变换系数不再是常量,而是时空坐标的函数b=b(x,t)。
对静止在S系中即v=[0,0,0]的粒子,由式(19)可知,该粒子相对于S′系的运动速度为v'=[-V,0,0],代 入 式 (23)可 得 0=b11m(V2)(-V)+b10E(V2),即

由此可得

若一粒子在S系中垂直于X方向做相对运动,即其运动速度为v=[0,vy,vz],由式(19)可知,该粒子在S′系中的运动速度为 v'=[-V,vy/γ(V2),vz/γ(V2)],则有

即有
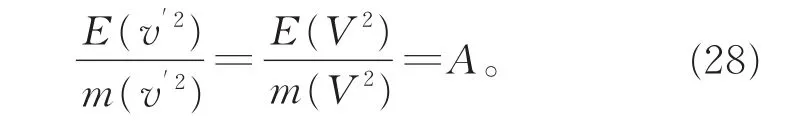
由于v′2和V2的取值互相独立,因此A必须为与粒子运动速度无关的待定常量。则无须引进光速不变假设,便可证明粒子能量正比于动质量,而与时空变换的具体形式无关。由于上述证明中不涉及相互作用过程,因此并不依赖于动量守恒和能量守恒定律,对自由粒子同样成立[15]。于是粒子能量为
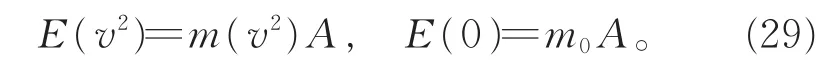
需要说明的是,上述质能关系虽然是在某种粒子运动速度的特例情况下推得,但由于粒子动量-能量在不同惯性系的线性变换系数与粒子的运动速度无关,因此,质能关系式在粒子任意运动速度下均成立。
依据粒子能量变化与动量变化的基本关系式:
可以建立有关粒子质速关系的微分方程:

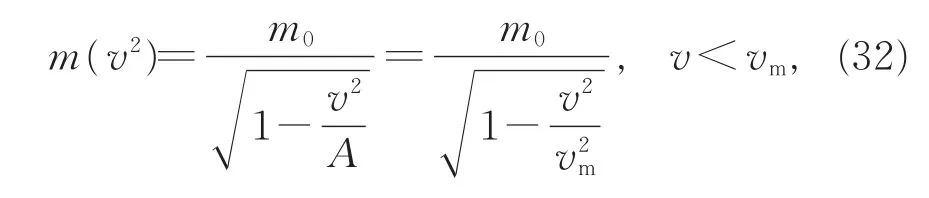
其中A=v2m,vm为普适的粒子运动速度上限[12-14]。这就意味着无须引进光速不变假设,以及不依赖动量和能量守恒定律,仅依据相对性原理即可求得不同惯性系之间时空变换的广义洛伦兹变换公式:

由式(34)不难证明极限速度vm为广义洛伦兹变换下的不变量[11],因此,若取vm=c,广义洛伦兹变换就回到了传统洛伦兹变换,而光速不变则成为了相对论的一个推论。
3 结论与讨论
3.1 证明了时空线性变换是相对性原理对于惯性系的一个推论。依据相对性原理关于惯性系的等价性,要求粒子动量、能量在不同惯性系中对于粒子速度的函数关系形式相同,则无须引进光速不变和其他额外假设,证明了惯性系之间的时空变换为线性变换。
3.2 建立起惯性系时空线性变换系数与粒子无量纲质速关系(V2)=m(V2)/m0之间的普遍联系式(16)。依据动量和能量的广延量特性,粒子动量-能量在不同参考系的变换是线性变换,其既适用于惯性系(线性变换系数为常量),亦适用于非惯性系(线性变换系数为时空坐标的函数)。在质速关系中,速度是与时间和空间相关的量,而粒子的动量和能量则依赖于动质量(即质速关系),这就在参考系的粒子动量-能量变换与时空坐标变换之间通过无量纲质速关系γ()=m)/m0建立起了关键联系,从而可用于确定参考系之间的具体变换关系式。只要依据相对性原理求得粒子无量纲质速关系γ(V2),就无须引进光速不变假设来确定时空变换关系。
3.3 完全由相对性原理证明了粒子能量正比于动质量:Ε()=m()A。该普遍的质能关系不依赖具体的参考系变换,因此A是相对论的一个基本普适常量。在质能关系基础上,通过建立和求解粒子质速关系的微分方程,求得了粒子无量纲质速关系()=进而可以最终确定惯性系时空变换的广义洛伦兹变换公式。在广义洛伦兹变换中,由更具普遍性的极限速度替代了光速c,极限速度vm的引进是满足相对性原理要求的,并不依赖于零静质量粒子的存在。的取值可由实验测量确定,无须通过引进光速不变假设事先予以限定。普适常量A=v2m是完全独立于光速而存在的,即相对论理论的建立并不依赖于光速,因此任何对光速不变假设的质疑本质上与相对论无关,其实质仅仅是质疑vm=c是否成立或是否严格成立。
3.4 证明了光速不变假设以及动量守恒和能量守恒定律都不是建立相对论的必要条件。文献[11-14]无须引进光速不变假设,通过各种相互作用过程的讨论,依据相对性原理以及动量守恒和能量守恒定律推导了广义洛伦兹变换公式。而在本文更具普遍性的推导证明中,既不需要事先假设惯性系的时空变换为线性变换,也无须讨论具体的相互作用过程,因而也不再涉及动量守恒和能量守恒定律。
3.5 建立相对论的基本理论假设只需要一个相对性原理,由此可以自动引进极限速度vm,推导出粒子的质能关系和质速关系,进而确定惯性系之间时空线性变换的广义洛伦兹变换公式,从而建立起不依赖具体相互作用和具体物质特性的更为普遍的相对论理论。它既与vm=c光速不变的传统相对论相容,又适用于可能的vm≠c的变光速或超光速现象,从而使得相对论的理论基础更加稳固,应用范围更为广泛。
感谢浙江省自然科学基金(“相对论理论的研究与改进”,编号:LY17A050001)对本研究课题的鼓励和资助!感谢美国普林斯顿高等研究院Einstein Postdoctoral Fellow戴亮对本文的有益建议。
4 附录A:粒子动量-能量变换的一般形式
由于动量和能量都是广延量,为了保证动量和能量具有广延量的物质相加性,其在不同参考系中的变换关系必须为线性变换,则粒子动量-能量在不同惯性系的变换可一般性写为(其线性变换系数事先并不假定为常量,一般允许为时空坐标的函数)
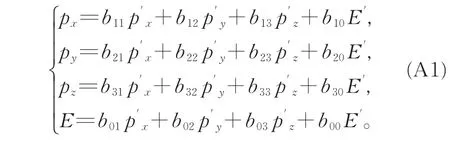
依据平动速度变换公式(6),则可证明

即有一般表达式
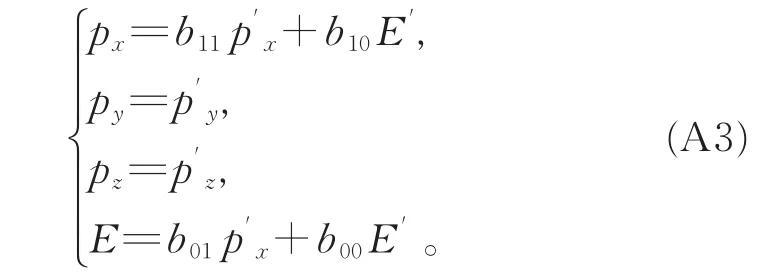
(i)证明 b12=b13=b02=b03=0。
若一粒子在S系中的运动速度为v=[vx,vy,0],则该粒子相对于S′系的运动速度为v'=[v′x,v′y,0];而若 v=[vx,-vy,0],则有 v'=[v′x,-v′y,0];因而均有 v2=v2x+v2y,v′2=v′2x+v′2y,pz=p′z=0。 由(A1)第1式得
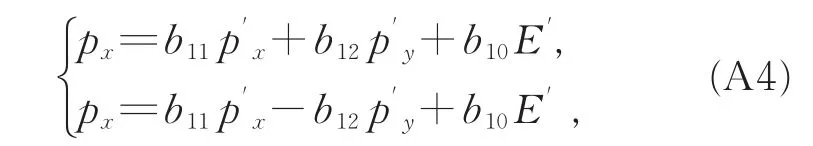
由此可得b12p′y=-b12p′
y,即有 b12=0。 由(A1)第 4式得

由此可得b02p′y=-b02p′
y,即有 b02=0。
若一粒子在S系中的运动速度为v=[vx,0,vz],则该粒子相对于S′系的运动速度为v'=[v′x,0,v′
z];而若 v=[vx,0,-vz],则有 v'=[v′x,0,-v′
z];因而均有 v2=v2x+v2z,v′2=v′2x+v′2z,py=p′y=0。由(A1)第1式得
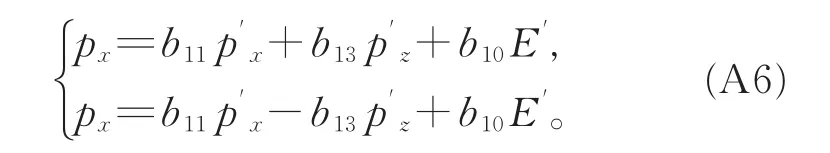
由此可得b13p′z=-b13p′
z,即有b13=0。由(A1)第4式得
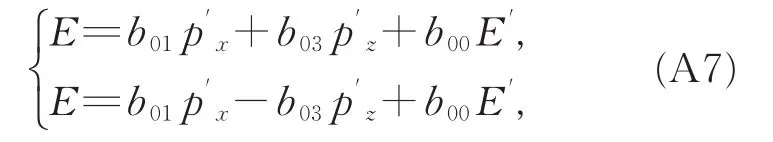
由此可得b03p′z=-b03p′
z,即有 b03=0。
(ii)证明b20=b30=b21=b31=b23=b32=0。
若一粒子在S系中的运动速度为v=[V,0,0],则该粒子将静止在 S′系中 v'=[0,0,0],即有 v′2=0。由(A1)第 2式得 0=b20E′,则有 b20=0;由(A1)第3式得0=b30E′,则有 b30=0。
若一粒子在S系中的运动速度为v=[vx,0,0],则该粒子相对于S′系的运动速度为v'=[v′x,0,0];由(A1)第 2 式得 0=b21p′x,即有 b21=0;由(A1)第 3式得0=b31p′x,则有 b31=0。
若一粒子在S系中的运动速度为v=[V,0,vz],则该粒子相对于S′系的运动速度为v'=[0,0,v′z];由(A1)第2式得 0=b23p′z,即有 b23=0。
若一粒子在S系中的运动速度为v=[V,vy,0],则该粒子相对于S′系的运动速度为v'=[0,v′y,0];由(A1)第 3式得 0=b32p′y,即有 b32=0。由此(A1)可化为

由(A8)的 py=b22(V)p′y,依据相对性原理,S′系和S系是等价对称的,其逆变换为p′y=b22(-V)py。另在空间反演下动量和速度均要反号(-py)=b22(-V)(-p′y),即 有 py=b22(-V)p′y,由 此 可 得b22(-V)=b22(V)。则有
(iii)证明b22=b33=1。

即有[b22(V)]2=1,要求满足条件b22(0)=1,则得b22=1。用类似方法可证明b33=1。
