数形结合思想在高中数学解题中的有效应用

魏金凤

摘 要：数形结合思想是高中数学解题中实用性较强的一种方法，在平常的学习和研究中注重对这种思想的灵活运用，根据题目条件合理运用图形，根据图形拓展思维，真正做到“数”和“形”的结合，从而提高学生的解题能力。以高中数学为对象，探析数形结合思想在高中数学解题中的有效应用。

关键词：数形结合思想;高中数学;解题

如今，高中数学学习中，多数同学发现问题、提出问题、勇于创新和挑战的意识还未养成，机械模仿教师方案、简单套用教学内容的现象十分普遍。学生只是知识的搬运工，无法通过掌握知识的熟练应用，透过数学概念、原理、模型等进行数学学习的深层次延伸。此外，学生对数学中的概念理解不到位，只能做到词句之间的表征结构对比，无法从内容本质上进行数形结合解题，对提高高中数学解题能力不利。在高中数学解题中使用数形结合思想，能将代数和几何问题进行灵活转化，促使复杂的问题简单化，帮助学生通过图形直接看出题目的本质，将抽象问题转化为具体图形，这也说明数形结合思想能更便捷地帮助学生理解知识，掌握知识，消化知识。

一、数学结合思想的应用价值

数形结合能让某些抽象的数学知识变得形象化和生动化，从而将抽象思维转化为具象思维，帮助学生分析和理解，在高中数学解题中有着较为广泛的应用。数形结合思想作为重要的数学思想之一，从本质上来看是将抽象的数字语言同直观的图形语言有机地结合起来，对该思想的应用，关键在于促进数字与图形彼此间的有效转化，促使数字问题实现图形化，图形问题能够实现数字化，借助这种转化，让数学问题从复杂向简单转化，使解题过程事半功倍。对于数形结合思想来说，其主要分为两种：一为以图形性质为条件，对数值进行求解，即借助图形的直观性对数字间关系加以解决;二为以数字为条件，对图形性质进行分析，即借助数字的严谨及精确性，对图形性质进行分析[1]。随着高中数学问题抽象化加深，数学学习中知识点理解困难形成学习阻碍，学习压力提升。而数形结合不仅是一种教学方法，更是一种思维方式和解题策略。在抽象知识的学习中高效应用数形结合思想可以对一些问题采用图形表示，利用图形对数学语言进行解释更为直观，从而解决抽象的、较难理解的数学问题，帮助学生降低高中数学解题难点[2]。在实际解题过程中，学生可通过题目已知条件，利用图形获取答案，找出其中的数量关系。

二、数形结合思想的应用

（一）在集合问题解题中的应用

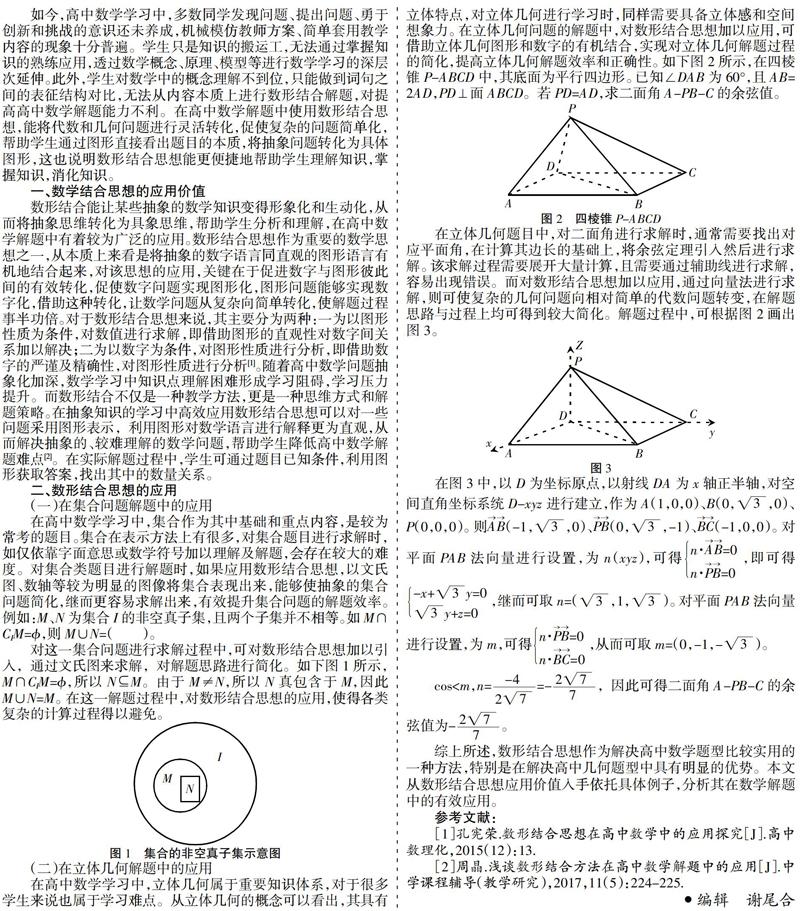
在高中数学学习中，集合作为其中基础和重点内容，是较为常考的题目。集合在表示方法上有很多，对集合题目进行求解时，如仅依靠字面意思或数学符号加以理解及解题，会存在较大的难度。对集合类题目进行解题时，如果应用数形结合思想，以文氏图、数轴等较为明显的图像将集合表现出来，能够使抽象的集合问题简化，继而更容易求解出来，有效提升集合问题的解题效率。例如：M、N为集合I的非空真子集，且两个子集并不相等。如M∩CIM=？准，则M∪N=（  ）。

对这一集合问题进行求解过程中，可对数形结合思想加以引入，通过文氏图来求解，对解题思路进行简化。如下图1所示，M∩CIM=？准，所以N？哿M。由于M≠N，所以N真包含于M，因此M∪N=M。在这一解题过程中，对数形结合思想的应用，使得各类复杂的计算过程得以避免。

（二）在立体几何解题中的应用

在高中数学学习中，立体几何属于重要知识体系，对于很多学生来说也属于学习难点。从立体几何的概念可以看出，其具有立体特点，对立体几何进行学习时，同样需要具备立体感和空间想象力。在立体几何问题的解题中，对数形结合思想加以应用，可借助立体几何图形和数字的有机结合，实现对立体几何解题过程的简化，提高立体几何解题效率和正确性。如下图2所示，在四棱锥P-ABCD中，其底面为平行四边形。已知∠DAB为60°，且AB=2AD，PD⊥面ABCD。若PD=AD，求二面角A-PB-C的余弦值。

在立体几何题目中，对二面角进行求解时，通常需要找出对应平面角，在计算其边长的基础上，将余弦定理引入然后进行求解。该求解过程需要展开大量计算，且需要通过辅助线进行求解，容易出现错误。而对数形结合思想加以应用，通过向量法进行求解，则可使复杂的几何问题向相对简单的代数问题转变，在解题思路与过程上均可得到较大简化。解题过程中，可根据图2画出图3。

综上所述，数形结合思想作为解决高中数学题型比较实用的一种方法，特别是在解决高中几何题型中具有明显的优势。本文从数形结合思想应用价值入手依托具体例子，分析其在数学解题中的有效应用。

参考文献：

[1]孔宪荣.数形结合思想在高中数学中的应用探究[J].高中數理化，2015（12）：13.

[2]周晶.浅谈数形结合方法在高中数学解题中的应用[J].中学课程辅导（教学研究），2017，11（5）：224-225.

编辑 谢尾合