可以解释的缘分
2019-08-13竹林风
竹林风
平平淡淡的生活中,我们总会遇到一些让人觉得特别意外的事情,比如突然中了彩票,跟同桌是同一天生日,在马路上碰到了很久很久没联系的同学……有不少人会认为这些意外是缘分或者天意。但其实,我们所谓的缘分有时并不是突然冒出来的,是可以解释的。
飞机上的“朋友”
在飞往某地的飞机上,无聊的杰克和身边素不相识的汤姆聊了起来。
杰克:“这么说,你是从波士顿来的了。我的老朋友露茜是那儿的律师。”
汤姆:“这个世界是多么小啊!她是我妻子最好的朋友,在家时常听我妻子说到她。”
杰克:“天哪,真是太巧了!对了,你的妻子是不是叫玛丽?”
汤姆:“对啊!你认识她吗?
杰克:“当然,我们去年见过。有一次露茜带她出来,我们一起吃过饭。”
…………
碰到陌生人,尤其是在远离家乡的地方碰到一个陌生人,发现对方与自己有共同朋友时,相信谁都会感到非常惊讶,因为一般人会认为这种巧合很不容易碰到。
你是不是也想惊呼杰克和汤姆的缘分?那我告诉你大可不必,因为统计学家说这种缘分很容易发生。
统计学家研究发现,如果在美国任选两个人,平均每个人认识大约1000个人。这时,这两个人彼此认识的概率大约是1 1000000。而他们有一个共同的朋友的概率却急剧升高到1 100。至于他们可由一连串熟人间接联系上的概率,实际上高于99%。换言之,如果布朗和史密斯是在美国任意选出的两个人,上面的结论就是:一个认识布朗的人,有很大的可能性认识一个史密斯熟识的人。这就是“小世界理论”。
真是太不可思议了!统计学家说很容易发生,但我怎么没遇到过。
噜噜啊,那是统计得出来的结论,容易发生并不代表一定发生。
真相大白
小世界理论,即世界上的任意两个人之间都可以通过六层以内的朋友链而联系起来。也就是说,最多通过5个人,你便能够认识英国女王、甚至任何国家的领导人。
假如我们每个人都至少认识25个人,而这25个人又分别各认识另外的25个人……以此类推,计算结果告诉我们,经过7次介绍之后(间隔6个人),我们便能和257(7个25相乘),即60多亿人联系在一起。
起初,这个理论难以得到普通人的认可,这和我们的实际经验不相符。因为如果不借助网络,仅通过人脉关系,我们想认识某个名人还是有一定难度的,需要的中间介绍人很可能不止6个人。不过身处互联网时代,大家开始慢慢相信这个理论了。事实上,很多社交网络就是基于这个理论构建的。如Facebook、QQ、微博、微信等都会显示你有多少好友,你的好友又关注了哪些好友,甚至它们会告诉你,你是通过谁认识了这些好友,还会根据你的“特点”给你进行好友推荐。如此一来,我们的朋友圈便一步步被扩大,我们得以认识了一些在生活中完全接触不到的人,包括一些名人。
六个人的聚会
那次不经意的闲聊,让杰克和汤姆成了好朋友。这不,杰克去波士顿出差,刚好赶上了汤姆在家组织聚会。特别的是,这是一个六人聚会,也就是除了汤姆,还有5个人。
“你好!”
“你好!很高兴认识你!”
人到齐了,大家都很热情,相互握手打招呼。
“杰克,过来!我给你介绍一位朋友。”汤姆朝杰克挥手喊道。
听到汤姆的呼唤,杰克快步走过去。这时,让人意想不到的事情发生了。
“天哪,太巧了吧!艾伦,你什么时候来波士顿的?”杰克惊讶地说道。
汤姆看了一眼对面的艾伦,又看了一眼杰克,问:“你们认识?”
“是啊,汤姆!原来你要给我介绍的人是艾伦啊!”杰克笑着说道。
“我们认识好多年了,上个月才刚见过面呢。”艾伦把手搭在杰克肩上。
…………
其实,在任意6个人的聚会上,有3个人彼此认识,或者有3个人彼此不认识,这是很正常的,而且这两种情况必有其一会发生。瞧你,又惊讶得合不拢嘴了。不相信?等着,我这就给你证明。
真相大白
在6个人中任选一人作为主人,而他与其他5个人的关系可以分成两类:认识的和不认识的。由抽屉原理可知,将5个人分为两类,则有一类至少有3个人。因为把m个东西任意分放进n个空抽屉里(m>n),那么一定有一个抽屉被放进了至少2个东西。
假设主人认识的有3个人,而如果这3个人互相不认识,则刚好满足“3个人彼此不认识”。否则,至少有2个人彼此认识,再加上主人,就有了彼此认识的3个人,满足“3个人彼此认识”。也就是说,不管怎样,两种情况必有其一发生。
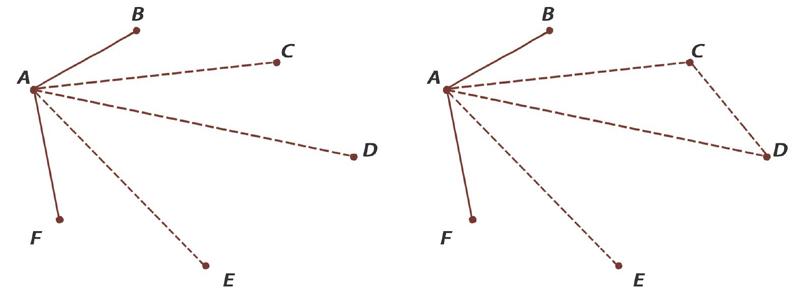
我们也可以尝试用画图的方法来说明。把“人”用“点”表示,人与人的“关系”用实线和虚线表示:2个人相互认识用实线相连,2个人相互不认识则用虚线相连。
从主人A连出的线,不是虚线就是实线,因此一定有一种线的数目大于等于3。
不妨设AC、AD、AE是虚线,这时CD若是虚线,则A、C、D就是相互不认识的3人,同理,CE或DE是虚线时,我们也可以找到3个相互不认识的人。也就是说,当CD、CE或DE任一条为虚线时,我们总会得到一个由3条虚线组成的三角形,即存在相互不认识的3人。而如果CD、CE和DE都是实线,那么△CDE成为由3条实线组成的三角形,则C、D、E就是相互认识的3人。
不管怎么说,最后总会出现一个由同种线构成的三角形,所以6个人聚会,会有3个人相互认识或者相互不认识。
万万沒想到,缘分原来是可以解释的。
很多时候,缘分并没有我们所认为的那么神奇。
