卷烟滤棒成型送丝喷嘴内气流场的数值模拟
2019-08-13杨占平郝习波曾泳春
杨占平,郝习波,窦 峰,曾泳春*
1. 南通醋酸纤维有限公司,江苏省南通市崇川区钟秀中路109 号 226008
2. 东华大学纺织学院,上海市松江区人民北路2999 号 201620
滤棒是卷烟的主要组成部分,其作用是过滤烟气并减少烟气中的有害成分,因此对卷烟品质具有重要影响。卷烟滤嘴棒主要由成型纸、丝束、搭口胶组成[1-3]。送丝喷嘴是将开松后丝束填充入成型机烟腔,并与成型纸同步包裹后形成滤棒的关键生产设备。送丝喷嘴利用文丘里效应,在喷嘴内形成气流场并通过该流场完成丝束牵引[4],气流场的分布直接决定了丝束牵引质量,因此对送丝喷嘴内气流场进行研究具有重要意义。目前使用CFD(Computer Fluid Dynamics)技术对喷嘴内气流场以及纤维运动进行数值模拟研究已有较多报道。林惠婷[5]利用CFD 技术研究了转杯纺纱器和梳棉通道中的气流场分布与纤维运动;裴泽光[6]、李美玲[7]使用CFD 技术先后研究了涡流纺喷嘴腔体内的气流场分布与纤维运动情况。CFD 克服了理论分析方法求解非线性问题困难、实验测试受限制且经费、人力和物力消耗大等缺点[4],在汽车内燃机[8]、飞行器[9]、船舶[10]、暖通系统[11]等工业领域被广泛应用于解决与流体相关的问题。为此,应用多物理场数值模拟软件Comsol Multiphysics 对卷烟滤棒成型送丝喷嘴内气流场进行模拟,通过研究气流场对纤维运动的影响,建立纤维运动模型并利用Matlab 软件进行编程求解,以期解决因喷嘴内气流场分布不稳定导致滤棒吸阻波动等问题。
1 送丝喷嘴气流场建模
图1 为送丝喷嘴的剖面图。高速气流和丝束分别从入口进入喷嘴腔体内,气流经过多通道分布器后,从内外套之间间隙进入纤维牵伸区域对纤维施加牵引力。
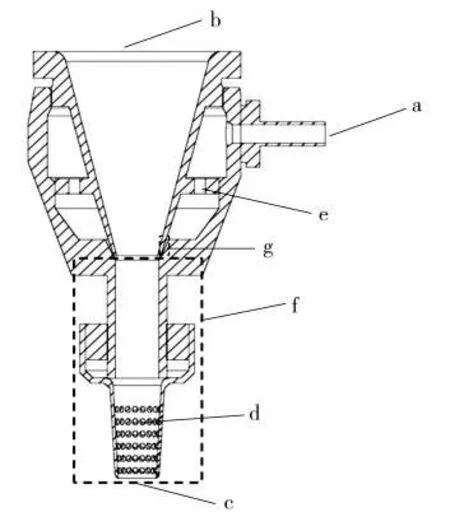
图1 送丝喷嘴剖面图Fig.1 Cross section profile of tow transport jet
由于送丝喷嘴结构复杂,无法将其流体域简化为二维,因此对其气流场进行三维模拟。利用三维CAD 设计软件Solidworks 完成流体域几何模型的构建,见图2。原点位于底部出口的中心。
1.1 控制方程
送丝喷嘴内流体的流动主要遵守物理守恒定律,包括质量守恒定律、动量守恒定律和能量守恒定律。
1.1.1 质量守恒方程
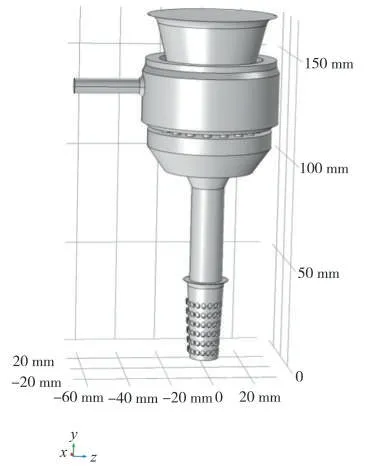
图2 喷嘴流体域几何模型Fig.2 Geometry model of fluid domain of tow transport jet
质量守恒方程又称为连续性方程,该方程描述了流体微元体在一定时间内,其增加的质量等于响应时间内流入与流出该微元体的质量之差。在笛卡尔直角坐标系下,质量守恒方程的微分形式可表述为:

1.1.2 动量守恒方程
动量守恒方程又称为Navier-Stokes 方程,其表达式为:
婴幼儿的蛋白质需求量并没有家长们想象得那么高,例如,每100毫升母乳中含有蛋白质1克左右(这需要根据母亲的饮食结构而定),配方奶中所含有的蛋白质含量是母乳的2倍,1~6个月的宝宝每天喝700~800毫升的奶即可满足日常生长发育的需求。

式中:ρ为气体密度;t 为时间;u 为速度矢量;ui(i=1,2,3)为u 在坐标分量方向上的分量;μ为动力黏度;p 为压力;Si为xi方向上的广义源项。
1.1.3 能量守恒方程
流动系统如果包含热交换,则必须满足能量守恒定律,即热力学第一定律,其能量方程可表述为:

式中:T 为温度;kt为流体传热系数;cp为比热容;ST为黏性耗散项。
由于不存在传热过程,所以本文中模型不考虑能量交换。为此,采用标准的k-ε模型对湍流流动进行求解[12]。
1.2 网格划分和边界条件设定
由于模型几何结构复杂,本文中采用自由四面体进行非结构化网格划分。在模型壁面处添加边界层,以提高壁面附近气流场的解析度。因计算区域存在较多尖角,且这些尖角会增加收敛难度,因此在计算区域的弯角处进行网格细化,网格单元划分总数为190 809,划分结果见图3。

图3 喷嘴计算区域网格划分Fig.3 Meshing diagram of computational domain of jet
送丝喷嘴内气流场模拟的边界条件为:①入口边界,计算区域只包含一个气流入口,入口条件设为压力入口,标准大气压为参考值,入口压力值设为20 000 Pa;②出口边界,气流出口位于图1 中的c 和d,出口处气压等于外界大气压,因此出口压力设为0;③开放边界,图1 中纤维入口b 存在气流进出,因此将其设为开放边界;④壁面边界,将空气视为黏性流体,因此送丝喷嘴所有固体壁面设为无滑移壁面边界。
2 纤维在气流场中的运动模拟
2.1 纤维运动模型的建立
本文中建立纤维模型的目的在于考察送丝喷嘴内气流场对纤维运动的影响。为简化计算,假设纤维由一系列球体构成,见图4。

图4 纤维球链模型示意图Fig.4 Schematic diagram of fiber model
图4 中,每个球体的直径等于纤维直径,密度等于纤维密度,则纤维质量mf为:

本模型中只考虑空气阻力对纤维的作用。在笛卡尔坐标系下,将空气阻力分解为x,y,z 三个方向的分力,分别为:

式中:CD为空气阻力系数;ρa为空气密度;va为空气速度;vf为纤维速度。
空气阻力系数CD是与雷诺数相关的常数,计算公式为:
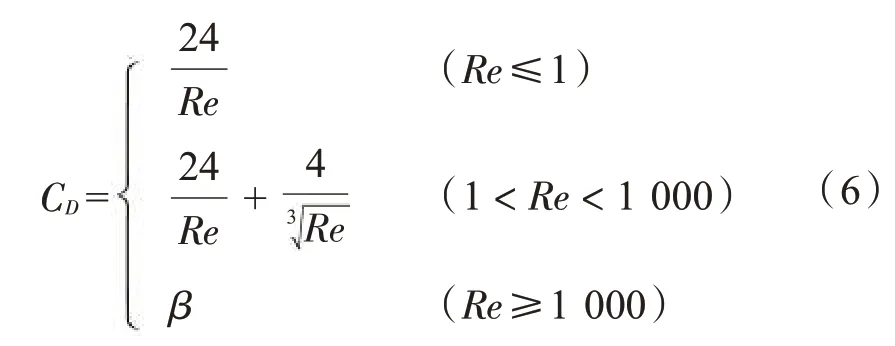
雷诺数Re 定义为:

式中:μ为空气运动黏度。
根据牛顿第二定律,可得纤维在空气中的运动方程为:
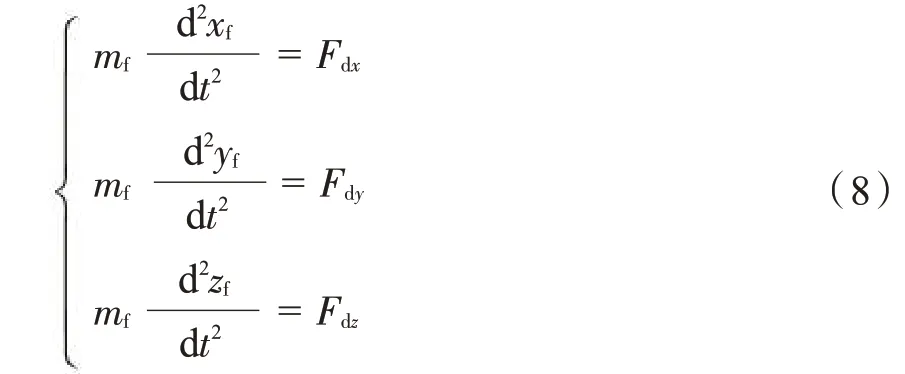
式中:xf,yf,zf分别为纤维在t 时刻的位置。
2.2 模型参数
已知参数:纤维直径df=2×10-5m,纤维密度ρf=1.54×103kg/m3,空气密度ρa=1.29 kg/m3,空气运动黏度μ=1.48×10-7m2/s。初始条件:在y=89 mm位置的x-z 平面上选择41 个点作为起始位置进行计算,起始点分布见图5。纤维运动方向与送丝喷嘴中心轴平行,从起始位置开始以5.8 m/s 速度进入计算区域。
2.3 计算方法
①给定初始时刻(t=0)时的纤维初始速度和初始位置;②根据对喷嘴内气流场的模拟,得到纤维运动区域的气流速度矢量;③根据式(4)~(7)计算得到纤维所受到的气流场阻力;④根据式(8)计算得到纤维在t+Δt 时刻的位置;⑤重复以上计算,即可得到纤维随时间变化的轨迹。
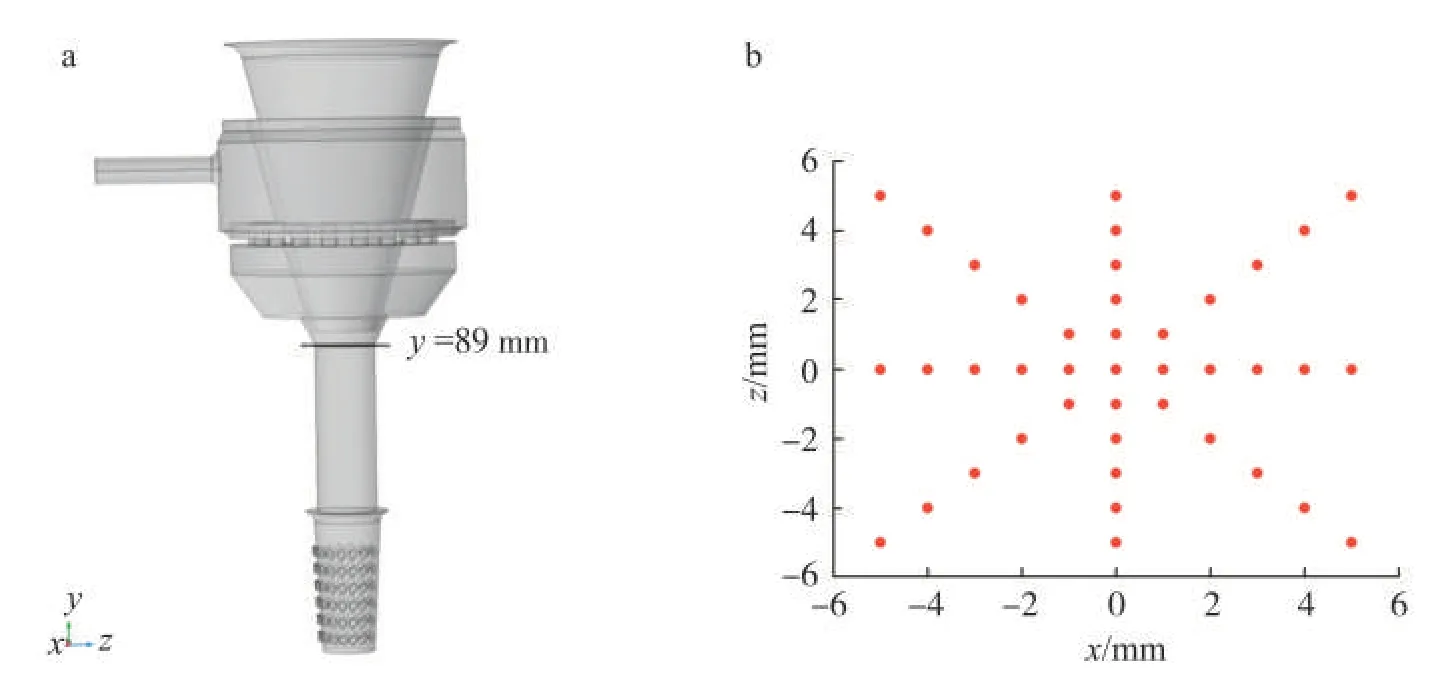
图5 纤维运动的起始位置Fig.5 Initial positions of fiber movement
3 结果与讨论
3.1 喷嘴内气流场分析
由图6 可见,气流从入口管道进入喷嘴腔体后在腔体内形成较大涡旋,经过分流器后大涡分散成小涡,气流经过内外套之间的间隙后涡旋基本消失,流线近似于直线状态,这种状态有利于纤维的伸展。由图7 可以清楚地观察到气流场内气流速度分布。由图7a 可见,入口处的气流速度最大,进入腔体后由于流域空间变大,在相同气流流量下速度降低。气流在进入下端出口管道后,由于管道收窄速度再次增高。由图7b 可见,气流从入口管道进入腔体后,在腔体内部分散不均匀,靠近入口处的气流速度较高,经过分流器分散后,内部速度分布变得较为均匀。由图7a 还可以看出,气流速度在下部出口管道中并不是呈对称分布,这可能是由于气流入口不对称分布造成的。气流从喷嘴内外套间隙中喷射进入出口管道后,靠近壁面处的气流流速较高,并且在向出口运动的过程中逐渐向管道中心位置扩散,在靠近出口处汇合。
3.2 纤维轨迹计算结果
由图8 可见,红色曲线为纤维轨迹,蓝色箭头为气流的合速度矢量。纤维与气流的速度差会产生气流对纤维的作用力,纤维在气流的作用下向出口运动,但由于气流速度在z 轴与x 轴方向上存在分速度,且气流速度在出口管道中不对称分布,会造成纤维在运动过程中发生偏移。因此,纤维在出口管道中的横向(x 轴与z 轴方向)偏移有可能导致纤维质量波动。
3.3 内外套间隙的影响

图6 喷嘴内气流场流线图Fig.6 Streamlines of air flow field inside jet

图7 不同位置的喷嘴气流场切面图Fig.7 Cross sections of air flow field inside jet

图8 纤维在气流场中的运动轨迹Fig.8 Movement trajectory of fibers in air flow field
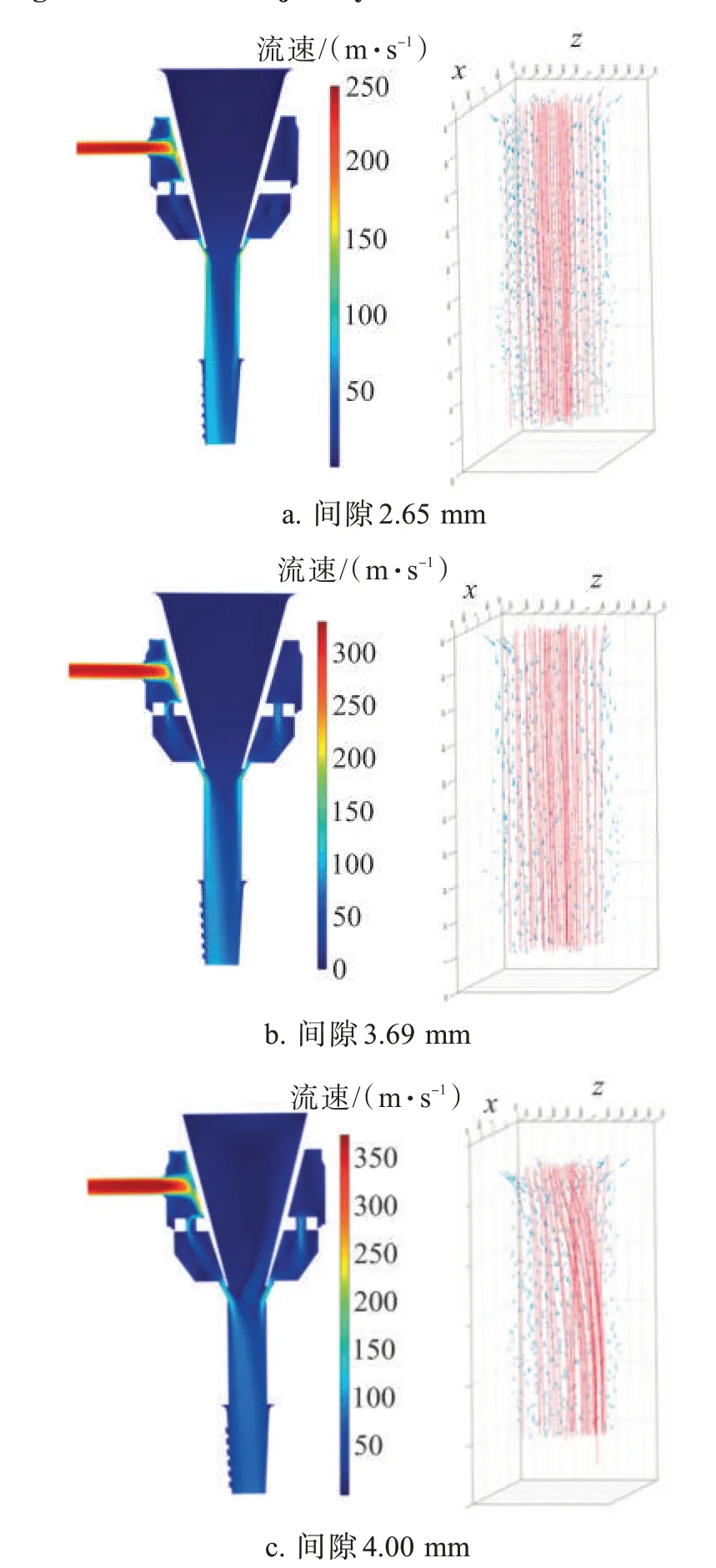
图9 不同内外套间隙下喷嘴内气流场分布与纤维运动轨迹Fig.9 Air flow field distribution and movement trajectory inside jets with different clearances between sleeves
图9 为相同入口压力(20 000 Pa)、不同内外套间隙(2.65 mm,3.69 mm,4.00 mm)下喷嘴内气流场分布与纤维运动轨迹。可见,随着间隙的增加,气流在出口管道中的不对称分布越来越明显,且整体流速也随之增加。为进一步比较,利用式(12)和(13)计算纤维在x 轴与z 轴方向的平均偏移距离。

由表1 可见,纤维向着z 轴正方向偏移,并且随着间隙增加纤维平均偏移距离增大,但在x 轴方向产生的偏移相对较小。由于纤维在运动过程中的横向偏移可能会导致滤棒质量波动,因此减小喷嘴内外套间的隔隙,理论上可以降低因滤棒质量波动而造成的吸阻波动。

表1 不同内外套间隙下纤维的平均偏移距离Tab.1 Average deviation of fiber alignment inside jets with different clearances between sleeves (mm)
4 结论
通过对卷烟滤棒送丝喷嘴内气流场进行流体动力学模拟,并结合纤维运动模型进行送丝效果分析,得到以下结论:①喷嘴内的分流器起到均匀分散气流的作用,但在喷嘴下部出口管道中,气流场会出现不对称分布,并且喷嘴内外套间隙越大其不对称性越明显;②由于气流场分布不对称,纤维在喷嘴内部运动会产生偏移,喷嘴内外套间隙越大,纤维的平均偏移距离越大,偏移可能会造成滤棒质量波动进而导致吸阻不均匀。因此,减小喷嘴内外套间隙可以降低滤棒吸阻波动。
