基于扩展卡尔曼滤波器的卫星平面轨道估计

蒋 虎，李天姣，任 波

(沈阳理工大学 装备工程学院，辽宁 沈阳110159)

卫星的平面轨道估计无论是在执行航天任务中，还是在太阳系各种小天体的发现过程中，都是不可缺少的工作.卫星轨道是由卫星的初始位置和速度、卫星所受作用力确定的[1].卫星实际的运动轨迹受多种非地球引力的影响，如地球非球形引力、日月引力等.地面观测站的雷达受天气等原因的影响而无法保证观测精度，因此在进行卫星平面轨道估计时容易产生轨道偏离[2].具体来说，因为卫星在运动中受多种摄动力的复杂作用，利用地面监控系统对卫星进行监测，难以可靠、准确地测定这些作用力，并且无法掌握它们的作用规律，所以卫星平面轨道估计时会产生较大的误差[3-4].

卫星轨道的确定应根据卫星轨道的当前观测信息，对下一时刻的轨道信息进行估计，通常使用卡尔曼滤波器，而卫星轨道运动模型是非线性的，因此应采用扩展卡尔曼滤波器(EKF)来实现对卫星平面轨道运动的估计[5].为了尽量减小卫星平面轨道估计的误差，降低各种干扰因素的影响，本文拟引入扩展卡尔曼滤波器.

1 扩展卡尔曼滤波器在卫星平面轨道估计中的应用

扩展卡尔曼滤波器采用将非线性系统线性化之后再滤波的算法.与线性化滤波相比，其优势在于能够保证滤波偏差足够小.不同于卡尔曼滤波器的是，扩展卡尔曼滤波器要对状态方程和观测方程中非线性部分进行泰勒展开，求得近似的线性化方程，即求出雅可比矩阵后进行卡尔曼滤波算法递推估计，从而实现对复杂的卫星轨道运动的估计[6-7].

设随机非线性离散系统方程为：

(1)

式中：Xk为状态向量；Zk为观测向量；f[·]为状态非线性函数；h[·]为观测非线性函数；Γk-1为噪声输入矩阵；Wk-1、Vk分别为系统离散状态噪声和观测噪声，均为零均值白噪声序列，即

(2)

式中，Qk-1、Rk分别为非负定系统过程噪声方差阵和正定观测噪声方差阵.

式(1)对应的线性状态空间模型为：

(3)

式中：Φk,k-1是函数f[·]的雅可比矩阵；Hk是函数h[·]的雅可比矩阵.

与卡尔曼滤波算法不同的是，扩展卡尔曼滤波算法需要将式(1)中非线性部分线性化，并通过下列方法计算出Φk,k-1和Hk.

(4)

式中：n为状态向量的维数；Φk,k-1为n×n维矩阵.

(5)

式中：m为观测向量的维数；Hk为m×n维矩阵.

扩展卡尔曼滤波器为：

(6)

通过式(6)，可估计卫星平面轨道.卫星平面轨道扩展卡尔曼估计的原理(图1)，在于利用卫星轨道运动上一时刻的状态值和当前时刻的雷达观测值加权再求和，来估计卫星平面轨道.

图1 卫星平面轨道扩展卡尔曼估计原理图

对图1分析可知，扩展卡尔曼滤波处理既能保持卫星的正常运动状态，又能保证估计的精度.

2 卫星平面轨道运动模型

在地球万有引力的作用下，卫星的运动轨迹是一个椭圆，这个椭圆所在的平面被称为轨道平面.在只考虑地心引力而不考虑多种摄动力影响的理想状态下，卫星平面轨道运动模型如图2所示.建立该模型后，可将地心设置为坐标原点O，地心正上方p点设为卫星运动起始点，而且，以卫星到地心的距离和卫星偏转角度来观测卫星的运动.

图2 卫星平面轨道运动模型

卫星在规定轨道中运动时受到地心引力、日月引力、太阳辐射压力、地球非球形引力、大气阻力及潮汐力等的作用.除地心引力外，其他摄动力的合力对卫星运动的影响很小.卫星运动的作用力和相应加速度如表1所示[10].

根据卫星到地心的距离和卫星偏转角度建立的卫星平面轨道运动控制方程[11]为：

(7)

式中：r为卫星到地心(又称吸引点)的距离；θ为以Y轴方向为参考偏转的角度(又称角位移)；m、g分别为地球质量和万有引力常数；ξr和ξθ均为连续时间不相关的零均值高斯白噪声.

2.1 卫星平面轨道运动状态方程

设卫星运动状态向量为：

(8)

则结合式(7)可得如下卫星运动状态方程：

(9)

(10)

(11)

(12)

(13)

式中，ξr(k)和ξθ(k)均为离散不相关的零均值高斯白噪声.

2.2 卫星平面轨道运动离散观测方程

卫星平面轨道运动的离散观测方程为：

(14)

(15)

观测矩阵可表示为：

(16)

2.3 卫星平面轨道运动离散线性化模型

与式(10)对应的离散线性化模型为:

(17)

对式(10)进行泰勒展开可求出函数fS[·]的雅可比矩阵，即

(18)

综上，利用扩展卡尔曼滤波器可以估计卫星平面轨道(r(k),θ(k)).

3 仿真与结果分析

3.1 卫星平面轨道运动轨迹

在不加入过程噪声的情况下，卫星的真实轨迹是一个椭圆.根据卫星偏转角度，将状态量中卫星到地心距离分解为X轴和Y轴方向两个分量，并将卫星在轨道中具体位置用其坐标(X，Y)来表示.根据卫星平面轨道运动模型得到的仿真结果如图3所示.

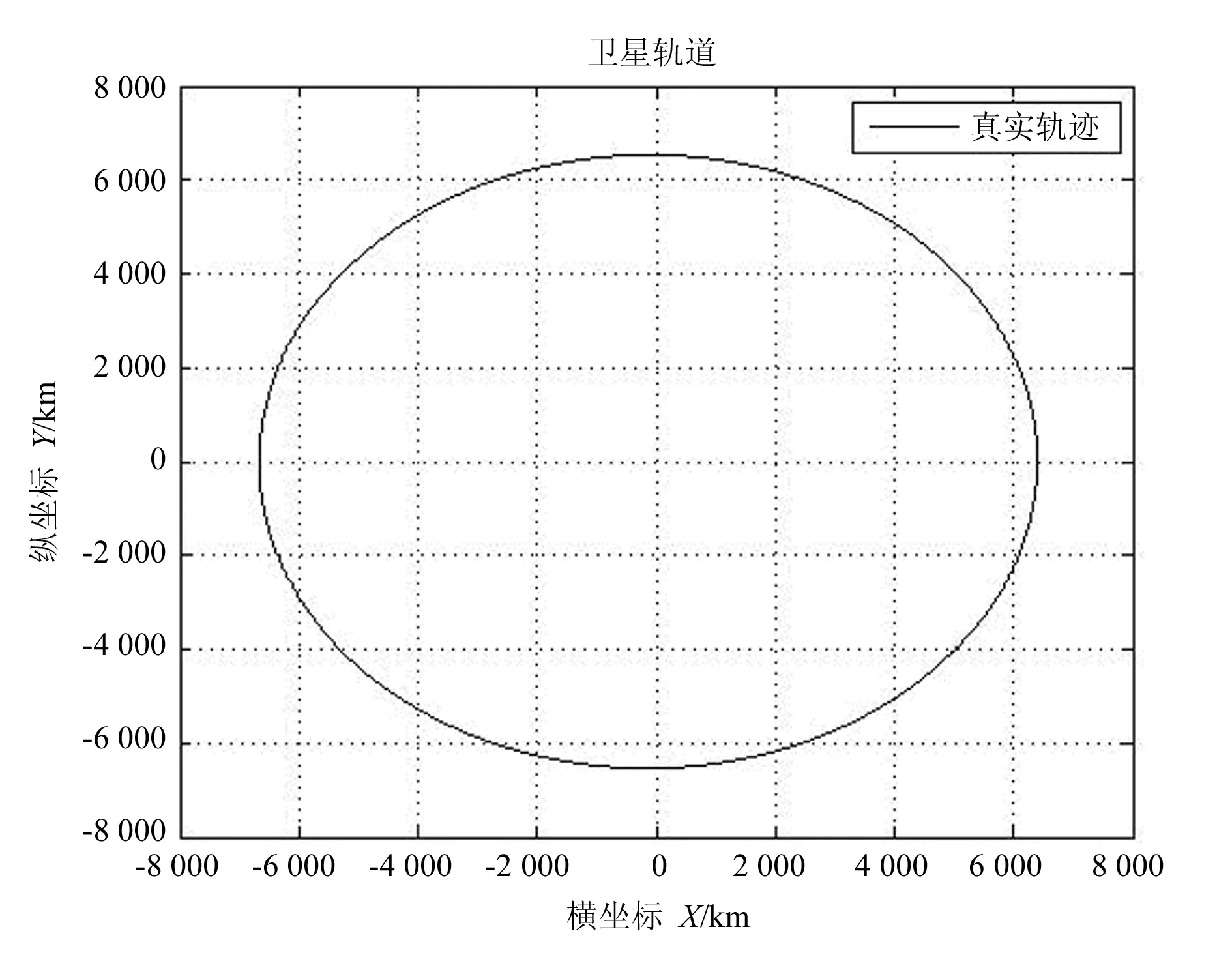
图3 卫星平面轨道运动仿真结果

对比图2和图3可知，卫星平面轨道运动仿真结果与理论的卫星平面轨道一致.

3.2 卫星到地心距离与卫星偏转角度的变化

3.2.1 卫星到地心距离的变化

在卫星平面轨道估计中，卫星到地心的距离和卫星偏转角度是重点.

通过仿真，卫星到地心距离随采样时间的变化情况如图4所示.

图4 卫星到地心距离随采样时间的变化情况

从图4(a)可以看出，随着采样时间的增加，卫星到地心距离的变化是一个先增后减的过程，因此卫星的平面运动轨迹是椭圆形且是偏心的.从图4(b)可以看出，扩展卡尔曼滤波器对卫星平面轨道的估计效果较好，滤波后卫星到地心的距离误差可控制在1 km以内，符合工程实际的需要.

3.2.2 卫星偏转角度的变化

通过仿真，卫星偏转角度随采样时间的变化情况如图5所示.图5中，对应于卫星偏转角度的真实值、观测值和扩展卡尔曼滤波值，分别用实线、虚线和星形线来表示.

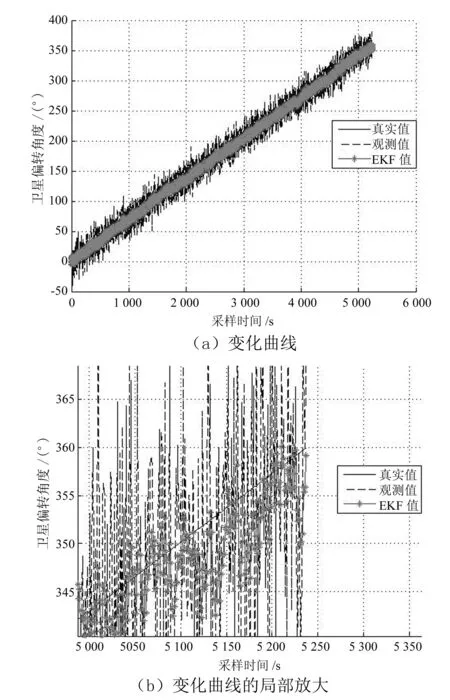
图5 卫星偏转角度随采样时间的变化情况

从图5(a)可以看出，经扩展卡尔曼滤波处理，卫星偏转角度的变化比真实值和雷达观测值的规律性更强.从图5(b)可以看出，对应于EKF值，卫星偏转的最终角度刚好达到了360°，即在这段时间内，卫星刚好转动一周.

3.3 卫星平面轨道的估计误差

针对卫星到地心的距离和卫星偏转角度，分别用雷达观测值和扩展卡尔曼滤波估计值，与真实值进行比较.雷达观测和EKF估计的误差效果如图6所示.

图6 雷达观测和EKF估计的误差效果

4 结束语

卫星在地心引力作用下的运动轨迹为椭圆形.卫星平面轨道运动的仿真结果表明，利用扩展卡尔曼滤波器对卫星轨道估计是合理的，可以显著提高卫星平面轨道的估计精度，在工程应用中具有意义.

本文建立的是二维模型，未来可通过三维模型对卫星轨道运动进行估计，并且在建模的过程中要全面考虑多种摄动力的影响.