基于螺旋理论的环形桁架式可展天线构型综合

韩 博，许允斗,2，韩媛媛，姚建涛,2，赵永生,2

(1. 燕山大学河北省并联机器人与机电系统实验室，秦皇岛 066004；2. 燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛 066004；3.衡水学院数学与计算机科学系，衡水 053000)

0 引 言

随着航天技术的不断发展，各类航天器及其功能载荷中所用的机构尺寸越来越大，空间可展开机构可以在储存和运输时处于收拢状态，在轨工作时展开，这种特点使其在各类卫星平台、航天飞行器以及空间站上得到了广泛的应用，并逐渐成为了航空航天领域的研究热点之一[1-4]。

空间可展开机构在航空航天领域的一个重要应用是作为大口径天线的展开与支撑机构，目前在轨运行的大口径星载天线主要包括四面体构架式可展开天线、环形桁架式可展开天线、径向肋式可展开天线以及环柱形可展开天线等[5-9]。环形桁架式可展开天线具有大收展比和低面密度的特点，相较于其他类型的可展开天线，随着口径的不断增大，其质量增加幅度较小，并不随口径成比例增加，是空间大口径天线较为理想的结构形式[10-12]。

美国于2000年发射了由NGST公司研发成功的AstroMesh环形桁架式展开天线[13]，这是大口径环形桁架天线一次成功的在轨应用，Escrig[14]于1985年提出了一种Pactruss双层环形桁架可展开机构，可以改善单层环形桁架机构在口径较大时刚度较低的问题，You等[15]基于剪叉机构研制了一种双层环形桁架机构样机。国内学者关于环形桁架可展开天线机构也进行了一系列研究，Guan等[16]研制了单、双层环形桁架可展开天线机构原理样机，史创等[17]基于曲柄滑块式平面可展开机构单元设计了环形桁架式可展开天线机构，并制作了原理样机。总体而言，目前在轨运行的环形桁架式可展开天线机构的类型仍然较少。

在空间可展开天线机构的构型方面，相关研究人员进行了一系列研究，取得了较为丰硕的研究成果。Lu等[18]采用Hoekens直线运动单元机构组成了一种平面式可展天线结构，Vu等[19]基于一种金字塔式的可展开机构单元组合得到了多种可展开天线机构，广晨汉等[20]由单顶点多折痕折纸形式得到启发，构造了小卫星上应用的空间折展机构，文献[21-23]基于对称型机构单元构造了多种空间伸展臂和空间可展开天线机构，文献[24]针对一列可展帆板进行了研究，文献[25-26]研究了Bennet和Bricard连杆机构在空间可展开机构中的应用，文献[27]和文献[28]分别基于Myard机构和剪叉机构构造了大型可展开天线机构。这些文献多为采用现有机构或者直接提出新型机构来构造可展开机构，并不涉及空间可展开天线机构的构型综合方法。

Deng等[29]研究了单闭环铰接桁架式可展开天线机构的构型综合问题，Xu等[30]基于螺旋理论研究了四面体构架式可展开天线机构的构型综合问题，Wang等[31]基于图论针对一类四棱锥式平面可展开天线机构进行了构型综合研究，文献[32]也利用图论理论针对可展开机构进行了构型综合研究。这些文献针对几类不同的可展开天线机构进行了构型综合的研究，但是目前关于环形桁架式可展开天线机构的构型综合的相关研究鲜有报道。

本文采用基于螺旋理论的约束综合法，针对环形桁架式可展开天线机构进行了构型综合研究，对环形桁架式可展开天线机构进行了收展原理分析并进行了结构分解，通过分析与综合得到了16种约束支链机构，并通过优选与组合得到了四种环形桁架可展开机构，最后针对综合得到的四种环形桁架机构在Solidworks软件中进行了三维建模与运动仿真，校验了各机构的可展性。本文的研究旨在为此类可展开天线机构的构型综合问题提供一种新思路，为后续的研究奠定基础，同时为其他类型空间可展开天线机构的构型分析与综合提供参考。

1 基于螺旋理论的约束综合法概述

根据螺旋理论[33]，空间一个螺旋可以用一个矢量来表示,写成矩阵的形式为：

(1)

式中：$表示螺旋，S为此螺旋轴线的方向，S0为直线的线距，r为螺旋轴线上任意一点在坐标系中的矢径，h为此螺旋的节距。

式(1)中的螺旋$可以表示一个刚体的运动或者作用在刚体上的一个力，分别称为运动螺旋和力螺旋。

当式(1)中h=0时，螺旋简化为线矢量，写成矩阵的形式为：

(2)

式(2)中的线矢量$可以表示转轴沿S方向的转动副(R)的运动螺旋，也可以表示为沿S方向，引起相对坐标系原点的力矩为r×S的纯力矢量。

当式(1)中h→∞时，螺旋简化为偶量，写成矩阵的形式为：

(3)

式中：0为3×1零矢量。

式(3)中$可以表示沿S方向的移动副(P)的运动螺旋，也可以表示轴线为S方向的纯力偶矢量。

其他类型的多自由度运动副可以用基本的单自由度转动副和移动副组合构成，如圆柱副(C)可以看成有一个转动副和一个移动副组合而成，球副(S)可以看成3个轴线相交但是不共面的转动副组合而成；空间的任意作用力也可以看成由纯力和纯力偶合成得到。

一个运动螺旋$r和一个约束力螺旋系$1,$2,$3,…,$n互为反螺旋的时满足如下螺旋互易积为0的关系：

$j∘$r=Sj·S0r+Sr·S0j=0(j=1, 2,…,n)

(4)

式中：“∘”表示螺旋的互易积计算符号。

当$1,$2,$3,…,$n表示并联机构中某一机构支链的运动螺旋系时，它们的反螺旋$r就表示该机构支链施加给动平台的约束力螺旋或约束力偶螺旋。动平台的约束螺旋系为所有机构支链施加给动平台的约束力螺旋或约束力偶螺旋的并集，它可以决定机构动平台的自由度，螺旋系的最大线性无关数等于机构动平台被约束掉的自由度数。

基于螺旋理论的约束综合就是根据机构约束与运动的对偶关系，采用螺旋描述和运算进行机构运动分析的逆过程，综合步骤通常为：先根据机构要求的运动输出构件的运动列写其运动螺旋系，并求出其所受约束螺旋系，如第2节内容所述；其次，构造支链约束螺旋并求出其相逆的基础运动螺旋系，如第3.1节前半部分内容计算与分析；再次，根据分支运动螺旋系构造分支运动链结构，如第3.1节后半部分内容分析与推导；最后，配置这些支链结构得到符合要求的机构，如第3.2节和第4节内容所述。

2 环形桁架可展开机构收展原理分析

环形桁架可展开机构是环形桁架式可展开天线的支撑骨架，如图1所示，其整体为空间多棱柱结构，由多个结构相同的单元机构连接而成，单元机构的投影为截面多边形的边，当边数增多时，整个多棱柱结构便更趋近于圆环形。

环形桁架机构可以分为上下环形边两部分，上层部分连接上层索网，下层部分连接下层索网，因此，对于环形桁架可展开机构进行构型综合时可以分别对上下环形边进行机构综合，然后连接上下环形边就可以得到整体环形桁架机构。

环形桁架机构的截面为平面多边形，设其顶点为A-F，中心位置处为O，多边形的每一条边即为一个单元机构的纵向截面形状，顶点处安装有节点花盘，收拢运动过程中各个单元机构收拢成一条空间直线，整体环形桁架收缩为较小体积的结构，反映在截面图中为多边形中各条边向环形中心运动，各条边的长度缩短，各个顶点相互靠拢。环形桁架截面形状及节点收拢运动过程如图2所示。

环形桁架截面为平面多边形，实现收拢时多个节点需要向多边形中心移动，每个节点和多边形中心之间可以采用一个P副来描述节点的运动特性，如图3所示。

3 环形边机构构型综合

3.1 环形边支链机构分析与综合

由第2节中的多边形节点收拢原理可知，图2和图3中的A-F节点花盘两两之间仅发生距离上的变化，且相邻节点之间移动收展方向不变，始终沿着初始位置两节点花盘连线方向，如图4所示。因此，可以在相邻两节点花盘之间添加能够实现沿着此方向移动的约束支链，使节点花盘能够跟随原来的运动，而且能在结构上限制两个节点花盘的相对运动。

根据收展时节点花盘的运动情况，假定各个节点均通过移动副向目标轴线收拢，在相邻两节点花盘之间添加约束支链后，约束支链与两个P副组成一个闭环，其可看成由两支链组成的并联机构，将与一个节点花盘连接的P副看成支链1，与另一个节点连接的P副和约束支链看成支链2。以图2～图4所示的节点花盘A和B为例，在两个节点花盘之间添加约束支链，如图5所示，根据节点花盘同步运动要求，该闭环机构应该只有一个自由度。

如图5所示，在节点花盘A(B)的最终收拢位置建立参考坐标系O-xyz，其中z轴沿目标收拢轴线，x轴沿支链1中P副的轴线，y轴由右手定则确定。则支链1中P副的运动螺旋在O-xyz中可表示为：

(5)

求式(5)中运动螺旋的反螺旋可得支链1施加给节点A的约束螺旋系为：

(6)

支链2由与节点花盘B连接的P副和添加的约束支链串联而成，为了使该两支链机构只有一个自由度，支链2的最大线性无关运动副数目应为6(若超过6则支链2存在局部自由度，说明节点B能独立运动)，且支链2提供的约束螺旋必须与式(6)所示的约束螺旋系线性相关，可以是式(6)中的五个约束螺旋中的0～5个。

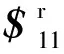
(7)

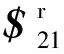
图7 提供两个约束力的约束支链机构
Fig.7 Constraint branch mechanisms which
can provide two constraint forces

图9 提供两个约束力和两个约束力偶的约束支链机构
Fig.9 Constraint branch mechanisms which can provide two
constraint forces and two constraint couples

图10 提供两个约束力和三个约束力偶的约束支链机构
Fig.10 The P joint which can provide two constraint
forces and three constraint couples

图13 提供一个约束力和三个约束力偶的约束支链机构
Fig.13 Constraint branch mechanisms which can provide a
constraint force and three constraint couples

根据以上分析可以得到十六种约束支链，支链提供的约束和机构构型汇总如表1所示。

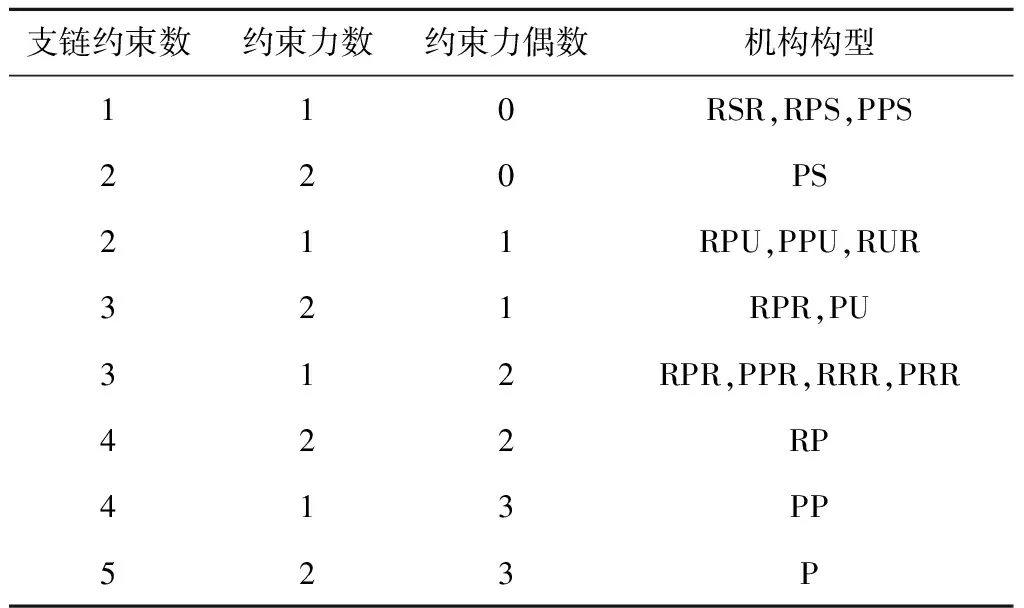
表1 支链约束和机构构型汇总表Table 1 Summary table of the branch constraint and mechanism configuration

3.2 环形边支链机构优选与环形边组合分析

环形桁架机构理想的收拢状态为收拢为一条空间直线，环形边上的节点花盘运动到重合位置，表1中所示的十六种约束支链均可以实现两个节点花盘间的相互运动，但是由于P副收拢率较低，若出现在个节点花盘的相对运动方向上会影响整体机构的收拢率，因此将在两个节点花盘连线方向上含有P副的支链去除，在其他方向上含有P副的支链可以保留，这样就得到了RSR,RUR,RRR和RRP支链机构，如图14所示。

进一步分析图14中的RSR，RUR和RRR支链，由于三个机构支链中所含的两端的转动副轴线均平行，机构支链两端的转动副会提供垂直于两端R副轴线方向的两个约束力偶，因此机构支链中的第三个运动副中的与两端转动副轴线不平行的转动会被约束掉，所以在两个节点花盘所处位置平面确定后RSR支链和RUR支链中的S副和U副中与两端R副不平行的转动会被约束掉，RSR支链和RUR支链的运动与RRR支链相同。由于RSR机构和RUR机构含有S副和U副等复合铰链，结构较为复杂同时会存在关节间隙较多的问题，因此在图14中所示的四个机构支链中，将RSR机构和RUR机构去除，选定RRR机构和RRP机构作为约束支链来构造环形桁架机构。

利用RRR机构和RRP机构来构造环形桁架机构，结合前述设定的各个节点花盘与中心点之间连线方向的移动副，以边数为6的多边形进行示意，得到的环形边机构如图15所示。

在环形边收展运动过程中，相邻两个节点花盘的靠近和远离会使得多边形的边长变短或者变长，此时会伴随有各个节点花盘靠近中心或者远离环形中心的被动运动过程，这与开始设置的各个节点花盘与中心点之间连线方向的移动副的作用相同，并且在两个节点花盘相互靠拢时可以不位于同一平面，最终收拢处于共线位置即可，因此可以将开始设置的各个节点花盘与中心点之间连线方向的移动副去除，只保留综合得到的环形边链路机构，如图16所示。

4 环形桁架机构综合

4.1 环形桁架整体机构综合与分析

在综合得到环形边链路机构之后，通过连接上下两个环形边链路机构便可以得到环形桁架机构，为保证上下环形边链路机构运动的同步性，可直接采用连杆连接处于同一竖向位置的节点花盘，进而得到环形桁架机构。第3节中分析综合得到的两个环形边链路机构，通过两个环形边链路机构的组合可以得到三种环形桁架机构，分别为基于RRR机构的环形桁架机构、基于RRP机构的环形桁架机构以及基于RRR+RRP机构的环形桁架机构，如图17所示。

图17中的三种环形桁架机构也可以看做是由6R机构单元、4R2P机构单元以及5R1P机构单元分别组成的环形桁架机构。

进一步针对图17中的图(a)所示的由RRR机构构成的环形桁架机构进行分析，此环形桁架机构可以看成是由多个6R机构单元组合而成，每个6R机构单元由两个RRR机构通过连杆连接组成，如图18所示。

图18中所示的6R机构单元在收拢时可以有三种不同的收拢折叠方式，三种收拢方式均可以实现两端节点花盘间的相互运动，如图19所示。

图19中所示的三种收拢方式中第二种收拢后的纵向包络尺寸较小，因此此类机构单元进行收展运动时，采用第二种收拢方式，同时图19中三种收拢方式中机构单元中间的两个转动副中心点在运动过程中始终处于同一条竖直线上，且图19中左侧的收拢方式中中间两个转动副之间的距离不变，始终与两侧连杆长度相同，因此可以在左侧收拢方式的中间转动副位置处添加节点花盘与连杆，将一个6R机构单元变为两个4R机构单元，如图20所示。

采用图20中所示的4R机构单元同样可以构造出环形桁架机构，如图21所示。美国的Astro-Mesh环形桁架天线正是采用的这种机构，这也是目前在轨应用较为成功的一种环形桁架天线机构。

同理可以分析图19中的另外两种收拢折叠方式，由于两种收拢折叠方式中机构单元的两个中间转动副在运动过程中距离不断变化，若要添加节点花盘与杆件则需在两个花盘之间添加P副，进而将上边(或下边)的3R机构转化为两个RRP机构，这与前面综合得到的机构链路相同，故不再对其进行分析。

至此，通过分析与综合，得到了图17以及图21所示的四种环形桁架可展开机构。

4.2 环形桁架机构建模与运动仿真

为了检验前述理论分析的正确性，针对前面综合优选得到的四种环形桁架可展开机构进行展开过程仿真校验，采用Solidworks软件进行三维建模，设置环形桁架机构单元边数为12，完全展开后单元边长设置为400 mm，展开后高度设置为600 mm，四种环形桁架机构完全展开后的外形轮廓相同，如图22所示。

虽然四种环形桁架机构完全展开后的外形轮廓相同，但是由于机构构型不同，其在完全收拢状态以及展开过程中的结构形态均不相同，在Solidworks软件中分别对综合得到的四种环形桁架机构添加驱动进行运动模拟，四种环形桁架机构的展开过程如图23所示。

经过运动仿真，图23中所示的四种环形桁架机构均以期望的收展运动完成了环形桁架机构的整体收展过程，校验了本文基于螺旋理论的环形桁架式可展开天线构型综合过程的正确性。

综合得到的几种环形桁架机构均可用于构造环形桁架式可展开天线，同时它们各有不同的特点，简单说明和概括如下：

1)基于4R机构单元和6R机构单元所组成的两种环形桁架机构中均只含有转动副，装配制造工艺性较好，在宇航空间环境中，转动副较移动副具有更好的运动灵活性。

2)在各个机构的节点花盘及杆件尺寸相当时，在完全收拢状态下，基于4R机构单元的环形桁架机构的收拢高度将大于其他三种机构，收拢状态下会占据更大的空间，但是相较于其他几种机构，此机构具有较少的铰链个数，因此关节累积间隙相对较小，整体结构刚度相对较高。

3)由于移动副需要在竖向连接杆上移动，基于5R1P机构单元和基于4R2P机构单元的两种环形桁架机构中，竖向连接杆的长度需要长于单元机构中横向连接杆的长度，才能保证整体机构可以完全收拢。

4)各个机构的节点花盘上两侧的转动铰链均需为同步铰链，从而确保整个环形桁架机构同步运动收拢与展开。

后续的工作将针对本文综合出的环形桁架机构进行进一步的特性分析与评价优选，并综合考虑工程实践需求进行优化与改进。

5 结 论

1)概述了基于螺旋理论的约束综合法，分析了环形桁架可展开天线机构的收展原理，将环形桁架机构分为了上下环形边两部分，可通过综合环形边机构并连接上下环形边得到环形桁架机构。

2)设置移动副来描述各个节点花盘的运动特性，采用基于螺旋理论的约束综合法针对环形边支链机构进行了分析与综合，得到了16种约束支链机构，并通过分析与优选得到了两种环形边支链机构，进而通过连接组合与推演得到了四种环形桁架可展开机构。

3)针对综合得到的四种环形桁架机构在Solidworks软件中进行了三维建模与运动仿真，校验了各机构的可展性，本文的研究为可展开天线机构的构型综合提供了一种新思路，综合得到的几种环形桁架机构可较好的应用于星载空间可展开天线领域。