线性自抗扰控制器的噪声抑制改进研究

张敏捷，杨 雷，侯砚泽，石 泳，左 光

(北京空间技术研制试验中心，北京 100094)

0 引 言

自抗扰控制技术继承和发扬传统PID控制的长处，借鉴和吸收现代控制理论先进成果，在过去三十年的发展过程中，既取得了丰富的理论研究成果，也在工程实践中获得了广泛应用。韩京清[1-2]在发展了非线性跟踪微分器、扩张状态观测器、非线性PID的基础上，系统提出了自抗扰控制器。Gao[3]引入带宽的概念将自抗扰控制器线性化，为自抗扰控制技术的系统化工程应用铺平了道路。Guo等[4-5]系统证明了自抗扰控制器的时域稳定性问题。孙明玮等[6-7]和杨瑞光等[8]深入研究了自抗扰控制器在飞行控制中的应用。赵坤等[9]针对再入弹头级联系统，设计扩张状态观测器对子系统各通道内的综合不确定性进行实时观测，并予以动态补偿，实现各通道的解耦控制。聂文明等[10]针对固体导弹助推段设计问题，采用扩张状态观测器实时估计系统建模误差与外部干扰，提出一类考虑质心运动与绕质心运动间的耦合作用的自抗扰制导控制一体化设计方法。杨茗棋等[11]针对基于电磁力的集群航天器构形维持控制问题，利用自抗扰控制器对集群航天器相对运动位置、速度进行实时估计，同时对模型不确定性和外部干扰进行估计和补偿，仿真表明其快速性和抗扰性都明显优于有限时间控制。

自抗扰控制的核心是扩张状态观测(Extended state observer，ESO)。提高扩张状态观测器的增益能提高ESO的收敛速度和估计能力，但高增益也会带来显著的噪声放大问题。实际工程中，传感器测量信号包含各种噪声污染，如果不加处理，轻则会引起控制器输出抖振，使得系统输出抖振，降低控制品质，减少执行机构的疲劳寿命；严重情况下，ESO高增益的噪声放大效应会削弱控制器稳定性，甚至引起控制器发散。尽管传感器测量信号一般都会经由扩展卡尔曼滤波(Extended Kalman filter，EKF)等方法进行滤波处理，但由于EKF采用了Taylor展开近似来处理系统模型非线性，一定程度上损失了滤波能力，导致滤波不够彻底，控制器所用滤波信号中仍会存在一定程度的噪声信号。如图1～3为采用LADRC进行姿态控制的小型固定翼无人机实飞数据。EKF滤波得到的俯仰角速度信号仍包含较大的噪声信号，引起LADRC控制器输出小幅抖振。

噪声污染问题是自抗扰控制器乃至一般控制器设计过程中必须予以考虑的问题。黄朝东等[12]分析了存在测量噪声时自抗扰控制器的工作能力，并通过频域分析方法定量给出：常值噪声主要影响ESO的一阶估计误差，高阶误差稳态值几乎不受影响；低频噪声对高阶稳态误差的影响小于对低阶稳态误差的影响；高频噪声对高阶稳态误差的影响大于对低阶稳态误差的影响。林飞等[13]研究了一阶滤波器对扩张状态观测器噪声抑制能力的改善作用。Lei等[14]通过仿真分析了船舶控制中Kalman滤波器、TD滤波器以及基于fal函数的滤波器对于LADRC控制器的滤波效果，但缺少对于不同滤波器滤波效果的对比仿真及理论分析。Cheng等[15]提出采用切换ESO增益的方法抑制噪声影响，仿真表明改进的ESO技能迅速估计系统状态同时有效抑制测量噪声。Patel等[16]研究了滑模观测器和自适应观测器两种非线性观测器对噪声的敏感性，研究结果表明尽管滑模观测器跟踪性能更好，但受噪声影响更大。Khalil及其学生[17-19]定量讨论了高增益观测器增益与噪声幅值对系统估计精度和控制精度的影响，并提出采用切换增益、非线性增益等方法来抑制噪声。以上研究没有考虑滤波延迟的问题，如果滤波延迟较大，尽管数值仿真中滤波效果不错，但实际应用中滤波带来的相位延迟却会降低系统闭环控制带宽，极易引起系统震荡甚至发散。在实际工程应用中，往往将扩张状态观测器的增益(带宽)限制在一个较小的值以下，避免观测器的噪声放大现象，从而保证系统的稳定性。这种保守设计一定程度上牺牲了ESO的收敛速度与估计能力，削弱了自抗扰控制器的抗干扰能力。

本文针对线性自抗扰控制器对高频噪声敏感的问题，设计了基于预报思想的跟踪微分器，提出了系统被噪声污染时的线性自抗扰控制器设计方法，为解决高增益带来的噪声污染问题，补偿滤波相位损失，增强自抗扰控制器的鲁棒性提供了新的思路。

1 线性自抗扰控制器

考虑一类具有单输入、单输出的非线性时变系统：

y(n)(t)=f(y(n-1)(t),…,y(t),w(t))+bu

(1)

式中:w(t)是外界扰动；b为控制增益；u为系统控制输入；y为系统输出；f(y(n-1)(t),…,y(t),w(t))表示被控对象动态，可以是时变、线性的，简记为f。记y=x1,y(k)=xk+1,k=1,2,…,n-1，并令xn+1=f。则系统动态特性式(1)可写为如下形式：

(2)

式中:xn+1称为扩张状态，它包括系统除控制输入外所有引起状态改变的作用，这一构造是自抗扰控制思想的核心。根据式(2)可构造如下包含扩张状态的Luenberger观测器，即扩张状态观测器：

(3)

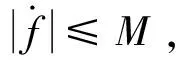
(4)

为Hurwitz矩阵，并使得状态观测器观测误差是有界的。利用ESO可以得到状态X=[x1,…,xn+1]T的估计值Z=[z1,…,zn+1]T，其中系统动态f的估计值为zn+1。利用zn+1，可将系统动态化为标准的串联积分器的形式：

(5)

y(n)=f+bu=f+bumain-zn+1≈bumain

(6)

特别对如下二阶系统：

(7)

要求系统状态x1跟踪指令信号xc。假定系统可测状态为x2，设计降阶扩张状态观测器：

(8)

适当选取ESO增益β1和β2，使得ESO状态变量[z1,z2]T逼近系统状态[x2,f]T。

进一步设计PD控制器：

uPD=kP(xc-x1)+kDx2

(9)

则

(10)

式(8)和式(10)即为二阶系统线性自抗扰控制器。式(7)～(10)构成的LADRC频域模型如图4所示。

2 噪声抑制自抗扰控制器设计

2.1 线性跟踪微分器

自抗扰控制器中跟踪微分器(Tracking differentiator，TD)被用来对输入控制器的指令信号进行平滑过渡。TD也具有较好的滤波作用。本文采用如下线性TD(Linear TD，LTD)[4]：

(11)

其中，v(t)为被噪声污染的参考信号;R和ai,(i=1,…,n)为相应的增益;[z1R(t),z2R(t),…,znR(t)]T为LTD状态变量，z1R(0)=z10,…,znR(0)=zn为其初值。文献[4]证明，当参考信号v(t)满足导数vk(t)(k=1,…,n)有界时，适当选取增益，使得

为Hurwitz矩阵，则任意给定LTD状态初值，当R→∞时，zkR(t)一致收敛于vk-1(t),k=1,…,n。

因此，二阶LTD为：

(12)

易得其传递函数为

(13)

2.2 预报跟踪微分器

在对被噪声污染的信号进行滤波时，滤波越彻底，信号的相位损失越严重。由于跟踪微分器不仅能输出参考信号的滤波值，还能同时给出参考信号的微分信号，因此本文提出利用微分信号对滤波信号进行适当的多步迭代“预报”，减少相位损失，即两步预测跟踪微分器(Predictor linear tracking differentiator，PLTD)：

(14)

第一步，根据滤波器前一步的微分信号，将滤波器前一步的输出信号向前预报k1步，然后将预报更新后的信号输入当前步跟踪微分器。

第二步，对当前步滤波器的输出信号，利用微分信号向前做k2步预测。

其中预报步数k1、k2的值可根据相位延迟大小利用仿真进行离线整定。

2.3 改进的LADRC

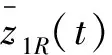
2.4 频域特性分析

由式(14)得PLTD的传递函数为：

(15)

从频域上理解:①预报即为在震荡环节中添加阻尼项;②预报为在此基础上叠加微分单元，补偿相位损失。

图6分别为惯性环节滤波器(时间常数T=1/50)、二阶LTD(a1=1,a2=1,R=50)和二阶PLTD(a1=1,a2=1,R=50,k1=10,k2=50,h=1/400)的伯德图。惯性环节和LTD在低频段就有较大的相位损失，而PLTD在低频段相位损失较小。

采用文献[7]提出的控制器疲劳度(Weariness degree，WD)，即控制器输出指令对传感器测量输入信号的传递函数)来评估控制器对噪声的鲁棒性。式(8)和(10)所述的二阶LADRC的控制器疲劳度为：

该系统虽然简单，但已经具备了新闻发布系统的基本功能。由于本人的能力和时间限制，在系统设计与制作过程中仍然存在诸多不足之处，如界面设计、系统功能、实用性等，都有待进一步完善。

(16)

利用PLTD改进后的二阶LADRC控制器疲劳度为：

GPWD=GWDGPLTD

(17)

3 仿真校验

本节以航空飞行器姿态控制问题为例，分析改进的LADRC的频域特性和时域特性。

3.1 频域特性

航空飞行器纵向短周期模态传递函数为

(18)

其中，q为飞行器俯仰角速度，δe为升降舵指令。给定a1=10.26,a2=124.16,a3=-91.83,a4=-278.17。根据式(8)和(10)设计LADRC控制器，其中β1=500,β2=2000,kP=-0.57,kD=0.08。分别选取惯性环节滤波器(时间常数T=1/50)、二阶LTD(a1=1,a2=1,R=50)和二阶PLTD(a1=1,a2=1,R=50,k1=10,k2=100)，利用式(17)得到对应的LADRC控制器疲劳度如图7所示，对应LADRC闭环伯德图如图8所示。由图7可看出，在高频段，不同滤波器均能减小信号的幅值，抑制噪声的影响，增强LADRC对于噪声的鲁棒性。由图8可看出，在低频段，不同滤波器对LADRC的闭环频率特性影响较小；在中频段，PLTD相比其他滤波器，能有效弥补LADRC闭环控制相位损失。

3.2 时域仿真

对改进的LADRC进行硬件在环仿真(Hardware in the loop test，HIL)。HIL仿真平台包括实时动力学仿真机、飞控计算机、交换机、地面站、视景计算机、遥控器等，如图9所示。为了模拟真实情况下的噪声污染，在仿真模型的角速度输出信号中叠加了白噪声。

3.2.1未滤波

3.2.2惯性滤波器

离散惯性滤波算法如下：

y0(k+1)=y0(k)-hα(y0(k)-v)

(19)

其中，α为惯性滤波器滤波因子。分别取α为50和200，HIL仿真结果如图13所示。

可以看到惯性滤波器未能有效滤除噪声，效果不甚理想。

3.2.3二阶LTD滤波

采用(11)式给出的二阶LTD，其中，参数按照标准二阶震荡环节配置为：R=30,a1=1,a2=2，HIL仿真结果如下：

由图14可看到，由于传统LTD滤波带来的延迟较大，导致LADRC控制器闭环特性变慢，削弱了LADRC控制器的稳定性，引起系统状态变量的震荡。

3.2.4PLTD滤波

采用式(14)给出的滤波算法，其中，R=30,a1=1,a2=2,k1=10,k2=100，HIL仿真结果如图15～16所示。

由图15可以看出，PLTD有效滤除了俯仰角速度测量值中的高频噪声部分；从图16可以看出，基于PLTD的改进的LADRC相位损失较小，俯仰角的闭环特性变化不大；从图17可看出改进的LADRC输出的控制指令平滑，受噪声污染影响较小。基于PLTD的改进的LADRC，既能有效抑制高频噪声污染，又能降低滤波带来的控制器闭环相位延迟，从而提高了LADRC控制器对于高频噪声的鲁棒性，提高了LADRC的控制性能，保证了LADRC控制器的闭环稳定性。

4 结 论

本文针对系统输出被噪声污染控制器设计问题，设计了一种基于预报线性跟踪微分器的自抗扰控制器。仿真结果表明，相比惯性滤波器和一般线性跟踪微分器，该方法能抑制噪声污染对系统闭环特性的影响，并能有效抑制滤波带来的相位延迟现象，降低高增益观测器带来的噪声污染放大问题，增强控制器的鲁棒性。该方法增强了线性自抗扰控制器对于高频噪声的鲁棒性，具有工程实用性。为调参便利，本文中预报参数k1和k2取为整数，事实上也可灵活取为小数。如何综合考虑自抗扰闭环特性以及传感器噪声特点，平衡滤波效果与闭环相位损失，选取较优甚至最优的预报参数，是值得研究的问题。未来的研究可在预测跟踪微分器调参及非线性预报跟踪微分器等方面做进一步的工作。