广义空间调制中的高效天线选择算法

祁婷 田红心 杜文丛 方旭愿

摘  要： 天线选择技术是一种能够提供高分集增益的有效手段。广义空间调制（GSM）系统可以与天线选择相结合使BER性能和系统容量得到提升。文中首先研究了GSM系统中基于欧氏距离的天线选择算法;然后提出一种低复杂度的基于模值排序准则的天线选择算法;为了取得复杂度和传输性能的折中，最后提出一种结合模值排序和欧氏距离的天线选择算法。仿真分析结果表明，提出的新型结合模值排序和欧氏距离的算法是一种更有效的系统优化算法。

关键词： 广义空间调制; 天线选择; 多输入多输出技术; 欧氏距离; 信息传输; 模值排序准则

中图分类号： TN925?34                          文献标识码： A                         文章编号： 1004?373X（2019）15?0021?04

Efficient antenna selection algorithm used in generalized spatial modulation

QI Ting1， 2， TIAN Hongxin1， DU Wencong1， FANG Xuyuan1

（1. School of Telecommunications Engineering， XIDIAN University， Xian 710071， China;

2. Department of Command Information Systems and Networks， Air?force Communication NCO Academy， Dalian 116600， China）

Abstract： Antenna selection technique is an effective means to provide high diversity gain. The generalized spatial modulation （GSM） systems can be combined with antenna selection to improve BER performance and system capacity. The antenna selection algorithm based on Euclidean distance in GSM system is studied in this paper， and then a low?complexity antenna selection algorithm based on modulus?sorting criterion is proposed. In order to achieve the trade?off between complexity and performance， an antenna selection algorithm combining modulus sorting and Euclidean distance is proposed. The simulation results show that the new algorithm combining modular value sorting and Euclidean distance is a more effective system optimization algorithm.

Keywords： generalized spatial modulation; antenna selection; multi?input multi?output technology; Euclidean distance; information transmission; modulus?sorting criterion

0  引  言

多输入多输出（Multiple Input Multiple Output，MIMO）技术因为其能够成倍地提高系统传输速率且不需要增加额外的带宽而成为未来移动通信系统的核心技术之一[1]。特别地，大规模的MIMO系统的发射天线和接收天线数目远高于传统的MIMO系统，从而可以成倍地提升传输性能和通信容量。然而，随着天线数量的大幅度增长，传统MIMO技术空时分组码（Space?Time Block Code，STBC）和垂直分层空时码（Vertical?Bell Laboratories Layered Space?Time，V?BLAST）需要庞大的射频链路数量，这将消耗更多的成本[2?3]。此外，随着收发天线数量的增加，STBC和V?BLAST的空间信道数量将显著增长，若对每条信道进行信道估计和时频同步将消耗巨大的系统资源。随着天线数量的增长，接收端检测的复杂度呈指数级增长。因此，设计新型、能够兼顾容量优势和突破传统限制的MIMO传输方案是无线通信领域的热点研究方向。

广义空间调制（Generalized Spatial Modulation，GSM）作为一种全新的MIMO传输技术被提出[4?7]。相比传统MIMO，其特征在于，在每个时隙利用被激活的多根天线索引，即空间维度携带的信息，对激活天线进行幅度相位调制[8?9]。GSM在保持传输效率和性能的同时，能够降低MIMO系统的复杂度和硬件开销。相比传统MIMO，利用GSM的MIMO系统在信号传输过程中仅激活少量发射天线，从而系统的发射端仅需要少量的射频链路用于传输，这种简化结构有利于降低大规模MIMO系统成本。天线选择技术是一种能够提供高分集增益的有效手段。GSM系统的检测方法大体上分为两大类[10?12]，即天线序号判定与星座映射独立进行和天线序号与星座联合检测。研究证明，联合检测算法具有更好的性能[13?16]。

本文着眼于系统性能和实现复杂度，结合GSM和天线选择，首先，基于最小欧氏距离最大化准则，提出GSM系统中的最优天线选择算法;然后，分析得出最优天线选择算法需要遍历所有可能的发射符号，具有较高的复杂度的结论。在此基础上为了降低系统复杂度，提出一种基于模值排序的算法，即取发射天线对应的信道列向量模值较大的几列发射天线作为选择的发射天线;最后，还提出一种结合模值排序和欧氏距离的算法，即先利用模值排序得到一个较小的备选天线集合，然后在备选天线集合里利用最小欧氏距离最大化选择天线。

1  系统模型

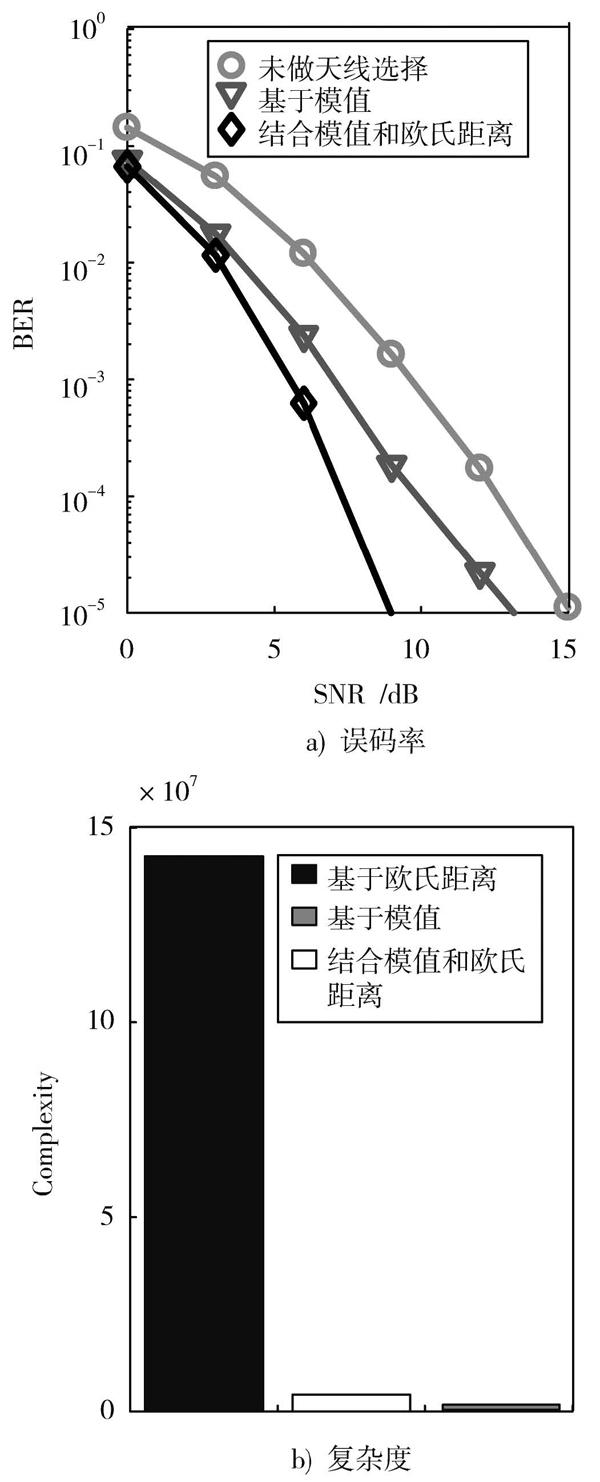
考虑一个有[Nt]根发射天线和[Nr]根接收天线的广义空间调制系统。天线选择是从[Nt]根发射天线中自适应地选择[nt]根进行数据传输。在发射端，[P]（[P

式中：[Ik=（k1，k2，…，kP）∈II]，表示激活的天线组合;调制符号[sk=sk1，sk2，…，skPT∈S]，是激活天线上對应的星座符号，[S]表示所有[P]维的星座符号的集合。

假设发射天线和接收天线通过频率选择性慢衰落信道进行通信，信道矩阵为[H=[h1，h2，…，hNt]∈C?Nr×Nt]，其服从复高斯分布[CN（0，1）]。令[IAS=linti=1]表示备选天线集合，其中天线[li]来自集合[T=1，2，…，Nt]。[HIAS=hl1，hl2，…，hlnt]表示实际选择的天线和接收天线之间的信道矩阵。令[Δ]表示所有[CntNt]种可能的天线组合的集合。

因此，接收信号[Y∈C?Nr×1]可以表示为：

式中：[n∈C?nt×1]表示随机复噪声向量，服从分布[CN（0，σ2）]。

2  广义空间调制系统中天线选择设计准则

2.1  基于最小欧氏距离最大化准则的天线选择算法

定义发射符号经过信道得到的接收信号的差值[dmin]的2范数为：

通过最小化[dmin]，可以最小化条件成对错误概率。因此[dmin]可以作为选择最优天线组合的决策指标。这样广义空间调制系统的天线选择设计标准为：

2.2  基于模值排序准则的天线选择算法

上述天线选择算法虽然有最优的性能，但其需要遍历所有可能的发射符号，具有较高的复杂度。为了降低复杂度，本节提出一种基于模值排序的天线选择算法。具体过程如下，计算信道矩阵[H]的[Nt]列的模值如下所示：

2.3  结合模值和距离的新型天线选择算法

上述基于模值排序准则的天线选择算法虽然易于实现，复杂度低，但它的性能不太好。为了进一步提升性能，下面给出一种结合模值排序和欧氏距离的天线选择算法。具体过程如下：先通过模值排序得到[H]模值排序[k=[k1，k2，…，kNt]]，如式（6）所示，然后取[k]的前[nt+m]个值作为备选天线集合：

2.4  复杂度分析

下面分析基于最小欧氏距离最大化准则、基于模值排序准则和基于结合模值排序和欧氏距离准则三种天线选择算法的复杂度。本文使用flop数来度量三种算法的复杂度。一个flop表示一次实数乘法或加法运算。

基于最小欧氏距离最大化准则天线选择算法的复杂度为：

3  仿真分析

下面比较广义空间调制系统中基于最小欧氏距离最大化准则、基于模值排序准则以及结合模值排序和欧氏距离三种天线选择算法的性能。仿真中假设在接收端已知理想的信道状态信息。

图1表示在不同信噪比下，三种检测算法的误码率（Bit Error Rate，BER）和复杂度。仿真条件是发射天线数目[Nt=6]，选择的天线数目[nt=4]，激活天线数目[P=2]。接收天线数目[Nr=4]，控制备选集合大小参数[m=1]。从仿真结果可以看出，基于最小欧氏距离最大化准则算法有最好的性能，但它的算法复杂度也是最高的。结合模值和欧氏距离的算法拥有与基于欧氏距离算法相似的性能，并且它的复杂度只有基于欧氏距离的[13]。另一方面，结合模值和欧氏距离的算法性能比基于模值算法的性能好。

图2的仿真参数是发射天线数目[Nt=12]，选择的天线数目[nt=4]，激活天线数目[P=2]，控制备选集合大小参数[m=2]。接收天线数目[Nr=4]，仿真结果与图1的类似。由图2可以看出，本文所提出的新的结合模值排序和欧氏距离的天线选择算法可以在计算复杂度和传输性能之间取得更好的折中，因此是一种更高效的系统优化算法。

4  结  语

本文提出广义空间调制系统中基于最小欧氏距离最大化准则、基于模值排序准则以及结合模值排序和欧氏距离混合准则的三种天线选择算法，并通过理论分析和计算机仿真比较它们的性能和复杂度。经过仿真结果表明，所提出的新型混合准则算法能够在计算复杂度和性能之间取得更好的折中，是一种更具有应用价值的新型天线选择算法。

图1  6选4的情况下三种检测算法的误码率和复杂度

图2  12选4的情况下三种检测算法的误码率和复杂度

参考文献

[1] NGO H Q， LARSSON E G， MARZETTA T L. Energy and spectral efficiency of very large multiuser MIMO systems [J]. IEEE transactions on communications， 2015， 11（2）： 87?105.

[2] ALAMOUTI S M. A simple transmit diversity technique for wireless communications [J]. IEEE journal on selected areas in communications， 1998， 16（8）： 1451?1458.

[3] WANG J， JIA S， SONG J. Generalised spatial modulation with multiple active transmit antennas and low complexity detection scheme [J]. IEEE transactions on wireless communications， 2012， 11（4）： 1605?1615.

[4] DI RENZO M， HAAS H， GHRAYEB A， et al. Spatial modulation for generalized MIMO： challenges， opportunities and implementation [J]. IEEE proceedings， 2014， 102（1）： 56?103.

[5] YANG P， RENZO M D， HANZO L， et al. Single?carrier SM?MIMO： a promising design for broadband large?scale antenna systems [J]. IEEE communications surveys tutorials， 2016， 18（3）： 1687?1716.

[6] ZHANG J， WANG Y， DING L， et al. Bit error probability of spatial modulation over measured indoor channel [J]. IEEE tran?saction on wireless communications， 2014， 13（3）： 1380?1387.

[7] WANG S C， LI Y Z， WANG J， et al. Low complexity multiuser detection in massive spatial modulation MIMO [C]// Procee?dings of 2014 IEEE Globecom Workshop. Austin： IEEE， 2014： 784?789.

[8] NARASIMHAN T L， RAVITEJA P， CHOCKALINGAM A. Generalized spatial modulation in large?scale multiuser MIMO system [J]. IEEE transactions on wireless communications， 2015， 14（7）： 3764?3799.

[9] BASAR E. Multiple?input multiple?output OFDM with index modulation [J]. IEEE signal processing letters， 2015， 22（13）： 2259?2263.

[10] FAN R， YU Y J， GUAN Y L. Generalization of OFDM with index modulation [J]. IEEE transactions on wireless communication， 2015， 14（10）： 5350?5359.

[11] BASAR E. On multiple?input multi?output OFDM with index modulation for next generation wireless networks [J]. IEEE transactions on signal processing， 2016， 64（15）： 3868?3878.

[12] TANG Q， XIAO Y， YANG P， et al. A new low?complexity near?ML detection algorithm for spatial modulation [J]. IEEE wireless communications letters， 2013， 2（1）： 90?93.

[13] MEN H， JIN M. A low?complexity ML detection algorithm for spatial modulation system with PSK constellation [J]. IEEE communications letters， 2014， 18（8）： 1375?1378.

[14] ZHANG W， YIN Q， DENG H. Differential full diversity spatial modulation and its performance analysis with two transmit antennas [J]. IEEE communications letters， 2015， 19（4）： 677?680.

[15] XIAO L， YANG P. A low?complexity detection scheme for differential spatial modulation [J]. IEEE communications letters， 2015， 19（9）： 1516?1519.

[16] RAJASHEKAR R， ISHIKAWA N， SUGIURA S， et al. Full?diversity dispersion matrices from algebraic field extensions for differential spatial modulation [J]. IEEE transactions on vehicular technology， 2016， 66（1）： 385?394.